The pathophysiological basis of schizophrenia remains largely unknown. One promising research tool is computer modelling, which has become central to a range of other disciplines that examine complex systems. The usefulness of a good model is not to emulate the full details of reality, but to elucidate conceptual relationships between phenomena that previously seemed unrelated and to yield new, testable predictions. Along these lines, computer models of large arrays of interacting neural elements have been used to explore normal and pathological brain processes (e.g. Reference Grunze, Rainnie and HasselmoGrunze et al, 1996). In this spirit, we describe a computer model of a neural network that organises stored information into categories. It is a useful model because it delineates a conceptual link between cognitive studies of patients with schizophrenia demonstrating enhanced semantic priming and post-mortem studies suggesting reduced corticocortical connectivity in the brains of such patients.
Semantic priming and schizophrenia
It has often been observed that people with schizophrenia seem to get ‘stuck’ in semantic categories. Bleuler gives as an example the patient who gave as her family members ‘father, son… and Holy Ghost’. The experimental analogue of this is semantic priming. An early study by Meyer & Schvaneveldt (Reference Meyer and Schvaneveldt1971) demonstrated that when normal subjects were shown a target word (e.g. ‘nurse’) they could more quickly identify it (as a word v. a non-word) when it was preceded by a semantically related priming word, such as ‘doctor’, as opposed to an unrelated word, such as ‘bread’. This effect was termed ‘semantic priming’. Maher (Reference Maher, Maher and Maher1983) proposed that associative intrusions expressed in the speech of patients with schizophrenia arise, at least in part, from enhanced semantic priming. Subsequent studies have tended to support this view. Studies by Manschreck et al (Reference Manschreck, Maher and Milavetz1988), Spitzer et al (Reference Spitzer, Weisker and Winter1994), Henik et al (Reference Henik, Nissimov and Priel1995) and Kwapil et al (Reference Kwapil, Hegley and Chapman1990), among others, all showed greater semantic priming in patients with schizophrenia relative to a normal control group.
It should be noted that some more recent studies (e.g. Reference Barch, Cohen and Servan-SchreiberBarch et al, 1996) have not demonstrated enhanced semantic priming in patients with schizophrenia. One explanation for these discrepant findings is suggested by Maher et al (Reference Maher, Manschreck and Redmond1996), who showed that semantic priming was positive for patients with short length of illness, but declined to negative values as the length of illness increased. The gradient of decline was significant and was shown to be neither an artefact of age nor related to medication status. They concluded that the probability of positive semantic priming among people with schizophrenia depends significantly on chronicity of illness. Consistent with this view is a body of research indicating that later stages of schizophrenic illness are associated with cognitive slowing (e.g. Reference Mitrushina, Abara and BlumenfeldMitrushina et al, 1996), which will increase reaction time and contaminate semantic priming estimates. Significantly, studies that have called into question enhanced priming in schizophrenia have not taken into account length of illness. A second explanation is suggested by studies demonstrating that the subgroup of thought-disordered patients with schizophrenia show heightened semantic priming (Reference Maher, Manschreck, Hoover, Harvey and WalkerMaher et al, 1987; Reference Manschreck, Maher and MilavetzManschreck et al, 1988; Reference Spitzer, Weisker and WinterSpitzer et al, 1994). Similarly, Moritz et al (Reference Moritz, Andresen and Domin1999) demonstrated that people who were not diagnosed with any psychiatric disorder but revealed schizophrenia-like language disturbances showed increased priming. Therefore, studies focusing on patients with more recent onset and with thought disorder seem especially likely to demonstrate enhanced semantic priming.
A third issue is the operationalisation of priming measures. Priming is generally measured in one of two ways: a word pronunciation test or a lexical decision task. Spitzer has argued that the lexical decision method is most appropriate, as the naming required for the word pronunciation task can be performed by participants without semantic processing (M. Spitzer, 1999, personal communication). This matter is significant because some of the negative studies (including that of Reference Barch, Cohen and Servan-SchreiberBarchet al, 1996) employed the word pronunciation task. The above considerations, taken together, suggest that excessive semantic priming remains an important clinical phenomenon in understanding neurocognitive alterations in a significant subgroup of patients with schizophrenia.
Theoretical explanations: spreading activation
Most models of semantic priming have largely relied on notions of ‘spreading activation’. This approach assumes that individual neurons or small groups of neurons code for particular concepts — a theory of local representation. Researchers who have used this framework to explain semantic priming envisage semantic information as organised in ‘webs of meaning’, in which nodes coding for similar concepts are closer together and more strongly connected than those coding for dissimilar concepts. When a concept (node) is activated, this activation spreads to its neighbouring nodes and decays over time, so that more distant, and semantically unrelated, concepts are not activated (see Reference Collins and LoftusCollins & Loftus, 1975).
There is scant neurobiological evidence, however, that the brain relies on localised representation to store and retrieve memories. This view forces the conclusion that each concept is required to have its own unique set of neurons — there would need to be specific neurons corresponding, for instance, to ‘grandmothers’. Rather, there is instead a large and growing body of theoretical and empirical studies indicating that the brain stores and processes information as distributed patterns of activation (Reference BresslerBressler, 1995). If so, neurobiological mechanisms of semantic priming require another explanation.
Neurodevelopmental models of schizophrenia
It is well known that adolescence is accompanied by dramatic reductions in corticocortical connectivity in frontal regions and probably other regions of human association cortex (Reference HuttenlocherHuttenlocher, 1979). Some workers have proposed that schizophrenia arises from excessive loss of corticocortical connectivity (e.g. Reference FeinbergFeinberg, 1982; Reference Hoffman and McGlashanHoffman & McGlashan, 1997). Consistent with that view are studies demonstrating reductions in cortical neuropil (Reference Selemon, Rajowska and Goldman-RakicSelemonet al, 1995), synapse-associated phosphoproteins (Reference Eastwood and HarrisonEastwood & Harrison, 1995) and dendritic spine density (Reference Glantz and LewisGlantz & Lewis, 2000) in patients with schizophrenia compared with normal controls. Given that schizophrenia generally emerges during late adolescence or early adulthood, these data suggest that this disorder may represent a failure to arrest the normal, physiological process of pruning of connections during adolescence.
The study reported below uses a distributed model of neural network processes to investigate effects of reduced corticocortical connectivity on semantic priming. Our model used two network modules: one specifying semantic categories, and a second module characterising items within categories. Neurons exchanged connections within and between each of the two modules. We predicted that reductions in connectivity within the modules would enhance the salience of semantic category information transmittedbetween the modules. If so, excessive reductions in within-module connectivity would lead to excessive semantic priming. The relevance of this approach is suggested by a study by Woo et al (Reference Woo, Pucak and Kye1997) demonstrating in monkeys that frontal pruning occurring around pubescence selectively reduces local rather than distant connections. Viewing schizophrenia as a pathological extension of late (i.e. adolescent) cortical pruning therefore suggests that local connections are preferentially lost in this disorder, thereby leading to excessive semantic priming.
METHOD
Basic network
This study employed a modified 120-neuron Hopfield network. It was based on prior network simulations described by Hoffman & Dobscha (Reference Hoffman and Dobscha1989) and Meilijson & Ruppin (Reference Meilijson and Ruppin1992). Other examples of the application of this modelling methodology to psychiatric problems can be found in reports by Carrie (Reference Carrie1993) and Ruppin & Reggia (Reference Ruppin and Reggia1995). A concise introduction to the field of neural network modelling more generally has been given by Hinton (Reference Hinton1992).
At any given time, each neuron in the system is either active or inactive, these states being represented by neuronal activations of 1 and 0, respectively. Thus, at any instant, the state of the network can be characterised by a 120-dimensional binary vector. During one cycle, or iteration, the state of the network is updated using the following two-step process.
First, all inputs to a given neuron, both intrinsic and extrinsic, are summed and a threshold function is applied. Input to neuron μ j is calculated by multiplying the axonal output of each neuron supplying input into it (termed si below) by the i→j connection weight, termed Tij . That is,
If this sum is greater than a preset threshold, the neuron is activated; otherwise, it is inactivated. Our threshold was 0.048=p × (1 -p) × (1 — 2p)/2 (Reference Horn, Ruppin and UsherHorn et al, 1993), where p is the average level of activation of the stored memories.
Next, in order to capture the fluid, dynamic nature of neurocognitive processes, an adaptation factor was included to allow our simulation to shift readily from one attractor to another. We chose to model adaptation by degrading neuronal output in an activity-dependent manner. That is, each time a neuron is activated, the strength of its axonal signal is diminished; if and when the activation of the neuron falls to 0, the adaptation level is reset to 0. Mathematically, we can represent this by the following set of difference equations:
under the conditions
and
The expression si (t) is the axonal output of neuron i at time t, and xi (t) can be thought of as a measure of the degree to which adaptation ‘accumulates’ for a given neuron. This output,si , which varies from 0 to 1, then produces inputs to the other neurons of the system, as described above. The parameters b andf jointly embody the adaptation characteristics and define the shape of the adaptation curve; our simulations used b=7 and f=1.2. Other workers have described similar but distinct methods for simulating neural adaptation (e.g. Reference Meilijson and RuppinMeilijson & Ruppin, 1992).
Memory storage and retrieval
Each of the network's ‘memories’ was a particular pattern of activation of its 120 constituent neurons and, as such, each could be represented by a 120-element binary vector. Memories were created in which, on average, only 20% of the constituent neurons were active; thus, a typical memory was composed of approximately 24 (randomly selected) active neurons. The network was trained by presenting a given memory — that is, turning on the neurons of the network corresponding to the activated neurons of the memory. The formula below was then applied, which increased the connection weight between any two neurons that are activated simultaneously (Reference Amit, Gutfreund and SompolinskyAmit et al, 1987); this serves to embed memories and the categories to which they belong in the network connection strengths:
where zs is the level of activation of memory s. Level of activation for a given memory is defined by:
A similar set of connections could have been obtained by presenting the stimuli in a training context using a ‘classical’ Hebbian learning scheme.
Simulation of cognitive priming
Testing cognitive priming in a neural network system requires patterns of neuronal activation (memories) of different categories. We operationalised this as follows. The first 40 of the memory's 120 neurons were designated as ‘categorical’. For a given category, the activation states of these 40 neurons were randomly generated and identical for all memories of that category. The remaining 80 neurons — designated as ‘case’ neurons — were generated randomly for all memories in all categories. Twenty-five memories, five in each of five categories designated A to E, were generated.
To test cognitive priming, the system was presented with a particular memory, say memory 1 from category A. The network then cycled through five iterations. For each cycle, adaptation was applied to neuronal outputs, and the network's new activation state was calculated as described above. After this ‘exposure’ phase, a different memory from the same category (say, memory 2 of category A) was presented to this primed network. However, this memory was presented in a highly degraded form: only 33% of the nodes constituting the memory, which were selected randomly by the program, were presented. The network then returned a pattern of activation which might or might not resemble that of memory 2.
At this point the network's performance — that is, how readily it could identify the degraded stimulus — was tested. To do this, the 120 units of the network's output were compared with the 120 units of a given memory vector. The sum of the instances in which corresponding elements were both 1 was calculated and divided by the number of active neurons in the memory in question. This was repeated for each of the 25 memories. We termed this quotient the ‘similarity quotient’ and used it to rank the memories, the highest being most similar to the network's output. If this was the same as the cued memory (in our example, memory 2) and its similarity quotient, as defined above, was 0.4 or greater, it was counted as a ‘correct hit’. If these two criteria were not met, it was scored as an incorrect response. All 25 memories were used as both priming and test patterns, and the above procedure was carried out for all 125 intracategory prime—test combinations.
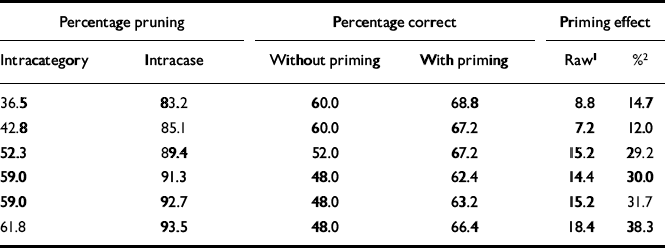
We evaluated the priming effect by first calculating the number of correct hits achieved under priming (0-125) and dividing by 125; this figure is shown in column 4 of Table 1. To evaluate the base-line (unprimed) performance of the system, each of the 25 patterns was degraded to 33% of its original activation, as it had been in the test scenarios, and presented to the system; the percentage of times the network could identify the test pattern was calculated (column 3 of Table 1).
Table 1 Change in priming performance of network in response to increased pruning
| Percentage pruning | Percentage correct | Priming effect | |||
|---|---|---|---|---|---|
| Intracategory | Intracase | Without priming | With priming | Raw1 | %2 |
| 36.5 | 83.2 | 60.0 | 68.8 | 8.8 | 14.7 |
| 42.8 | 85.1 | 60.0 | 67.2 | 7.2 | 12.0 |
| 52.3 | 89.4 | 52.0 | 67.2 | 15.2 | 29.2 |
| 59.0 | 91.3 | 48.0 | 62.4 | 14.4 | 30.0 |
| 59.0 | 92.7 | 48.0 | 63.2 | 15.2 | 31.7 |
| 61.8 | 93.5 | 48.0 | 66.4 | 18.4 | 38.3 |
Comparison with clinical data
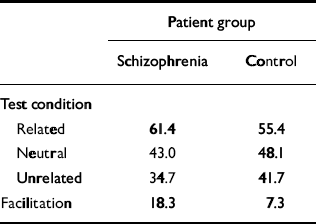
Performance of our computer model was compared with an empirical study of priming in schizophrenia reported by Kwapil et al (Reference Kwapil, Hegley and Chapman1990). These researchers created a pool of 96 semantically related word pairs (i.e. 96 prime—target combinations). First, the priming word was displayed to the person undergoing the test, then a blank screen was shown briefly, then the degraded target word was displayed. To establish a baseline, or non-primed, condition, the word ‘blank’ was shown as the prime. For the ‘unrelated’ condition, prime and target words were of different semantic categories. The percentage of correctly identified words was recorded; the overall results are summarised in Table 2. Their ‘percentage correct in the neutral condition’ is analogous to our measure of percentage correct without priming. Similarly, their ‘related’ test condition is analogous to our percentage correct with priming. Participants with schizophrenia showed a clear positive priming effect when compared with a control group, as well as in a comparison with patients with bipolar affective disorder.
Table 2 Comparison of clinical findings and network results. Summary of semantic priming data from the study by Kwapil et al (Reference Kwapil, Hegley and Chapman1990)
| Patient group | ||
|---|---|---|
| Schizophrenia | Control | |
| Test condition | ||
| Related | 61.4 | 55.4 |
| Neutral | 43.0 | 48.1 |
| Unrelated | 34.7 | 41.7 |
| Facilitation | 18.3 | 7.3 |
Neural pruning
Our simulation differentiated between category regions and case nodes, the former comprising a subset of 40 ‘neurons’ and the latter 80 ‘neurons’. This assignation allowed us to distinguish three sorts of connections: those restricted to category neurons (intra-category connections), those restricted to case neurons (intracase connections), and those that connected case and category neurons. To make this explicit we have represented the two sets of ‘neurons’ as anatomically segregated in Fig. 1, but clearly this does not imply that they are segregated in real nervous systems.

Fig. 1 Neural pruning. The shaded upper rectangles represent intracategory neurons and their connections; the larger squares below represent non-categorical (case) neurons. The left-hand diagram represents the baseline (normal) condition. The right-hand diagram represents schizophrenia — there is increased intracategory and intracase pruning, and a greater importance of case—category connections.
Connectivity was reduced using a ‘pruning parameter’ for each category of connection: if the absolute value of an axon's weight factor was below this threshold, it was eliminated (i.e. set to 0). We used one pruning parameter for both intracategory and intracase connections (hereafter referred to as intramodular connections) and a second pruning parameter for between-module connections.
RESULTS
The system was initially optimised so that it quantitatively simulated priming behaviour in the normal subjects in the study by Kwapil et al (Reference Kwapil, Hegley and Chapman1990). The intramodular pruning parameter was set at 0.0106 and the intermodular pruning parameter at 0.007. These parameters produced intra-category, intracase and category—case pruning levels of 36.5%, 83.2% and 64.7%, respectively. The network produced the correct memory — that is, the one that was cued for — 68.8% of the time when it was primed in that category. In contrast, it achieved a success rate of 60% without priming. These data correspond to a priming effect of 14.7%, that is (68.8-60)/60. This percentage is very close to the priming effect of 15.2% obtained by Kwapil et al, which was computed by subtracting the percentage correct under the neutral condition from that for the related condition, as shown in Table 2, and dividing by that for the neutral condition. Figure 2 demonstrates the dynamic behaviour of the network in response to primed and unprimed inputs using these parameters.
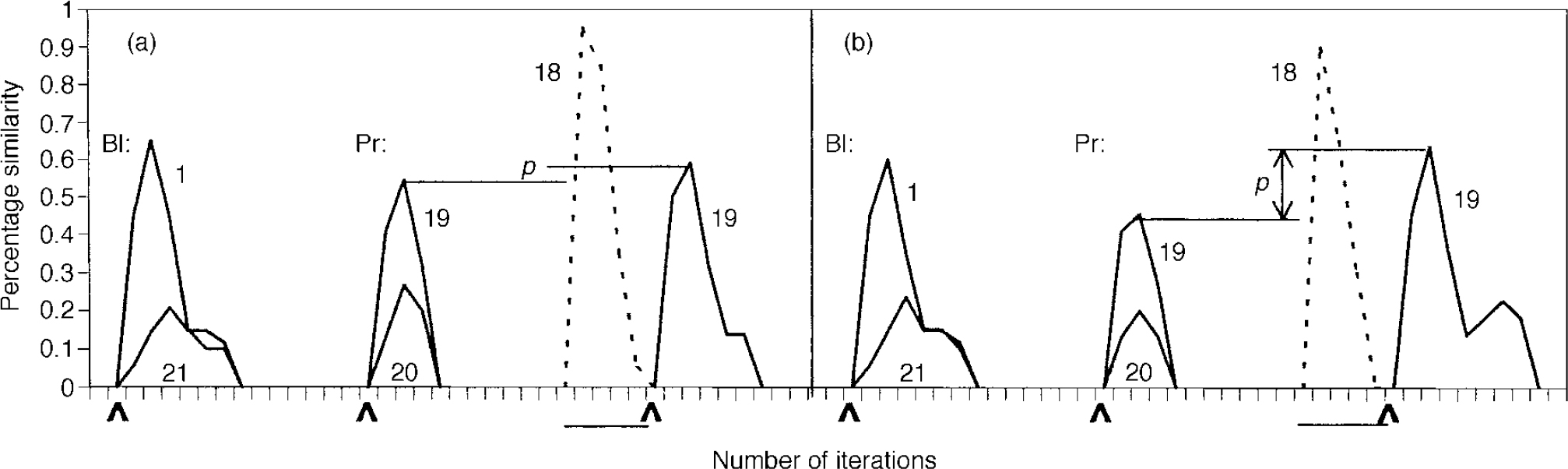
Fig. 2 Dynamic behaviour of the network in the normal (a) and schizophrenic (b) conditions. Baseline (BI) condition: 0.33 of memory pattern is presented at the point indicated by the arrow; network activation is shown. Activation of a typical out-of-category pattern, 21, is presented for comparison. Note the lower level of activation in the schizophrenia case compared with the normal case (0.6 v. 0.65). Priming (Pr) behaviour: pattern 19 is presented at 0.33 to indicate baseline performance; pattern 20's activation is shown for comparison. The system is next primed with an in-category memory (18) at 0.85, as indicated by the horizontal bar; activation is shown in dotted outline. Pattern 19 is then presented at the point indicated by the arrow. This figure is presented to give a feel for the functioning of the system over time. Priming is qualitatively indicated by distance p; note its increased level in the schizophrenic condition. The quantitative method of calculating priming is based on percentage correct performance, as described in the text.
By varying one parameter (for intramodular connections), we were able to simulate both findings in Kwapil's schizophrenia study group, i.e. increased priming and decreased overall memory recall. By increasing this parameter from 0.0106 to 0.0148, the level of intracategory pruning increased from 36.5% to 61.8% and that of intracase pruning increased from 83.2% to 93.5% (see Table 1). This manipulation enhanced priming and reduced performance in a way that closely approximated the empirical findings for patients with schizophrenia reported by Kwapil et al (Reference Kwapil, Hegley and Chapman1990).
DISCUSSION
Modelling approach
The first aim of this study was to simulate a neural network that would quantitatively emulate semantic priming in a normal population, and then to alter that network using the smallest number of parameters that would recreate the performance exhibited by patients with schizophrenia. A 120-neuron network makes gross simplifications, as any initial modelling or theory-building effort must. We do not claim that it captures the richness and complexity of actual human cognition, but we feel that it illustrates some possible relationships between microscopic (neural) interactions and macroscopic (clinical) observations.
Implications regarding mechanism of priming
Semantic priming is a well-characterised process that is central to understanding the human cognitive functions of learning and memory. It allows for more efficient recognition of categorically similar items and allows one to stay in a particular semantic ‘set’ (as opposed to switching sets). Our study shows how this cognitive capacity can emerge in a distributed network and sheds light, more generally, on how meanings may be encoded neurally. Our findings call into question theories of cognition based on local representation — i.e. that a given concept is represented in an individual neuron or node.
Our simulation builds on the work of Hermann et al (Reference Hermann, Ruppin and Usher1993), who also observed semantic priming using a distributed network model. They created a neural network with adaptation incorporated at the activation function level, and employed memories of distinct semantic classes, each of which was defined by a ‘fuzzy core’ of similarity at the neuronal level. Their network also exhibited priming behaviour in its normally functioning state. While their model is informative, it does not consider the possible effects of selective elimination of intrinsic corticocortical neuronal processes, a normal component of postnatal development, in producing semantic priming in health and possibly in schizophrenia.
Our model simulated not only enhanced priming but also cognitive impairment. Specifically, the model's non-primed recall performance declined as schizophrenogenic pruning increased. This can be understood as the analogue of the cognitive impairments seen in actual patients with schizophrenia. Such impairments are demonstrated in the study by Kwapil et al, where participants in the schizophrenia group performed worse (by about 10%) than the control group on baseline degraded stimuli recognition tests (the schizophrenia group had a correct response rate of 43.0% and the normal group 48.1%, as shown in Table 2), as well as a large number of experimental studies.
Correlation with neuroanatomic studies
Our results estimated reductions in connectivity associated with normal as well as schizophrenic development. By using a methodology described by Hoffman & McGlashan (Reference Hoffman and McGlashan1997), the model can also be used to estimate corresponding reductions in synapses. These estimates can be generated if one assumes that the number of synapses mediating a projection from one neuron to another is linearly correlated with the strength or weight of that projection. Using this technique, we calculated the reduction in synapses in moving from the control to the schizophrenia case to be 32.3%. This is roughly similar to results obtained by Glantz & Lewis (Reference Glantz and Lewis2000) — their study indicated that dendritic spine density of layer III pyramidal neurons in the dorsolateral prefrontal cortex (DLPFC area 46) was decreased by 23% in schizophrenia compared with normal brains. Based on the confidence interval that they provide, our model's predictions fall well within one standard deviation of their results. Our study also has parallels with the work of Benes et al (Reference Benes, McSparren and Bird1991), who showed that in the brains of patients with schizophrenia interneurons were reduced in most layers of cingulate cortex.
Neurodevelopment and the ‘disconnection’ syndromes
The feasibility of pruning as a central neuro-developmental event leading to full adult cognitive functioning is supported by Woo et al (Reference Woo, Pucak and Kye1997). Their study comparing prepubertal and mature monkeys showed that in the course of development considerable synaptic pruning occurred in the prefrontal cortex and that this process involved primarily short, intrinsic, within-region connections. Specifically, they found much greater synaptic elimination among the intrinsic axon projections of the supragranular pyramidal neurons than among the relatively longer association fibres connecting different cortical regions. This neurodevelopmental pattern was also seen by Lewis & Gonzalez-Burgos (Reference Lewis and Gonzalez-Burgos2000), who argued that the local, intrinsic connections in the prefrontal cortex are an important anatomic substrate for the development of working memory functions and that the selective elimination of these connections at adolescence could underlie schizophrenic symptomatology. If schizophrenia reflects an extension of normal adolescent pruning we would expect short connections to be eliminated selectively — precisely the connections that our model predicts are deficient.
Our findings can also be understood in the context of the ‘disconnection’ syndromes described by Friston (Reference Friston1996) among others. This theoretical approach views schizophrenia as a failure of functional integration, which can be looked at in neuropathological terms as a deficit in anatomic, functional or effective connectivity. Moreover, these researchers describe neuroimaging methodologies that permit assessment of functional connectivity. The model described here assumes an anatomic disconnection syndrome specifically involving local level intrinsic connectivity. In particular, our findings suggest that the elucidation of both normal neuro-development and schizophrenia may benefit from future studies combining measures of semantic priming and functional corticocortical connectivity based on neuroimaging methods.
Clinical Implications and Limitations
CLINICAL IMPLICATIONS
-
• When considered in the light of animal studies, the results reported here suggest that late cortical pruning associated with adolescence is the neurodevelopmental process most closely linked to the genesis of schizophrenia.
-
• Further evidence is provided that cortical connectivity is reduced in patients with schizophrenia.
-
• Local cortical connections appear to be especially vulnerable to excessive pruning in schizophrenia.
LIMITATIONS
-
• The 120-neuron model described here necessarily makes simplifying assumptions and cannot capture the full richness and complexity of human cognition.
-
• The proper methodology to use in making statistical comparisons between computer-model-generated data and clinical data is not entirely clear.
-
• Recent studies failing to find increased priming in people with schizophrenia suggest that it may be a characteristic of a subset of patients, rather than a general phenomenon.







eLetters
No eLetters have been published for this article.