If at some radius r = rj there is a jump of the density and composition then a simple asymptotic formula can be derived which gives ω, the oscillation frequency for large degree modes (ℓ ≫ 1). Using relations of Gabriel and Scuflaire (1979) and taking into account the fact that the oscillation amplitude at R < rj or R > rj is equal to rℓ or r−ℓ multiplied by some functions only weakly dependent on ℓ, we obtain 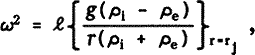where g is the gravitational acceleration, and ρi(ρe) are the densities at the lover (upper) sides of the layer in question. The comparison with the exact ω-values considered below shows that the asymptotic values are larger by 13, 8.8, and 6 percents for ℓ equal to 5, 7, and 10, respectively. Because ω should be less than the maximum value of the Brunt - Väisälä frequency, we have for a finite thickness Δ of the jump layer and for finite ℓ that ℓ ≪ 2rj/Δ. We have performed numerical study of the above modes which may be called interior modes. The equilibrium model was similar to that studied by Vandakurov (1984 a,b) but now we assume that a small iron-like core (as in Rouse's (1983) model) is present. We assume the hydrogen content in the core to be large enough for convection to occur. Above the core, there are the inhomogeneous convectively neutral zone (rj ≤ r ≤ rj1), the homogeneous radiative zone (rj1 ≤ r ≤ ru), and the convective envelope (ru ≤ r ≤ R), whose structure have been taken from Spruit's (1974) paper.