No CrossRef data available.
Article contents
Nonlinear Surface Alfvén Wave Propagation in Solar Atmosphere
Published online by Cambridge University Press: 19 July 2016
Extract
The paper deals with the surface wave propagation in the solar atmosphere. The plasma motion is supposed to be described by magnetohydrodynamic equations. In the first part of the paper the surface wave propagation on a single magnetic interface in the solar corona is considered. The plasma is assumed to be cold. Using the reductive perturbation method we derive the equation governing the evolution of nonlinear small-amplitude surface waves as follows
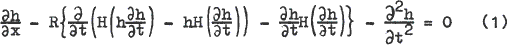 This equation is written in a coordinate system moving with the phase velocity of linear waves. Dimensionless variables are used. The symbol H denotes the Hilbert transform. The shape of the interface is defined by the equation z = h(t,x) in the Cartesian coordinates x, y, z. The Reynolds number R determines the relative contributions of nonlinearity and viscosity. We take a source radiating a sinusoidal wave. Then the wave evolution is calculated numerically. We get that at large R the wave steepening takes place. This steepening leads to a strong increase of wave damping.
This equation is written in a coordinate system moving with the phase velocity of linear waves. Dimensionless variables are used. The symbol H denotes the Hilbert transform. The shape of the interface is defined by the equation z = h(t,x) in the Cartesian coordinates x, y, z. The Reynolds number R determines the relative contributions of nonlinearity and viscosity. We take a source radiating a sinusoidal wave. Then the wave evolution is calculated numerically. We get that at large R the wave steepening takes place. This steepening leads to a strong increase of wave damping.
- Type
- VI. Chromospheric and Coronal Heating
- Information
- Symposium - International Astronomical Union , Volume 142: Basic Plasma Processes on the Sun , 1990 , pp. 237 - 238
- Copyright
- Copyright © Kluwer 1990


