Article contents
Morphology and Power of Radio Sources
Published online by Cambridge University Press: 14 August 2015
Extract
I want to make two points:
1. Observations suggest that the hot-spots move about either because the beam precesses (e.g. Ekers et al. 1978; Lonsdale & Morrison 1980) or more discontinuously, as in sources like 3C351 that have multiple hot-spots (Laing 1981). The natural interpretation is that the hot-spot at the end of the beam slides over the inner surface of a ‘cavity’ filled with very hot dilute ex-hot-spot material (Scheuer 1974), extending the cavity at various places at different times. Such a ‘dentist's drill’ model has various consequences:
(i) The mean speed (length/age) at which the cavity elongates may be considerably smaller than the instantaneous speed V of the hot-spot, estimated in the customary way from pressure balance:
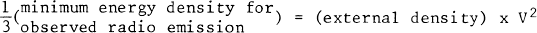
(ii) Remark (i) raises the possibility that giant radio sources have become so long because their jets are unusually constant in direction. NGC6251, which is over 2 Mpc long, has a jet whose direction has not wavered by more than a few degrees in ∼ 107 years (Saunders et al. 1981).
(iii) We should not be surprised by sources whose hot-spots lie some way behind the extreme ends of the source; this may merely mean that the beam at present impinges on one side of the ‘cavity’. 3C285 is a typical example; a more persuasive case is the Np component of 3C219 (Perley et al. 1980).
2. Most of the radio emission of most really powerful radio sources comes from their hot spots. Contrariwise, straightforward equipartition calculations on models lead to at least as much emission from the ‘cavity’ as from the hot-spots (Scheuer 1974). While there are several possible explanations, one in particular is suggested by Laing's (1981) extensive data on 40 sources. He lists the synchrotron lifetimes in the hot-spots for electrons radiating at 15 GHz, and while these exceed the light crossing times, they do so by only one or two orders of magnitude. One expects flow through the hot spots at some fairly small fraction of the speed of light; the synchrotron loss cutoff in the hot-spot is then expected to appear in the mm or infra-red region. Expansion of the hot-spot material into the cavity shifts the loss cutoff to a much lower frequency. If the expansion is adiabatic (certainly an oversimplification) the ratio of loss cutoff frequencies is equal to the ratio of energy densities. We cannot use this relationship directly in the more interesting cases, as we cannot estimate the energy density (or even the size) of a ‘cavity’ that we cannot observe. However, we can estimate the cutoff frequency within the hot-spots (for some assumed streaming speed), and Figure 1 shows that the most powerful hot-spots have loss cutoff frequencies in the 10–100 GHz range, implying cutoff frequencies in the ‘cavity’ that could well be below 1 GHz.
- Type
- Research Article
- Information
- Symposium - International Astronomical Union , Volume 97: Extragalactic Radio Sources , 1982 , pp. 163 - 165
- Copyright
- Copyright © Reidel 1982
References
- 31
- Cited by


