No CrossRef data available.
Published online by Cambridge University Press: 08 February 2017
One region where discrepancies between the seismic and standard solar models continue to exist is the overshoot layer below the convective zone (Gough et al. 1996). A main reason for this discrepancy is clearly the lack of a realistic physical model for astrophysical overshoot. Beside numerical experiments, the most promising approach to the construction of such a model is based on the Reynolds-stress formalism of turbulence theory (Speziale 1991). As a first step toward the development of a more complete Reynolds stress model of the overshoot, here we present a simple κ-ϵ model, valid under the following conditions:
(a). Incompressibility: ∂iVi = 0. Owing to the short length scale (cf. Fig. 1), this assumption is somewhat better founded here than in other models.
(b). Closure: Let 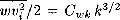 and
and 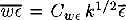 . (w = vz vertical velocity; κ ≡ V2/2: kinetic energy; ϵ: dissipation rate). Now assume Cwk = const., Cwt =const. This is warranted if l/Hv ≃constant (Hv: scale height of V2), which will be seen indeed to be the case in our model, cf. eqs. (3)–(4).
. (w = vz vertical velocity; κ ≡ V2/2: kinetic energy; ϵ: dissipation rate). Now assume Cwk = const., Cwt =const. This is warranted if l/Hv ≃constant (Hv: scale height of V2), which will be seen indeed to be the case in our model, cf. eqs. (3)–(4).
(c). No correlation with thermodynamic fluctuations: 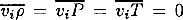 . The assumption implies that these correlations vanish in a very thin (≪ Hp) transition layer below △▽ = 0. No change in the geometrical flow properties is expected in such a thin layer, so lo, Cwk, and Cwϵ should be the same as in the lower part of the unstable layer. On the basis of numerical experiments here we use lo = HP, Cwk = 0.6, Cwϵ = 3, q = 2.4. (The index ‘0’ refers to values at z = 0 i.e. at △▽ = 0.) Note however that V may be significantly reduced in the transition layer, so Vo (and thus
. The assumption implies that these correlations vanish in a very thin (≪ Hp) transition layer below △▽ = 0. No change in the geometrical flow properties is expected in such a thin layer, so lo, Cwk, and Cwϵ should be the same as in the lower part of the unstable layer. On the basis of numerical experiments here we use lo = HP, Cwk = 0.6, Cwϵ = 3, q = 2.4. (The index ‘0’ refers to values at z = 0 i.e. at △▽ = 0.) Note however that V may be significantly reduced in the transition layer, so Vo (and thus 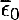 ) is undetermined in the present model.
) is undetermined in the present model.