Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-25T18:00:01.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Itinerancy of Quasiequilibria in One-Dimensional Gravitating Systems

Published online by Cambridge University Press:  25 May 2016

T. Tsuchiya ,
N. Gouda  and
T. Konishi
T. Tsuchiya
Affiliation:
National Astronomical Observatory, Mitaka, 181, Japan
N. Gouda
Affiliation:
Department of Earth and Space Science, Osaka University, Toyonaka, 560, Japan
T. Konishi
Affiliation:
Department of Physics, Nagoya University, Nagoya, 464-01, Japan

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One-dimensional self-gravitating many-body systems consist of N identical parallel sheets which have uniform mass density m and infinite in extent in the (y, z) plane. We call the sheets particles in this paper. The particles are free to move along x axis and accelerate as a result of their mutual gravitational attraction. The Hamiltonian of this system has a form of 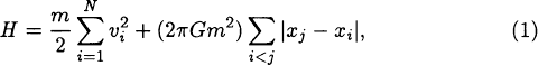where m, vi, and xi are the mass (surface density), velocity, and position of ith particle respectively.

Type
Stellar Dynamics, Models
Information
Symposium - International Astronomical Union , Volume 174: Dynamical Evolution of Stars Clusters , 1996 , pp. 385 - 386
Copyright
Copyright © Kluwer 1996 

References

Luwel, M. and Severne, G. (1985) Collisionless mixing in 1-dimensional gravitational systems initially in a stationary waterbag configuration, Astron. Astrophys., Vol. 152, pp. 305.Google Scholar
Miller, B.N. (1991) Gravity in One Dimension: Diffusion in Acceleration, J. Stat. Phys., Vol. 63, pp. 291.Google Scholar
Severne, G. and Luwel, M. (1986) Violent relaxation and mixing in non-uniform one-dimensional gravitational systems, Astrophys. and Space Sci., Vol. 122, pp. 299.Google Scholar
Tsuchiya, T., Tetsuro, K. and Gouda, N. (1994) Quasi-equilibria in one-dimensional self-gravitating many body systems, Phys. Rev. E, Vol. 50, pp. 2706.Google Scholar
Tsuchiya, T., Gouda, N. and Tetsuro, K. (1995) Relaxation processes in one-dimensional self-gravitating many-body systems, Phys. Rev. E, submitted.Google Scholar