To maintain the spiral structure over long periods in spite of the chaotic disturbances so often seen in galaxies it is probably necessary to have a large energy store which is gradually tapped to generate and maintain the spiral wave. Now in a sense stable axially symmetrical model galaxies are configurations of minimum energy for a given angular momentum structure. By a given angular momentum structure I mean that the function μ(h)dh giving the total mass with specific angular momentum between h and h + dh is given and in making the minimum energy statement I have assumed that there is sufficient ‘random’ motion to satisfy Toomre's local stability criterion. To tap a store of energy one must either tap the energy of the whole rotational structure by finding disturbances that may change μ(h), or one may tap the smaller energy store of the ‘random’ motions. Clearly the larger energy store is the more attractive. Now μ(h) is conserved for any axially symmetrical time dependent motions so the only disturbances that can change μ(h) are non-axially symmetrical. If one considers a single star moving in nearly circular motion and interacting with a weak disturbance in the gravitational potential which may be Fourier analysed into components of the form S(R) exp[i(mΦ+ωt)] then one finds that the energy and angular momentum of the star oscillate but do not change in the mean. This statement is untrue when the force due to the wave does not average to zero or when it resonates with the natural oscillation of the star about the circular motion. The angular frequency of the force seen by the star is ω + mΩ, where Ω(R) is the rotational angular velocity of the galaxy, so the exceptions occur at the resonances 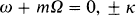Here κ(R) = (4B(B-A))1/2, the epicyclic angular frequency, and A(R) and B(R) are Oort's constants. At the radius where ω + mΩ(R) = 0 the pattern of the disturbance moves around at the same velocity as the circular motion of the stars epicentre. The other resonances that were discovered by B. Lindblad lie one within and one outside that circle.