Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Using the [(2+1)+1]-dimensional representation of the Einstein equations, we have computed the general relativistic collapse of a rotating star. We adopt the cylindrical coordinate. The system is assumed to be axially and plane symmetric. The number of meshes is 28×28 in R and Z direction. The equation of state is P=1/3ρε for ρ< ρ*≡3×1014 g/cm3 and P=(ρ-ρ*)ε+1/3ρ*ε for 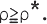 We use the following initial conditions; ρ∝exp(-(R2+Z2)/λ), Ω∝exp(-R2/λ) where Ω and λ are angular velocity and a size parameter, respectively. We have calculated three models;
We use the following initial conditions; ρ∝exp(-(R2+Z2)/λ), Ω∝exp(-R2/λ) where Ω and λ are angular velocity and a size parameter, respectively. We have calculated three models;
(1) Model 1 M=10M⊙, ρc=3×1013g/cm3, α=0.20, β=0.05.
(2) Model 2 M=10M⊙, ρc=3×1013g/cm3, α=0.20, β=0.12.
(3) Model 3 M=10M⊙, ρc=3×1013g/cm3, α=0.20, β=0.22.
where α=E
int/|E
grav| and β=E
rot/|E
grav|. In all models, an apparent horizon was formed, that is, a black hole was formed. In Model 1, the final density distribution is oblate shape. In Model 2, there is a ringlike peak of the proper mass density distribution at the final stage. In Model 3, the determinant of the metric tensor goes to nearly zero at the ring in the equatorial plane, so that the proper mass density shows strong ringlike peak which is inside the apparent horizon. As the curvature invariant made from the Riemann tensor becomes very large at this ring, this may be a ring singularity of the space-time. These rotating black holes look like the Kerr black hole.
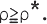 We use the following initial conditions; ρ∝exp(-(R2+Z2)/λ), Ω∝exp(-R2/λ) where Ω and λ are angular velocity and a size parameter, respectively. We have calculated three models;
We use the following initial conditions; ρ∝exp(-(R2+Z2)/λ), Ω∝exp(-R2/λ) where Ω and λ are angular velocity and a size parameter, respectively. We have calculated three models;