No CrossRef data available.
Article contents
From 2-D to 3-D by Maximum Entropy Method
Published online by Cambridge University Press: 03 August 2017
Extract
We present a method of estimating distances to clusters of galaxies from twodimensional catalogues. The angular diameters (or magnitudes) of galaxies are used as distance indicators. The mapping from 2-D to 3-D is done by using a ‘diameter function’ (analogous to a luminosity function), which is based on a redshift survey from a section of the sky. The problem is formulated as follows. The number of galaxies with a metric diameter D in a volume element d3r is:
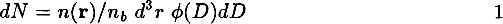 where n(r) is the ‘true’ number density of galaxies at position r, n& is the mean number density of galaxies in the universe and ϕ(D)dD is the diameter function. We assume that within a narrow cone n(r) = n(r) and then express N(> θ), the number of galaxies greater than a certain angular diameter θ. In a discrete form we write the relation as:
where n(r) is the ‘true’ number density of galaxies at position r, n& is the mean number density of galaxies in the universe and ϕ(D)dD is the diameter function. We assume that within a narrow cone n(r) = n(r) and then express N(> θ), the number of galaxies greater than a certain angular diameter θ. In a discrete form we write the relation as:
 where ni is the density at the i – th distance bin and Pik is our ‘point spread function’, which is a function of the diameter function and Galactic obscuration. We express (2) in terms of χ2 statistics over the measurements, and require it to be less than a certain value. The entropy of the image is expressed as:
where ni is the density at the i – th distance bin and Pik is our ‘point spread function’, which is a function of the diameter function and Galactic obscuration. We express (2) in terms of χ2 statistics over the measurements, and require it to be less than a certain value. The entropy of the image is expressed as:
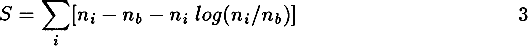
- Type
- Appendix 1: Poster Papers
- Information
- Copyright
- Copyright © Reidel 1988


