The space surrounding a long straight cosmic string is flat but conical. The conical topology implies that such a string focuses light rays or particles passing by opposite sides of the string, which can have important astrophysical effects. The flatness, however, implies that the string has no gravitational influence on matter at rest with respect to the string. The flatness is a consequence of the fact that the tension along a cosmic string is equal to its linear mass density μ. There may be physical effects, however, which destroy the equality of tension and mass density, so that straight strings might after all affect matter at rest. One such effect we and others have calculated is the vacuum fluctuations of fields near the strings induced by the conical topology. Such fluctuation s are physically observable but normally small, as in the Casimir effect between parallel plates. We find the vacuum expectation value of the stress - energy tensor of a conformally coupled scalar field around a cosmic string to be 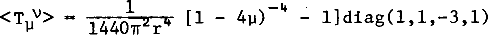in cylindrical coordinates (t, r, θ, z). The equality of Ttt and Tzz means that the effective tension and mass density of the vacuum fluctuations are equal, so that at least in a semiclassical approximation a string dressed by such fields still has no gravitational influence on matter at rest, even though it has a substantial mass density.