Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T07:34:02.266Z Has data issue: false hasContentIssue false
  • English
  • Français

The Anisotropy of the Microwave Background: Space Experiment Relict

Published online by Cambridge University Press:  03 August 2017

I.A. Strukov ,
D.P. Skulachev ,
A.A. Klypin  and
M.V. Sazhin
I.A. Strukov
Affiliation:
Space Research Institute, Academy of Sciences, Moscow
D.P. Skulachev
Affiliation:
Space Research Institute, Academy of Sciences, Moscow
A.A. Klypin
Affiliation:
Space Research Institute, Academy of Sciences, Moscow
M.V. Sazhin
Affiliation:
Sternberg State Astronomical Institute, Moscow

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We carried out the first satellite experiment for searching the anisotropies of the microwave background. The main goal of the experiment was to obtain a radio brightness map of the sky at 8 mm. We obtained the direction and amplitude of the dipole component at 90% confidence level 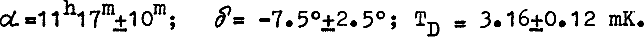The variance analysis gives the most stringent constraints on fluctuations of the relic background. For the model with the Zeldovich spectrum of primordial fluctuations we found an upper limit on the quadrupole as 1.6×10−5 at 95% level. We are first to obtain model-independent estimates of the first 15 multipole components. We obtained upper limits on correlation function of angular fluctuations 〈ΔT1ΔT2〉 = 0.005 mK2 for the angular range from 20° to 160°. Intense galactic emission was observed over longitude interval from 90° to 270° and latitudes ±5°. The total flux from this longitude interval is approximately 56,000 Jy. The experiment studies confirmed that a space experiment gives a possibility to reach sensitivities high enough to estimate an anisotropy that is less than the values predicted by modern cosmological models.

Type
Research Article
Information
Symposium - International Astronomical Union , Volume 130: Large Scale Structures of the Universe , 1988 , pp. 27 - 34
Copyright
Copyright © Reidel 1988 

References

Abbott, L.F. and Wise, M.B. 1984, Ap. J. 282, L47.Google Scholar
Birkinshaw, M., Gull, S.F. and Hardebeck, H. 1984, Ap. J. 309, 34.Google Scholar
Boughn, S., Cheng, E. and Wilkinson, D.T. 1981, Ap. J. (Letters) 243, L113.Google Scholar
Boyarski, M. 1986, Report at VI Vsesojusn. Symp. Teor. and Pricl. Mekhanika, Tashkent, 1986.Google Scholar
Doroshkevich, A.G., Klypin, A.A. and Khlopov, M.U. 1986, Pis'ma v Astron. Zh. 12, 412.Google Scholar
Elyasberg, P. and Tymokhova, T. 1986, Space Research XXIV, 4, 497.Google Scholar
Elyasberg, P., Tymokhova, T. and Boyarski, M. 1986, Report at the Symposium on Flight Dynamics, European Space Operation Center in Darmstadt, West Germany.Google Scholar
Fixsen, D.J., Cheng, E.S. and Wilkinson, D.T. 1983, Phys. Rev. Letters 50, 620.Google Scholar
Guth, A. 1981, Phys. Rev. B23, 347.Google Scholar
Henry, P.S. 1971, Nature 231, 516.Google Scholar
Kofman, L.A., Pogosyan, D.U. and Starobinski, A.A. 1986, Pis'ma v Astron. Zh. 12, 419.Google Scholar
Kofman, L.A. and Starobinski, A.A. 1985, Pis'ma v Astron. Zh. 11, 643.Google Scholar
Linde, A.D. 1982, Phys. Letters B108, 389.Google Scholar
Linde, A.D. 1985, Phys. Letters B158, 375.CrossRefGoogle Scholar
Lubin, P.M. 1984, Third Rome Meeting Astrophysics, Dec. 1984. Prepr.Google Scholar
Lubin, P.M., Villela, T.V., Epstein, G.L. and Smoot, G.F. 1985, Ap. J. 298, L1.CrossRefGoogle Scholar
Mezger, P.G. 1978, Astron. and Ap. 70, 565.Google Scholar
Rubakov, V.A., Sazhyn, M.V. and Verjaskin, A.V. 1982, Phys. Letters B115, 189.Google Scholar
Starobinski, A.A. 1980, Phys. Letters B91, 99.Google Scholar
Starobinski, A.A. 1983, Pis'ma v Astron. Zh. 9, 579.Google Scholar
Strukov, I.A. and Skulachev, D.P., SSR/Ap. and Space Physics 6. In preparation.Google Scholar
Strukov, I.A., Skulachev, D.P. and Tkachev, A.N. 1987, Sci. Instrum. for Space Research. In preparation.Google Scholar
Sunyaev, R.A. and Zeldovich, Ya.B. 1970, Ap. Sp. Sci. 7, 13.Google Scholar