Article contents
Vectorial parameterizations of pose
Published online by Cambridge University Press: 10 December 2021
Abstract
Robotics and computer vision problems commonly require handling rigid-body motions comprising translation and rotation – together referred to as pose. In some situations, a vectorial parameterization of pose can be useful, where elements of a vector space are surjectively mapped to a matrix Lie group. For example, these vectorial representations can be employed for optimization as well as uncertainty representation on groups. The most common mapping is the matrix exponential, which maps elements of a Lie algebra onto the associated Lie group. However, this choice is not unique. It has been previously shown how to characterize all such vectorial parameterizations for SO(3), the group of rotations. Some results are also known for the group of poses, where it is possible to build a family of vectorial mappings that includes the matrix exponential as well as the Cayley transformation. We extend what is known for these pose mappings to the 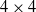 $4 \times 4$
representation common in robotics and also demonstrate three different examples of the proposed pose mappings: (i) pose interpolation, (ii) pose servoing control, and (iii) pose estimation in a pointcloud alignment problem. In the pointcloud alignment problem, our results lead to a new algorithm based on the Cayley transformation, which we call CayPer.
$4 \times 4$
representation common in robotics and also demonstrate three different examples of the proposed pose mappings: (i) pose interpolation, (ii) pose servoing control, and (iii) pose estimation in a pointcloud alignment problem. In the pointcloud alignment problem, our results lead to a new algorithm based on the Cayley transformation, which we call CayPer.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 4
- Cited by


