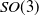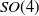1. Introduction
In kinematics, it is natural to ask how large a rigid-body motion is and how to choose a meaningful weighting for the rotational and translational portions of the motion. For example, given the
![]() $(n+1)\times (n+1)$
homogeneous transformation matrix
$(n+1)\times (n+1)$
homogeneous transformation matrix
that describes a rigid-body displacement in
![]() $\mathbb{R}^n$
, how far is it from the
$\mathbb{R}^n$
, how far is it from the
![]() $(n+1)\times (n+1)$
identity matrix
$(n+1)\times (n+1)$
identity matrix
![]() $\mathbb{I}_{n+1}$
(which is the homogeneous transformation describing the null motion)? Having a kinematic distance metric
$\mathbb{I}_{n+1}$
(which is the homogeneous transformation describing the null motion)? Having a kinematic distance metric
![]() $d(\cdot, \cdot )$
allows one to give a numerical answer:
$d(\cdot, \cdot )$
allows one to give a numerical answer:
![]() $d(H, \mathbb{I}_{n+1})$
.
$d(H, \mathbb{I}_{n+1})$
.
Then, for example, the problem of serial manipulator inverse kinematics which is usually stated as solving the homogeneous transformation equation
for
![]() $\{\theta _i\}$
instead becomes a problem of minimizing the cost
$\{\theta _i\}$
instead becomes a problem of minimizing the cost
Such reformulations of inverse kinematics can be particularly useful for binary-actuated systems where resolved rate methods can be difficult to apply given the discontinuous nature of binary actuators [Reference Suthakorn and Chirikjian1].
Another class of examples where metrics can be employed is in problems in sensor calibration such as solving
![]() $A_i X=YB_i$
for
$A_i X=YB_i$
for
![]() $X$
and
$X$
and
![]() $Y$
[Reference Li, Ma, Wang and Chirikjian2] and solving
$Y$
[Reference Li, Ma, Wang and Chirikjian2] and solving
![]() $A_iXB_i = YC_i Z$
for
$A_iXB_i = YC_i Z$
for
![]() $X,Y,Z$
[Reference Ma, Goh, Ruan and Chirikjian3] given sets of homogeneous transformations
$X,Y,Z$
[Reference Ma, Goh, Ruan and Chirikjian3] given sets of homogeneous transformations
![]() $\{A_i\}$
,
$\{A_i\}$
,
![]() $\{B_i\}$
, and
$\{B_i\}$
, and
![]() $\{C_i\}$
. Using metrics, these become problems of minimizing the cost functions
$\{C_i\}$
. Using metrics, these become problems of minimizing the cost functions
and
Sometimes the sum of distances is replaced with sum of squares, to remove square roots from computations.
A number of metrics (or distance functions) have been proposed in the kinematics literature to address the sorts of problems described above. Whereas every metric must, by definition, be symmetric and satisfy the triangle inequality, additional invariance properties are also useful [Reference Amato, Bayazit, Dale, Jones and Vallejo4–Reference Chirikjian6]. For a recent summary, see [Reference Di Gregorio7].
A seemingly unrelated body of literature in the field of statistical mechanics is concerned with the inequality
where
![]() $\exp (\cdot )$
is the matrix exponential and
$\exp (\cdot )$
is the matrix exponential and
![]() $A$
and
$A$
and
![]() $B$
are Hermitian matrices of any dimension. This is the Golden-Thompson inequality which was proved in 1965 independently in refs. [Reference Golden8] and [Reference Thompson9]. In this article, we prove that the inequality (2) also holds when
$B$
are Hermitian matrices of any dimension. This is the Golden-Thompson inequality which was proved in 1965 independently in refs. [Reference Golden8] and [Reference Thompson9]. In this article, we prove that the inequality (2) also holds when
![]() $A$
and
$A$
and
![]() $B$
are
$B$
are
![]() $3\times 3$
or
$3\times 3$
or
![]() $4\times 4$
skew-symmetric matrices of bounded norm. Though it has been stated in the literature that (2) extends to the case when
$4\times 4$
skew-symmetric matrices of bounded norm. Though it has been stated in the literature that (2) extends to the case when
![]() $A$
and
$A$
and
![]() $B$
are Lie-algebra basis elements, with attribution often given to Kostant [Reference Kostant10], in fact, it is not true unless certain caveats are observed, as will be discussed in Section 3.
$B$
are Lie-algebra basis elements, with attribution often given to Kostant [Reference Kostant10], in fact, it is not true unless certain caveats are observed, as will be discussed in Section 3.
2. Related work
2.1. SO(3) distance metrics and Euler’s theorem
2.1.1. Upper bound from trace inequality
As will be shown in Section 3, (2) holds for skew-symmetric matrices with some caveats. This is relevant to the topic of
![]() $SO(3)$
matrices. It is well known that by Euler’s theorem, every
$SO(3)$
matrices. It is well known that by Euler’s theorem, every
![]() $3\times 3$
rotation matrix can be written as
$3\times 3$
rotation matrix can be written as
where
![]() $\textbf{n}$
is the unit vector in the direction of the rotation axis,
$\textbf{n}$
is the unit vector in the direction of the rotation axis,
![]() $\hat{\textbf{n}}$
is the unique skew-symmetric matrix such that
$\hat{\textbf{n}}$
is the unique skew-symmetric matrix such that
for any
![]() $\textbf{v} \in \mathbb{R}^3$
,
$\textbf{v} \in \mathbb{R}^3$
,
![]() $\times$
is the cross product, and
$\times$
is the cross product, and
![]() $\theta$
is the angle of the rotation. Letting
$\theta$
is the angle of the rotation. Letting
![]() $\textbf{n}$
roam the whole sphere and restricting
$\textbf{n}$
roam the whole sphere and restricting
![]() $\theta \in [0,\pi ]$
covers all rotations, with redundancy at a set of measure zero. Since
$\theta \in [0,\pi ]$
covers all rotations, with redundancy at a set of measure zero. Since
from this equation,
![]() $\theta$
can be extracted from
$\theta$
can be extracted from
![]() $R$
as
$R$
as
It can be shown that given two rotation matrices, then a valid distance metric is [Reference Park11]
It is not difficult to show that this satisfies symmetry and positive definiteness. However, proving the triangle inequality is more challenging. But if the Golden-Thompson inequality (2) can be extended to the case of skew-symmetric matrices, it would provide a proof of the triangle inequality of the above
![]() $\theta (R_1^T R_2)$
distance metric. In order to see this, assume that
$\theta (R_1^T R_2)$
distance metric. In order to see this, assume that
with
![]() $\theta _1 \in [0,\pi ]$
and
$\theta _1 \in [0,\pi ]$
and
![]() $\theta _2 \in [0,\pi ]$
. It is not difficult to see that
$\theta _2 \in [0,\pi ]$
. It is not difficult to see that
since
and
![]() $\textbf{n}_1 \cdot \textbf{n}_2 \in [-1,1]$
. On one hand, if
$\textbf{n}_1 \cdot \textbf{n}_2 \in [-1,1]$
. On one hand, if
![]() $\|\theta _1 \textbf{n}_1 +\theta _2 \textbf{n}_2 \| \leq \pi$
and (2) does hold for skew-symmetric matrices, then computing
$\|\theta _1 \textbf{n}_1 +\theta _2 \textbf{n}_2 \| \leq \pi$
and (2) does hold for skew-symmetric matrices, then computing
and
and observing (2) would give
But the function
![]() $f(\theta ) = 1 + 2 \cos \theta$
is monotonically nonincreasing when
$f(\theta ) = 1 + 2 \cos \theta$
is monotonically nonincreasing when
![]() $\theta \in [0, \pi ]$
, so
$\theta \in [0, \pi ]$
, so
![]() $f(\theta ) \leq f(\phi )$
implies
$f(\theta ) \leq f(\phi )$
implies
![]() $\theta \geq \phi$
. Therefore, if (2) holds, then
$\theta \geq \phi$
. Therefore, if (2) holds, then
Then
On the other hand, if
![]() $\|\theta _1 \textbf{n}_1 +\theta _2 \textbf{n}_2 \| \gt \pi$
, then
$\|\theta _1 \textbf{n}_1 +\theta _2 \textbf{n}_2 \| \gt \pi$
, then
Therefore, if the Golden-Thompson inequality can be generalized to the case of skew-symmetric matrices, the result will be stronger than the triangle inequality for the
![]() $SO(3)$
metric
$SO(3)$
metric
![]() $\theta (R_1^T R_2)$
since the latter follows from the former.
$\theta (R_1^T R_2)$
since the latter follows from the former.
2.1.2. Lower bound from quaternion sphere
Alternatively, unit quaternions provide a simple way to encode the axis-angle representation, that is,
and we have the quaternion composition formula [Reference Rodrigues12]
We can show that
![]() $\theta (e^{\theta _1 \hat{\textbf{n}}_1}e^{\theta _2 \hat{\textbf{n}}_2})$
is bounded from below such that
$\theta (e^{\theta _1 \hat{\textbf{n}}_1}e^{\theta _2 \hat{\textbf{n}}_2})$
is bounded from below such that
provided that
To see this, let
and
 \begin{equation*} \mathcal {Q} = 2\|\textbf {q}(\textbf {n}_1, \theta _1) - \textbf {q}(-\textbf {n}_2, \theta _2)\| = 2 \sqrt {2 - 2\left ( \cos {\frac {\theta _1}{2}}\cos {\frac {\theta _2}{2}} - \textbf {n}_1 \cdot \textbf {n}_2 \sin {\frac {\theta _1}{2}} \sin {\frac {\theta _2}{2}} \right )} = 2 \sqrt {2-2W}. \end{equation*}
\begin{equation*} \mathcal {Q} = 2\|\textbf {q}(\textbf {n}_1, \theta _1) - \textbf {q}(-\textbf {n}_2, \theta _2)\| = 2 \sqrt {2 - 2\left ( \cos {\frac {\theta _1}{2}}\cos {\frac {\theta _2}{2}} - \textbf {n}_1 \cdot \textbf {n}_2 \sin {\frac {\theta _1}{2}} \sin {\frac {\theta _2}{2}} \right )} = 2 \sqrt {2-2W}. \end{equation*}
Let
It is easy to compute the derivative
Thus,
that is,
![]() $\cos{h_*} \geq \frac{2-h_*^2}{2}$
for any
$\cos{h_*} \geq \frac{2-h_*^2}{2}$
for any
![]() $h_* \geq 0$
. Substituting
$h_* \geq 0$
. Substituting
![]() $h_*$
with
$h_*$
with
![]() $\sqrt{2-2W} \in [0, 2]$
gives
$\sqrt{2-2W} \in [0, 2]$
gives
Let
![]() $\beta \in [0, \pi ]$
such that
$\beta \in [0, \pi ]$
such that
![]() $\cos \beta = W$
, we have
$\cos \beta = W$
, we have
![]() $\sqrt{2-2W} \leq \beta$
, that is,
$\sqrt{2-2W} \leq \beta$
, that is,
![]() $\mathcal{Q} = 2\sqrt{2-2W} \leq 2\beta$
. If
$\mathcal{Q} = 2\sqrt{2-2W} \leq 2\beta$
. If
![]() $W \in [0,1]$
, then
$W \in [0,1]$
, then
![]() $\beta \in [0, \frac{\pi }{2}]$
and
$\beta \in [0, \frac{\pi }{2}]$
and
![]() $2\beta \in [0, \pi ]$
. So by (3),
$2\beta \in [0, \pi ]$
. So by (3),
On the other hand, if
![]() $W \in [-1,0)$
, then
$W \in [-1,0)$
, then
![]() $\beta \in [\frac{\pi }{2}, \pi ]$
and
$\beta \in [\frac{\pi }{2}, \pi ]$
and
![]() $2\beta \in [\pi,2\pi ]$
. According to our definition of distance metric,
$2\beta \in [\pi,2\pi ]$
. According to our definition of distance metric,
which does not guarantee to be larger or equal than
![]() $2\|\textbf{q}(\textbf{n}_1, \theta _1) - \textbf{q}(-\textbf{n}_2, \theta _2)\|$
. Geometrically speaking,
$2\|\textbf{q}(\textbf{n}_1, \theta _1) - \textbf{q}(-\textbf{n}_2, \theta _2)\|$
. Geometrically speaking,
![]() $\theta (e^{\theta _1 \hat{\textbf{n}}_1}e^{\theta _2 \hat{\textbf{n}}_2})$
can be regarded as distance between two rotations
$\theta (e^{\theta _1 \hat{\textbf{n}}_1}e^{\theta _2 \hat{\textbf{n}}_2})$
can be regarded as distance between two rotations
![]() $e^{\theta _1 \hat{\textbf{n}}_1}$
and
$e^{\theta _1 \hat{\textbf{n}}_1}$
and
![]() $e^{-\theta _2 \hat{\textbf{n}}_2}$
, which equals to the arc length between
$e^{-\theta _2 \hat{\textbf{n}}_2}$
, which equals to the arc length between
![]() $\textbf{q}(\textbf{n}_1, \theta _1)$
and
$\textbf{q}(\textbf{n}_1, \theta _1)$
and
![]() $ \textbf{q}(-\textbf{n}_2, \theta _2)$
of the quaternion sphere. Furthermore, the arc length
$ \textbf{q}(-\textbf{n}_2, \theta _2)$
of the quaternion sphere. Furthermore, the arc length
![]() $\boldsymbol{s}$
is just the radian angle between
$\boldsymbol{s}$
is just the radian angle between
![]() $\textbf{q}(\textbf{n}_1, \theta _1)$
and
$\textbf{q}(\textbf{n}_1, \theta _1)$
and
![]() $ \textbf{q}(-\textbf{n}_2, \theta _2)$
, that is,
$ \textbf{q}(-\textbf{n}_2, \theta _2)$
, that is,
But the arc length will always be larger than or equal to the Euclidean distance between
![]() $\textbf{q}(\textbf{n}_1, \theta _1)$
and
$\textbf{q}(\textbf{n}_1, \theta _1)$
and
![]() $ \textbf{q}(-\textbf{n}_2, \theta _2)$
, that is,
$ \textbf{q}(-\textbf{n}_2, \theta _2)$
, that is,
which is equivalent to the lower bound discussed above (Fig. 1).

Figure 1. Geometric interpretation of the lower bound inequality, where
![]() $\boldsymbol{s}$
is the arc length between
$\boldsymbol{s}$
is the arc length between
![]() $\textbf{q}(\textbf{n}_1, \theta _1)$
and
$\textbf{q}(\textbf{n}_1, \theta _1)$
and
![]() $\textbf{q}(-\textbf{n}_2, \theta _2)$
on the quaternion sphere, as well as the angle between
$\textbf{q}(-\textbf{n}_2, \theta _2)$
on the quaternion sphere, as well as the angle between
![]() $O\textbf{q}(\textbf{n}_1, \theta _1)$
and
$O\textbf{q}(\textbf{n}_1, \theta _1)$
and
![]() $O\textbf{q}(-\textbf{n}_2, \theta _2)$
.
$O\textbf{q}(-\textbf{n}_2, \theta _2)$
.
2.2. SO(4) distance metrics as an approximation for SE(3) using stereographic projection
It has been known in kinematics for decades that rigid-body motions in
![]() $\mathbb{R}^n$
can be approximated as rotations in
$\mathbb{R}^n$
can be approximated as rotations in
![]() $\mathbb{R}^{n+1}$
by identifying Euclidean space locally as the tangent plane to a sphere [Reference McCarthy13]. This has been used to generate approximately bi-invariant metrics for
$\mathbb{R}^{n+1}$
by identifying Euclidean space locally as the tangent plane to a sphere [Reference McCarthy13]. This has been used to generate approximately bi-invariant metrics for
![]() $SE(3)$
[Reference Etzel and McCarthy14]. Related to this are approaches that use the singular value decomposition [Reference Larochelle, Murray and Angeles15]. As with the
$SE(3)$
[Reference Etzel and McCarthy14]. Related to this are approaches that use the singular value decomposition [Reference Larochelle, Murray and Angeles15]. As with the
![]() $SO(3)$
case discussed above, if the Golden-Thompson inequality can be shown to hold for
$SO(3)$
case discussed above, if the Golden-Thompson inequality can be shown to hold for
![]() $4\times 4$
skew-symmetric matrices, then a sharper version of the triangle inequality would hold for
$4\times 4$
skew-symmetric matrices, then a sharper version of the triangle inequality would hold for
![]() $SO(4)$
metrics.
$SO(4)$
metrics.
This is the subject of Section 3, which is the main contribution of this paper. In that section, it is shown that the Golden-Thompson inequality can be extended from Hermitian matrices to
![]() $4\times 4$
skew-symmetric matrices and therefore to the
$4\times 4$
skew-symmetric matrices and therefore to the
![]() $3\times 3$
case as a special case. But before progressing to the main topic, some trace inequalities that arise naturally from other kinematic metrics are discussed. For example, the distance metric
$3\times 3$
case as a special case. But before progressing to the main topic, some trace inequalities that arise naturally from other kinematic metrics are discussed. For example, the distance metric
is a valid metric where the Frobenius norm of an arbitrary real matrix is
The triangle inequality for matrix norms then gives
Since the trace is invariant under similarity transformations, the above is equivalent to
This is true in any dimension. But in the 3D case, we can go further using the same notation as in the previous section to get
This trace inequality is equivalently written as
2.3. SE(3) metrics as matrix norms and resulting trace inequalities
Multiple metrics for
![]() $SE(3)$
have been proposed over the past decades, as summarized recently in ref. [Reference Di Gregorio7]. The purpose of this section is to review in more detail a specific metric that has been studied in refs. [Reference Fanghella and Galletti16–Reference Martinez and Duffy18]. The concept of this metric for
$SE(3)$
have been proposed over the past decades, as summarized recently in ref. [Reference Di Gregorio7]. The purpose of this section is to review in more detail a specific metric that has been studied in refs. [Reference Fanghella and Galletti16–Reference Martinez and Duffy18]. The concept of this metric for
![]() $SE(3)$
is to induce from the metric properties of the vector 2-norm
$SE(3)$
is to induce from the metric properties of the vector 2-norm
in
![]() $\mathbb{R}^3$
. Since Euclidean distance is by definition invariant to Euclidean transformations, given the pair
$\mathbb{R}^3$
. Since Euclidean distance is by definition invariant to Euclidean transformations, given the pair
![]() $g = (R, \textbf{t})$
, which contains the same information as a homogeneous transformation, and given the group action
$g = (R, \textbf{t})$
, which contains the same information as a homogeneous transformation, and given the group action
![]() $g \cdot \textbf{x} \doteq R\textbf{x} + \textbf{t}$
, then
$g \cdot \textbf{x} \doteq R\textbf{x} + \textbf{t}$
, then
Then, if a body with mass density
![]() $\rho (\textbf{x})$
is moved from its original position and orientation, the total amount of motion can be quantified as
$\rho (\textbf{x})$
is moved from its original position and orientation, the total amount of motion can be quantified as
 \begin{equation} d(g,e) \,\doteq \, \sqrt{\int _{\mathbb{R}^3}\|g\cdot \textbf{x}-\textbf{x}\|^2_2\,\rho (\textbf{x})\,d\textbf{x}} \,. \end{equation}
\begin{equation} d(g,e) \,\doteq \, \sqrt{\int _{\mathbb{R}^3}\|g\cdot \textbf{x}-\textbf{x}\|^2_2\,\rho (\textbf{x})\,d\textbf{x}} \,. \end{equation}
This metric has the left-invariance property
where
![]() $h, g_1, g_2 \in SE(3)$
. This is because if
$h, g_1, g_2 \in SE(3)$
. This is because if
![]() $h = (R,\textbf{t}) \in SE(3)$
, then
$h = (R,\textbf{t}) \in SE(3)$
, then
and
 \begin{align*} &\| h \cdot (g_1 \cdot \textbf {x}) - h \cdot (g_2 \cdot \textbf {x}) \|_2 = \\[6pt] &\|R [g_1\cdot \textbf {x}] + \textbf {t} - R [g_2\cdot \textbf {x}] - \textbf {t}\|_2 \\[6pt] &\quad= \|g_1\cdot \textbf {x}-g_2\cdot \textbf {x}\|_2. \end{align*}
\begin{align*} &\| h \cdot (g_1 \cdot \textbf {x}) - h \cdot (g_2 \cdot \textbf {x}) \|_2 = \\[6pt] &\|R [g_1\cdot \textbf {x}] + \textbf {t} - R [g_2\cdot \textbf {x}] - \textbf {t}\|_2 \\[6pt] &\quad= \|g_1\cdot \textbf {x}-g_2\cdot \textbf {x}\|_2. \end{align*}
It is also interesting to note that there is a relationship between this kind of metric for
![]() $SE(3)$
and the Frobenius matrix norm. That is, for
$SE(3)$
and the Frobenius matrix norm. That is, for
![]() $g = (R, \textbf{t})$
, and the corresponding homogeneous transformation
$g = (R, \textbf{t})$
, and the corresponding homogeneous transformation
![]() $H(g) \in SE(3)$
, the integral in (5) can be computed in closed form, resulting in a weighted norm
$H(g) \in SE(3)$
, the integral in (5) can be computed in closed form, resulting in a weighted norm
where the weighted Frobenius norm is defined as
Here, with weighting matrix
![]() $W=W^T\in \mathbb{R}^{4\times 4}$
is
$W=W^T\in \mathbb{R}^{4\times 4}$
is
![]() $W=\left ( \begin{array}{cc} J & \textbf{0} \\ \textbf{0}^T & M \end{array} \right )$
.
$W=\left ( \begin{array}{cc} J & \textbf{0} \\ \textbf{0}^T & M \end{array} \right )$
.
![]() $M = \int _{\mathbb{R}^3} \rho (\textbf{x})\,d\textbf{x}$
is the mass, and
$M = \int _{\mathbb{R}^3} \rho (\textbf{x})\,d\textbf{x}$
is the mass, and
![]() $ J=\int _{\mathbb{R}^3} \textbf{x} \textbf{x}^{T} \rho (\textbf{x}) \,d\textbf{x}$
has a simple relationship with the moment of inertia matrix of the rigid body:
$ J=\int _{\mathbb{R}^3} \textbf{x} \textbf{x}^{T} \rho (\textbf{x}) \,d\textbf{x}$
has a simple relationship with the moment of inertia matrix of the rigid body:
The metric in (5) can also be written as
Furthermore, for
![]() $g_1, g_2 \in SE(3)$
$g_1, g_2 \in SE(3)$
as explained in detail in ref. [Reference Chirikjian and Zhou5]. When evaluating the triangle inequality for this metric,
gives another kind of trace inequality.
3. Extension of the Golden-Thompson inequality to SO(3) and SO(4)
Motivated by the arguments presented in earlier sections, in this section, the Golden-Thompson inequality is extended to
![]() $SO(3)$
and
$SO(3)$
and
![]() $SO(4)$
. It is well known that the eigenvalues of a
$SO(4)$
. It is well known that the eigenvalues of a
![]() $4 \times 4$
skew-symmetric matrix are
$4 \times 4$
skew-symmetric matrix are
![]() $\{\pm \psi _1 i, \pm \psi _2 i\}$
and eigenvalues of a
$\{\pm \psi _1 i, \pm \psi _2 i\}$
and eigenvalues of a
![]() $3 \times 3$
skew-symmetric matrix are
$3 \times 3$
skew-symmetric matrix are
![]() $\{\pm \psi i, 0\}$
. In the following contents, we will prove that
$\{\pm \psi i, 0\}$
. In the following contents, we will prove that
for
![]() $A$
and
$A$
and
![]() $B$
being
$B$
being
![]() $4 \times 4$
skew-symmetric matrices provided that
$4 \times 4$
skew-symmetric matrices provided that
![]() $|\psi _1| + |\psi _2| \leq \pi$
, where
$|\psi _1| + |\psi _2| \leq \pi$
, where
![]() $\{\pm \psi _1 i, \pm \psi _2 i\}$
are eigenvalues of
$\{\pm \psi _1 i, \pm \psi _2 i\}$
are eigenvalues of
![]() $A+B$
, or for
$A+B$
, or for
![]() $A$
and
$A$
and
![]() $B$
being
$B$
being
![]() $3 \times 3$
skew-symmetric matrices provided that
$3 \times 3$
skew-symmetric matrices provided that
![]() $|\psi | \leq \pi$
, where
$|\psi | \leq \pi$
, where
![]() $\pm \psi i$
are eigenvalues of
$\pm \psi i$
are eigenvalues of
![]() $A+B$
.
$A+B$
.
3.1. 4D case
Let
![]() $A$
be a
$A$
be a
![]() $4 \times 4$
skew-symmetric matrix with its eigenvalues being
$4 \times 4$
skew-symmetric matrix with its eigenvalues being
![]() $\{\pm \theta _1 i, \pm \theta _2 i\}$
. Without loss of generality, we assume that
$\{\pm \theta _1 i, \pm \theta _2 i\}$
. Without loss of generality, we assume that
![]() $\theta _1 \geq \theta _2 \geq 0$
. For every
$\theta _1 \geq \theta _2 \geq 0$
. For every
![]() $A$
, there exists an orthogonal matrix
$A$
, there exists an orthogonal matrix
![]() $P$
such that [Reference Gallier and Xu19]:
$P$
such that [Reference Gallier and Xu19]:
where
 \begin{equation*} \Omega _A = \left [\begin {array}{cccc} 0 & \theta _1 & 0 & 0\\ -\theta _1 & 0 & 0 & 0\\ 0 & 0 & 0 & \theta _2\\ 0 & 0 & -\theta _2 & 0\\ \end {array}\right ]. \end{equation*}
\begin{equation*} \Omega _A = \left [\begin {array}{cccc} 0 & \theta _1 & 0 & 0\\ -\theta _1 & 0 & 0 & 0\\ 0 & 0 & 0 & \theta _2\\ 0 & 0 & -\theta _2 & 0\\ \end {array}\right ]. \end{equation*}
Let
![]() $\Omega _A = \theta _1 \Omega _1 + \theta _2 \Omega _2$
, where
$\Omega _A = \theta _1 \Omega _1 + \theta _2 \Omega _2$
, where
 \begin{equation*} \Omega _1 = \left [\begin {array}{cccc} 0 & 1 & 0 & 0\\ -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end {array}\right ] \ \text {and} \ \Omega _2 = \left [\begin {array}{cccc} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0\\ \end {array}\right ]. \end{equation*}
\begin{equation*} \Omega _1 = \left [\begin {array}{cccc} 0 & 1 & 0 & 0\\ -1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end {array}\right ] \ \text {and} \ \Omega _2 = \left [\begin {array}{cccc} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0\\ \end {array}\right ]. \end{equation*}
Then
where
![]() $A_i = P\Omega _i P^{\intercal }$
. Notice that
$A_i = P\Omega _i P^{\intercal }$
. Notice that
![]() $\Omega _j^3 + \Omega _j = 0$
and
$\Omega _j^3 + \Omega _j = 0$
and
![]() $\Omega _1 \times \Omega _2 = 0 = \Omega _2 \times \Omega _1$
. So,
$\Omega _1 \times \Omega _2 = 0 = \Omega _2 \times \Omega _1$
. So,
and
In other words,
![]() $A_1 \ \text{and} \ A_2$
commute. Thus, we can expand the exponential of
$A_1 \ \text{and} \ A_2$
commute. Thus, we can expand the exponential of
![]() $A$
as follows:
$A$
as follows:
 \begin{equation} \exp{A}= \exp{\left (\sum _{i=1}^{2} \theta _i A_i\right )} = \prod _{i=1}^2 \exp{\left (\theta _i A_i\right )} = \prod _{i=1}^2 \left (I+\sin{\theta _i}A_i + (1-\cos{\theta _i})A_i^2\right ). \end{equation}
\begin{equation} \exp{A}= \exp{\left (\sum _{i=1}^{2} \theta _i A_i\right )} = \prod _{i=1}^2 \exp{\left (\theta _i A_i\right )} = \prod _{i=1}^2 \left (I+\sin{\theta _i}A_i + (1-\cos{\theta _i})A_i^2\right ). \end{equation}
The last equality comes from the fact that
![]() $A_j^3 + A_j = 0$
. Expanding the above equation gives
$A_j^3 + A_j = 0$
. Expanding the above equation gives
Given another
![]() $4 \times 4$
skew-symmetric matrix
$4 \times 4$
skew-symmetric matrix
![]() $B$
whose eigenvalues are
$B$
whose eigenvalues are
![]() $\{\pm \phi _1 i, \pm \phi _2 i\}$
and
$\{\pm \phi _1 i, \pm \phi _2 i\}$
and
![]() $\phi _1 \geq \phi _2 \geq 0$
, we have
$\phi _1 \geq \phi _2 \geq 0$
, we have
where
![]() $C=P^{\intercal } B P$
. Notice
$C=P^{\intercal } B P$
. Notice
so
![]() $C$
is a skew-symmetric matrix as well, and
$C$
is a skew-symmetric matrix as well, and
![]() $C$
has exactly the same eigenvalues as
$C$
has exactly the same eigenvalues as
![]() $B$
since conjugation does not change the eigenvalues of a matrix. A similar conclusion can be drawn:
$B$
since conjugation does not change the eigenvalues of a matrix. A similar conclusion can be drawn:
 \begin{equation} \begin{split} & \textrm{trace} \left (\exp{A}\exp{B} \right ) = \textrm{trace} \left (\exp{\Omega _A}\exp{C} \right ) = \\ & =\textrm{trace}\left (\left (I + \sum _{i=1}^2 \left (\sin{\theta _i}\Omega _{i} + (1-\cos{\theta _i})\Omega _{i}^2 \right )\right ) \left (I + \sum _{i=1}^2 \left (\sin{\phi _i}C_i + (1-\cos{\phi _i})C_i^2 \right )\right )\right ) \\ & = \textrm{trace} \left (I+\sum _{i=1}^2 \left (\sin{\theta _i}\Omega _{i} + (1-\cos{\theta _i})\Omega _{i}^2 \right )+\sum _{i=1}^2 \left (\sin{\phi _i}C_i + (1-\cos{\phi _i})C_i^2 \right )\right ) \\ & + \textrm{trace}\left (\sum _{i=1}^2 \sum _{j=1}^2 \left (\sin{\theta _i}\Omega _{i} + (1-\cos{\theta _i})\Omega _{i}^2 \right ) \left (\sin{\phi _j}C_j + (1-\cos{\phi _j})C_j^2 \right )\right ). \end{split} \end{equation}
\begin{equation} \begin{split} & \textrm{trace} \left (\exp{A}\exp{B} \right ) = \textrm{trace} \left (\exp{\Omega _A}\exp{C} \right ) = \\ & =\textrm{trace}\left (\left (I + \sum _{i=1}^2 \left (\sin{\theta _i}\Omega _{i} + (1-\cos{\theta _i})\Omega _{i}^2 \right )\right ) \left (I + \sum _{i=1}^2 \left (\sin{\phi _i}C_i + (1-\cos{\phi _i})C_i^2 \right )\right )\right ) \\ & = \textrm{trace} \left (I+\sum _{i=1}^2 \left (\sin{\theta _i}\Omega _{i} + (1-\cos{\theta _i})\Omega _{i}^2 \right )+\sum _{i=1}^2 \left (\sin{\phi _i}C_i + (1-\cos{\phi _i})C_i^2 \right )\right ) \\ & + \textrm{trace}\left (\sum _{i=1}^2 \sum _{j=1}^2 \left (\sin{\theta _i}\Omega _{i} + (1-\cos{\theta _i})\Omega _{i}^2 \right ) \left (\sin{\phi _j}C_j + (1-\cos{\phi _j})C_j^2 \right )\right ). \end{split} \end{equation}
Divide
![]() $Q$
into
$Q$
into
![]() $2 \times 2$
blocks as follows:
$2 \times 2$
blocks as follows:
 \begin{equation} Q = \left [\begin{array}{cc|cc} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{21} & q_{22} & q_{23} & q_{24} \\ \hline q_{31} & q_{32} & q_{33} & q_{34} \\ q_{41} & q_{42} & q_{43} & q_{44} \\ \end{array}\right ] = \left [\begin{array}{cc} \boldsymbol{Q}_{11} & \boldsymbol{Q}_{12} \\ \boldsymbol{Q}_{21} & \boldsymbol{Q}_{22} \end{array} \right ], \end{equation}
\begin{equation} Q = \left [\begin{array}{cc|cc} q_{11} & q_{12} & q_{13} & q_{14} \\ q_{21} & q_{22} & q_{23} & q_{24} \\ \hline q_{31} & q_{32} & q_{33} & q_{34} \\ q_{41} & q_{42} & q_{43} & q_{44} \\ \end{array}\right ] = \left [\begin{array}{cc} \boldsymbol{Q}_{11} & \boldsymbol{Q}_{12} \\ \boldsymbol{Q}_{21} & \boldsymbol{Q}_{22} \end{array} \right ], \end{equation}
where
Denoting
![]() $\omega _{ij}=\det{\boldsymbol{Q}_{ij}}$
and
$\omega _{ij}=\det{\boldsymbol{Q}_{ij}}$
and
![]() $\varepsilon _{ij}=\|\boldsymbol{Q}_{ij}\|^2_{F}=q_{2i-1,2j-1}^2 + q_{2i-1,2j}^2 + q_{2i,2j-1}^2 + q_{2i,2j}^2$
, we have the following equities:
$\varepsilon _{ij}=\|\boldsymbol{Q}_{ij}\|^2_{F}=q_{2i-1,2j-1}^2 + q_{2i-1,2j}^2 + q_{2i,2j-1}^2 + q_{2i,2j}^2$
, we have the following equities:
 \begin{equation} \begin{split} & \textrm{trace}\left (\Omega _i C_j\right ) = \textrm{trace}\left (\Omega _i Q\Omega _i Q^{\intercal } \right ) = -2\omega _{ij} \\ & \textrm{trace}\left (\Omega _i^2 C_j^2\right ) = \textrm{trace}\left (\Omega _i^2 Q\Omega _i^2 Q^{\intercal } \right ) = \varepsilon _{ij}\\ & \textrm{trace}(C_i) = \textrm{trace}(Q\Omega _i Q^{\intercal }) = \textrm{trace}(\Omega _{i})=0 \\ & \textrm{trace}(C_i^2)= \textrm{trace}(Q\Omega _i^2 Q^{\intercal }) =\textrm{trace}(\Omega _{i}^2)=-2 \\ & \textrm{trace}\left (\Omega _{i}^2 C_j\right ) = \textrm{trace}\left (\Omega _{i} C_j^2\right ) = 0. \end{split} \end{equation}
\begin{equation} \begin{split} & \textrm{trace}\left (\Omega _i C_j\right ) = \textrm{trace}\left (\Omega _i Q\Omega _i Q^{\intercal } \right ) = -2\omega _{ij} \\ & \textrm{trace}\left (\Omega _i^2 C_j^2\right ) = \textrm{trace}\left (\Omega _i^2 Q\Omega _i^2 Q^{\intercal } \right ) = \varepsilon _{ij}\\ & \textrm{trace}(C_i) = \textrm{trace}(Q\Omega _i Q^{\intercal }) = \textrm{trace}(\Omega _{i})=0 \\ & \textrm{trace}(C_i^2)= \textrm{trace}(Q\Omega _i^2 Q^{\intercal }) =\textrm{trace}(\Omega _{i}^2)=-2 \\ & \textrm{trace}\left (\Omega _{i}^2 C_j\right ) = \textrm{trace}\left (\Omega _{i} C_j^2\right ) = 0. \end{split} \end{equation}
Combining (11) with (13) gives
 \begin{equation} \begin{split} & \textrm{trace} \left (\exp{A}\exp{B}\right ) = 4+ 2\sum _{i=1}^2\left (\cos{\theta _i}-1\right ) + 2\sum _{i=1}^2\left (\cos{\phi _i}-1\right ) \\ & \hspace{2.8cm} + \sum _{i=1}^2\sum _{j=1}^2 \left (-2\sin{\theta _i}\sin{\phi _j}\omega _{ij} + (1-\cos{\theta _i})(1-\cos{\phi _j})\varepsilon _{ij} \right ). \end{split} \end{equation}
\begin{equation} \begin{split} & \textrm{trace} \left (\exp{A}\exp{B}\right ) = 4+ 2\sum _{i=1}^2\left (\cos{\theta _i}-1\right ) + 2\sum _{i=1}^2\left (\cos{\phi _i}-1\right ) \\ & \hspace{2.8cm} + \sum _{i=1}^2\sum _{j=1}^2 \left (-2\sin{\theta _i}\sin{\phi _j}\omega _{ij} + (1-\cos{\theta _i})(1-\cos{\phi _j})\varepsilon _{ij} \right ). \end{split} \end{equation}
Using the fact
![]() $\varepsilon _{11}+\varepsilon _{12}=\varepsilon _{11}+\varepsilon _{21}=\varepsilon _{22}+\varepsilon _{12}=\varepsilon _{22}+\varepsilon _{21}=2$
as
$\varepsilon _{11}+\varepsilon _{12}=\varepsilon _{11}+\varepsilon _{21}=\varepsilon _{22}+\varepsilon _{12}=\varepsilon _{22}+\varepsilon _{21}=2$
as
![]() $Q$
is an orthogonal matrix, we can reduce (14) to
$Q$
is an orthogonal matrix, we can reduce (14) to
For convenience, in the following, we will use
![]() $L_1$
to denote
$L_1$
to denote
![]() $\textrm{trace} \left (\exp{A}\exp{B}\right )$
and
$\textrm{trace} \left (\exp{A}\exp{B}\right )$
and
![]() $L_2$
to denote
$L_2$
to denote
![]() $\textrm{trace} \left (\exp{(A+B)}\right )$
.
$\textrm{trace} \left (\exp{(A+B)}\right )$
.
Lemma 3.1. Let
![]() $\omega _{11} = \det{(\boldsymbol{Q_{11}})}, \omega _{12} = \det{(\boldsymbol{Q_{12}})}, \ \text{and} \ \varepsilon _{11}=\|\boldsymbol{Q}_{11}\|^2_{F}$
, where
$\omega _{11} = \det{(\boldsymbol{Q_{11}})}, \omega _{12} = \det{(\boldsymbol{Q_{12}})}, \ \text{and} \ \varepsilon _{11}=\|\boldsymbol{Q}_{11}\|^2_{F}$
, where
![]() $\boldsymbol{Q_{11}}$
and
$\boldsymbol{Q_{11}}$
and
![]() $\boldsymbol{Q_{12}}$
are defined as in (12), then the following equity holds
$\boldsymbol{Q_{12}}$
are defined as in (12), then the following equity holds
Proof.
Since
![]() $q_{11}q_{21}+q_{12}q_{22}+q_{13}q_{23}+q_{14}q_{24}=0$
(by orthogonality), we have
$q_{11}q_{21}+q_{12}q_{22}+q_{13}q_{23}+q_{14}q_{24}=0$
(by orthogonality), we have
that is,
Then,
 \begin{equation*} \begin {aligned} & \hspace {-0.7cm} RHS = 1 + \omega _{11}^2 - \omega _{12}^2 = 1 + (q_{11}q_{22}-q_{12}q_{21})^2 -(q_{13}q_{24}-q_{14}q_{23})^2 \\ & = 1 + q_{11}^2q_{22}^2 + q_{12}^2q_{21}^2 - q_{13}^2q_{24}^2 - q_{14}^2q_{23}^2 - 2q_{11}q_{12}q_{21}q_{22} + 2q_{13}q_{14}q_{23}q_{24} \\ & = 1 + q_{11}^2q_{22}^2+q_{12}^2q_{21}^2 - q_{13}^2q_{24}^2-q_{14}^2q_{23}^2 + q_{11}^2q_{21}^2 + q_{12}^2q_{22}^2 - q_{13}^2q_{23}^2 - q_{14}^2q_{24}^2\\ & = 1 + (q_{11}^2+q_{12}^2)(q_{21}^2+q_{22}^2) - (q_{13}^2+q_{14}^2)(q_{23}^2+q_{24}^2) \\ & = 1 + (q_{11}^2+q_{12}^2)(q_{21}^2+q_{22}^2) - (1-q_{11}^2-q_{12}^2)(1-q_{21}^2-q_{22}^2) \\ & = q_{11}^2+q_{12}^2 + q_{21}^2+q_{22}^2 = \varepsilon _{11} = LHS, \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} & \hspace {-0.7cm} RHS = 1 + \omega _{11}^2 - \omega _{12}^2 = 1 + (q_{11}q_{22}-q_{12}q_{21})^2 -(q_{13}q_{24}-q_{14}q_{23})^2 \\ & = 1 + q_{11}^2q_{22}^2 + q_{12}^2q_{21}^2 - q_{13}^2q_{24}^2 - q_{14}^2q_{23}^2 - 2q_{11}q_{12}q_{21}q_{22} + 2q_{13}q_{14}q_{23}q_{24} \\ & = 1 + q_{11}^2q_{22}^2+q_{12}^2q_{21}^2 - q_{13}^2q_{24}^2-q_{14}^2q_{23}^2 + q_{11}^2q_{21}^2 + q_{12}^2q_{22}^2 - q_{13}^2q_{23}^2 - q_{14}^2q_{24}^2\\ & = 1 + (q_{11}^2+q_{12}^2)(q_{21}^2+q_{22}^2) - (q_{13}^2+q_{14}^2)(q_{23}^2+q_{24}^2) \\ & = 1 + (q_{11}^2+q_{12}^2)(q_{21}^2+q_{22}^2) - (1-q_{11}^2-q_{12}^2)(1-q_{21}^2-q_{22}^2) \\ & = q_{11}^2+q_{12}^2 + q_{21}^2+q_{22}^2 = \varepsilon _{11} = LHS, \end {aligned} \end{equation*}
that is,
![]() $\varepsilon _{11} = 1 + \omega _{11}^2 - \omega _{12}^2$
.
$\varepsilon _{11} = 1 + \omega _{11}^2 - \omega _{12}^2$
.
Lemma 3.2. Let
![]() $\omega _{11}$
and
$\omega _{11}$
and
![]() $\omega _{12}$
be the determinants of
$\omega _{12}$
be the determinants of
![]() $\boldsymbol{Q_{11}}$
and
$\boldsymbol{Q_{11}}$
and
![]() $\boldsymbol{Q_{12}}$
, where
$\boldsymbol{Q_{12}}$
, where
![]() $\boldsymbol{Q_{11}}$
and
$\boldsymbol{Q_{11}}$
and
![]() $\boldsymbol{Q_{12}}$
are as defined in (12), then
$\boldsymbol{Q_{12}}$
are as defined in (12), then
![]() $|\omega _{11}+\omega _{12}| \leq 1$
and
$|\omega _{11}+\omega _{12}| \leq 1$
and
![]() $|\omega _{11}-\omega _{12}| \leq 1$
.
$|\omega _{11}-\omega _{12}| \leq 1$
.
Proof.
Since
![]() $\omega _{11} = q_{11}q_{22}-q_{12}q_{21}$
,
$\omega _{11} = q_{11}q_{22}-q_{12}q_{21}$
,
![]() $\omega _{12} = q_{13}q_{24}-q_{14}q_{23}$
,
$\omega _{12} = q_{13}q_{24}-q_{14}q_{23}$
,
![]() $q_{11}^2+q_{12}^2+q_{13}^2+q_{14}^2 = 1$
, and
$q_{11}^2+q_{12}^2+q_{13}^2+q_{14}^2 = 1$
, and
![]() $q_{21}^2+q_{22}^2+q_{23}^2+q_{24}^2 = 1$
, we have
$q_{21}^2+q_{22}^2+q_{23}^2+q_{24}^2 = 1$
, we have
 \begin{equation*} \begin {aligned} & (q_{11}^2+q_{12}^2+q_{13}^2+q_{14}^2)(q_{21}^2+q_{22}^2+q_{23}^2+q_{24}^2) - (\omega _{11}+\omega _{12})^2 \\ & = (q_{11}q_{21}+q_{12}q_{22})^2 + (q_{11}q_{23}+q_{14}q_{22})^2 + (q_{11}q_{24}-q_{13}q_{22})^2 \\ & + (q_{12}q_{23}-q_{14}q_{21})^2 + (q_{12}q_{24}+q_{13}q_{21})^2 + (q_{13}q_{23}+q_{14}q_{24})^2 \geq 0, \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} & (q_{11}^2+q_{12}^2+q_{13}^2+q_{14}^2)(q_{21}^2+q_{22}^2+q_{23}^2+q_{24}^2) - (\omega _{11}+\omega _{12})^2 \\ & = (q_{11}q_{21}+q_{12}q_{22})^2 + (q_{11}q_{23}+q_{14}q_{22})^2 + (q_{11}q_{24}-q_{13}q_{22})^2 \\ & + (q_{12}q_{23}-q_{14}q_{21})^2 + (q_{12}q_{24}+q_{13}q_{21})^2 + (q_{13}q_{23}+q_{14}q_{24})^2 \geq 0, \end {aligned} \end{equation*}
that is,
![]() $(\omega _{11}+\omega _{12})^2 \leq 1$
. The same deduction gives
$(\omega _{11}+\omega _{12})^2 \leq 1$
. The same deduction gives
![]() $(\omega _{11}-\omega _{12})^2 \leq 1$
.
$(\omega _{11}-\omega _{12})^2 \leq 1$
.
Let
Instantly by Lemma 3.2, we have
![]() $|m_1| \leq 1$
and
$|m_1| \leq 1$
and
![]() $|m_2| \leq 1$
. Recall that
$|m_2| \leq 1$
. Recall that
![]() $\varepsilon _{11} + \varepsilon _{12} = 2 = \varepsilon _{12} + \varepsilon _{22}$
, so
$\varepsilon _{11} + \varepsilon _{12} = 2 = \varepsilon _{12} + \varepsilon _{22}$
, so
![]() $\varepsilon _{11}=\varepsilon _{22}$
and similarly
$\varepsilon _{11}=\varepsilon _{22}$
and similarly
![]() $\varepsilon _{12}=\varepsilon _{21}$
. By Lemme 3.1, we have
$\varepsilon _{12}=\varepsilon _{21}$
. By Lemme 3.1, we have
and
Since
![]() $Q$
is an orthogonal matrix,
$Q$
is an orthogonal matrix,
![]() $\det Q = \pm 1$
which is denoted as
$\det Q = \pm 1$
which is denoted as
![]() $\mu$
. In ref. [Reference Hudson20], the author has shown that
$\mu$
. In ref. [Reference Hudson20], the author has shown that
and
if
![]() $Q$
is an orthogonal matrix. Therefore, we have
$Q$
is an orthogonal matrix. Therefore, we have
Substituting
![]() $\omega _{ij}$
and
$\omega _{ij}$
and
![]() $\varepsilon _{ij}$
with
$\varepsilon _{ij}$
with
![]() $m_1$
and
$m_1$
and
![]() $m_2$
into (15) gives
$m_2$
into (15) gives
 \begin{equation} \begin{split} & \hspace{-0.4cm} L_1 = (1+m_1m_2)\cos{\theta _1}\cos{\phi _1} + (1-m_1m_2)\cos{\theta _1}\cos{\phi _2} \\ & + (1-m_1m_2)\cos{\theta _2}\cos{\phi _1} + (1+m_1m_2)\cos{\theta _2}\cos{\phi _2} \\ & -(m_1+m_2)\sin{\theta _1}\sin{\phi _1} - (m_1-m_2)\sin{\theta _1}\sin{\phi _2} \\ & - \mu (m_1-m_2)\sin{\theta _2}\sin{\phi _1} - \mu (m_1+m_2)\sin{\theta _2}\sin{\phi _2}. \end{split} \end{equation}
\begin{equation} \begin{split} & \hspace{-0.4cm} L_1 = (1+m_1m_2)\cos{\theta _1}\cos{\phi _1} + (1-m_1m_2)\cos{\theta _1}\cos{\phi _2} \\ & + (1-m_1m_2)\cos{\theta _2}\cos{\phi _1} + (1+m_1m_2)\cos{\theta _2}\cos{\phi _2} \\ & -(m_1+m_2)\sin{\theta _1}\sin{\phi _1} - (m_1-m_2)\sin{\theta _1}\sin{\phi _2} \\ & - \mu (m_1-m_2)\sin{\theta _2}\sin{\phi _1} - \mu (m_1+m_2)\sin{\theta _2}\sin{\phi _2}. \end{split} \end{equation}
On the other hand,
Let
![]() $D =\Omega _A+C = \sum _{i=1}^2 \left ( \theta _i \Omega _i + \phi _i Q \Omega _i Q^{\intercal } \right )$
. The characteristic polynomial
$D =\Omega _A+C = \sum _{i=1}^2 \left ( \theta _i \Omega _i + \phi _i Q \Omega _i Q^{\intercal } \right )$
. The characteristic polynomial
![]() $\mathcal{P}(\lambda )$
of D is
$\mathcal{P}(\lambda )$
of D is
where
and
Using the face that
![]() $\omega _{22}=\mu \omega _{11}$
and
$\omega _{22}=\mu \omega _{11}$
and
![]() $\omega _{21}=\mu \omega _{12}$
, we can solve the above quartic equation:
$\omega _{21}=\mu \omega _{12}$
, we can solve the above quartic equation:
where
and
Both
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are guaranteed to be greater than or equal to
$f_2$
are guaranteed to be greater than or equal to
![]() $0$
since
$0$
since
![]() $|\omega _{11}+\omega _{12}| \leq 1$
,
$|\omega _{11}+\omega _{12}| \leq 1$
,
![]() $|\omega _{11}-\omega _{12}| \leq 1$
(Lemme 3.2),
$|\omega _{11}-\omega _{12}| \leq 1$
(Lemme 3.2),
![]() $\theta _1 \pm \mu \theta _2 \geq 0$
, and
$\theta _1 \pm \mu \theta _2 \geq 0$
, and
![]() $\phi _1 \pm \phi _2 \geq 0$
. So, expanding (17) by (9) gives
$\phi _1 \pm \phi _2 \geq 0$
. So, expanding (17) by (9) gives
 \begin{equation} \begin{split} & L_2 = \textrm{trace}\left (I+\sin{\psi _1}D_1+(1-\cos{\psi _1})D_1^2 + \sin{\psi _2}D_2+(1-\cos{\psi _2})D_2^2 \right ) \\ & \hspace{0.4cm} = 4 + 2(\cos{\psi _1}-1) + 2(\cos{\psi _2}-1) = 2\cos{\psi _1} + 2\cos{\psi _2} \\ & \hspace{0.4cm} = 2\cos{\left (\frac{\sqrt{f_1}+\sqrt{f_2}}{2}\right )} + 2\cos{\left (\frac{\sqrt{f_1}-\sqrt{f_2}}{2}\right )} = 4\cos{\frac{\sqrt{f_1}}{2}}\cos{\frac{\sqrt{f_2}}{2}}. \end{split} \end{equation}
\begin{equation} \begin{split} & L_2 = \textrm{trace}\left (I+\sin{\psi _1}D_1+(1-\cos{\psi _1})D_1^2 + \sin{\psi _2}D_2+(1-\cos{\psi _2})D_2^2 \right ) \\ & \hspace{0.4cm} = 4 + 2(\cos{\psi _1}-1) + 2(\cos{\psi _2}-1) = 2\cos{\psi _1} + 2\cos{\psi _2} \\ & \hspace{0.4cm} = 2\cos{\left (\frac{\sqrt{f_1}+\sqrt{f_2}}{2}\right )} + 2\cos{\left (\frac{\sqrt{f_1}-\sqrt{f_2}}{2}\right )} = 4\cos{\frac{\sqrt{f_1}}{2}}\cos{\frac{\sqrt{f_2}}{2}}. \end{split} \end{equation}
Perform the following coordinate transformations:
 \begin{equation*} \left [\begin {array}{c} x_1 \\ x_2 \\ y_1 \\ y_2 \\ \end {array} \right ] = \left [\begin {array}{cccc} 0.5 & 0.5\mu & 0.5 & 0.5 \\ 0.5 & -0.5\mu & 0.5 & -0.5 \\ -0.5 & -0.5\mu & 0.5 & 0.5 \\ -0.5 & 0.5\mu & 0.5 & -0.5 \end {array} \right ] \left [\begin {array}{c} \theta _1 \\ \theta _2 \\ \phi _1 \\ \phi _2 \\ \end {array} \right ]. \end{equation*}
\begin{equation*} \left [\begin {array}{c} x_1 \\ x_2 \\ y_1 \\ y_2 \\ \end {array} \right ] = \left [\begin {array}{cccc} 0.5 & 0.5\mu & 0.5 & 0.5 \\ 0.5 & -0.5\mu & 0.5 & -0.5 \\ -0.5 & -0.5\mu & 0.5 & 0.5 \\ -0.5 & 0.5\mu & 0.5 & -0.5 \end {array} \right ] \left [\begin {array}{c} \theta _1 \\ \theta _2 \\ \phi _1 \\ \phi _2 \\ \end {array} \right ]. \end{equation*}
Applying the above transformation to (16) and (19) gives
and
where
and
Lemma 3.3. Let
![]() $a = \frac{K}{\sqrt{2(1+\zeta )}}$
and
$a = \frac{K}{\sqrt{2(1+\zeta )}}$
and
![]() $b = \frac{K}{\sqrt{2(1-\zeta )}}$
, where
$b = \frac{K}{\sqrt{2(1-\zeta )}}$
, where
![]() $\zeta \in (-1,1)$
and
$\zeta \in (-1,1)$
and
![]() $K \in (0,\pi ]$
. Then
$K \in (0,\pi ]$
. Then
Proof. Let
and the derivative of
![]() $f(p)$
is
$f(p)$
is
It is not difficult to conclude that
![]() $\frac{df}{dp} \gt 0$
when
$\frac{df}{dp} \gt 0$
when
![]() $p \in (0,\pi )$
; that is,
$p \in (0,\pi )$
; that is,
![]() $f(p)$
is strictly increasing as
$f(p)$
is strictly increasing as
![]() $p \in (0,\pi ]$
. Assume that there exists a
$p \in (0,\pi ]$
. Assume that there exists a
![]() $p_0$
such that
$p_0$
such that
![]() $f(p_0) \lt f(\frac{\pi }{2})$
, then
$f(p_0) \lt f(\frac{\pi }{2})$
, then
So if such
![]() $p_0$
exists, it must satisfy
$p_0$
exists, it must satisfy
![]() $p_0 \lt \frac{\pi }{2}$
, which means for any
$p_0 \lt \frac{\pi }{2}$
, which means for any
![]() $p\geq \frac{\pi }{2}$
, we have
$p\geq \frac{\pi }{2}$
, we have
Let
![]() $q=\sqrt{2(1+\zeta )} \in (0,2)$
, then
$q=\sqrt{2(1+\zeta )} \in (0,2)$
, then
![]() $\frac{1}{q} \gt \frac{1}{2}$
and
$\frac{1}{q} \gt \frac{1}{2}$
and
![]() $\frac{K}{2q} \gt \frac{K}{4}$
. If
$\frac{K}{2q} \gt \frac{K}{4}$
. If
![]() $\frac{K}{2q} \lt \frac{\pi }{2}$
, then
$\frac{K}{2q} \lt \frac{\pi }{2}$
, then
since
![]() $f$
is strictly increasing within that range. Otherwise if
$f$
is strictly increasing within that range. Otherwise if
![]() $\frac{K}{2q} \geq \frac{\pi }{2}$
, we have
$\frac{K}{2q} \geq \frac{\pi }{2}$
, we have
![]() $f\left (\frac{K}{2q}\right ) \gt f(\frac{\pi }{4})\geq f(\frac{K}{4})$
. In other words, the following inequality is always valid:
$f\left (\frac{K}{2q}\right ) \gt f(\frac{\pi }{4})\geq f(\frac{K}{4})$
. In other words, the following inequality is always valid:
Multiplying both sides by
![]() $\frac{K^2}{4}$
gives
$\frac{K^2}{4}$
gives
that is,
By letting
![]() $\zeta = -\zeta$
, we have
$\zeta = -\zeta$
, we have
Lemma 3.4. If
![]() $x\gt 0$
,
$x\gt 0$
,
![]() $y\gt 0$
,
$y\gt 0$
,
![]() $\zeta \in (-1,1)$
, and
$\zeta \in (-1,1)$
, and
![]() $K \in (0,\pi ]$
, then the only solution to the following equation is
$K \in (0,\pi ]$
, then the only solution to the following equation is
![]() $x=y=K/2$
$x=y=K/2$
Proof.
Let
![]() $h(x)=\frac{\sin x}{x}$
. Assume that there exists
$h(x)=\frac{\sin x}{x}$
. Assume that there exists
![]() $x_1 \gt x_2 \gt 0$
such that
$x_1 \gt x_2 \gt 0$
such that
![]() $h(x_1)=h(x_2)$
. The derivative of
$h(x_1)=h(x_2)$
. The derivative of
![]() $h(x)$
is
$h(x)$
is
When
![]() $x\in (0,\frac{\pi }{2}]$
,
$x\in (0,\frac{\pi }{2}]$
,
![]() $x\cos x - \sin x$
will always be smaller than 0; that is,
$x\cos x - \sin x$
will always be smaller than 0; that is,
![]() $h(x)$
is strictly decreasing. Therefore, to have
$h(x)$
is strictly decreasing. Therefore, to have
![]() $h(x_1)=h(x_2)$
,
$h(x_1)=h(x_2)$
,
![]() $x_1$
must be greater than
$x_1$
must be greater than
![]() $\frac{\pi }{2}$
. Assume
$\frac{\pi }{2}$
. Assume
![]() $x_2 \leq \frac{\pi }{2}$
, then
$x_2 \leq \frac{\pi }{2}$
, then
Thus, we have
which leads to
![]() $x_1 \leq \frac{\pi }{2}$
, contradicting what we previously stated. Thus, both
$x_1 \leq \frac{\pi }{2}$
, contradicting what we previously stated. Thus, both
![]() $x_1$
and
$x_1$
and
![]() $x_2$
need to be larger than
$x_2$
need to be larger than
![]() $\frac{\pi }{2}$
. However,
$\frac{\pi }{2}$
. However,
which causes a contradiction since
![]() $K \in (0,\pi ]$
.
$K \in (0,\pi ]$
.
Theorem 3.5. If
![]() $(1+\zeta ) x^2+(1-\zeta ) y^2=\frac{K^2}{2}, \zeta \in [-1,1], \ \operatorname{and} \ K \in [0,\pi ]$
, then
$(1+\zeta ) x^2+(1-\zeta ) y^2=\frac{K^2}{2}, \zeta \in [-1,1], \ \operatorname{and} \ K \in [0,\pi ]$
, then
Proof.
If
![]() $\zeta = 1$
, then
$\zeta = 1$
, then
![]() $x = \pm \frac{K}{2}$
. So,
$x = \pm \frac{K}{2}$
. So,
![]() $LHS = 2\cos{\left (\frac{K}{2} \right )} = RHS$
. Same for
$LHS = 2\cos{\left (\frac{K}{2} \right )} = RHS$
. Same for
![]() $\zeta = -1$
. If
$\zeta = -1$
. If
![]() $K = 0$
, then
$K = 0$
, then
![]() $x=y=0$
. So,
$x=y=0$
. So,
![]() $LHS = 0 = RHS$
. Now, let us restrict
$LHS = 0 = RHS$
. Now, let us restrict
![]() $\zeta \in (-1,1)$
and
$\zeta \in (-1,1)$
and
![]() $K \in (0,\pi ]$
. Let
$K \in (0,\pi ]$
. Let
and
To find the minimum of
![]() $f(x,y)$
subjected to the equality constraint
$f(x,y)$
subjected to the equality constraint
![]() $g(x,y)=0$
, we form the following Lagrangian function:
$g(x,y)=0$
, we form the following Lagrangian function:
where
![]() $\lambda$
is the Lagrange multiplier. Notice that
$\lambda$
is the Lagrange multiplier. Notice that
![]() $\mathcal{L}(\pm x,\pm y, \lambda )=f(\pm x,\pm y)+\lambda g(\pm x,\pm y)=f(x,y) + \lambda g(x,y) = \mathcal{L}(x,y,\lambda )$
. Thus, the Lagrangian function is symmetric about
$\mathcal{L}(\pm x,\pm y, \lambda )=f(\pm x,\pm y)+\lambda g(\pm x,\pm y)=f(x,y) + \lambda g(x,y) = \mathcal{L}(x,y,\lambda )$
. Thus, the Lagrangian function is symmetric about
![]() $x=0$
and
$x=0$
and
![]() $y=0$
. So, we only need to study how
$y=0$
. So, we only need to study how
![]() $\mathcal{L}(x,y,\lambda )$
behaves with
$\mathcal{L}(x,y,\lambda )$
behaves with
![]() $(x,y)\in [0,+\infty ) \times [0,+\infty )$
. To find stationary points of
$(x,y)\in [0,+\infty ) \times [0,+\infty )$
. To find stationary points of
![]() $\mathcal{L}$
, we have
$\mathcal{L}$
, we have
 \begin{equation*} \left \{\begin {array}{l} \frac {\partial \mathcal {L}}{\partial x}=[-(1+\zeta ) \sin x]+2 \lambda (1+\zeta ) x=0 \\ \frac {\partial \mathcal {L}}{\partial y}=[-(1-\zeta ) \sin y]+2 \lambda (1-\zeta ) y=0 \\ \frac {\partial \mathcal {L}}{\partial \lambda }=(1+\zeta ) x^2+(1-\zeta ) y^2-\frac {K^2}{2}=0 \end {array}\right .. \end{equation*}
\begin{equation*} \left \{\begin {array}{l} \frac {\partial \mathcal {L}}{\partial x}=[-(1+\zeta ) \sin x]+2 \lambda (1+\zeta ) x=0 \\ \frac {\partial \mathcal {L}}{\partial y}=[-(1-\zeta ) \sin y]+2 \lambda (1-\zeta ) y=0 \\ \frac {\partial \mathcal {L}}{\partial \lambda }=(1+\zeta ) x^2+(1-\zeta ) y^2-\frac {K^2}{2}=0 \end {array}\right .. \end{equation*}
We can readily obtain three sets of solutions to the above equation:
-
1.
 $x=0$
,
$x=0$
,
 $y=\sqrt{\frac{K^2}{2(1-\zeta )}}$
and
$y=\sqrt{\frac{K^2}{2(1-\zeta )}}$
and
 $\lambda =\frac{\sin y}{2y}$
;
$\lambda =\frac{\sin y}{2y}$
; -
2.
 $x=y$
,
$x=y$
,
 $x=y=\frac{K}{2}$
and
$x=y=\frac{K}{2}$
and
 $\lambda =\frac{\sin{\frac{K}{2}}}{K}$
;
$\lambda =\frac{\sin{\frac{K}{2}}}{K}$
; -
3.
 $y=0$
,
$y=0$
,
 $x=\sqrt{\frac{K^2}{2(1+\zeta )}}$
and
$x=\sqrt{\frac{K^2}{2(1+\zeta )}}$
and
 $\lambda =\frac{\sin x}{2x}$
.
$\lambda =\frac{\sin x}{2x}$
.
To have a fourth solution, we need to satisfy
and
However, by Lemma 3.4, we conclude that there are no other solutions. Substituting those solutions back into
![]() $f(x,y)$
gives
$f(x,y)$
gives
 \begin{equation*} \begin {aligned} &f\left (0, \sqrt {\frac {K^2}{2(1-\zeta )}}\right ) = (1-\zeta )\cos \left (\sqrt {\frac {K^2}{2(1-\zeta )}}\right ) + 1+\zeta - 2\cos \left (\frac {K}{2}\right ) \\ &f\left (\frac {K}{2},\frac {K}{2}\right ) = 2\cos \left (\frac {K}{2}\right ) - 2\cos \left (\frac {K}{2}\right ) = 0 \\ & f\left (\sqrt {\frac {K^2}{2(1+\zeta )}},0\right ) = (1+\zeta )\cos \left (\sqrt {\frac {K^2}{2(1+\zeta )}}\right ) + 1-\zeta - 2\cos \left (\frac {K}{2}\right ). \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} &f\left (0, \sqrt {\frac {K^2}{2(1-\zeta )}}\right ) = (1-\zeta )\cos \left (\sqrt {\frac {K^2}{2(1-\zeta )}}\right ) + 1+\zeta - 2\cos \left (\frac {K}{2}\right ) \\ &f\left (\frac {K}{2},\frac {K}{2}\right ) = 2\cos \left (\frac {K}{2}\right ) - 2\cos \left (\frac {K}{2}\right ) = 0 \\ & f\left (\sqrt {\frac {K^2}{2(1+\zeta )}},0\right ) = (1+\zeta )\cos \left (\sqrt {\frac {K^2}{2(1+\zeta )}}\right ) + 1-\zeta - 2\cos \left (\frac {K}{2}\right ). \end {aligned} \end{equation*}
By Lemma 3.3, we have
![]() $f\left (0, \sqrt{\frac{K^2}{2(1-\zeta )}}\right )\gt 0$
and
$f\left (0, \sqrt{\frac{K^2}{2(1-\zeta )}}\right )\gt 0$
and
![]() $f\left (\sqrt{\frac{K^2}{2(1+\zeta )}},0\right )\gt 0$
. Therefore, we can conclude that the global minimum for
$f\left (\sqrt{\frac{K^2}{2(1+\zeta )}},0\right )\gt 0$
. Therefore, we can conclude that the global minimum for
![]() $f(x,y)$
subjected to
$f(x,y)$
subjected to
![]() $g(x,y)=0$
is zero, that is,
$g(x,y)=0$
is zero, that is,
Now recall that
and
where
and
By (18), we know
where
![]() $\{\pm \psi _1i,\pm \psi _2i\}$
are eigenvalues of
$\{\pm \psi _1i,\pm \psi _2i\}$
are eigenvalues of
![]() $A+B$
. With the condition
$A+B$
. With the condition
![]() $\psi _1 + \psi _2 \leq \pi$
, if
$\psi _1 + \psi _2 \leq \pi$
, if
![]() $K_1 \geq K_2$
, then
$K_1 \geq K_2$
, then
![]() $\psi _1 + \psi _2=K_1 \leq \pi$
and so
$\psi _1 + \psi _2=K_1 \leq \pi$
and so
![]() $K_2 \leq K_1 \leq \pi$
; otherwise if
$K_2 \leq K_1 \leq \pi$
; otherwise if
![]() $K_1 \lt K_2$
, then
$K_1 \lt K_2$
, then
![]() $\psi _1 + \psi _2=K_2 \leq \pi$
and
$\psi _1 + \psi _2=K_2 \leq \pi$
and
![]() $K_1 \lt K_2 \leq \pi$
. In both cases, we have
$K_1 \lt K_2 \leq \pi$
. In both cases, we have
![]() $K_1 \leq \pi$
and
$K_1 \leq \pi$
and
![]() $K_2 \leq \pi$
. By Theorem 3.5, we have
$K_2 \leq \pi$
. By Theorem 3.5, we have
and
Therefore, we have
![]() $L_1 \geq L_2$
, that is,
$L_1 \geq L_2$
, that is,
subjected to
3.2. 3D case
Given two
![]() $3 \times 3$
skew-symmetric matrices
$3 \times 3$
skew-symmetric matrices
![]() $A$
and
$A$
and
![]() $B$
such that the eigenvalues of
$B$
such that the eigenvalues of
![]() $A+B$
is
$A+B$
is
![]() $\{\pm \psi i, 0\}$
and
$\{\pm \psi i, 0\}$
and
![]() $\psi \in [0,\pi ]$
, we can pad both
$\psi \in [0,\pi ]$
, we can pad both
![]() $A$
and
$A$
and
![]() $B$
with zeros as follows:
$B$
with zeros as follows:
Then,
and
Notice that by padding zeros, the eigenvalues of
![]() $\bar{A}+\bar{B}$
become
$\bar{A}+\bar{B}$
become
![]() $\{\psi i,-\psi i,0,0\}$
. As
$\{\psi i,-\psi i,0,0\}$
. As
![]() $\psi + 0 = \psi \leq \pi$
, we have
$\psi + 0 = \psi \leq \pi$
, we have
that is,
4. Applications
In this section, two very different applications of the trace inequality are illustrated.
4.1. BCH formula
The Baker-Campbell-Hausdorff (BCH) formula gives the value of
![]() $\boldsymbol{Z}$
that solves the following equation:
$\boldsymbol{Z}$
that solves the following equation:
where
![]() $\boldsymbol{X},\boldsymbol{Y}, \text{and} \ \boldsymbol{Z}$
are in the Lie algebra of a Lie group,
$\boldsymbol{X},\boldsymbol{Y}, \text{and} \ \boldsymbol{Z}$
are in the Lie algebra of a Lie group,
![]() $[\boldsymbol{X},\boldsymbol{Y}] = \boldsymbol{X}\boldsymbol{Y}-\boldsymbol{Y}\boldsymbol{X}$
, and
$[\boldsymbol{X},\boldsymbol{Y}] = \boldsymbol{X}\boldsymbol{Y}-\boldsymbol{Y}\boldsymbol{X}$
, and
![]() $\cdots$
indicates terms involving higher commutators of
$\cdots$
indicates terms involving higher commutators of
![]() $\boldsymbol{X}$
and
$\boldsymbol{X}$
and
![]() $\boldsymbol{Y}$
. The BCH formula is used for robot state estimation [Reference Barfoot21] and error propagation on the Euclidean motion group [Reference Wang and Chirikjian22]. Let us denote all the terms after
$\boldsymbol{Y}$
. The BCH formula is used for robot state estimation [Reference Barfoot21] and error propagation on the Euclidean motion group [Reference Wang and Chirikjian22]. Let us denote all the terms after
![]() $\boldsymbol{X} + \boldsymbol{Y}$
as
$\boldsymbol{X} + \boldsymbol{Y}$
as
![]() $\boldsymbol{W}$
and so
$\boldsymbol{W}$
and so
Considering the case of
![]() $SO(3)$
, we can write
$SO(3)$
, we can write
where
![]() $\textbf{n}_i$
is the unit vector in the direction of the rotation axis,
$\textbf{n}_i$
is the unit vector in the direction of the rotation axis,
![]() $\hat{\textbf{n}}_i$
is the unique skew-symmetric matrix such that
$\hat{\textbf{n}}_i$
is the unique skew-symmetric matrix such that
for any
![]() $\textbf{v} \in \mathbb{R}^3$
, and
$\textbf{v} \in \mathbb{R}^3$
, and
![]() $\boldsymbol\theta _{\textbf{\textit{i}}} \boldsymbol\in \boldsymbol[\boldsymbol 0,\boldsymbol +\boldsymbol\infty \boldsymbol )$
is the angle of the rotation. Then,
$\boldsymbol\theta _{\textbf{\textit{i}}} \boldsymbol\in \boldsymbol[\boldsymbol 0,\boldsymbol +\boldsymbol\infty \boldsymbol )$
is the angle of the rotation. Then,
provided that
![]() $\|\theta _1 \textbf{n}_1 +\theta _2 \textbf{n}_2 \| \leq \pi$
. So, we conclude that the existence of
$\|\theta _1 \textbf{n}_1 +\theta _2 \textbf{n}_2 \| \leq \pi$
. So, we conclude that the existence of
![]() $\boldsymbol{W}$
will reduce the distance between
$\boldsymbol{W}$
will reduce the distance between
![]() $\exp (\boldsymbol{X}+\boldsymbol{Y})$
and the identity
$\exp (\boldsymbol{X}+\boldsymbol{Y})$
and the identity
![]() $\mathbb{I}_3$
if
$\mathbb{I}_3$
if
![]() $\|\theta _1 \textbf{n}_1 +\theta _2 \textbf{n}_2 \| \leq \pi$
.
$\|\theta _1 \textbf{n}_1 +\theta _2 \textbf{n}_2 \| \leq \pi$
.
4.2. Rotation fine-tuning
Euler angles are a powerful approach to decomposing rotation matrices into three sequential rotation matrices. Let us assume that a manipulator can rotate around the
![]() $x$
,
$x$
,
![]() $y$
, and
$y$
, and
![]() $z$
-axis, respectively. Therefore, to rotate the manipulator to a designated orientation
$z$
-axis, respectively. Therefore, to rotate the manipulator to a designated orientation
![]() $R_d$
, we can compute the corresponding Euler angles
$R_d$
, we can compute the corresponding Euler angles
![]() $\alpha _1$
,
$\alpha _1$
,
![]() $\beta _1$
, and
$\beta _1$
, and
![]() $\gamma _1$
such that
$\gamma _1$
such that
Assuming that whenever rotated, the device will incur some random noise to the input angle, that is,
leading to deviations of the final orientation. To reduce the error, one can measure the actual rotation
![]() $R_1$
and compute another set of Euler angles
$R_1$
and compute another set of Euler angles
![]() $\{\alpha _2,\beta _2,\gamma _2\}$
such that
$\{\alpha _2,\beta _2,\gamma _2\}$
such that
But inevitably, noise will again be introduced, and the actual rotation will become
Therefore, one can repeat the above process until
![]() $d(\prod _{i=1}^N R_{N-i+1}, R_d)$
is within tolerance. Another approach to reducing the inaccuracy caused by the noise is applying the following inequality:
$d(\prod _{i=1}^N R_{N-i+1}, R_d)$
is within tolerance. Another approach to reducing the inaccuracy caused by the noise is applying the following inequality:
To refine the current rotation by rotating the x-axis, that is, minimizing
![]() $d(R_x(\alpha )R_1, R_d) = \theta (R_x(\alpha )R_1R_d^T)$
, we let
$d(R_x(\alpha )R_1, R_d) = \theta (R_x(\alpha )R_1R_d^T)$
, we let
![]() $R_s = R_1R_d^T = \exp ({\theta _s\hat{\textbf{n}}_s})$
, where
$R_s = R_1R_d^T = \exp ({\theta _s\hat{\textbf{n}}_s})$
, where
![]() $\theta _s \in [0, \pi ]$
. If
$\theta _s \in [0, \pi ]$
. If
![]() $\alpha = \arg \min _{\alpha } \|\theta _s \textbf{n}_s +\alpha \textbf{e}_1 \|$
, that is,
$\alpha = \arg \min _{\alpha } \|\theta _s \textbf{n}_s +\alpha \textbf{e}_1 \|$
, that is,
![]() $\alpha = -(\textbf{n}_s \cdot \textbf{e}_1)\theta _s$
, then
$\alpha = -(\textbf{n}_s \cdot \textbf{e}_1)\theta _s$
, then
In other words, the inequality provides a simple way to reduce the angle of the resulting rotation by rotating around an axis with a specific angle. In practice, when given the
![]() $R_s$
, we compute
$R_s$
, we compute
![]() $|\textbf{n}_s \cdot \textbf{e}_1|$
,
$|\textbf{n}_s \cdot \textbf{e}_1|$
,
![]() $|\textbf{n}_s \cdot \textbf{e}_2|$
, and
$|\textbf{n}_s \cdot \textbf{e}_2|$
, and
![]() $|\textbf{n}_s \cdot \textbf{e}_3|$
and choose the axis that has the largest dot value to rotate. The above process is repeated until the tolerance requirement is met.
$|\textbf{n}_s \cdot \textbf{e}_3|$
and choose the axis that has the largest dot value to rotate. The above process is repeated until the tolerance requirement is met.

Figure 2. Average radian distance between the target rotation and the actual rotation.
To prove the effectiveness, we conduct the following experiment. The target rotation is chosen as
![]() $R_d = R_x(\alpha _*)R_y(\beta _*)R_z(\gamma _*)$
, where
$R_d = R_x(\alpha _*)R_y(\beta _*)R_z(\gamma _*)$
, where
![]() $\alpha _*$
,
$\alpha _*$
,
![]() $\beta _*$
, and
$\beta _*$
, and
![]() $\gamma _*$
are all random numbers from
$\gamma _*$
are all random numbers from
![]() $[0,2\pi ]$
. We assume that whenever the device is rotated, there will be a noise, which is uniformly distributed within the range
$[0,2\pi ]$
. We assume that whenever the device is rotated, there will be a noise, which is uniformly distributed within the range
![]() $[-0.15,0.15]$
, added to the input angle. In the first step, the manipulator is rotated according to the Euler angles for both methods. Then in the subsequent steps, it is refined three times either by Euler angles or by angles calculated from the inequality. For each approach, we refine the orientation to 100 steps, and at each step, the distance between the current rotation and the target rotation is measured. We conduct the above experiments 500 times, and the average distance is computed at each step for both approaches. The results are shown in Fig. 2. Overall, the radian distance is smaller if we refine the rotation by the inequality. In other words, the inequality provides a simple yet effective way to fine-tune the rotation in the presence of noise.
$[-0.15,0.15]$
, added to the input angle. In the first step, the manipulator is rotated according to the Euler angles for both methods. Then in the subsequent steps, it is refined three times either by Euler angles or by angles calculated from the inequality. For each approach, we refine the orientation to 100 steps, and at each step, the distance between the current rotation and the target rotation is measured. We conduct the above experiments 500 times, and the average distance is computed at each step for both approaches. The results are shown in Fig. 2. Overall, the radian distance is smaller if we refine the rotation by the inequality. In other words, the inequality provides a simple yet effective way to fine-tune the rotation in the presence of noise.
5. Conclusion
Kinematic metrics, that is, functions that measure the distance between two rigid-body displacements, are important in a number of applications in robotics ranging from inverse kinematics and mechanism design to sensor calibration. The triangle inequality is an essential feature of any distance metric. In this paper, it was shown how trace inequalities from statistical mechanics can be extended to the case of the Lie algebras
![]() $so(3)$
and
$so(3)$
and
![]() $so(4)$
and how these are in turn related to the triangle inequality for metrics on the Lie groups
$so(4)$
and how these are in turn related to the triangle inequality for metrics on the Lie groups
![]() $SO(3)$
and
$SO(3)$
and
![]() $SO(4)$
. These previously unknown relationships may shed a new light on kinematic metrics for use in robotics.
$SO(4)$
. These previously unknown relationships may shed a new light on kinematic metrics for use in robotics.
Author contributions
Dr. Gregory Chirikjian made the conjecture that the trace inequality can be extended to the case of the Lie algebras
![]() $so(3)$
and
$so(3)$
and
![]() $so(4)$
and proposed several potential applications. Yuwei Wu proved the conjecture. Both authors contributed to writing the article.
$so(4)$
and proposed several potential applications. Yuwei Wu proved the conjecture. Both authors contributed to writing the article.
Financial support
This work was supported by NUS Startup grants A-0009059-02-00 and A-0009059-03-00, CDE Board Fund E-465-00-0009-01, and AME Programmatic Fund Project MARIO A-0008449-01-00.
Competing interests
The authors declare no conflicts of interest exist.