Hostname: page-component-5cf477f64f-r2nwp Total loading time: 0 Render date: 2025-03-31T06:51:43.664Z Has data issue: false hasContentIssue false
  • English
  • Français

Task priority-based redundancy resolution of a 20 DoFs humanoid robot for object pick and place with minimum energy and dynamic balance

Published online by Cambridge University Press:  28 March 2025

James Sorokhaibam Open the ORCID record for James Sorokhaibam [Opens in a new window]  and
Ashish Dutta Open the ORCID record for Ashish Dutta [Opens in a new window]
James Sorokhaibam*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kanpur, Kanpur, Uttar Pradesh, India
Ashish Dutta
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kanpur, Kanpur, Uttar Pradesh, India
*
Corresponding author: James Sorokhaibam; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Humanoid robots are highly redundant, and finding whole-body optimal trajectories for various tasks is very complex. This paper proposes a method to find an energy-optimal, dynamically balanced, and collision-free trajectory of the 20 degrees of freedom humanoid robot in pick and place application. The task of pick and place is divided into three subtasks using the Pseudoinverse Jacobian method of redundancy resolution. The three subtasks are end effector trajectory represented by 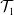$\mathcal {T}_1$, hip trajectory represented by 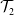$\mathcal {T}_2$, and maximizing the manipulability represented by 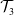$\mathcal {T}_3$. The Pseudoinverse Jacobian method is coupled with particle swarm optimization (PSO) to find the optimal trajectories. The main contribution of this paper is the decomposition of the whole-body task of the humanoid robot into three distinct subtasks to find energy-optimal, dynamically balanced, and obstacle-free trajectories. The concept of virtual surface is used to avoid dragging objects on the table surface. The problem is optimized with Particle Swarm Optimization. Simulations were conducted to pick up and place objects from a table and constrained spaces like a drawer. The results show that the robot can pick and place objects from defined locations on the table.

Keywords

humanoid robotsredundant manipulatorsrobot dynamicsmotion planning
Type
Research Article
Information
Robotica , First View , pp. 1 - 17
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Kuffner, J. J., Kagami, S., Nishiwaki, K., Inaba, M. and Inoue, H., “Dynamically-stable motion planning for humanoid robots,” Auton. Robot 12(1), 105–118 (2002).Google Scholar
Dalibard, S., Nakhaei, A., Lamiraux, F. and Laumond, J.-P., “Whole-body task planning for a humanoid robot: a way to integrate collision avoidance,” article-9th IEEE-RAS International Conference on Humanoid Robots, (Paris, France, IEEE, 2009) pp. 355–360.CrossRefGoogle Scholar
Teja, K. H., James, F. and Shah, S. V., “Optimal whole body motion planning of humanoid with articulated spine for object manipulation in double support phase,” Proceedings of the 2015 Conference on Advances in Robotics, (Goa, India, ACM, 2015) pp. 1–6.CrossRefGoogle Scholar
K., H. T., Balachandran, A. and Shah, S. V., “Optimal whole-body motion planning of humanoids in cluttered environments,” Robot. Auton. Syst. 118, 263–277 (2019). doi:10.1016/j.robot.2019.04.004.Google Scholar
Ruchanurucks, M., “Humanoid robot upper body motion generation using B-spline-based functions,” Robotica 33(4), 705–720 (2015).Google Scholar
Yu, L., Zhou, S. and Huang, S., “Trajectory optimization of the redundant manipulator with local variable period under multi-machine coordination,” Robotica 41(1), 292–305 (2023).CrossRefGoogle Scholar
Nakamura, Y., Hanafusa, H. and Yoshikawa, T., “Task-priority based redundancy control of robot manipulators,” Int. J. Rob. Res. 6(2), 3–15 (1987).Google Scholar
Ott, C., Dietrich, A. and Albu-Schäffer, A., “Prioritized multi-task compliance control of redundant manipulators,” Automatica 53, 416–423 (2015).Google Scholar
Gams, A., Van den Kieboom, J., Dzeladini, F., Ude, A. and Ijspeert, A. J., “Real-time full body motion imitation on the COMAN humanoid robot,” Robotica 33(5), 1049–1061 (2015).CrossRefGoogle Scholar
Karimi, M. and Ahmadi, M., “A reinforcement learning approach in assignment of task priorities in kinematic control of redundant robots,” IEEE Robot. Autom. Lett. 7(2), 850–857 (2021).Google Scholar
Liu, Z., Huang, Y., Liu, D., Guo, X., Wang, K. and Tan, J., “Trajectory planning of large redundant manipulator considering kinematic constraints and energy efficiency,” Robotica 41(11), 3524–3540 (2023).Google Scholar
Tomić, M., Chevallereau, C., Jovanović, K., Potkonjak, V. and Rodić, A., “Human to humanoid motion conversion for dual-arm manipulation tasks,” Robotica 36(8), 1167–1187 (2018).Google Scholar
Quan, Y., Wang, K., Zhao, C., Lv, C., Zhao, H. and Lv, H., “Obstacle avoidance method for fixed trajectory of a seven-degree-of-freedom manipulator,” Robotica 41(5), 1515–1535 (2023).Google Scholar
Zacharia, P. T. and Xidias, E. K., “Optimal robot task scheduling in cluttered environments considering mechanical advantage,” Robotica 42(9), 1–17 (2024).CrossRefGoogle Scholar
Zhao, J. and Wei, Y., “A novel algorithm of human-like motion planning for robotic arms,” Int. J. HR 14(01), 1650023 (2017).Google Scholar
Hammam, G. B., Wensing, P. M., Dariush, B. and Orin, D. E., “Kinodynamically consistent motion retargeting for humanoids,” Int. J. HR 12(04), 1550017 (2015).Google Scholar
Zhang, F., Qu, J., Liu, H. and Fu, Y., “A multi-priority control of asymmetric coordination for redundant dual-arm robot,” Int. J. HR 16(02), 1950008 (2019).Google Scholar
Jeong, J. W. and Chang, P. H., “A task-priority based framework for multiple tasks in highly redundant robots,” 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, (St. Louis, MO, USA, IEEE, 2009) pp. 5886–5891.CrossRefGoogle Scholar
Tsuichihara, S., Hakamata, Y., Ricardez, G. A. G., Takamatsu, J. and Ogasawara, T., “Accelerating whole-body motion generation using regression of the torso posture of a humanoid robot,” 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), (Cancun, Mexico, IEEE, 2016) pp. 16–21.CrossRefGoogle Scholar
Sentis, L. and Khatib, O., “A whole-body control framework for humanoids operating in human environments,” Proceedings 2006 IEEE International Conference on Robotics and Automation, (Orlando, FL, USA, IEEE, 2006) pp. 2641–2648.CrossRefGoogle Scholar
Acar, C. and Murakami, T., “Multi-task control for dynamically balanced two-wheeled mobile manipulator through task-priority,” 2011 IEEE International Symposium on Industrial Electronics, (Gdansk, Poland, IEEE, 2011) pp. 2195–2200.CrossRefGoogle Scholar
Tsuichihara, S., Yamaguchi, A., Takamatsu, J. and Ogasawara, T., “Using a weighted pseudo-inverse matrix to generate upper body motion for a humanoid robot doing household tasks,” 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), (Zhuhai, China, IEEE, 2015) pp. 333–338.CrossRefGoogle Scholar
Sugiura, H., Gienger, M., JANßEN, H. and Goerick, C., “Reactive self collision avoidance with dynamic task prioritization for humanoid robots,” Int. J. HR 7(01), 31–54 (2010).Google Scholar
Kang, P., Meng, H. and Xu, W., “A unified modeling and trajectory planning method based on system manipulability for the operation process of the legged locomotion manipulation system,” Robotica 41(7), 2139–2154 (2023).Google Scholar
Vukobratović, M. and Borovac, B., “Zero-moment point—thirty five years of its life,” Int. J. HR 1(01), 157–173 (2004).Google Scholar
Yoshikawa, T.. Foundations of Robotics: Analysis and Control (MIT Press, Cambridge, Massachusetts, 1990).Google Scholar
Witney, D. E., “The mathematics of coordinated control of prosthetic arms and manipulators,” J. Dyn. Sys., Meas., Control 94(4), 303--309 (1972).CrossRefGoogle Scholar
Craig, J. J., “Introduction to robotics: Mechanics and control”, (3/E. Pearson EducationIndia, 2009).Google Scholar
Sardain, P. and Bessonnet, G., “Forces acting on a biped robot. center of pressure-zero moment point,” IEEE Trans. Syst. Man Cybern. A Syst. Hum. 34(5), 630–637 (2004).Google Scholar