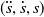1. Introduction
A machine possesses a kinematic and a dynamic structure, so does the process. One art of engineering consists in matching both as optimally as possible. Physics and mathematics of mechanics can help, and this is the goal of the paper. To give an example: The problem of trajectory planning for robotic systems is well known from the beginning of robotic research during the seventies and eighties. Especially, one approach has been particularly successful at that time. It represents a prescribed path by one degree of freedom (DOF) only, namely the curvilinear coordinate s along that path. All robot DOFs were then projected to this single path coordinate coming out with a linear system of ordinary differential equations of motion in the square of the path velocity. Many large applications and comparisons with measurements were carried through at that time [Reference Pfeiffer1–Reference Dubowsky and Shiller6]. The original idea for such an approach, by the way, comes from military research, being obvious.
In traditional mechanism theory and related fields, we find also many applications using mathematical concepts with very similar properties. It is possibly the first area trying from the very beginning to find a synthesis for more and more complicated mechanisms of plane and spatial nature, and it has been mainly represented by many scientists of a very high standing community [Reference Angeles7–Reference Wittenburg9], to name a few.
By analyzing various types of processes, we shall find an astonishingly large number of processes being defined by a trajectory only, from manufacturing and transport technologies to trajectory realization of robots. Therefore, the one-dimensional robot example includes a certain amount of generality. In addition, this idea might be generalized by considering processes with more than one DOF, which means multiple trajectories. We shall not pursue that here.
We may look to this step from the machine to the process or vice versa also in another way of arguing. Forcing a machine to perform a certain process, and the machine can do that only by a correspondingly good arrangement of its own constraints, means nothing else, that the contact element of that machine with the external world must follow the prescribed process kinematics and possibly some forces necessary for the process. A gripper of a robot follows a given path for example, or it performs a peg-in-hole process, as perfectly as possible. This is nothing else than running some additional constraints characterizing the process, in our case some path tracking.
2. Equations of Motion
Usually, kinematics and possibly some forces of a robot process are known, and the dynamics is unknown. This requires a multibody-dynamical model of the robot with the necessity, that all components follow the prescribed path or process. We start with possible models for the robot. In a first step and for later definitions, we consider Jourdain’s principle of lost power for a rigid multibody system [Reference Pfeiffer2, Reference Bremer10–Reference Woernle12].
\begin{align} \sum _{i=1}^{n} \delta \underbrace{\begin{pmatrix}{\mathbf{v}}_{O'} \\ \\[-9pt] \mathbf{\omega } \end{pmatrix}}_{\dot{\mathbf{z}}^T} \Biggl \lbrace \frac{d}{dt} \underbrace{\biggl [ \begin{pmatrix} m\mathbf{I} &\quad m \tilde{\mathbf{r}}_{O'S}^{T} \\ \\[-9pt] m \tilde{\mathbf{r}}_{O'S} &\quad \mathbf{\Theta }_{O'} \end{pmatrix}}_{\mathbf{M}} \underbrace{\begin{pmatrix}{\mathbf{v}}_{O'} \\ \\[-9pt] \mathbf{\omega } \end{pmatrix}}_{\dot{\mathbf{z}}} \biggr ] + \underbrace{\begin{pmatrix} m \tilde{\mathbf{\omega }} \tilde{\mathbf{\omega }} \mathbf{r}_{O'S} \\ \\[-9pt] \tilde{\mathbf{\omega }} \mathbf{\Theta }_{O'} \mathbf{\omega } \end{pmatrix}}_{\mathbf{f}^{g}} - \underbrace{\begin{pmatrix} \mathbf{F}^{e}+\mathbf{F}^{a}+\mathbf{F}^{p} \\ \\[-9pt] \mathbf{M}^{e}_{O'}+\mathbf{M}^{a}_{O'}+\mathbf{M}^{p}_{O'} \end{pmatrix}}_{\mathbf{f}^{e}+\mathbf{f}^{a}+\mathbf{f}^{p}} - \underbrace{\begin{pmatrix} \mathbf{F}^{c} \\ \\[-9pt] \mathbf{M}^{c}_{O'} \end{pmatrix}}_{\mathbf{f}^{c}} \Biggl \rbrace _{i} = \mathbf{0}. \end{align}
where
$\mathbf{v}_{O'}, \mathbf{\omega }$
are the translational and rotational velocities;
$m, \mathbf{I}, \mathbf{\Theta }_{O'}$
are the masses and mass moments of inertia;
$O^{\prime },S$
are the reference point and center of gravity; and
$\mathbf{f}^{g}, \mathbf{f}^{e}, \mathbf{f}^{a}, \mathbf{f}^{p}, \mathbf{f}^{c}$
are the gyroscopic, applied, driving, process, and constraint forces and torques. We have included also the case of a time-dependent mass matrix, which appears for rigid reference frames.
Equation (1) is defined in a
$\Re ^{6}$
-space for each component, for n components in a
$\Re ^{6n}$
-space. With
\begin{align} \mathbf{z} \,{:\!=}\, \begin{pmatrix} \mathbf{z}_{1} \\ \vdots \\ \mathbf{z}_{n} \end{pmatrix}, \qquad \quad \mathbf{f}^{g} \,{:\!=}\, \begin{pmatrix} \mathbf{f}^{g}_{1} \\ \vdots \\ \mathbf{f}^{g}_{n} \end{pmatrix}, \qquad \mathbf{f}^{e} \,{:\!=}\, \begin{pmatrix} \mathbf{f}_{1}^{e} \\ \vdots \\ \mathbf{f}_{n}^{e} \end{pmatrix}, \qquad \mathbf{f}^{a} \,{:\!=}\, \begin{pmatrix} \mathbf{f}_{1}^{a} \\ \vdots \\ \mathbf{f}_{n}^{a} \end{pmatrix}, \qquad \mathbf{f}^{p} \,{:\!=}\, \begin{pmatrix} \mathbf{f}_{1}^{p} \\ \vdots \\ \mathbf{f}_{n}^{p} \end{pmatrix}, \end{align}
we come to the corresponding vectors in the
$\Re ^{6n}$
-space (
$n=n_c$
number of components), and with
\begin{align} \mathbf{M} \,{:\! =}\, \textrm{diag} \left ( \mathbf{M}_{i} \right ) \in \Re ^{6n,6n} \end{align}
we define the mass matrix of the total system. From this, Eq. (1) takes on the form
\begin{align} \delta \dot{\mathbf{z}}^{T} \left ( \mathbf{M} \ddot{\mathbf{z}} + \dot{\mathbf{M}} \dot{\mathbf{z}} + \mathbf{f}^{g} - \mathbf{f}^{e} - \mathbf{f}^{a} - \mathbf{f}^{p} - \mathbf{f}^{c} \right ) = 0 \;. \end{align}
The virtual velocities
$\delta \dot{\mathbf{z}}$
cannot be chosen arbitrarily, but they must satisfy side conditions in the form of constraints, usually given by (
$\dot{\mathbf{\Phi }} = \mathbf{W}^T \dot{\mathbf{z}} + \bar{\mathbf{w}} = \mathbf{0}$
) [Reference Bremer10]. The
$\mathbf{W}$
-matrices are Jacobians defining the tangential constraint surfaces. The constraint forces are perpendicular to these manifolds. All constraints are assumed to be bilateral and independent from each other. For a classification of constraints, see, for example, refs. [Reference Pfeiffer2, Reference Bremer10].
Following the ideas of Jacobi [Reference Jacobi11] in the form given in ref. [Reference Bremer10], we come out finally with the typical structure of classical multibody equations with constraints
\begin{align} &\mathbf{M}\ddot{\mathbf{z}} + \dot{\mathbf{M}} \dot{\mathbf{z}} + \mathbf{f} - \mathbf{f}^{c} = \mathbf{0}, \qquad \mathbf{f} = \mathbf{f}^{g} - \mathbf{f}^{e} - \mathbf{f}^{a} - \mathbf{f}^{p}, \qquad \mathbf{f}^{c} = -\mathbf{W}(\mathbf{z},t) \mathbf{\lambda }, \nonumber \\ &\dot{\mathbf{\Phi }} = \mathbf{W}^T \dot{\mathbf{z}} + \bar{\mathbf{w}} = \mathbf{0}, \qquad \ddot{\mathbf{\Phi }} = \mathbf{W}^T \ddot{\mathbf{z}} + \left[\left(\frac{d\mathbf{W}^T}{dt}\right) \dot{\mathbf{z}} + \left(\frac{d \bar{\mathbf{w}}}{dt}\right)\right] = \mathbf{W}^T \ddot{\mathbf{z}} + \hat{\mathbf{w}} = \mathbf{0}, \quad \end{align}
The mass matrix is positive definite and symmetric. The vector
$\bar{\mathbf{w}}$
might be time-dependent elements of a constraint structure, see, for example, Eqs. (32)−(34). The constraints
$\dot{\mathbf{\Phi }}$
include robot and path constraints
$\mathbf{\Phi }$
. The equations above may be solved using
\begin{align} \begin{pmatrix}\mathbf{M} &\quad \mathbf{W}\\ \\[-8pt]\mathbf{W}^T &\quad \mathbf{0}\end{pmatrix}\begin{pmatrix}\ddot{\mathbf{z}}\\ \\[-8pt]\mathbf{\lambda }\end{pmatrix} + \begin{pmatrix} \dot{\mathbf{M}} \dot{\mathbf{z}}+\mathbf{f}\\ \\[-8pt] \hat{\mathbf{w}}\end{pmatrix} = \begin{pmatrix}\mathbf{0}\\ \\[-8pt] \mathbf{0}\end{pmatrix} \;. \end{align}
or evaluated
\begin{align} \ddot{\mathbf{z}} =& - \mathbf{M}^{-1} \left [(\dot{\mathbf{M}} \dot{\mathbf{z}}+\mathbf{f})+ \mathbf{W} (\mathbf{W}^T{\mathbf{M}}^{-1} \mathbf{W})^{-1} \mathbf{W}^T\mathbf{M}^{-1} [(\dot{\mathbf{M}} \dot{\mathbf{z}}+\mathbf{f}) - \hat{\mathbf{w}}] \right ], \nonumber \\[3pt] \mathbf{\lambda } =& -(\mathbf{W}^T{\mathbf{M}}^{-1} \mathbf{W})^{-1} \left [ \mathbf{W}^T\mathbf{M}^{-1} (\dot{\mathbf{M}} \dot{\mathbf{z}}+\mathbf{f}) - \hat{\mathbf{w}} \right ]. \end{align}
Due to the special requirements of dealing with multibody systems, many bodies forming a system like a machine, it makes sense to work with body-fixed coordinates and inertial ones. They are connected by a set of transformations, which have to be defined. For our robot case, it will be given in the following sections [Reference Pfeiffer2, Reference Woernle12].
Furthermore, we shall use a convenient property of the above relations. If the coordinate
$\mathbf{z}$
depends on some other coordinates
$\mathbf{q}$
, where
$\mathbf{z}$
might be non-minimal and
$\mathbf{q}$
might be minimal, then from ref. [Reference Bremer10]
\begin{align} \dot{\mathbf{\Phi }} = \mathbf{W}^T \dot{\mathbf{z}} + \bar{\mathbf{w}} = \mathbf{W}^T \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right) \dot{\mathbf{q}} + \bar{\mathbf{w}} = \mathbf{0}, \qquad \quad \frac{\partial \dot{\mathbf{\Phi }}}{\partial \dot{\mathbf{q}}} = \mathbf{W}^T \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right) = \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T \mathbf{W} = \mathbf{0}, \end{align}
which is helpful for eliminating the constraint force
$\mathbf{f}^{c} = -\mathbf{W}(\mathbf{z},t) \mathbf{\lambda }$
from the equations of motion, by pre-multiplying with
$(\frac{\partial \mathbf{z}}{\partial \mathbf{q}})^T$
. This is nothing else than a projection into the tangential planes as spanned by the constraints, characterized by free motion and no constraints anymore. Considering that case
$[\mathbf{z} = \mathbf{z}(\mathbf{q})]$
in more detail and applying Eqs. (8) to (5) gives with (
$\mathbf{M}_q = [(\frac{\partial \mathbf{z}}{\partial \mathbf{q}})^T \mathbf{M} (\frac{\partial \mathbf{z}}{\partial \mathbf{q}})]$
)
\begin{equation} \mathbf{M}_q \ddot{\mathbf{q}} + \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T \biggl \lbrace \mathbf{M} \biggl[ \frac{\partial }{\partial \mathbf{q}} \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right) \dot{\mathbf{q}} \biggr] \dot{\mathbf{q}} + [(\frac{\partial \mathbf{M}}{\partial \mathbf{q}})\dot{\mathbf{q}}](\frac{\partial \mathbf{z}}{\partial \mathbf{q}})\dot{\mathbf{q}} \biggr \rbrace + \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T \left(\mathbf{f}^{g} - \mathbf{f}^{e} - \mathbf{f}^{a} - \mathbf{f}^{p}\right) = \mathbf{0}, \end{equation}
If
$\mathbf{q}$
are robot coordinates, they depend on the path coordinates s, (
$\mathbf{q} = \mathbf{q}(s)$
). Considering in addition
\begin{align} \dot{\mathbf{q}} = \left(\frac{\partial \mathbf{q}}{\partial s}\right) \dot{s} = \mathbf{q}^{\prime } \dot{s}, \qquad \quad \ddot{\mathbf{q}} &= \left(\frac{d \dot{\mathbf{q}}}{d t}\right) = \frac{d }{d s} \left(\frac{\partial \mathbf{q}}{\partial s}\right) \dot{s}^2 + \left(\frac{\partial \mathbf{q}}{\partial s}\right) \ddot{s} = \mathbf{q}^{\prime \prime } \dot{s}^2 + \mathbf{q}^{\prime } \ddot{s}, \nonumber \\[3pt] \ddot{s} &= \left(\frac{d \dot{s}}{d t}\right) = \left(\frac{\partial \dot{s}}{\partial s}\right) \dot{s} = \frac{1}{2} \left(\frac{\partial \dot{s}^2}{\partial s}\right) = \frac{1}{2} (\dot{s}^2)^{\prime } \end{align}
we get from (9) a set of ordinary differential equations linear in the square of the path velocity
$\dot{\mathbf{s}}^2$
, which can be organized in the following way:
\begin{align} & \mathbf{A}(s) (\dot{s}^2)^{\prime } + \mathbf{B}(s) (\dot{s}^2) + \mathbf{C}(s) = \mathbf{T}(s), \quad \qquad (\mathbf{A}, \mathbf{B}, \mathbf{C},\mathbf{T}) \in \Re ^{n_q}, \nonumber \\[3pt] & \mathbf{B}(s) = \mathbf{M}_q \mathbf{q}^{\prime \prime } + \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T \biggl \lbrace \mathbf{M} \biggl [ \frac{\partial }{\partial \mathbf{q}} (\frac{\partial \mathbf{z}}{\partial \mathbf{q}}) \mathbf{q}^{\prime } \biggr ] \mathbf{q}^{\prime } + \left[\left(\frac{\partial \mathbf{M}}{\partial \mathbf{q}}\right)\mathbf{q}^{\prime }\right]\left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)\mathbf{q}^{\prime } \biggr \rbrace, \nonumber \\[3pt] & \mathbf{A}(s) = \frac{1}{2} \mathbf{M}_q \mathbf{q}^{\prime }, \qquad \mathbf{C}(s) = \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T \mathbf{f}_q^{e}, \qquad \mathbf{T}(s) = \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T\mathbf{f}_q^{a}, \nonumber \\[3pt] & \mathbf{f}_{q} = \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T (\mathbf{f}^{g} - \mathbf{f}^{e} - \mathbf{f}^{a} - \mathbf{f}^{p})_q, \qquad \mathbf{f}_q^{g} = \mathbf{B}(s), \end{align}
These relations define straight lines in the plane
$(\dot{s}^2)^{\prime }, (\dot{s}^2)$
for each s = constant in such a way that every of the
$n_q$
equations describes two parallel lines for a maximum and a minimum value of the driving torques. Note that, due to using an inertial frame,
$\mathbf{f}_q^{g}$
corresponds to the coefficient
$\mathbf{B}(s)$
. Working with body-fixed frames, it must additionally be determined.
If we want in addition to evaluate the constraint forces or torques, we must go back to Eqs. (5) and (6), and we must define the constraints. With respect to these constraints, we might consider two possibilities: first, including all constraints concerning joints and ground contact, or second, including only the ground contact constraint. Last case is of interest, if the joint constraints are already known by a special solution step or if the joint constraints are not of interest. The equations presented in the following are for all constraints. They write
\begin{align} & \mathbf{f}^c = - \mathbf{W} \mathbf{\lambda } \quad \Longrightarrow \quad \mathbf{f}^c + \mathbf{\beta }(s) (\dot{s}^2) + \mathbf{\gamma }(s) = \mathbf{\tau }(s), \qquad \quad \left(\mathbf{\beta }, \mathbf{\gamma }, \mathbf{\tau }\right) \in \Re ^{6n_c}, \nonumber \\ & \mathbf{\beta }(s) = +\mathbf{W} \left(\mathbf{W}^T \mathbf{M}_q^{-1} \mathbf{W}\right)^{-1} \left \lbrace \mathbf{W}^T \mathbf{M}_q^{-1}\left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T\left[\mathbf{M}_m \left(\frac{\partial }{\partial \mathbf{q}} \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right) \mathbf{q}^{\prime }\right) \mathbf{q}^{\prime } + \left(\frac{\partial \mathbf{M}_m}{\partial \mathbf{q}}\right)\mathbf{q}^{\prime }\left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)\mathbf{q}^{\prime }\right] - \hat{\mathbf{w}} \right\rbrace, \nonumber \\ & \mathbf{\gamma }(s) = -\mathbf{W} \left(\mathbf{W}^T \mathbf{M}_q^{-1} \mathbf{W}\right)^{-1} \mathbf{W}^T \mathbf{M}_q^{-1} \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T \left(\mathbf{f}^{e} + \mathbf{f}^{p}\right), \nonumber \\ & \mathbf{\tau }(s) = -\mathbf{W} \left(\mathbf{W}^T \mathbf{M}_q^{-1} \mathbf{W}\right)^{-1} \mathbf{W}^T \mathbf{M}_q^{-1} \left(\frac{\partial \mathbf{z}}{\partial \mathbf{q}}\right)^T \mathbf{f}^{a}. \end{align}
3. Mobility Space Bounded by Ruled Surfaces
3.1. Polygon approach
The general mobility problem for a robot (machine) following a prescribed path (process) is, for example, the following: evaluate
$\dot{s}(t)$
with
$s(0)=0, s(t_F)=s_F, \dot{s}(0)=0, \dot{s}(t_F)=0$
in such a way that some performance criterion will be met. Such criteria might be minimum time, minimum energy, maximum mobility, and the like. The solution of this problem is practically constrained, where the most important ones are as follows.
First, the driving torques or forces are limited, which means from the relations above
\begin{align} T_{i,\textrm{min}} \leq [A_i(s)& (\dot{s}^2)^{\prime } + B_i(s) (\dot{s}^2) + C_i(s)] \leq T_{i,\textrm{max}}, \nonumber \\[3pt] (\dot{s}^2)^{\prime } =& \frac{-B_i(s) (\dot{s}^2) - C_i(s) + \left (\begin{array}{cc} +T_{i,\textrm{max}}\\ -T_{i,\textrm{min}} \end{array}\right )}{A_i(s)}, \qquad (\dot{s}^2)_{A=0} = \frac{-C_i(s) + \left (\begin{array}{cc} +T_{i,\textrm{max}}\\ -T_{i,\textrm{min}} \end{array}\right )}{B_i(s)}, \end{align}
where the last equation can be seen as a further additional constraint. Other possible constraints are the following: The angular or translational velocities of constraining elements may be limited due to some maximum speeds of the drive train components
$(\dot{q}_{i,\textrm{min}} \leq [q_i^{\prime }\dot{s}] \leq \dot{q}_{i,\textrm{max}})$
, and the path velocity itself might become constrained by some manufacturing process
$(\!-v_{\textrm{max}} \leq |\mathbf{r}^{\prime }|\dot{s} \leq +v_{\textrm{max}})$
with the vector
$\mathbf{r}$
from the constrained machine (robot) element under consideration to a process path point. These relations define together a maximum velocity
$\dot{s}_L$
along the path which must not be exceeded (Fig. 1):
Figure 1. Polygons of possible motion for fixed s (see also ref. [Reference Pfeiffer1]).
\begin{equation} 0 \leq (\dot{s}^2) \leq (\dot{s}^2)_L, \qquad \textrm{with}\qquad (\dot{s}^2)_L = \textrm{min}\left [\left(\frac{\dot{q}_{i,\textrm{max}}}{q_i^{\prime }}\right)^2,\quad \left(\frac{v_{\textrm{max}}}{|\mathbf{r}^{\prime }|}\right)^2,\quad (\dot{s}^2)_{A=0} \right ]. \end{equation}
Additional limits may enter by process forces, usually in the form of process constraints. A typical example is force vector direction, which occurs when a robot follows a polishing trajectory requiring a certain amount of contact pressure with respect to a prescribed direction. Examples of that type are also typical for many machine tools. Evaluating the polygons of mobility space, such conditions additionally constrain the field of allowed motion, see Fig. 2.
Figure 2. Polygon of possible motion for s = constant, additional force limit.
A first step to the solution of the mobility problem may be done in the following way: We look at Eq. (13) for the limiting cases
$(T_{i,\textrm{min}}, T_{i,\textrm{max}})$
stating that maximum mobility can only be achieved by applying in a maximum number of joints the limiting torques or forces. In addition, we may influence mobility by the distribution of drives in the various DOF elements. Operating at the power limits, we get the two equations
\begin{align} (\dot{s}^2)^{\prime }_{T_{\textrm{max}}} = \frac{-B_i(s) (\dot{s}^2) - C_i(s) + T_{i,\textrm{max}}}{A_i(s)}, \qquad (\dot{s}^2)^{\prime }_{T_{\textrm{min}}} = \frac{-B_i(s) (\dot{s}^2) - C_i(s) - T_{i,\textrm{min}}}{A_i(s)}, \end{align}
which define two straight lines in the
$[(\dot{s}^2)^{\prime }, (\dot{s}^2)]$
-plane, Fig. 1.
The altogether
$(2f_D)$
straight lines (
$f_D \leq f$
) form a polygon confined at the left side by the axis
$(\dot{s}^2)=0$
and at the right side by the (
$T_{i,\textrm{min}}, T_{i,\textrm{max}}$
)-straight-lines or by the constraint
$(\dot{s}^2)_L$
given by Eq. (14). Additional limits may enter by the constraint forces and corresponding requirements, Fig. 2. Without violating the constraints, which may be extended without much problems, motion can take place only within the polygons or on their straight line boundaries, which contain the following information: the maximum possible velocity
$\dot{s}_{\textrm{max}}^2$
and for each point
$(\dot{s}^2)$
a maximum and a minimum acceleration or deceleration [
$(\dot{s}^2)^{\prime }_{\textrm{max}}, (\dot{s}^2)^{\prime }_{\textrm{min}}$
]. For example, finding time-optimal solutions we have to go along the assemblage of these polygons and generate what we call extremals. Combining all polygons for all path points s, we obtain a constrained phase space bounded by ruled surfaces due to the straight line characteristics of the polygons. We call this motion or mobility space. These polygons appear as plain cuts perpendicular to the s-axis, see results of Fig. 10.
3.2. Polygon evaluation
Many ways of polygon evaluation are conceivable, where from a test of several methods the numerically most effective one has been selected. In a first step, all double straight lines are assorted according to their width
$d_i \cos \gamma _i, \tan \gamma _i = \frac{B_i}{A_i}$
, see Fig. 3. For evaluating the smallest polygon as formed by the double lines of Eq. (15) we consider an assemblage of vertical straight lines and determine for each individual vertical line m the smallest possible distance of points with positive and negative torques. Start is the strip with largest distance
$d_i \cos \gamma _i$
, blue lines k and points Fig. 3. Looking at the second largest strip (green lines l), there are two possibilities of intersections. The green strip lies completely within the blue one or only one green point alone lies within the blue strip distance. Anyway, we proceed with the combination of smallest distance. This algorithm is continued up to the last pair of points giving the smallest distance for the vertical cut under consideration. Considering very many cuts within the limitations brings us to a collection of solution points forming again straight lines for the final solution area for s = constant.
Figure 3. Polygon evaluation – intersections at some given
$(\dot{s}^2)_m$
[s = constant, plus-sign for
$T_{i,\textrm{max}}$
, minus-sign for
$T_{i,\textrm{min}}$
].
The formal steps are (Fig. 3)
\begin{align} \Delta S_{m(i,j)} &= \textrm{min}_{\begin{subarray}{1} i=1,2\ldots n \\j=1,2\ldots n \end{subarray}} \bigl \lbrace S_{\textrm{max}}[(\dot{s}^2)_m, (\dot{s}^2)^{\prime }_i] - S_{\textrm{min}}[(\dot{s}^2)_m, (\dot{s}^2)^{\prime }_j] \bigr \rbrace, \nonumber \\ &\quad P_{\textrm{total}} = \bigcup _{s=s_0}^{s_n} P_s(s), \qquad P_s(s) = \bigcup _{(\dot{s}^2)=0}^{(\dot{s}^2)=(\dot{s}^2)_{\textrm{max}}} \Delta S_{m(i,j)}, \end{align}
where the
$S_{\textrm{max}, \textrm{min}}$
are depicted by Fig. 3,
$P_s$
stands for the polygon structure composed by the
$\Delta S_m$
, and
$P_{\textrm{total}}$
is the complete structure composed by all
$\Delta S_m$
.
In Fig. 3, all points along the cut m are within the blue strip points, being the largest one. One of the dark blue points lies within the two black points, which together with one dark blue point define the smallest range of allowed motion for the corresponding cut. The smallest distance of two points is then the result for one cut m. These two points usually are not two points of the same robot link, but from different ones. This makes a consistent algorithm difficult. But it is mandatory that the upper point comes from a
$T_{\textrm{max}}$
-line and the lower one from a
$T_{\textrm{min}}$
-line.
3.3. Surface differential geometry
The surface differential geometry is not used directly in the following evaluation, but elements of it are needed, when determining time-optimal solutions. For this case, an integration from one polygon line to the next one will be necessary as depicted in Fig. 5. Differential geometry offers understanding and insight.
The polygons of the preceding Figs. 1–3 are for one specific s. Arranging the polygons for all s along a prescribed path results in a mountain-like structure of ruled surfaces as shown by Figs. 4 and 5, see also the robot example of Fig. 10. Applying to these structural elements classical surface theory [Reference Zeidler, Schwarz and Hackbusch13] gives the fundamental form of these ruled surfaces as generated by the relevant polygon lines. According to the relations (15), we put
$\bar{B} = B(s)/A(s)$
not considering here the case A = 0.
Figure 4. Polygon arrangement and parameter representation.
Figure 5. Polygon arrangement and integration along the ruled surface.
As a first step, we introduce the parameters (u, v), where u follows a selected polygon line from
$\mathbf{r}_0$
to
$\mathbf{r}_1$
, and v = s is the path coordinate. The angle
$\gamma$
is the slope given in the specific coordinate system of Fig. 4. According to Eq. (15) and Fig. 1 the angle
$\gamma$
results from (
$\tan \gamma (s) = \bar{B}(s)$
). Note that the expression
$\bar{B} = \bar{B}(s)$
and from that
$\gamma = \gamma (s) = \gamma (v)$
. Keeping that in mind and using the relations
\begin{equation} E(u,v) = \mathbf{r}_u \cdot \mathbf{r}_u, \quad F(u,v) = \mathbf{r}_u \cdot \mathbf{r}_v, \quad G(u,v) = \mathbf{r}_v \cdot \mathbf{r}_v, \qquad \mathbf{r}_u = \frac{\partial \mathbf{r}}{\partial u}, \quad \mathbf{r}_v = \frac{\partial \mathbf{r}}{\partial v}, \end{equation}
together with vector
$\mathbf{r}$
from Fig. 4 the first fundamental form of the surface writes (
$( )^{\prime } = \frac{\partial }{\partial s}$
)
\begin{equation} E(u,v) = 1, \qquad F(u,v) = 0, \qquad G(u,v) = 1 + (u \gamma ^{\prime })^2, \qquad \gamma ^{\prime } = \frac{d \gamma }{ds} = -\biggl (\frac{\bar{B}^{\prime }}{1 + \bar{B}^2}\biggr ). \end{equation}
In a similar way, we determine the second fundamental form using the well-known relations
\begin{align} L(u,v) =& \mathbf{n}^T \cdot \mathbf{r}_{uu}, \quad M(u,v) = \mathbf{n}^T \cdot \mathbf{r}_{uv}, \quad N(u,v) = \mathbf{n}^T \cdot \mathbf{r}_{vv}, \nonumber \\ \mathbf{r}_{uu} =& \frac{\partial ^2 \mathbf{r}}{\partial u^2}, \quad \mathbf{r}_{uv} = \frac{\partial ^2 \mathbf{r}}{\partial u \partial v}, \quad \mathbf{r}_{vv} = \frac{\partial ^2 \mathbf{r}}{\partial v^2}, \qquad \quad \mathbf{n} = \frac{\mathbf{r}_u \times \mathbf{r}_v}{|\mathbf{r}_u \times \mathbf{r}_v|} = \frac{1}{\sqrt{1 + (u \gamma ^{\prime })^2}} \left ( \begin{array}{c} u \gamma ^{\prime } \\ +\sin \gamma \\ -\cos \gamma \end{array} \right ), \end{align}
which finally gives
\begin{align} L(u,v) = 0, \qquad M(u,v) = 0, \qquad N(u,v) =& - \frac{u \gamma ^{\prime \prime }}{\sqrt{1 + (u \gamma ^{\prime })^2}}, \nonumber \\[3pt] \gamma ^{\prime \prime } =& \frac{d^2 \gamma }{ds^2} = -\frac{(1 + \bar{B}^2) \bar{B}^{\prime \prime } - 2\bar{B}(\bar{B}^{\prime })^2}{(1+\bar{B}^2)^2} \end{align}
Knowing the first and second fundamental form, Gauss and mean curvatures can be determined by the expressions
\begin{equation} K = \frac{L N - M^2}{E G - F^2} = 0, \qquad \quad H = \frac{LG-2FM+EN}{2(EG-F^2)} = \frac{N}{2 G} \end{equation}
by considering the results above. The main curvatures
$k_i$
follow from the equation
$(k_i^2 - 2Hk_i + K = 0)$
. With K = 0, we get
\begin{equation} k_1 = K = 0 \quad (\textrm{u-direction}), \qquad k_2 = 2H = - \frac{u \gamma ^{\prime \prime }}{(1 + (u \gamma ^{\prime })^2)^{3/2}} \quad (\textrm{v=s-direction}). \end{equation}
The Gauss curvature is zero, K = 0, a condition defining ruled surfaces. The mean curvature H exists only in path direction s = v and depends on path geometry and certain mass effects.
Figure 5 can be used to organize an integration following the ruled surface of the mobility space. This will be necessary for example evaluating the extremals, which go along the ruled surfaces stepping from some polygon i to the neighboring polygon (i + 1) (see chapter 5.2). The problem is solved by considering the following equations:
\begin{align} & \mathbf{A}(s_i) (\dot{s}^2)_i^{\prime } + \mathbf{B}(s_i) (\dot{s}^2)_i + \mathbf{C}(s_i) = \mathbf{T}(s_i), \nonumber \\[3pt] & \mathbf{A}(s_{i+1}) (\dot{s}^2)_{i+1}^{\prime } + \mathbf{B}(s_{i+1}) (\dot{s}^2)_{i+1} + \mathbf{C}(s_{i+1}) = \mathbf{T}(s_{i+1}), \nonumber \\[3pt] & s_{i+1} = s_i + \Delta s, \qquad (\dot{s}^2)_{i+1} = (\dot{s}^2)_i + \Delta (\dot{s}^2), \qquad (\dot{s}^2)^{\prime }_{i+1} = (\dot{s}^2)^{\prime }_i + \Delta (\dot{s}^2)^{\prime }, \nonumber \\[3pt] &\mathbf{D}_{i+1} = \mathbf{D}_{i} + \mathbf{D}^{\prime } \Delta s, \qquad \quad \mathbf{D} = \mathbf{A},\mathbf{B},\mathbf{C},\mathbf{T} \end{align}
Knowing
$\Delta s$
these relations is enough to determine the unknown quantities for the polynom (i + 1) by an iteration process being necessary for two reasons: first to realize numerical stability and second to meet the correct line of polynom (i + 1) also in the case of an integration step passing an intersection of two polygon lines.
4. Example Multi-DOF-Robot with Revolute Joints
In the following, we shall consider the magnitudes used in Eqs. (11) and (12), which stand for the equations of motion and those for the constraint forces. Inertial reference is applied.
4.1. Kinematics
A robot with
$n_q$
revolute joints can be described by Cartesian
$\mathbf{z}$
-coordinates and by angular
$\mathbf{q}$
-coordinates. The projections (
$\mathbf{z} \rightarrow \mathbf{q} \rightarrow s$
) have been discussed before. With respect to the
$\mathbf{q}$
-coordinates, relative and absolute versions are needed (Fig. 6)
Figure 6. Geometry of a multi-DOF robot.
\begin{equation} \bar{q}_i = \frac{\Pi }{2} - \sum _{j=1}^i q_j = \bar{q}_{i-1} - q_i, \qquad q_i = \bar{q}_{i-1} - \bar{q}_{i}, \qquad \bar{q}_{0} = \frac{\Pi }{2}. \end{equation}
The
$\mathbf{z}$
-coordinates are defined in the following way (2):
\begin{align} &{\dot{\mathbf{z}}} = ({\dot{\mathbf{z}}_{1}}{\dot{\mathbf{z}}_{2}} \ldots \ldots \ldots \ldots{\dot{\mathbf{z}}_{n}})^T, \qquad \quad \bar{\mathbf{q}} = (q_0 \bar{q}_1 \bar{q}_2 \ldots \ldots \ldots \bar{q}_{n_q}^T), \nonumber \\ &{\dot{\mathbf{z}}_{i}} = \left (\begin{array}{cc} \dot{\mathbf{r}}_i \\ \\[-8pt] \mathbf{\omega }_i \end{array}\right ), \quad{\ddot{\mathbf{z}}_{i}} = \left (\begin{array}{cc} \ddot{\mathbf{r}}_i \\ \\[-8pt] \dot{\mathbf{\omega }}_i \end{array}\right ), \quad \dot{\mathbf{r}}_i = \left (\begin{array}{ccc} \dot{x} \\ \\[-8pt] \dot{y} \\ \\[-8pt] \dot{z} \end{array}\right )_i, \quad \dot{\mathbf{\omega }}_i = \left (\begin{array}{ccc} \dot{\omega }_x \\ \\[-8pt] \dot{\omega }_y \\ \\[-8pt] \dot{\omega }_z \end{array}\right )_i, \nonumber \\ & \mathbf{z} \in \Re ^{n}, \bar{\mathbf{q}} \in \Re ^{n_q} \mathbf{z}_i \in \Re ^6, \mathbf{r}_i \in \Re ^3, \mathbf{\omega }_i \in \Re ^{3}. \end{align}
With these definitions, the joint vectors
$\mathbf{z}_{Ji}$
and the center of mass vectors
$\mathbf{z}_{Ci}$
possess the following elements (J = joint point, C = center of mass):
\begin{align} \mathbf{r}_{Ji} = \sum _{j=1}^{i-1} l_j \left (\begin{array}{ccc} \cos \bar{q}_j \cos \bar{q}_0 \\ \\[-8pt] \cos \bar{q}_j \sin q_0 \\ \\[-8pt] \sin \bar{q}_j \end{array}\right ), \quad \mathbf{r}_{Ci} = \sum _{j=1}^{i-1} l_j \left (\begin{array}{ccc} \cos \bar{q}_j \cos q_0 \\ \\[-8pt] \cos \bar{q}_j \sin q_0 \\ \\[-8pt] \sin \bar{q}_j \end{array}\right ) + d_i \left (\begin{array}{ccc} \cos \bar{q}_i \cos q_0 \\ \\[-8pt] \cos \bar{q}_i \sin q_0 \\ \\[-8pt] \sin \bar{q}_i \end{array}\right ) \end{align}
It should be noted that for the rotation around the vertical inertial
$z_1$
-axis (Fig. 6) the above vectors are zero,
$\mathbf{r}_{Ji} = 0, \mathbf{r}_{Ci} = 0$
. The angular velocities
$\mathbf{\omega }_i$
are determined by the well-known relations
${}_{I}{\tilde{\mathbf{\omega }}}_i = \dot{\mathbf{A}}_{IB} \mathbf{A}_{BI} = \dot{\mathbf{A}}_{IB} \mathbf{A}_{IB}^T$
with the result [Reference Pfeiffer2] (I = inertial, B = body)
\begin{align} &{}_{I}{\mathbf{\omega }}_i = \left (\begin{array}{ccc} -\dot{\bar{q}}_i \sin q_0 \\ \\[-8pt] +\dot{\bar{q}}_i \cos q_0 \\ \\[-8pt] \dot{q}_0 \end{array} \right ), \quad{}_{B}{\mathbf{\omega }}_i = \left (\begin{array}{ccc} -\dot{q}_0 \sin \bar{q}_i \\ \\[-8pt] \dot{\bar{q}}_i \\ \\[-8pt] +\dot{q}_0 \cos \bar{q}_i\end{array} \right ), \quad \mathbf{A}_{IB} = \left(\begin{array}{c@{\quad}c@{\quad}c} \cos q_0 cos \bar{q}_i & -\sin q_0 & \cos q_0 \sin \bar{q}_i \\ \\[-8pt] \sin q_0 cos \bar{q}_i & +\cos q_0 & \sin q_0 \sin \bar{q}_i \\ \\[-8pt] -\sin \bar{q}_i & 0 & \cos \bar{q}_i \end{array}\right) \end{align}
The matrix
$\mathbf{A}_{IB}$
follows from two rotations, first around the inertial z-axis, and second around the body-fixed y-axis. For i = 1 (first DOF with
$q_0$
), the angular velocity is
${}_{I}{\mathbf{\omega }}_1 ={}_{B}{\mathbf{\omega }}_1 = ( 0 0 \dot{q}_0)^T$
. Establishing the equations of motion, the derivations (
$(\frac{\partial \mathbf{z}}{\partial \bar{\mathbf{q}}}), \bar{\mathbf{q}}^{\prime }, \bar{\mathbf{q}}^{\prime \prime }$
) are needed. They can be evaluated from the relations (26) and (27). In the following, only a few examples are given.
The gradient
$(\frac{\partial \mathbf{z}}{\partial \bar{\mathbf{q}}})$
follows from (example
${}_{I}{\dot{\mathbf{z}}}_{Ji}$
)
\begin{align} &{}_{I}{\dot{\mathbf{z}}}_{Ji} = \left(\frac{\partial \mathbf{z}}{\partial \bar{\mathbf{q}}}\right) \dot{\bar{\mathbf{q}}} = \left (\begin{array}{cccccc} \sum _{j=1}^{i-1} l_j [\! -\cos q_0 \sin \bar{q}_j \dot{\bar{q}}_j - \sin q_0 \cos \bar{q}_j \dot{q}_0 ] \\ \\[-9pt] \sum _{j=1}^{i-1} l_j [ \!-\sin q_0 \sin \bar{q}_j \dot{\bar{q}}_j + \cos q_0 \cos \bar{q}_j \dot{q}_0 ] \\ \\[-9pt] \sum _{j=1}^{i-1} l_j [ + \cos \bar{q}_j \dot{\bar{q}}_j ] \\ \\[-9pt] -\dot{\bar{q}}_i \sin q_0 \\ \\[-9pt] +\dot{\bar{q}}_i \cos q_0 \\ \\[-9pt] \dot{q}_0 \end{array}\right ). \end{align}
Knowing
$(\frac{\partial \mathbf{z}}{\partial \bar{\mathbf{q}}})$
, we get by an additional derivation the matrix for
$(\frac{\partial ^2 \mathbf{z}}{\partial \bar{\mathbf{q}}^2})$
. The projections of
$\bar{\mathbf{q}}$
with respect to s are evaluated numerically by
\begin{equation} \bar{\mathbf{q}}^{\prime } = \frac{\bar{\mathbf{q}}(s_{i+1}) - \bar{\mathbf{q}}(s_{i-1})}{s_{i+1} - s_{i-1}}, \qquad \quad \bar{\mathbf{q}}^{\prime \prime } = \frac{\bar{\mathbf{q}}(s_{i+1}) - 2 \bar{\mathbf{q}}(s_i) + \bar{\mathbf{q}}(s_{i-1})}{[\frac{1}{2}(s_{i+1} - s_{i-1})]^2}. \end{equation}
To determine the same information for the angle
$q_0$
, we start with the (x,y,z)-position of each trajectory point and calculate
$q_0$
and its derivatives (Fig. 6)
\begin{align} \tan q_0 = \left(\frac{y}{x}\right)_{\textrm{trajectory}}, \quad q_0^{\prime } =& \frac{y^{\prime } x - y x^{\prime }}{x^2 + y^2}, \nonumber \\[3pt] q_0^{\prime \prime } =& \biggl [\frac{y^{\prime \prime } x - y x^{\prime \prime }}{x^2 + y^2} + 2 \frac{x^{\prime } y^{\prime } (y^2 - x^2) - xy((y^{\prime })^2-(x^{\prime })^2)}{(x^2 + y^2)^2}\biggr ] \end{align}
For our specific case of a n-link robot following a trajectory, we determine
$\bar{\mathbf{q}} = \bar{\mathbf{q}}(\mathbf{r}(s))$
by an optimization algorithm.
For positioning the robot end effector at the target point, we apply formula (26) and require (Fig. 6)
\begin{align} \mathbf{r}_{Jn} = \mathbf{r}(\bar{\mathbf{q}}(s)) = \sum _{j=1}^{n} l_j \left (\begin{array}{ccc} \cos \bar{q}_j \cos q_0 \\ \\[-9pt] \cos \bar{q}_j \sin q_0 \\ \\[-9pt] \sin \bar{q}_j \end{array}\right ) = \left (\begin{array}{ccc} x \\ \\[-9pt] y \\ \\[-9pt] z \end{array}\right )_{\textrm{trajectory}}, \end{align}
where the path data
$(x y z)^T_{\textrm{trajectory}}$
are given. The relation above represents then a nonlinear set of equations for the determination of robot coordinates
$\bar{\mathbf{q}}$
, being solved by standard methods [Reference Zeidler, Schwarz and Hackbusch13].
4.2. Constraint geometry
A two-link robot tracking a path moves with six constraints, three constraints for vertical and two horizontal joints and three constraints for keeping the robot end effector on a given trajectory, Fig. 8. Starting with the three robot constraints, regarding the structure of Fig. 8 indicating a circular motion of all links, the joint constraints write
\begin{align} &\Phi _0 = x_1^2 + y_1^2 - (l_1 \cos \bar{q}_1)^2 = 0, \nonumber \\[3pt] & \Phi _1 = x_1^2 + y_1^2 + z_1^2 - d_1^2 = 0, \qquad \Phi _2 = (x_2-x_{l1})^2 + (y_2-y_{l2})^2 + (z_2-z_{l1})^2 - d_2^2 = 0, \end{align}
where
$(x_{l2}, y_{l2}, z_{l2}) = \frac{l_1}{d_1} (x_1,y_1,z_1)$
are the coordinates of the end point of link 1. Following some trajectory produces three additional constraints
\begin{equation} \Phi _{3,4,5} = [(x) (y) (z) ]^T - [(x_0+\xi ) (\eta ) (\!-h) ]_{\textrm{trajectory}}^T = \mathbf{0}. \end{equation}
These equations must be differentiated twice for the corresponding form [
$\dot{\mathbf{\Phi }} = \mathbf{W}^T \dot{\mathbf{z}} + \bar{\mathbf{w}} = \mathbf{0},\ \ddot{\mathbf{\Phi }} = \mathbf{W}^T \ddot{\mathbf{z}} + \hat{\mathbf{w}} = \mathbf{0}$
] of Eq. (5), which results in
\begin{align} \mathbf{W}^T =& \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} x_1 & y_1 & 0 & 0 & 0 & 0 \\ \\[-8pt] x_1 & y_1 & z_1 & 0 & 0 & 0 \\ \\[-8pt] -\frac{l_1}{d_1} \Delta x & -\frac{l_1}{d_1} \Delta y & -\frac{l_1}{d_1} \Delta z & \Delta x & \Delta y & \Delta x \\ \\[-8pt] & & \mathbf{W}_0 & & & \\ \\[-8pt] 0 & 0 & 0 & 1 & 0 & 0 \\ \\[-8pt] 0 & 0 & 0 & 0 & 1 & 0 \\ \\[-8pt] 0 & 0 & 0 & 0 & 0 & 1 \\ \\[-8pt] & & \mathbf{W}_0 & & & \end{array}\right), \quad \qquad \mathbf{z} = \left (\begin{array}{cccccccc} x_1 \\ \\[-8pt] y_1 \\ \\[-8pt] z_1 \\ \\[-8pt] \mathbf{w}_0 \\ \\[-8pt] x_2 \\ \\[-8pt] y_2 \\ \\[-8pt] z_2 \\ \\[-8pt] \mathbf{w}_0 \end{array}\right ), \nonumber \\ \bar{\mathbf{w}} =& \left (\begin{array}{cccccccc} \frac{1}{2} (l_1^2 \sin 2\bar{q}_1) \dot{\bar{q}}_1 \\ \\[-8pt] 0 \\ \\[-8pt] 0 \\ \\[-8pt] \mathbf{w}_0 \\ \\[-8pt] -\dot{\xi } \\ \\[-8pt] -\dot{\eta } \\ \\[-8pt] 0 \\ \\[-8pt] \mathbf{w}_0 \end{array}\right ), \quad \qquad \hat{\mathbf{w}} = \left (\begin{array}{cccccccc} \dot{x}_1^2 + \dot{y}_1^2 + l_1^2 [\frac{1}{2} (\sin 2\bar{q}_1) \ddot{\bar{q}}_1 + (\!\cos 2\bar{q}_1 ) \dot{\bar{q}}_1^2] \\ \\[-8pt] \dot{x}_1^2 + \dot{y}_1^2 + \dot{z}_1^2 \\ \\[-8pt] \Delta \dot{x}_1^2 + \Delta \dot{y}_1^2 + \Delta \dot{z}_1^2 \\ \\[-8pt] \mathbf{w}_0 \\ \\[-8pt] -\ddot{\xi } \\ \\[-8pt] -\ddot{\eta } \\ \\[-8pt] 0 \\ \\[-8pt] \mathbf{w}_0 \end{array}\right ), \end{align}
with
$\Delta x = x_2 - \frac{l_1}{d_1} x_1$
, etc. To meet the formal requirements of Eqs. (5) and (25) null-matrix,
$\mathbf{W}_0$
has the dimension
$\Re ^{3,6}$
and null-vector
$\mathbf{w}_0$
the dimension
$\Re ^{3}$
. The constraints do not include rotations. For constraint kinematics, we have to determine the robot coordinates for some given path point. This is done by going from robot workspace to joint space. The resulting magnitudes are used to evaluate the derivatives with respect to the path coordinate s by numerical methods. The constraint matrix
$\mathbf{W}$
is needed mainly for determining the constraint forces. At the end of the section, we consider an example.
The motion of the robot may start at a point
$(\xi _0,\eta _0)$
and end at
$(\xi _E,\eta _E)$
. For generating a spiral path, the number is
$n_x$
, so the repeating circle step is
$\Delta \xi = (\xi _E - \xi _0)/n_x$
. A point on the “moving” circle is
$(\xi _C = r \cos \varphi, \eta _C = r \sin \varphi )$
with r the circle radius. With these data, the end effector position and the rate of change with the path coordinate s are determined as
\begin{align} \xi =& \xi _0 + n \Delta \xi + \left(\frac{\Delta \xi }{2 \Pi }\right) \varphi + r \cos \varphi, \qquad \quad \eta = \eta _0 + r \cos \varphi, \nonumber \\[3pt] \frac{\partial s}{\partial \varphi } =& \sqrt{\left(\frac{\partial \xi }{\partial \varphi }\right)^2 + \left(\frac{\partial \eta }{\partial \varphi }\right)^2 } = \sqrt{\left(\frac{\Delta \xi }{2 \Pi }\right)^2 - 2 \left(\frac{\Delta \xi }{2 \Pi }\right) r \sin \varphi + r^2}, \qquad \quad ( )^{\prime } = \left(\frac{\partial }{\partial s}\right). \end{align}
The number n is the number of circles already performed,
$n \leq n_x$
. Necessary derivatives write
\begin{align} \xi ^{\prime } =& \left[\left(\frac{\Delta \xi }{2 \Pi }\right) - r \sin \varphi \right] \varphi ^{\prime }, \qquad \xi ^{\prime \prime } = \left[\left(\frac{\Delta \xi }{2 \Pi }\right) - r \sin \varphi \right]\left(\frac{\partial \varphi ^{\prime }}{\partial \varphi }\right)\varphi ^{\prime } - (r \cos \varphi ) (\varphi ^{\prime })^2 \nonumber \\[3pt] \eta ^{\prime } =& (r \cos \varphi ) \varphi ^{\prime }, \qquad \eta ^{\prime \prime } = (r \cos \varphi )\left(\frac{\partial \varphi ^{\prime }}{\partial \varphi }\right)\varphi ^{\prime } - (r \sin \varphi ) (\varphi ^{\prime })^2 \nonumber \\ &\left(\frac{\partial \varphi ^{\prime }}{\partial \varphi }\right)\varphi ^{\prime } = \frac{\left(\frac{\Delta \xi }{2 \Pi }\right)\left(r \cos \varphi \right)}{\left(\frac{\Delta \xi }{2 \Pi }\right)^2 - 2 \left(\frac{\Delta \xi }{2 \Pi }\right) r \sin \varphi + r^2} \end{align}
Finally, we present an example with the equations of motion fulfilling all constraints with exception of the ground contact. The requirement for the end effector to be on a height
$z_T = \textrm{constant}$
gives
\begin{align} & \mathbf{\Phi } = z[\bar{\mathbf{q}}(s)] - z_T = 0, \nonumber \\ & \dot{\mathbf{\Phi }} = \left(\frac{\partial z}{\partial \bar{\mathbf{q}}}\right) \dot{\bar{\mathbf{q}}} = \mathbf{W}_{ps}^T \dot{\bar{\mathbf{q}}} = 0, \nonumber \\ & \ddot{\mathbf{\Phi }} = \mathbf{W}_{ps}^T \ddot{\bar{\mathbf{q}}} + \left(\frac{d\mathbf{W_{ps}}^T}{dt}\right) \dot{\bar{\mathbf{q}}} = \mathbf{W}_{ps}^T \ddot{\bar{\mathbf{q}}} + \hat{w}_{ps} = 0, \nonumber \\ & \mathbf{W}_{ps}^T = \left(\frac{\partial z}{\partial \bar{\mathbf{q}}}\right) = (0 l_1 \textrm{cos} \bar{q}_1 l_2 \textrm{cos} \bar{q}_2), \qquad \hat{w}_{ps} = \left(\frac{d\mathbf{W_{ps}}^T}{dt}\right) \dot{\bar{\mathbf{q}}} \nonumber \\ & z = \sum _{j=1}^{n_q} l_j \textrm{sin}(\bar{q}_j), \qquad \hat{w}_{ps} = - \sum _{j=1}^{n_q} (l_j \textrm{sin} \bar{q}_j) (\bar{q}_j^{\prime })^2 (\dot{s}^2). \end{align}
The expression for z follows from Eq. (31), the resulting constraint forces (torques) from the relations (12).
4.3. Masses and forces
According to Eq. (1) the mass matrix and its derivatives write
\begin{align} & \mathbf{M}_i = \begin{pmatrix} m\mathbf{E} & m \tilde{\mathbf{r}}_{O'S}^{T} \\ \\[-8pt] m \tilde{\mathbf{r}}_{O'S} & \mathbf{\Theta }_{O'} \end{pmatrix}_i\ \in \Re ^{n_m,n_m}, \quad \textrm{with}\quad \mathbf{\Theta }_{O'i} = -\sum _{\Delta m} [\tilde{\mathbf{r}}_{O'S} \tilde{\mathbf{r}}_{O'S} \Delta m]_i \nonumber \\ \frac{d\mathbf{M}_i}{dt} = & \begin{pmatrix} \mathbf{0} & m \dot{\tilde{\mathbf{r}}}_{O'S}^{T} \\ \\[-8pt] m \dot{\tilde{\mathbf{r}}}_{O'S} & \dot{\mathbf{\Theta }}_{O'} \end{pmatrix}_i, \quad \frac{d\mathbf{\Theta }_{O'i}}{dt} = -\sum _{\Delta m} [\dot{\tilde{\mathbf{r}}}_{O'S} \tilde{\mathbf{r}}_{O'S} + \tilde{\mathbf{r}}_{O'S} \dot{\tilde{\mathbf{r}}}_{O'S}]_i \Delta m_i \end{align}
For some link i, we choose as a reference point the center of mass S, which makes
$\mathbf{r}_{O'S} = 0$
and
$\dot{\mathbf{r}}_{O'S} = 0$
. A special case is the first coordinate
$q_0$
, where the reference point
$O^{\prime }$
is the coordinate origin and the distance to the link centers of mass
$(\mathbf{r}_{O'S})_i \ne 0$
. For this case and according to Eq. (26), we have
$(\mathbf{r}_{O'S})_i = \mathbf{r}_{Ci}$
. The moment of inertia for the bar-like links alone is
$\mathbf{\Theta }_{Si} = \frac{1}{3} m_i l_i^2 [1 - 3(\frac{d}{l}) + 3(\frac{d}{l})^2]$
.
Figure 7. Trajectory, torques and forces at link i.
Figure 8. Constraints – geometry and torques.
As a further step, we have to evaluate the forces and torques considered in an inertial system. The external and applied forces and torques (Fig. 7) are
\begin{align}{}_{I}{\mathbf{f}}^{e}_i =& [ 0 0 (\!-m_i g) 0 0 0 ]^T, \quad{}_{I}{\mathbf{f}}^{e}_0 = \mathbf{0}, \qquad{}_{I}{\mathbf{f}}^{a}_0 = [ 0 0 0 0 0 (T_0) ]^T, \nonumber \\[3pt] {}_{I}{\mathbf{f}}^{a}_{i\gt 0} =& [ 0 0 0 (\!-(T_{a(i+1)} - T_{ai}) \sin q_0) (+(T_{a(i+1)} - T_{ai}) \cos q_0) 0 ]^T, \end{align}
5. Results for a Robot with Three Revolute Joints
An illustrative example is a two-link robot performing a circular vertical path, for which we present some comparisons with old measurements of the time-optimal path torques, Fig. 9 (top, left). Theory and measurements compare well, the high frequency oscillations of the measured data are due to the robot measurement system [Reference Pfeiffer2, Reference Johanni3, Reference Pfeiffer14]. The results confirm the basic idea of the paper.
Figure 9. Comparison theory/measurements for a two-link robot [Reference Pfeiffer2, Reference Johanni3].
5.1. Tracking a given trajectory
To illustrate more in detail the theory above, we consider the motion along a horizontal circle. Evaluating Eq. (15) for each trajectory point with the coordinate s results in Fig. 10, which depicts on the left side (top) the horizontal circle with a robot indication and in addition polygons for six trajectory points. These polygons are scaled equally, giving some feeling for the motion capabilities of the robot around the circle. The points farthest away from the robot base show relatively small motion areas due to the fact that the robot, being there in a stretched position, has to counterbalance his own weight, and very large moments of inertia for the vertical drive leave less power for velocity and acceleration.
At the position of start level and of the position
$180^{\circ }$
, opposite velocities are largest but accelerations diminished. Motion at these points is dominantly performed by the arm drives and not so much by the vertical drive with angular velocity
$\dot{q}_0$
. Another situation is illustrated by the two points nearest to the robot base, exhibiting large acceleration capabilities and medium-sized velocities. They are dominated by the drive around z with
$\dot{q}_0$
.
Beginning at the start position and then going along the trajectory and arranging the six polygons in the [
$(\dot{s}^2)^{\prime }, (\dot{s}^2)$
] - plane comes out with the right picture (top) of Fig. 10, where each element represents a polygon for s = constant. Taking into consideration, some more polygons result in the left picture (bottom) of Fig. 10. As could be expected, we get for the complete trajectory a “line-free” area of motion allowing any solution within the given drive limits
$(T_{i,\textrm{max}}, T_{i,\textrm{min}})$
without touching some constraint. Printing these polygons not onto one plane but extending them along the path coordinate s gives the right graph of Fig. 10 bottom. The “entrance” to this structure corresponds to the polygon at the start point of Fig. 10 (top).
Altogether it is a mountain-like construct generated by straight lines forming ruled surfaces as an exterior boundary. Motion can only take place on these ruled surfaces originating from the extremum drive torques or forces, or it can take place in the space bounded by these ruled surfaces. For ruled surfaces, see ref. [Reference Hoschek15] or elsewhere.
The motion space of Fig. 10 represents a convenient tool for studying various solution and motion concepts. For example, to go with constant velocity within the free space we put
$(\dot{s}^2)^{\prime } = 0$
and get immediately the necessary torques from Eq. (15), namely
$\mathbf{T}(s) = \mathbf{B}(s) (\dot{s}^2) + \mathbf{C}(s)$
. A more interesting case is that of time-minimum motion requiring to find trajectories on the ruled surfaces.
5.2. Extremals
From Eq. (15), the extremals are constructed from the upper part and from the lower part of the polygons, from the side with maximum accelerations
$(\dot{s}^2)^{\prime }_{\textrm{max}}$
containing the max-extremals, and the side with minimum accelerations
$(\dot{s}^2)^{\prime }_{\textrm{min}}$
containing the min-extremals (Fig. 1 and section 3.1). Figure 11 illustrates the projections of these extremals together with the maximum velocities from motion space onto the [
$\dot{s}^2 - s$
] - plane.
Figure 10. Motion areas (polygons) along a horizontal circular trajectory (top) and generation of motion space (bottom).
A time-optimal solution, for example, must be composed by several of these extremals for the following reasons. Requiring
$\dot{s}^2 = 0$
at s = 0 and
$s = s_F$
requires to follow a certain combination of extremals for arriving at the final point. Such a procedure needs an integration of the equations of motion along the ruled surfaces and thus from polygon at s to the next one at (
$s + \Delta s$
). Integration on polygons excludes normally a progress along the rim of the motion space, exceptions are possible [Reference Johanni3].
Figure 11 illustrates that procedure. The blue extremal at the beginning connects s = 0 with the maximum velocity curve at
$s \approx 1.7$
, and the green extremal at the end connects
$s=s_F \approx 8.8$
with
$s \approx 6.9$
. Note that the blue extremals are on the motion space side with maximum accelerations and the green on the side with minimum accelerations. At a possible intersection point of the blue and green extremals, the torques and forces make a corresponding jump, because such intersection points are usually not minimum points with
$A_i=0$
. As a further step, we construct all extremals originating from the saddle points (minimum points) at
$s \approx 2.2$
and at
$s \approx 6.7$
. These are points, where at least one coefficient
$A_i \in \mathbf{A}$
of Eq. (11) vanishes, thus allowing a smooth step from one side of the motion space to the other one. The extremals emanating from these points intersect the extremals coming from the beginning and from the end, and in addition for our example, they themselves intersect at a point s
$\approx$
4.3. The resulting ensemble of six curve elements forms the time-optimal solution for the motion under consideration, avoiding any limits and problems with rim contacts.
5.3. Driving torques
For considering driving torques along a time-optimal solution, we select a trajectory example as it might be used for polishing work. Figure 12 depicts the situation for a spiral trajectory as shown by the left graph. The ruled surface mountain structure is not shown, but only the projection of this construct onto the
$(\dot{s}^2)^{\prime }-\dot{s}^2$
-plane, comparable to Fig. 10. This collection of quite a number of constraining polygons reveals again the useful property of such problems, namely a free area not cut by polygon lines. Within the mountain structure of the mobility space, this area indicates a kind of tunnel, in which any motion might take place without touching limiting constraints.
Figure 11. Field of extremals (blue lines max-extremal, green lines min-extremals) and an extremal selection forming the time-optimal solution.
Figure 12.
Left: trajectory for polishing (robot position as in Fig. 10), middle: collection of polygons, right: joint torques for a two-link robot, black solid
$T_1$
, black dashed
$T_2$
, black dash-dotted
$T_3$
, red line
$(\dot{s}^2)_{\textrm{max}}$
, blue-green lines time-optimal solution (right graph: velocities only qualitative).
Knowing all kinematic data for time-optimal tracking a given path (Fig. 11), it is easy to calculate the necessary torques for following that path just by applying the equations of motion (11) in a reverse way: prescribed kinematics, solve for the torques. The result is given by the right graph of Fig. 12. It demonstrates the necessity that for time-optimal motion at least one of the three drives must work at its limits. For some rough orientation, the time-optimal extremals are indicated. The following conclusions may be drawn: at the beginning and at the end of the path motion is controlled by the maximum torque of the third joint, the two other joints look for balancing. About the path middle, the basic joint around the vertical axis contributes with maximum torque. These activities bring the robot from the start with path velocity zero to the end again with zero velocity.
Figure 13 illustrates the same situation for a trajectory composed of six spiral elements. It is also a numerical test demonstrating numerical stability, which cannot be taken for granted. The structure as shown in Fig. 12 is repeated six times, the properties for each revolution remain approximately the same.
Figure 13.
Left: trajectory for polishing (robot position as in Fig. 10), middle: collection of polygons, right: joint torques for a two-link robot, black solid
$T_1$
, black dashed
$T_2$
, black dash-dotted
$T_3$
, red line
$(\dot{s}^2)_{\textrm{max}}$
, blue-green lines time-optimal solution (right graph: velocities only qualitative).
5.4. Constraint torques
The constraint forces and torques are evaluated according to Section 2. For our specific example, it is assumed that all constraints are already satisfied with the exception of the ground contact, see end of section 4.2. We remember also that constraint forces depend only on path velocity and path coordinate and not on the path acceleration,
$\mathbf{f}^c = \mathbf{f}^c (s, \dot{s}^2)$
, Eq. (12). We shall consider a spiral form path with the properties and results as depicted in Fig. 14, which shows velocities and torques for the time-optimal case.
Figure 14. Trajectory form and results for forces and velocities (right graph: velocities only qualitative).
As an example, this time-optimal velocity distribution and its optimal velocities are taken for evaluating the constraint torques. Figure 14 depicts on the left side the maximum and the optimal velocities and on the right side the corresponding torques necessary to generate these velocities. They are the constraint torques for keeping the robot end effector in a plane with constant z. Roughly spoken, these constraint torques are about 40
$\%$
of the driving torques for the same case, Figs. 12 and 14. Note that these torques are a maximum only for one joint, which is typical for such problems. From the practical standpoint of view, no machine can be operated with all drives working on a maximum power level.
6. Conclusion
The method presented in this paper is formulated generally by considering multibody systems in a first step, and it is then specialized to a robot with revolute joints as an example. Starting with a formulation according to Lagrange I (Jacobi), the DOFs of any multibody system are projected to one prescribed trajectory of arbitrary shape resulting in relations following one DOF only. The projecting tools are constraint derivatives, which are evaluated from the geometry of the multibody structure together with the given trajectory.
The emerging relations represent a system of ordinary linear differential equations in
$(\dot{s})^2$
, the square of path velocity, with highly nonlinear coefficients including the complete MBS (robot) – configuration. They possess a quadratic form related to geodesic type equations. All structural data are compressed in two coefficient systems, an amazing fact. For example, the coefficients A, B, C include the total geometric and topological information of the robot under consideration. And they can be used to build a mobility space, where the motion takes place. This space represents a useful tool for improving and for facilitating design of mechanical systems in general and of robotic systems in particular.
Constructing a mobility space requires some new algorithm. The property “system of ordinary linear differential equations in
$(\dot{s})^2$
” together with the definition of two driving torques
$T_{i,\textrm{min}}, T_{i,\textrm{max}}$
allows to generate two parallel straight lines for every drive component and for constant s, namely in the plane
$[(\dot{s}^2)^{\prime }(s), \dot{s}^2 (s)]$
of modified acceleration and velocity. The intersections of all these lines form a polygon, where motion can take place without constraints. Arranging all polygons along the path coordinate s produces a space bounded by ruled surfaces, called mobility space.
The relations are specified for a robot with any number of revolute joints and numerically evaluated for one with three joints and two links. The results demonstrate a bounded motion space being used for determining time-optimal solutions or for checking over any other motion possibility without violating constraints. They form the bounds of the motion space composed by ruled surfaces. Method is useful for layout purposes.
Author contributions
Not applicable. Contributions are referenced.
Financial support
This research received no specific grant from any funding agency, commercial, or not-for-profit sectors.
Conflicts of interest
The author declares no conflicts of interest exist.
Ethical approval
Not applicable.
Open access
