Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zuo, Guoyu
Li, Mi
Yu, Jianjun
Wu, Chun
and
Huang, Gao
2022.
An Efficient Motion Planning Method with a Lazy Demonstration Graph for Repetitive Pick-and-Place.
Biomimetics,
Vol. 7,
Issue. 4,
p.
210.
Zhang, Yi
Hu, Yunchuan
Lu, Jiakai
and
Shi, Zhiqiang
2022.
Research on Path Planning of Mobile Robot Based on Improved Theta* Algorithm.
Algorithms,
Vol. 15,
Issue. 12,
p.
477.
Li, Jian
Liu, Huan
Sun, Shengbo
Li, Yanqiu
and
Tong, Weihua
2023.
Prediction of Complex Acute Appendicitis Based on HGS-MSVM.
IEEE Access,
Vol. 11,
Issue. ,
p.
84336.
Wu, Chenhao
Fu, Xueliang
Li, Honghui
Hu, Hua
Li, Xue
and
Zhang, Liqian
2023.
A Method Based on Improved Ant Colony Algorithm Feature Selection Combined With GA-SVR Model for Predicting Chlorophyll-a Concentration in Ulansuhai Lake.
IEEE Access,
Vol. 11,
Issue. ,
p.
93180.
Wu, Shuai
Li, Qingxia
and
Wei, Wenhong
2023.
Application of Ant Colony Optimization Algorithm Based on Triangle Inequality Principle and Partition Method Strategy in Robot Path Planning.
Axioms,
Vol. 12,
Issue. 6,
p.
525.
Xu, Yujie
Dai, Chenglin
Han, Shuyi
and
Fu, Mingyu
2023.
Path Planning of Mobile Robot Based on Deep Reinforcement Learning and Improved Artificial Potential Field.
p.
390.
Zhang, Zhihao
Liu, Xiaodong
and
Feng, Boyu
2023.
Research on obstacle avoidance path planning of UAV in complex environments based on improved Bézier curve.
Scientific Reports,
Vol. 13,
Issue. 1,
He, Xiaolin
and
Wang, Yan
2024.
Research and Implementation of Logistics Distribution System Based on Ant Colony Algorithm.
p.
1.
Wang, Shengzhe
Xu, Ziyan
Wang, Yidan
Tan, Ziyao
and
Zhu, Dahu
2024.
Model-enabled robotic machining framework for repairing paint film defects.
Robotics and Computer-Integrated Manufacturing,
Vol. 89,
Issue. ,
p.
102791.
Dong, Linjie
Zhang, Renfei
Wang, Junfei
Li, Jie
Wang, Shanshan
and
Wang, Xingsong
2024.
Research on the path planning algorithm and obstacle-crossing motion planning strategy for a cable trench inspection robot.
Robotica,
p.
1.
Chu, Liyang
Guo, Haifeng
and
Meng, Qingshi
2024.
Intelligent Logistics Vehicle Path Planning Using Fused Optimization Ant Colony Algorithm With Grid.
International Journal of Information Technologies and Systems Approach,
Vol. 17,
Issue. 1,
p.
1.
Wu, Chenhao
Fu, Xueliang
Li, Honghui
Hu, Hua
Li, Xue
and
Zhang, Liqian
2024.
A method based on improved ant colony algorithm feature selection combined with GWO-SVR model for predicting chlorophyll-a concentration in Wuliangsu Lake.
Water Science & Technology,
Vol. 89,
Issue. 1,
p.
20.
Yuan, Ke
Xu, Yanling
Wang, Xinghua
Ma, Xiaoyang
Wang, Qiang
and
Zhang, Huajun
2024.
Key technologies and research progress in robotic arc additive remanufacturing.
Sensors and Actuators A: Physical,
Vol. 376,
Issue. ,
p.
115547.
Peng, Weidong
Zhang, Yifan
and
Guo, Wei
2024.
Advances in Mechanical Design.
Vol. 155,
Issue. ,
p.
795.
Zhou, Rui
Liu, Manlu
Chen, Zhiliang
and
Li, Jinhao
2024.
3D Path Planning Digital Twins for Robot Arms Incorporating Reinforcement Learning.
p.
208.
Pan, Yuheng
Tao, Yixin
Lu, Weijia
Li, Guoyan
and
Cong, Jia
2024.
Dynamic Path Planning of Vehicles Based on the Adaptive Potential Field and Hierarchical Replacement Immune Algorithm.
Arabian Journal for Science and Engineering,
Vol. 49,
Issue. 9,
p.
12113.
Yu, Qiang
and
Zhou, Jun
2024.
A Review of Global and Local Path Planning Algorithms for Mobile Robots.
p.
84.
Dilli Babu, Guruswamy
Bala Chennaiah, Mallapuram
Siva Sankar, Dooba
and
Sivaji Babu, Kondapalli
2024.
Experimental investigation and optimization of IRB6700 ABB robot spot welding process parameters.
Materials Today: Proceedings,
Vol. 115,
Issue. ,
p.
53.
Wu, Shuai
Dong, Ani
Li, Qingxia
Wei, Wenhong
Zhang, Yuhui
and
Ye, Zijing
2024.
Application of ant colony optimization algorithm based on farthest point optimization and multi-objective strategy in robot path planning.
Applied Soft Computing,
Vol. 167,
Issue. ,
p.
112433.
Liu, Yunfeng
and
Wang, Lixin
2024.
AGV Path Planning: An Improved A* Algorithm Based on Bézier Curve Smoothing.
p.
243.
 $\alpha$
and
$\alpha$
and
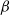 $\beta$
of the ant colony algorithm and as two-dimensional coordinates in the particle swarm algorithm. Finally, the simulation analysis was carried out using MATLAB to obtain the paths of the improved ant colony algorithm for six different sets of parameters with an average path length of 10,357.7509 mm, but the average path length obtained by conventional algorithm was 10,830.8394 mm. Convergence analysis of the improved ant colony algorithm showed that the average number of iterations was 17. Therefore, the improved ant colony algorithm has higher solution quality and converges faster.
$\beta$
of the ant colony algorithm and as two-dimensional coordinates in the particle swarm algorithm. Finally, the simulation analysis was carried out using MATLAB to obtain the paths of the improved ant colony algorithm for six different sets of parameters with an average path length of 10,357.7509 mm, but the average path length obtained by conventional algorithm was 10,830.8394 mm. Convergence analysis of the improved ant colony algorithm showed that the average number of iterations was 17. Therefore, the improved ant colony algorithm has higher solution quality and converges faster.