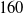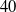Nomenclature
- H6A
Hybrid 6-Axis manipulator
- DoF
degree(s)-of-freedom
- FKP
forward kinematic problem
- IKP
inverse kinematic problem
- CAS
computer algebra system
- IKU
inverse kinematic univariate (polynomial/equation)
- DH
Denavit–Hartenberg (as in DH parameters, see ref. [Reference Ghosal1], pp. 43)
1. Introduction
Hybrid manipulators form a class of robots which incorporate some characteristics of both serial and parallel manipulators. The architecture of hybrid manipulators may vary significantly, for instance, it can consist of a sequential concatenation of serial and parallel modules (see, e.g., ref. [Reference Waldron, Raghavan and Roth2]) or several stages of parallel manipulators arranged in a series (as in ref. [Reference Shahinpoor3]) or a parallel combination of serial chains, forming closed kinematic loops (see, e.g., ref. [Reference Chablat, Wenger and Angeles4]). The main motivation of research into these manipulators is to attain some reasonable compromises between the serial characteristics, for example, large workspaces, and the parallel ones, for example, better payload-to-self-weight ratio, rigidity and superior dynamic response.
Many interesting manipulator architectures of hybrid nature have been proposed and analysed by various researchers in the last few decades. In one of the early works, Waldron et al. [Reference Waldron, Raghavan and Roth2] studied the kinematics of the ARTISAN hybrid manipulation system whose wrist and micro-manipulator together constitute a six-degrees-of-freedom (DoF) serial–parallel module. Spatial robots of six-DoF consisting of two 3-DoF parallel manipulators arranged serially have been analysed by Shahinpoor [Reference Shahinpoor3] and Tanev [Reference Tanev5]. Romdhane [Reference Romdhane6] introduced a novel six-DoF “hybrid serial-parallel Stewart like mechanism (HS-PM)”, which also has two 3-DoF parallel manipulators arranged serially. The forward kinematic problem (FKP) of a six-DoF hybrid manipulator with three identical limbs joining a moving platform to the fixed platform is presented in ref. [Reference Tahmasebi and Tsai7]. A two-limbed six-DoF hybrid manipulator, called the Hybrid 6-Axis Articulated Robot (H6AR), has been developed by Systemantics India Pvt. Ltd., Bangalore, and its kinematics has been analysed in ref. [Reference Rao and Raju8]. Chablat et al. [Reference Chablat, Wenger and Angeles4] have discussed the kinematic properties of a three-DoF hybrid manipulator capable of avoiding gain-type singularities. The stiffness characteristics of a novel hybrid manipulator called the Cassino Hybrid Manipulator (CaHyMan) has been investigated analytically in the closed form in ref. [Reference Carbone, Ceccarelli and Teolis9]. Forward kinematics of a serial chain of 3-UPS manipulators was analysed by means of screw theory in ref. [Reference Gallardo-Alvarado10]. Screw theory was employed in ref. [Reference Shi, Zhu and Li11] to study the forward kinematics of the hybrid manipulator IRB 260 developed by the company ABB, as well as the mobility of another six-DoF spatial hybrid manipulator in ref. [Reference Hu, Zhao and Cui12]. The latter manipulator, consisting of two spatial parallel manipulators in series, has been analysed recently by Hu et al. [Reference Hu, Huo, Gao and Zhang13] with regard to its inverse kinematics. Furthermore, the statics and stiffness characteristics of hybrid manipulators consisting of
![]() $k$
-stages of parallel manipulators arranged serially have been investigated by Hu et al. [Reference Hu, Yu, Lu, Sui and Han14].
$k$
-stages of parallel manipulators arranged serially have been investigated by Hu et al. [Reference Hu, Yu, Lu, Sui and Han14].
Several studies have been conducted on the kinematics of five-DoF hybrid manipulators designed as serial combinations of a three-DoF parallel manipulator and a two-DoF serial manipulator. For instance, Guo et al. [Reference Guo, Li, Cao and Gao15] have presented the closed-form kinematics of a novel hybrid manipulator, which consists of a 3T parallel module and a 2-R serial module. This 3T2R manipulator was modelled mathematically using Denavit–Hartenberg (DH) parameters. The inverse kinematics of a
![]() $2$
-R serial manipulator mounted on a 2R1T parallel manipulator is discussed in ref. [Reference Hu, Shi, Xu and Bai16]. Similarly, the forward and inverse kinematics of a combination of a 2-UPU parallel manipulator and a 2-R serial manipulator are studied in ref. [Reference Ye, Wang, Wu, Yue and Zhou17]. The forward and inverse kinematics of a 3T2R parallel–serial (hybrid) manipulator are presented in ref. [Reference Antonov, Fomin, Glazunov, Kiselev and Carbone18]. Yet another 5-axis hybrid robot, the TriMule, was analysed for its inverse kinematics and singularities in ref. [Reference Liu and Huang19].
$2$
-R serial manipulator mounted on a 2R1T parallel manipulator is discussed in ref. [Reference Hu, Shi, Xu and Bai16]. Similarly, the forward and inverse kinematics of a combination of a 2-UPU parallel manipulator and a 2-R serial manipulator are studied in ref. [Reference Ye, Wang, Wu, Yue and Zhou17]. The forward and inverse kinematics of a 3T2R parallel–serial (hybrid) manipulator are presented in ref. [Reference Antonov, Fomin, Glazunov, Kiselev and Carbone18]. Yet another 5-axis hybrid robot, the TriMule, was analysed for its inverse kinematics and singularities in ref. [Reference Liu and Huang19].
The applications of hybrid manipulators have also been as varied as their architectures. For instance, Yang et al. have presented closed-form symbolic solutions for both the forward and inverse kinematics of a new six-DoF hybrid manipulator with applications in deburring tasks for large jet-engine components in ref. [Reference Yang, Chen, Yeo and Lin20]. Xu et al. [Reference Xu, Cheung, Li, Ho and Zhang21] described the design of a hybrid manipulator, which is composed of a three-DoF parallel module, a two-DoF serial module and a redundant DoF, to aid in the process of computer-controlled ultra-precision free-form polishing. Inverse kinematic analysis of a new hybrid manipulator used for medical purposes was presented in ref. [Reference Kucuk and Gungor22]. This manipulator was formed by the serial combination of a three-DoF SCARA and a Stewart platform manipulator. Singh et al. [Reference Singh, Singla, Soni and Singla23] studied the kinematics of a seven-DoF spatial hybrid manipulator, meant to aid in surgery. Both the manipulators described in refs. [Reference Kucuk and Gungor22, Reference Singh, Singla, Soni and Singla23] were modelled using DH parameters.
This paper presents a detailed analysis of the kinematics of a novel six-DoF spatial hybrid manipulator, namely the Hybrid 6-Axis (H6A), developed by Systemantics India Pvt. Ltd., Bangalore. The manipulator consists of a pair of two-DoF serial arms arranged in parallel vertical planes (see Fig. 1). These are mounted on a rigid “waist”, which itself can rotate about a vertical axis fixed to the inertial frame of reference. At the other end, the arms are joined via a wrist assembly, thus creating a closed loop. At the wrist, the yaw and rollFootnote
1
DoFs are produced by the closed chain, while an actuator mounted on the wrist is responsible for a pitch motion, which is independent of the rest of the manipulator. The FKP and the inverse kinematic problem (IKP) of the manipulator are studied comprehensively in the closed form using extensive symbolic computations in a computer algebra system (CAS).Footnote
2
It is established that the solution to the FKP has eight branches (including the complex ones, if any) for a generic set of actuator inputs. Interestingly, even when all the branches are real, they manifest only as two identical sets of four poses
Footnote
3
physically, as a pair of distinct values of joint angles at the passive spherical joint on the right arm lead to the same configuration of the robot (see Fig. 2). The solution of the IKP turns out to be much more complicated and interesting, which involves the derivation and solution of a
![]() $40$
-degree univariate polynomial equation. For each solution of the said equation, there are four possible configurations of the manipulator (including the complex ones, as the case may be), thus leading to a total of
$40$
-degree univariate polynomial equation. For each solution of the said equation, there are four possible configurations of the manipulator (including the complex ones, as the case may be), thus leading to a total of
![]() $160$
solutions in the general case. The solution procedure is illustrated numerically, and the results thereof are validated by checking the residues of the original set of constraint equations, as well as comparing the solutions of IKP with the corresponding inputs of the forward kinematics. Singularities associated with the FKP and IKP are identified using the general condition of the merger of the branches of solutions. These are further analysed to identify the corresponding loss and gain of DoF(s) at the end-effector of the manipulator.
$160$
solutions in the general case. The solution procedure is illustrated numerically, and the results thereof are validated by checking the residues of the original set of constraint equations, as well as comparing the solutions of IKP with the corresponding inputs of the forward kinematics. Singularities associated with the FKP and IKP are identified using the general condition of the merger of the branches of solutions. These are further analysed to identify the corresponding loss and gain of DoF(s) at the end-effector of the manipulator.

Figure 1. Kinematic diagram of the H6A manipulator, showing the reference frames associated with the passive joints in additional close-ups.

Figure 2. Poses depicting the solutions to the forward kinematic problem for the given inputs (enumerated as per the rows of Table IV).
The key contributions of this paper may be summarised as follows.
The primary contribution of this work is to solve the kinematics of a hybrid manipulator with a novel architecture. The topology of H6A is unique, and any such “twin-handed” yet asymmetric hybrid architecture has not been analysed before, to the best of the authors’ knowledge. The nature of the analysis is exact and comprehensive, as opposed to numerical and consequently, partial. Due to the exact analytical nature of this work, the total number of solutions is conclusively established. The final results do not contain any spurious components and are, therefore, provably minimal. Furthermore, the symbolic nature of the kinematic analysis makes it easy to perform extensive analytical studies of the singularities. For example, a condition on the architecture parameters, which would lead to finite self-motion, was derived in the closed form (see Eq. (90)), along with other conditions for singularities.
A secondary contribution of the paper lies in the more generic field of symbolic computations. A number of techniques were developed and utilised in a fruitful manner to derive the analytical results presented in this paper (as detailed in Section 7). These techniques may be applied to any other problem in kinematics and beyond.
Finally, the integrated approach towards kinematics, which encompasses position and singularity analysis in the exact closed form, is a major contribution of this work, as its scope of application is not limited to this manipulator or even just hybrid manipulators – it could be applied to manipulators of any architecture, at least in principle. That it was applicable in the case of such a complex spatial hybrid manipulator establishes this claim in an objective manner.
The remainder of this paper is organised as follows: Section 2 presents the kinematic model of the manipulator, from the geometrical description of the manipulator to the derivation of the loop-closure equations. Sections 3 and 4 contain the detailed solution procedures of the FKP and IKP, respectively. Section 5 presents the numerical examples, including the validation of the results. The singularities of the manipulator mentioned above are studied in Section 6. The formulations and results presented in the paper are summarised in Section 7. Finally, the conclusions are presented in Section 8.
2. Kinematic model of the manipulator
The geometry of the H6A manipulator is described in this section, followed by the derivation of the loop-closure equations.
2.1. Geometry
The kinematic sketch of the H6A manipulator is shown in Fig. 1. The global frame of reference,
![]() ${\boldsymbol{{X}}}_0{\boldsymbol{{Y}}}_0{\boldsymbol{{Z}}}_0$
, is attached to the waist joint,
${\boldsymbol{{X}}}_0{\boldsymbol{{Y}}}_0{\boldsymbol{{Z}}}_0$
, is attached to the waist joint,
![]() ${\boldsymbol{{o}}}$
, which rotates about the
${\boldsymbol{{o}}}$
, which rotates about the
![]() ${\boldsymbol{{Z}}}_0$
axis. The robot manipulator is composed of a pair of 2-R “arms”,
${\boldsymbol{{Z}}}_0$
axis. The robot manipulator is composed of a pair of 2-R “arms”,
![]() ${\boldsymbol{{s}}}_L{\boldsymbol{{e}}}_L$
-
${\boldsymbol{{s}}}_L{\boldsymbol{{e}}}_L$
-
![]() ${\boldsymbol{{e}}}_L\boldsymbol{{p}}_L$
on the left and
${\boldsymbol{{e}}}_L\boldsymbol{{p}}_L$
on the left and
![]() ${\boldsymbol{{s}}}_R{\boldsymbol{{e}}}_R$
-
${\boldsymbol{{s}}}_R{\boldsymbol{{e}}}_R$
-
![]() ${\boldsymbol{{e}}}_R\boldsymbol{{p}}_R$
on the right, both of which are attached to the waist at a fixed offset
${\boldsymbol{{e}}}_R\boldsymbol{{p}}_R$
on the right, both of which are attached to the waist at a fixed offset
![]() $d_2$
from the centre of the waist,
$d_2$
from the centre of the waist,
![]() ${\boldsymbol{{o}}}$
. The left arm comprises an upper arm,
${\boldsymbol{{o}}}$
. The left arm comprises an upper arm,
![]() ${\boldsymbol{{s}}}_L{\boldsymbol{{e}}}_L$
, of length
${\boldsymbol{{s}}}_L{\boldsymbol{{e}}}_L$
, of length
![]() $l_2$
and a forearm,
$l_2$
and a forearm,
![]() ${\boldsymbol{{e}}}_L\boldsymbol{{p}}_L$
, of length
${\boldsymbol{{e}}}_L\boldsymbol{{p}}_L$
, of length
![]() $l_3$
. Similarly, the right arm consists of an upper arm,
$l_3$
. Similarly, the right arm consists of an upper arm,
![]() ${\boldsymbol{{s}}}_R{\boldsymbol{{e}}}_R$
, and a forearm,
${\boldsymbol{{s}}}_R{\boldsymbol{{e}}}_R$
, and a forearm,
![]() ${\boldsymbol{{e}}}_R\boldsymbol{{p}}_R$
, of lengths
${\boldsymbol{{e}}}_R\boldsymbol{{p}}_R$
, of lengths
![]() $l_2$
and
$l_2$
and
![]() $l_3$
, respectively. At the other end, the serial arms are connected together via a wrist assembly,
$l_3$
, respectively. At the other end, the serial arms are connected together via a wrist assembly,
![]() $\boldsymbol{{p}}_L$
-
$\boldsymbol{{p}}_L$
-
![]() ${\boldsymbol{{p}}}$
-
${\boldsymbol{{p}}}$
-
![]() $\boldsymbol{{p}}_R$
. The left arm is attached to the wrist assembly through a universal joint located at
$\boldsymbol{{p}}_R$
. The left arm is attached to the wrist assembly through a universal joint located at
![]() $\boldsymbol{{p}}_L$
. Likewise, a spherical at
$\boldsymbol{{p}}_L$
. Likewise, a spherical at
![]() ${\boldsymbol{{p}}}_R$
joins the right arm and the wrist assembly. The wrist assembly itself consists of two links of length
${\boldsymbol{{p}}}_R$
joins the right arm and the wrist assembly. The wrist assembly itself consists of two links of length
![]() $l_w$
, which connect each arm to a rotary joint located at the wrist point,
$l_w$
, which connect each arm to a rotary joint located at the wrist point,
![]() ${\boldsymbol{{p}}}$
. Additionally, an end-effector,
${\boldsymbol{{p}}}$
. Additionally, an end-effector,
![]() ${\boldsymbol{{e}}}$
, is connected to the rotary joint at
${\boldsymbol{{e}}}$
, is connected to the rotary joint at
![]() ${\boldsymbol{{p}}}$
, through an L-shaped link having proximal and distal arms of lengths
${\boldsymbol{{p}}}$
, through an L-shaped link having proximal and distal arms of lengths
![]() $a_6$
and
$a_6$
and
![]() $d_7$
, respectively. Thereafter, the L-shaped link is joined to the link
$d_7$
, respectively. Thereafter, the L-shaped link is joined to the link
![]() $\boldsymbol{{p}}_R\boldsymbol{{p}}$
at an angle
$\boldsymbol{{p}}_R\boldsymbol{{p}}$
at an angle
![]() $\kappa$
. While the closed loop
$\kappa$
. While the closed loop
![]() ${\boldsymbol{{o}}}$
-
${\boldsymbol{{o}}}$
-
![]() ${\boldsymbol{{s}}}_L$
-
${\boldsymbol{{s}}}_L$
-
![]() ${\boldsymbol{{e}}}_L$
-
${\boldsymbol{{e}}}_L$
-
![]() $\boldsymbol{{p}}_L$
-
$\boldsymbol{{p}}_L$
-
![]() ${\boldsymbol{{p}}}$
-
${\boldsymbol{{p}}}$
-
![]() $\boldsymbol{{p}}_R$
-
$\boldsymbol{{p}}_R$
-
![]() ${\boldsymbol{{e}}}_R$
-
${\boldsymbol{{e}}}_R$
-
![]() ${\boldsymbol{{s}}}_R$
-
${\boldsymbol{{s}}}_R$
-
![]() ${\boldsymbol{{o}}}$
is responsible for the yaw and roll motions at the end-effector, a revolute actuator placed right before the end-effector is responsible for the pitch motion which is decoupled from the rest of the motions of the manipulator.
${\boldsymbol{{o}}}$
is responsible for the yaw and roll motions at the end-effector, a revolute actuator placed right before the end-effector is responsible for the pitch motion which is decoupled from the rest of the motions of the manipulator.
The waist joint at
![]() ${\boldsymbol{{o}}}$
, shoulder joints at
${\boldsymbol{{o}}}$
, shoulder joints at
![]() ${\boldsymbol{{s}}}_L$
and
${\boldsymbol{{s}}}_L$
and
![]() ${\boldsymbol{{s}}}_R$
, elbow joints at
${\boldsymbol{{s}}}_R$
, elbow joints at
![]() ${\boldsymbol{{e}}}_L$
and
${\boldsymbol{{e}}}_L$
and
![]() ${\boldsymbol{{e}}}_R$
and the revolute joint situated before the end-effector,
${\boldsymbol{{e}}}_R$
and the revolute joint situated before the end-effector,
![]() ${\boldsymbol{{e}}}$
, are active (i.e., actuated), and the corresponding joint angles are denoted by
${\boldsymbol{{e}}}$
, are active (i.e., actuated), and the corresponding joint angles are denoted by
![]() $\theta _1$
,
$\theta _1$
,
![]() $\theta _{2L}$
,
$\theta _{2L}$
,
![]() $\theta _{2R}$
,
$\theta _{2R}$
,
![]() $\theta _{3L}$
,
$\theta _{3L}$
,
![]() $\theta _{3R}$
and
$\theta _{3R}$
and
![]() $\theta _7$
, respectively. These joints account for the six-DoF of the end-effector.Footnote
4
On the other hand, the joints associated with the wrist assembly, that is, those located at
$\theta _7$
, respectively. These joints account for the six-DoF of the end-effector.Footnote
4
On the other hand, the joints associated with the wrist assembly, that is, those located at
![]() ${\boldsymbol{{p}}}_L$
,
${\boldsymbol{{p}}}_L$
,
![]() $\boldsymbol{{p}}$
and
$\boldsymbol{{p}}$
and
![]() ${\boldsymbol{{p}}}_R$
, respectively, are passive (i.e., unactuated), and the corresponding joint angles are
${\boldsymbol{{p}}}_R$
, respectively, are passive (i.e., unactuated), and the corresponding joint angles are
![]() $\{\phi _{4L}, \phi _{5L}\}$
,
$\{\phi _{4L}, \phi _{5L}\}$
,
![]() $\phi _{6L}$
and
$\phi _{6L}$
and
![]() $\{\phi _{4R}, \phi _{5R}, \phi _{6R}\}$
, respectively. Figure 1 shows the references for all the pertinent joint angles. For instance, the angle
$\{\phi _{4R}, \phi _{5R}, \phi _{6R}\}$
, respectively. Figure 1 shows the references for all the pertinent joint angles. For instance, the angle
![]() $\theta _1$
is measured as the angle between
$\theta _1$
is measured as the angle between
![]() $\mathbf{X}_0$
and
$\mathbf{X}_0$
and
![]() $\boldsymbol{{x}}_1$
, measured about
$\boldsymbol{{x}}_1$
, measured about
![]() $\mathbf{Z}_0$
. Similarly,
$\mathbf{Z}_0$
. Similarly,
![]() $\theta _7$
is the angle that
$\theta _7$
is the angle that
![]() $\boldsymbol{{x}}_e$
makes with (a line parallel to)
$\boldsymbol{{x}}_e$
makes with (a line parallel to)
![]() $\boldsymbol{{x}}_{7L}$
. The close-ups of the wrist in Fig. 1 depict the framesFootnote
5
associated with the universal joint at
$\boldsymbol{{x}}_{7L}$
. The close-ups of the wrist in Fig. 1 depict the framesFootnote
5
associated with the universal joint at
![]() $\boldsymbol{{p}}_L$
and spherical joint
$\boldsymbol{{p}}_L$
and spherical joint
![]() $\boldsymbol{{p}}_R$
. The intermediate frames at the spherical joint are omitted to avoid clutter. The rotation at the spherical joint
$\boldsymbol{{p}}_R$
. The intermediate frames at the spherical joint are omitted to avoid clutter. The rotation at the spherical joint
![]() $\boldsymbol{{p}}_R$
, between the frames
$\boldsymbol{{p}}_R$
, between the frames
![]() $\boldsymbol{{x}}_{4R}\boldsymbol{{z}}_{4R}\boldsymbol{{y}}_{4R}$
and
$\boldsymbol{{x}}_{4R}\boldsymbol{{z}}_{4R}\boldsymbol{{y}}_{4R}$
and
![]() $\boldsymbol{{x}}_{7R}\boldsymbol{{y}}_{7R}\boldsymbol{{z}}_{7R}$
(the axes
$\boldsymbol{{x}}_{7R}\boldsymbol{{y}}_{7R}\boldsymbol{{z}}_{7R}$
(the axes
![]() $\boldsymbol{{y}}_{4R},\boldsymbol{{y}}_{7R}$
being omitted in the figure) may be represented using the
$\boldsymbol{{y}}_{4R},\boldsymbol{{y}}_{7R}$
being omitted in the figure) may be represented using the
![]() $\mathbf{Z}\mathbf{X}\mathbf{Z}$
convention of Euler angles as
$\mathbf{Z}\mathbf{X}\mathbf{Z}$
convention of Euler angles as
![]() $\mathbf{R}_Z(\phi _{4R})\mathbf{R}_X(\phi _{5R})\mathbf{R}_Z(\phi _{6R}+\pi/2)$
. In summary, the H6A manipulator has a total of seven architecture parameters, namely
$\mathbf{R}_Z(\phi _{4R})\mathbf{R}_X(\phi _{5R})\mathbf{R}_Z(\phi _{6R}+\pi/2)$
. In summary, the H6A manipulator has a total of seven architecture parameters, namely
![]() $\{d_2, l_2, l_3, l_w, a_6, d_7, \kappa \}$
, and six actuated joints represented by the active angles,
$\{d_2, l_2, l_3, l_w, a_6, d_7, \kappa \}$
, and six actuated joints represented by the active angles,
![]() $\boldsymbol{\theta } = [\theta _1, \theta _{2L}, \theta _{2R}, \theta _{3L}, \theta _{3R}, \theta _7]^\top$
. In addition, there are six joints represented by the passive angles,
$\boldsymbol{\theta } = [\theta _1, \theta _{2L}, \theta _{2R}, \theta _{3L}, \theta _{3R}, \theta _7]^\top$
. In addition, there are six joints represented by the passive angles,
![]() $\boldsymbol{\phi } = [\phi _{4L}, \phi _{4R}, \phi _{5L}, \phi _{5R}, \phi _{6L}, \phi _{6R}]^\top$
. The left kinematic chain of the manipulator starts at the waist,
$\boldsymbol{\phi } = [\phi _{4L}, \phi _{4R}, \phi _{5L}, \phi _{5R}, \phi _{6L}, \phi _{6R}]^\top$
. The left kinematic chain of the manipulator starts at the waist,
![]() ${\boldsymbol{{o}}}$
, and runs all the way to the end-effector,
${\boldsymbol{{o}}}$
, and runs all the way to the end-effector,
![]() ${\boldsymbol{{e}}}$
, via the left elbow; it is designated as
${\boldsymbol{{e}}}$
, via the left elbow; it is designated as
![]() ${\boldsymbol{{o}}}\textrm{-}{\boldsymbol{{s}}}_L$
-
${\boldsymbol{{o}}}\textrm{-}{\boldsymbol{{s}}}_L$
-
![]() ${\boldsymbol{{e}}}_L$
-
${\boldsymbol{{e}}}_L$
-
![]() $\boldsymbol{{p}}_L$
-
$\boldsymbol{{p}}_L$
-
![]() ${\boldsymbol{{p}}}$
-
${\boldsymbol{{p}}}$
-
![]() ${\boldsymbol{{e}}}$
. Similarly, the right chain, running from
${\boldsymbol{{e}}}$
. Similarly, the right chain, running from
![]() ${\boldsymbol{{o}}}$
to
${\boldsymbol{{o}}}$
to
![]() $\boldsymbol{{p}}$
, is designated as
$\boldsymbol{{p}}$
, is designated as
![]() ${{\boldsymbol{{o}}}}\textrm{-}{{\boldsymbol{{s}}}}_R\textrm{-}\boldsymbol{{p}}\textrm{-}{{\boldsymbol{{e}}}}_R\textrm{-}\boldsymbol{{p}}_R\textrm{-}\boldsymbol{{p}}$
. In order to keep the kinematic descriptions of these chains simple and generic, these are described via the DH parameters (see, e.g., ref. [Reference Ghosal1], pp. 43) owing primarily to the universal popularity of this system. The left and right chains are described in Tables I and II, respectively.Footnote
6
Further, from these tables, two sequences of
${{\boldsymbol{{o}}}}\textrm{-}{{\boldsymbol{{s}}}}_R\textrm{-}\boldsymbol{{p}}\textrm{-}{{\boldsymbol{{e}}}}_R\textrm{-}\boldsymbol{{p}}_R\textrm{-}\boldsymbol{{p}}$
. In order to keep the kinematic descriptions of these chains simple and generic, these are described via the DH parameters (see, e.g., ref. [Reference Ghosal1], pp. 43) owing primarily to the universal popularity of this system. The left and right chains are described in Tables I and II, respectively.Footnote
6
Further, from these tables, two sequences of
![]() $4\times 4$
homogeneous transformation matrices, namely
$4\times 4$
homogeneous transformation matrices, namely
![]() ${}^{0}_{1}{{{\boldsymbol{{T}}}}},\dots,{}^{7}_{8}{{{\boldsymbol{{T}}}}}_L$
and
${}^{0}_{1}{{{\boldsymbol{{T}}}}},\dots,{}^{7}_{8}{{{\boldsymbol{{T}}}}}_L$
and
![]() ${}^{0}_{1}{{{\boldsymbol{{T}}}}},\dots,{}^{7}_{8}{{{\boldsymbol{{T}}}}}_R$
, are generated in a systematic manner, which are subsequently used in Section 2.2 to formulate the loop-closure equations of the manipulator.
${}^{0}_{1}{{{\boldsymbol{{T}}}}},\dots,{}^{7}_{8}{{{\boldsymbol{{T}}}}}_R$
, are generated in a systematic manner, which are subsequently used in Section 2.2 to formulate the loop-closure equations of the manipulator.
Table I. DH parameters for the left chain of the H6A manipulator.

Table II. DH parameters for the right chain of the H6A manipulator.

It may be noted here that the architecture of the H6A is unique in the sense that it resembles two hands emanating separately from a single-DoF “waist”, which are brought back together at the wrist assembly. An additional and independently actuated link attached to the wrist assembly constitutes the final output. The remaining four-DoF appear in the portion of the manipulator where the two arms are not connected to each other. As such, it may be but natural to expect that these parts of the two arms, that is,
![]() ${{\boldsymbol{{s}}}}_L\textrm{-}{{\boldsymbol{{e}}}}_L\textrm{-}\boldsymbol{{p}}_L$
and
${{\boldsymbol{{s}}}}_L\textrm{-}{{\boldsymbol{{e}}}}_L\textrm{-}\boldsymbol{{p}}_L$
and
![]() ${{\boldsymbol{{s}}}}_R\textrm{-}{{\boldsymbol{{e}}}}_R\textrm{-}\boldsymbol{{p}}_R$
, should be identical in their architecture, inclusive of the manner at which they meet the wrist assembly. Indeed, this thought process seems to have led to the design of the manipulator H6AR, introduced in ref. [Reference Rao and Raju8], which preceded the manipulator H6A. However, the output DoF of the H6AR manipulator, based on its architecture, is seen to be five, that is, given its six actuators, the manipulator is redundantly actuated. The design of H6A eliminates this problem by replacing one of the two universal joints connecting the arms to the wrist assembly by a spherical joint (at
${{\boldsymbol{{s}}}}_R\textrm{-}{{\boldsymbol{{e}}}}_R\textrm{-}\boldsymbol{{p}}_R$
, should be identical in their architecture, inclusive of the manner at which they meet the wrist assembly. Indeed, this thought process seems to have led to the design of the manipulator H6AR, introduced in ref. [Reference Rao and Raju8], which preceded the manipulator H6A. However, the output DoF of the H6AR manipulator, based on its architecture, is seen to be five, that is, given its six actuators, the manipulator is redundantly actuated. The design of H6A eliminates this problem by replacing one of the two universal joints connecting the arms to the wrist assembly by a spherical joint (at
![]() $\boldsymbol{{p}}_R$
, to be specific), while retaining the symmetry in the rest of the architecture, as well as in the dimensions of the individual links.Footnote
7
Evidently, this asymmetric architecture leads to interesting kinematic behaviours, as may be seen in Section 4, in particular.
$\boldsymbol{{p}}_R$
, to be specific), while retaining the symmetry in the rest of the architecture, as well as in the dimensions of the individual links.Footnote
7
Evidently, this asymmetric architecture leads to interesting kinematic behaviours, as may be seen in Section 4, in particular.
2.2. Loop-closure equations
The loop-closure equations are constraints which ensure that the manipulator maintains its kinematic integrity at every configuration. For the manipulator at hand, these equations are formulated by equating the pose of the wrist point
![]() $\boldsymbol{{p}}$
calculated through the left chain with that from the right. Hence, the transformation matrix
$\boldsymbol{{p}}$
calculated through the left chain with that from the right. Hence, the transformation matrix
![]() ${}^{0}_{p}{{\boldsymbol{{T}}}}\in{\mathbb{SE}(3)}$
is determined as a concatenation of the matrices in constituting the second column of Table I using the left chain (see, e.g., ref. [Reference Ghosal1], pp. 48):
${}^{0}_{p}{{\boldsymbol{{T}}}}\in{\mathbb{SE}(3)}$
is determined as a concatenation of the matrices in constituting the second column of Table I using the left chain (see, e.g., ref. [Reference Ghosal1], pp. 48):
The matrix
![]() ${}^{0}_{p}{{\boldsymbol{{T}}}}$
may also be computed considering the right chain (refer to Table II):
${}^{0}_{p}{{\boldsymbol{{T}}}}$
may also be computed considering the right chain (refer to Table II):
Therefore, the loop-closure constraints are obtained by equating the expressions of
![]() ${}^{0}_{p}{{\boldsymbol{{T}}}}$
appearing in Eqs. (1) and (2) and eliminating the common factor,
${}^{0}_{p}{{\boldsymbol{{T}}}}$
appearing in Eqs. (1) and (2) and eliminating the common factor,
![]() ${}^{0}_{1}{{\boldsymbol{{T}}}}$
, between them:
${}^{0}_{1}{{\boldsymbol{{T}}}}$
, between them:
Equation (3) contains six independent scalar equations, which form the loop-closure equations of the manipulator. The six unknown passive joint angles,
![]() $\boldsymbol{\phi }$
, are solved in terms of the active joint angles,
$\boldsymbol{\phi }$
, are solved in terms of the active joint angles,
![]() $\boldsymbol{\theta }$
, in the next section.
$\boldsymbol{\theta }$
, in the next section.
3. Forward kinematics
The FKP is defined as the determination of the poses of end-effector of the H6A manipulator, as represented via:
for a given set of active joint angle inputs,
![]() $\boldsymbol{\theta }$
. It involves an intermediary step of solving for the passive joint angle variables,
$\boldsymbol{\theta }$
. It involves an intermediary step of solving for the passive joint angle variables,
![]() $\boldsymbol{\phi }$
, in terms of the active joint angle inputs,
$\boldsymbol{\phi }$
, in terms of the active joint angle inputs,
![]() $\boldsymbol{\theta }$
.
$\boldsymbol{\theta }$
.
Firstly, the loop-closure constraint, (3), is rearranged to obtain the passive joint angle variables corresponding to the left chain, grouped together as
![]() $\boldsymbol{\phi }_L=[\phi _{4L}, \phi _{5L}, \phi _{6L}]^\top$
:
$\boldsymbol{\phi }_L=[\phi _{4L}, \phi _{5L}, \phi _{6L}]^\top$
:
Subsequently, equating the displacement vectors (i.e., the first three rows of the fourth column) on both sides of (5) yields
 \begin{align} &\boldsymbol{\eta }_{FKL} \,{:\!=}\, 2 l_w \sin \frac{\phi _{6L}}{2} \begin{bmatrix} &\hspace{-0.1cm}-\sin \phi _{4L} \sin \left (\phi _{5L} + \dfrac{\phi _{6L}}{2}\right ) \\ \\[-9pt] &\hspace{-0.1cm}\cos \phi _{4L} \sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right )\\ \\[-9pt] &\hspace{-0.1cm}-\cos \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right ) \end{bmatrix} - \begin{bmatrix} l_{13}\\ \\[-9pt] l_{23}\\ \\[-9pt] l_{33} \end{bmatrix}=\textbf{0}, \; \textrm{where:}\nonumber \\[3pt] &\alpha _1=\theta _{2L}-\theta _{2R}+\theta _{3L}-\theta _{3R}, \nonumber \\[3pt] &l_{13} = - l_2 \sin \theta _{3L} + l_2 \sin (\alpha _1 + \theta _{3R}) + l_3 \sin \alpha _1,\nonumber \\[3pt] &l_{23} = 2 d_2,\nonumber \\[3pt] &l_{33} = - l_2 \cos \theta _{3L} + l_2 \cos (\alpha _1 + \theta _{3R}) - l_3 (1 - \cos \alpha _1). \end{align}
\begin{align} &\boldsymbol{\eta }_{FKL} \,{:\!=}\, 2 l_w \sin \frac{\phi _{6L}}{2} \begin{bmatrix} &\hspace{-0.1cm}-\sin \phi _{4L} \sin \left (\phi _{5L} + \dfrac{\phi _{6L}}{2}\right ) \\ \\[-9pt] &\hspace{-0.1cm}\cos \phi _{4L} \sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right )\\ \\[-9pt] &\hspace{-0.1cm}-\cos \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right ) \end{bmatrix} - \begin{bmatrix} l_{13}\\ \\[-9pt] l_{23}\\ \\[-9pt] l_{33} \end{bmatrix}=\textbf{0}, \; \textrm{where:}\nonumber \\[3pt] &\alpha _1=\theta _{2L}-\theta _{2R}+\theta _{3L}-\theta _{3R}, \nonumber \\[3pt] &l_{13} = - l_2 \sin \theta _{3L} + l_2 \sin (\alpha _1 + \theta _{3R}) + l_3 \sin \alpha _1,\nonumber \\[3pt] &l_{23} = 2 d_2,\nonumber \\[3pt] &l_{33} = - l_2 \cos \theta _{3L} + l_2 \cos (\alpha _1 + \theta _{3R}) - l_3 (1 - \cos \alpha _1). \end{align}
The forward kinematic univariate equation, in
![]() $\phi _{6L}$
, may be obtained as:
$\phi _{6L}$
, may be obtained as:
Equation (7) yields, in general, four distinct values of
![]() $\dfrac{\phi _{6L}}{2}$
, given by:
$\dfrac{\phi _{6L}}{2}$
, given by:
 \begin{align} &\frac{\phi _{6L}}{2} = \arcsin{\left ( \frac{\pm \sqrt{l_{13}^2+l_{23}^2+l_{33}^2}}{2 l_w}\right )}, \quad \pi - \arcsin{\left ( \frac{\pm \sqrt{l_{13}^2+l_{23}^2+l_{33}^2}}{2 l_w}\right )}, \;\textrm{since}\ \ l_w\neq 0. \end{align}
\begin{align} &\frac{\phi _{6L}}{2} = \arcsin{\left ( \frac{\pm \sqrt{l_{13}^2+l_{23}^2+l_{33}^2}}{2 l_w}\right )}, \quad \pi - \arcsin{\left ( \frac{\pm \sqrt{l_{13}^2+l_{23}^2+l_{33}^2}}{2 l_w}\right )}, \;\textrm{since}\ \ l_w\neq 0. \end{align}
However, these solutions coalesce into only a pair of distinct solutions for
![]() $\phi _{6L}$
(since
$\phi _{6L}$
(since
![]() $2\pi \pm \psi \equiv \pm \psi$
,
$2\pi \pm \psi \equiv \pm \psi$
,
![]() $ \forall \psi \in [0, 2\pi ]$
):
$ \forall \psi \in [0, 2\pi ]$
):
 \begin{align} &{\phi _{6L} =\pm 2\arcsin{\left (\frac{ \sqrt{l_{13}^2+l_{23}^2+l_{33}^2}}{2 l_w}\right )}.} \end{align}
\begin{align} &{\phi _{6L} =\pm 2\arcsin{\left (\frac{ \sqrt{l_{13}^2+l_{23}^2+l_{33}^2}}{2 l_w}\right )}.} \end{align}
The remaining unknowns in (6) are obtained as:Footnote 8
 \begin{align}\phi _{5L} = \operatorname{atan2}\left ( \frac{\pm \sqrt{l_{13}^2+l_{23}^2}}{2 l_w \sin \dfrac{\phi _{6L}}{2}}, \dfrac{-l_{33}}{ 2 l_w \sin \dfrac{\phi _{6L}}{2}}\right ) - \frac{\phi _{6L}}{2}, \;\textrm{assuming} \sin \frac{\phi _{6L}}{2}\neq 0 ; \end{align}
\begin{align}\phi _{5L} = \operatorname{atan2}\left ( \frac{\pm \sqrt{l_{13}^2+l_{23}^2}}{2 l_w \sin \dfrac{\phi _{6L}}{2}}, \dfrac{-l_{33}}{ 2 l_w \sin \dfrac{\phi _{6L}}{2}}\right ) - \frac{\phi _{6L}}{2}, \;\textrm{assuming} \sin \frac{\phi _{6L}}{2}\neq 0 ; \end{align}
 \begin{align} \phi _{4L} &= \operatorname{atan2}\left (\frac{-l_{13}}{2 l_w \sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2} \right ) \sin \dfrac{\phi _{6L}}{2}}, \frac{l_{23}}{2 l_w \sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right )\sin \dfrac{\phi _{6L}}{2}} \right ), \nonumber \\ &\quad \textrm{assuming further:}\ \sin \left (\phi _{5L}+\frac{\phi _{6L}}{2}\right ) \neq 0. \end{align}
\begin{align} \phi _{4L} &= \operatorname{atan2}\left (\frac{-l_{13}}{2 l_w \sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2} \right ) \sin \dfrac{\phi _{6L}}{2}}, \frac{l_{23}}{2 l_w \sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right )\sin \dfrac{\phi _{6L}}{2}} \right ), \nonumber \\ &\quad \textrm{assuming further:}\ \sin \left (\phi _{5L}+\frac{\phi _{6L}}{2}\right ) \neq 0. \end{align}
It may be observed from Eqs. (9)–(11) that there are four
Footnote
9
distinct sets of solutions for the passive joint angles
![]() $\boldsymbol{\phi }_L$
for a generic input. However, under special conditions these solutions can merge, for example, when
$\boldsymbol{\phi }_L$
for a generic input. However, under special conditions these solutions can merge, for example, when
![]() $l_{13}^2+ l_{23}^2+ l_{33}^2=0 \Rightarrow \sin \dfrac{\phi _{6L}}{2}=0$
, or
$l_{13}^2+ l_{23}^2+ l_{33}^2=0 \Rightarrow \sin \dfrac{\phi _{6L}}{2}=0$
, or
![]() $l_{13}^2+l_{23}^2= 0 \Rightarrow \sin \left(\phi _{5L}+ \dfrac{\phi _{6L}}{2}\right)= 0$
, Eqs. (9) and (10) have repeated real solutions due to the coalescence of pairs of real or complex conjugate solutions, which then manifest as pairs of coincident real solutions, thus forming the boundaries between the real and complex solutions. These singular cases are discussed in Case 1 in Section 6.1.
$l_{13}^2+l_{23}^2= 0 \Rightarrow \sin \left(\phi _{5L}+ \dfrac{\phi _{6L}}{2}\right)= 0$
, Eqs. (9) and (10) have repeated real solutions due to the coalescence of pairs of real or complex conjugate solutions, which then manifest as pairs of coincident real solutions, thus forming the boundaries between the real and complex solutions. These singular cases are discussed in Case 1 in Section 6.1.
The unknown passive joint variables associated with the right arm, namely
![]() $\boldsymbol{\phi }_R=[\phi _{4R}, \phi _{5R}, \phi _{6R}]^\top$
, are solved in a manner similar to the analysis of the left arm described above. First, the loop-closure equation, (3), is rearranged as:
$\boldsymbol{\phi }_R=[\phi _{4R}, \phi _{5R}, \phi _{6R}]^\top$
, are solved in a manner similar to the analysis of the left arm described above. First, the loop-closure equation, (3), is rearranged as:
Thereafter, equating elements
![]() $(1,3)$
,
$(1,3)$
,
![]() $(2,3)$
,
$(2,3)$
,
![]() $(3,1)$
,
$(3,1)$
,
![]() $(3,2)$
and
$(3,2)$
and
![]() $(3,3)$
of the transformation matrices (where element
$(3,3)$
of the transformation matrices (where element
![]() $(i,j)$
appears in the ith row and the jth column of a matrix) appearing on either side of (12), one obtains
$(i,j)$
appears in the ith row and the jth column of a matrix) appearing on either side of (12), one obtains
 \begin{align} &{\boldsymbol{\eta }_{FKR} \,{:\!=}\, \left[\begin{array}{c@{\quad}c}&\sin \phi _{4R} \sin \phi _{5R}\\ \\[-9pt] &\hspace{-0.1cm}-\cos \phi _{4R} \sin \phi _{5R}\\ \\[-9pt] &\hspace{-0.1cm}\cos \phi _{5R}\\ \\[-9pt] &\hspace{-0.1cm}\cos \phi _{6R} \sin \phi _{5R}\\ \\[-9pt] &\hspace{-0.1cm}-\sin \phi _{6R} \sin \phi _{5R} \end{array}\right] - \begin{bmatrix} r_{13}\\ \\[-9pt] r_{23}\\ \\[-9pt] r_{33}\\ \\[-9pt] r_{31}\\ \\[-9pt] r_{32} \end{bmatrix}=\textbf{0}, \; \textrm{where:}} \end{align}
\begin{align} &{\boldsymbol{\eta }_{FKR} \,{:\!=}\, \left[\begin{array}{c@{\quad}c}&\sin \phi _{4R} \sin \phi _{5R}\\ \\[-9pt] &\hspace{-0.1cm}-\cos \phi _{4R} \sin \phi _{5R}\\ \\[-9pt] &\hspace{-0.1cm}\cos \phi _{5R}\\ \\[-9pt] &\hspace{-0.1cm}\cos \phi _{6R} \sin \phi _{5R}\\ \\[-9pt] &\hspace{-0.1cm}-\sin \phi _{6R} \sin \phi _{5R} \end{array}\right] - \begin{bmatrix} r_{13}\\ \\[-9pt] r_{23}\\ \\[-9pt] r_{33}\\ \\[-9pt] r_{31}\\ \\[-9pt] r_{32} \end{bmatrix}=\textbf{0}, \; \textrm{where:}} \end{align}
 \begin{align*} &\begin{aligned} \nonumber \beta _1 =& \phi _{5L} + \phi _{6L},\\ \nonumber r_{13}=&\frac{1}{4} (\!\cos \left (\alpha _1+\phi _{4L}-\beta _1\right )-\cos \left (\alpha _1-\phi _{4L}-\beta _1\right ) +\cos \left (\alpha _1-\phi _{4L}+\beta _1\right )-\cos \left (\alpha _1+\phi _{4L}+\beta _1\right )\\ \nonumber &-2 \sin \left (\alpha _1-\beta _1\right )+2 \sin \left (\alpha _1+\beta _1\right )),\\ \nonumber r_{23}=&-\cos \phi _{4L}\sin \beta _1,\\ \nonumber r_{33}=&\frac{1}{2} (\!\cos \left (\alpha _1-\beta _1\right )+\cos \left (\alpha _1+\beta _1\right ) +2 \sin \alpha _1 \sin \phi _{4L} \sin \beta _1),\\ \nonumber r_{31}=&\frac{1}{4} (\!\cos \left (\alpha _1+\phi _{4L}-\beta _1\right )-\cos \left (\alpha _1-\phi _{4L}-\beta _1\right )-\cos \left (\alpha _1-\phi _{4L}+\beta _1\right )+\cos \left (\alpha _1+\phi _{4L}+\beta _1\right )\\ \nonumber &-2 \sin \left (\alpha _1-\beta _1\right )+2 \sin \left (\alpha _1+\beta _1\right )),\\ \nonumber r_{32}=&-\cos \phi _{4L}\sin \alpha _1. \end{aligned} \end{align*}
\begin{align*} &\begin{aligned} \nonumber \beta _1 =& \phi _{5L} + \phi _{6L},\\ \nonumber r_{13}=&\frac{1}{4} (\!\cos \left (\alpha _1+\phi _{4L}-\beta _1\right )-\cos \left (\alpha _1-\phi _{4L}-\beta _1\right ) +\cos \left (\alpha _1-\phi _{4L}+\beta _1\right )-\cos \left (\alpha _1+\phi _{4L}+\beta _1\right )\\ \nonumber &-2 \sin \left (\alpha _1-\beta _1\right )+2 \sin \left (\alpha _1+\beta _1\right )),\\ \nonumber r_{23}=&-\cos \phi _{4L}\sin \beta _1,\\ \nonumber r_{33}=&\frac{1}{2} (\!\cos \left (\alpha _1-\beta _1\right )+\cos \left (\alpha _1+\beta _1\right ) +2 \sin \alpha _1 \sin \phi _{4L} \sin \beta _1),\\ \nonumber r_{31}=&\frac{1}{4} (\!\cos \left (\alpha _1+\phi _{4L}-\beta _1\right )-\cos \left (\alpha _1-\phi _{4L}-\beta _1\right )-\cos \left (\alpha _1-\phi _{4L}+\beta _1\right )+\cos \left (\alpha _1+\phi _{4L}+\beta _1\right )\\ \nonumber &-2 \sin \left (\alpha _1-\beta _1\right )+2 \sin \left (\alpha _1+\beta _1\right )),\\ \nonumber r_{32}=&-\cos \phi _{4L}\sin \alpha _1. \end{aligned} \end{align*}
The passive joint angles
![]() $\boldsymbol{\phi }_L$
have been obtained previously, as in Eqs. (9)–(11). Taking these into cognisance, the solutions of passive angles
$\boldsymbol{\phi }_L$
have been obtained previously, as in Eqs. (9)–(11). Taking these into cognisance, the solutions of passive angles
![]() $\boldsymbol{\phi }_R$
from (13) are computed as:
$\boldsymbol{\phi }_R$
from (13) are computed as:
Equations (14)–(16) show that the passive joint angles
![]() $\boldsymbol{\phi }_R$
have two solutions for a generic set of passive joint angles
$\boldsymbol{\phi }_R$
have two solutions for a generic set of passive joint angles
![]() $\boldsymbol{\phi }_L$
. These solutions merge when
$\boldsymbol{\phi }_L$
. These solutions merge when
![]() $r_{31}^2+r_{32}^2=0 \Rightarrow \sin \phi _{5R}=0$
, (14) produces repeated roots. This singularity is studied in Case 2 of Section 6.1.
$r_{31}^2+r_{32}^2=0 \Rightarrow \sin \phi _{5R}=0$
, (14) produces repeated roots. This singularity is studied in Case 2 of Section 6.1.
After computing the solutions of
![]() $\boldsymbol{\phi }_L$
from Eqs. (9)–(11) and those of
$\boldsymbol{\phi }_L$
from Eqs. (9)–(11) and those of
![]() $\boldsymbol{\phi }_R$
from Eqs. (14)–(16), the configurations of all the links may be ascertained from the link-transformation matrices given in Tables I and II, thus completing the solution of the FKP. The total number of solutions to the FKP for any generic input equals
$\boldsymbol{\phi }_R$
from Eqs. (14)–(16), the configurations of all the links may be ascertained from the link-transformation matrices given in Tables I and II, thus completing the solution of the FKP. The total number of solutions to the FKP for any generic input equals
![]() $4\times 2 = 8$
(see Table IV and Fig. 2 in Section 5.1).
$4\times 2 = 8$
(see Table IV and Fig. 2 in Section 5.1).
The solution procedure for the IKP is presented in the following section.
4. Inverse kinematics
The IKP involves the determination of the active joint angles,
![]() $\boldsymbol{\theta }$
, along with the passive joint angles,
$\boldsymbol{\theta }$
, along with the passive joint angles,
![]() $\boldsymbol{\phi }$
, for a given pose of the end-effector of the H6A manipulator, as represented by the matrix
$\boldsymbol{\phi }$
, for a given pose of the end-effector of the H6A manipulator, as represented by the matrix
![]() ${}^{0}_{e}{{\boldsymbol{{T}}}}$
${}^{0}_{e}{{\boldsymbol{{T}}}}$
![]() $\in$
$\in$
![]() $\mathbb{SE}(3)$
. The task-space coordinates are input in the form of a displacement vector,
$\mathbb{SE}(3)$
. The task-space coordinates are input in the form of a displacement vector,
![]() $\boldsymbol{{p}}=[p_x, p_y, p_z]^\top$
, and three Euler angles, namely
$\boldsymbol{{p}}=[p_x, p_y, p_z]^\top$
, and three Euler angles, namely
![]() $\{\alpha, \beta, \gamma \}$
, representing the orientation of the end-effector in the ZYZ convention, leading to the following parametrisation of the task space:
$\{\alpha, \beta, \gamma \}$
, representing the orientation of the end-effector in the ZYZ convention, leading to the following parametrisation of the task space:
In (17),
![]() ${\boldsymbol{{R}}}_Z(\alpha ) \in{\mathbb{SO}(3)}$
(i.e., the special orthogonal group of three dimensions) is the rotation matrix corresponding to a CCW rotation about the positive
${\boldsymbol{{R}}}_Z(\alpha ) \in{\mathbb{SO}(3)}$
(i.e., the special orthogonal group of three dimensions) is the rotation matrix corresponding to a CCW rotation about the positive
![]() ${\boldsymbol{{Z}}}$
axis by an angle
${\boldsymbol{{Z}}}$
axis by an angle
![]() $\alpha$
, and so on. For the sake of convenience, the following variables are introduced, which are combinations of previously defined joint angles, Euler angles and architecture parameters:
$\alpha$
, and so on. For the sake of convenience, the following variables are introduced, which are combinations of previously defined joint angles, Euler angles and architecture parameters:
The poses of the end-effector expressed through the left and the right chains, that is, using (1) and (2), are used for solving the IKP. The pose of the end-effector can be described using (4). Rewriting (4) using (1), that is, the pose of the end-effector considering the left chain, leads to:
The three components of the displacement vectors on both sides of (18) are equated to obtain:
Additionally, equating the elements (1,3), (3,2) and (3,3) of the rotation matrices on both sides of (18) leads to the following equations:
Equations (19)–(24) are functions of the seven unknown variables appearing in the left chain, that is,
![]() ${\boldsymbol{{q}}}_L = [\theta _{\alpha _1}, \theta _{2L}, \theta _{23L}, \phi _{4L}, \phi _{5L}, \psi _{6L}, \theta _{\gamma _7}]^\top$
.
${\boldsymbol{{q}}}_L = [\theta _{\alpha _1}, \theta _{2L}, \theta _{23L}, \phi _{4L}, \phi _{5L}, \psi _{6L}, \theta _{\gamma _7}]^\top$
.
Similarly, rewriting (4) using (2), that is, the pose of the end-effector expressed through the right chain, yields
Equating the three elements of the displacement vector on both sides of (25) produces
Moreover, the elements (1,3), (2,3) and (3,2) of the rotation matrices on both sides of (25) are equated to obtain:
 \begin{align}{\zeta _{1R}}&\,{:\!=}\, \sin \theta _{23R}-\sin \theta _{\alpha _1}(\!\cos \phi _{5R} \sin \theta _{\gamma _7} \sin \kappa +\sin \phi _{5R} (\!\cos \kappa \cos \phi _{6R} \sin \theta _{\gamma _7}\nonumber\\ &\quad +\cos \theta _{\gamma _7} \sin \phi _{6R})) +\cos \theta _{\alpha _1}(\!\cos \beta (\!\sin \kappa \cos \phi _{5R} \cos \theta _{\gamma _7} -\sin \phi _{5R}(\!\sin \phi _{6R} \sin \theta _{\gamma _7} \nonumber\\ &\quad -\cos \kappa \cos \phi _{6R} \cos \theta _{\gamma _7})) -\sin \beta (\!\sin \kappa \sin \phi _{5R} \cos \phi _{6R}-\cos \kappa \cos \phi _{5R})) =0, \end{align}
\begin{align}{\zeta _{1R}}&\,{:\!=}\, \sin \theta _{23R}-\sin \theta _{\alpha _1}(\!\cos \phi _{5R} \sin \theta _{\gamma _7} \sin \kappa +\sin \phi _{5R} (\!\cos \kappa \cos \phi _{6R} \sin \theta _{\gamma _7}\nonumber\\ &\quad +\cos \theta _{\gamma _7} \sin \phi _{6R})) +\cos \theta _{\alpha _1}(\!\cos \beta (\!\sin \kappa \cos \phi _{5R} \cos \theta _{\gamma _7} -\sin \phi _{5R}(\!\sin \phi _{6R} \sin \theta _{\gamma _7} \nonumber\\ &\quad -\cos \kappa \cos \phi _{6R} \cos \theta _{\gamma _7})) -\sin \beta (\!\sin \kappa \sin \phi _{5R} \cos \phi _{6R}-\cos \kappa \cos \phi _{5R})) =0, \end{align}
 \begin{align} \zeta _{2R} &\,{:\!=}\, \cos \theta _{\alpha _1}(\!\sin \phi _{5R}(\!\cos \kappa \cos \phi _{6R} \sin \theta _{\gamma _7}+\cos \theta _{\gamma _7} \sin \phi _{6R})+\cos \phi _{5R}\sin \theta _{\gamma _7} \sin \kappa ) \nonumber\\ &\quad + \cos \beta \sin \theta _{\alpha _1} (\!\sin \phi _{5R}(\!\cos \kappa \cos \phi _{6R} \cos \theta _{\gamma _7}-\sin \theta _{\gamma _7} \sin \phi _{6R}))\nonumber\\ &\quad + \sin \beta \sin \theta _{\alpha _1} (\!\cos \kappa \cos \phi _{5R} -\sin \kappa \sin \phi _{5R} \cos \phi _{6R})=0, \end{align}
\begin{align} \zeta _{2R} &\,{:\!=}\, \cos \theta _{\alpha _1}(\!\sin \phi _{5R}(\!\cos \kappa \cos \phi _{6R} \sin \theta _{\gamma _7}+\cos \theta _{\gamma _7} \sin \phi _{6R})+\cos \phi _{5R}\sin \theta _{\gamma _7} \sin \kappa ) \nonumber\\ &\quad + \cos \beta \sin \theta _{\alpha _1} (\!\sin \phi _{5R}(\!\cos \kappa \cos \phi _{6R} \cos \theta _{\gamma _7}-\sin \theta _{\gamma _7} \sin \phi _{6R}))\nonumber\\ &\quad + \sin \beta \sin \theta _{\alpha _1} (\!\cos \kappa \cos \phi _{5R} -\sin \kappa \sin \phi _{5R} \cos \phi _{6R})=0, \end{align}
 \begin{align}{\zeta _{3R}}&\,{:\!=}\, \sin \phi _{4R}(\!\cos \beta \sin \kappa \sin \phi _{6R} + \sin \beta (\!\sin \theta _{\gamma _7} \cos \phi _{6R} + \cos \theta _{\gamma _7} \sin \phi _{6R} \cos \kappa ))\nonumber\\ &\quad +\cos \phi _{4R}(\!\sin \beta (\!\cos \theta _{\gamma _7} \sin \kappa \sin \phi _{5R} - \cos \phi _{5R} (\!\cos \theta _{\gamma _7} \cos \kappa \cos \phi _{6R} \nonumber\\ &\quad -\sin \theta _{\gamma _7} \sin \phi _{6R})) -\cos \beta (\!\cos \phi _{5R} \cos \phi _{6R} \sin \kappa + \cos \kappa \sin \phi _{5R}))=0. \end{align}
\begin{align}{\zeta _{3R}}&\,{:\!=}\, \sin \phi _{4R}(\!\cos \beta \sin \kappa \sin \phi _{6R} + \sin \beta (\!\sin \theta _{\gamma _7} \cos \phi _{6R} + \cos \theta _{\gamma _7} \sin \phi _{6R} \cos \kappa ))\nonumber\\ &\quad +\cos \phi _{4R}(\!\sin \beta (\!\cos \theta _{\gamma _7} \sin \kappa \sin \phi _{5R} - \cos \phi _{5R} (\!\cos \theta _{\gamma _7} \cos \kappa \cos \phi _{6R} \nonumber\\ &\quad -\sin \theta _{\gamma _7} \sin \phi _{6R})) -\cos \beta (\!\cos \phi _{5R} \cos \phi _{6R} \sin \kappa + \cos \kappa \sin \phi _{5R}))=0. \end{align}
It may be observed that Eqs. (26)–(31) are functions of the seven unknown variables appearing in the right chain, that is,
![]() ${\boldsymbol{{q}}}_R=[\theta _{\alpha _1}, \theta _{2R}, \theta _{23R}, \phi _{4R}, \phi _{5R}, \phi _{6R}, \theta _{\gamma _7}]^\top$
. From the elements of displacement vectors and rotation matrices of the left and right chains, that is, Eqs. (19)–(24) and Eqs. (26)–(31), equations with the least number of unknown variables appearing in them are chosen to construct the set of constraint equations defining the IKP. In this process, the IKP is defined in terms of the following constraint equations:
${\boldsymbol{{q}}}_R=[\theta _{\alpha _1}, \theta _{2R}, \theta _{23R}, \phi _{4R}, \phi _{5R}, \phi _{6R}, \theta _{\gamma _7}]^\top$
. From the elements of displacement vectors and rotation matrices of the left and right chains, that is, Eqs. (19)–(24) and Eqs. (26)–(31), equations with the least number of unknown variables appearing in them are chosen to construct the set of constraint equations defining the IKP. In this process, the IKP is defined in terms of the following constraint equations:
![]() $\boldsymbol{\eta }_{IK}=\{\eta _1, \eta _2, \eta _3, \eta _4, \eta _5, \eta _6\}=\textbf{0}$
. In the aforementioned equations,
$\boldsymbol{\eta }_{IK}=\{\eta _1, \eta _2, \eta _3, \eta _4, \eta _5, \eta _6\}=\textbf{0}$
. In the aforementioned equations,
![]() $\{\eta _1, \eta _2, \eta _3, \eta _4, \eta _5, \eta _6\} = \{\eta _{1L}, \eta _{2L}, \eta _{3L}, \zeta _{1L}, \zeta _{2L}, \eta _{2R}\}$
(see Eqs. (19)–(23) and (27)) are functions of the unknown variables
$\{\eta _1, \eta _2, \eta _3, \eta _4, \eta _5, \eta _6\} = \{\eta _{1L}, \eta _{2L}, \eta _{3L}, \zeta _{1L}, \zeta _{2L}, \eta _{2R}\}$
(see Eqs. (19)–(23) and (27)) are functions of the unknown variables
![]() ${\boldsymbol{{q}}}=[\theta _{\alpha _1}, \theta _{2L}, \theta _{23L}, \phi _{5L}, \psi _{6L}, \theta _{\gamma _7}]^\top$
:
${\boldsymbol{{q}}}=[\theta _{\alpha _1}, \theta _{2L}, \theta _{23L}, \phi _{5L}, \psi _{6L}, \theta _{\gamma _7}]^\top$
:
In Eqs. (32)–(37), only the unknown variables are shown explicitly. The remaining six equations, that is, Eqs. (24), (26) and (28)–(31), are used later to solve for the remaining variables
![]() $\{\phi _{4L}, \theta _{2R}, \theta _{23R}$
,
$\{\phi _{4L}, \theta _{2R}, \theta _{23R}$
,
![]() $\phi _{4R}, \phi _{5R}, \phi _{6R}\}$
. The order of elimination of variables is chosen based on the number of appearances, starting with the smallest one. In other words, the variable appearing in the lowest number of equations at each step is eliminated thereafter. This results in the following sequence of variables to be eliminated:
$\phi _{4R}, \phi _{5R}, \phi _{6R}\}$
. The order of elimination of variables is chosen based on the number of appearances, starting with the smallest one. In other words, the variable appearing in the lowest number of equations at each step is eliminated thereafter. This results in the following sequence of variables to be eliminated:
![]() $ \theta _{2L}, \phi _{5L}, \theta _{23L}, \psi _{6L}, \theta _{\gamma _7}$
. The details of these eliminations are presented in the following.
$ \theta _{2L}, \phi _{5L}, \theta _{23L}, \psi _{6L}, \theta _{\gamma _7}$
. The details of these eliminations are presented in the following.
4.1. Elimination of
 $\theta _{2L}$
$\theta _{2L}$
The constraint equations
![]() $\eta _1 = 0$
(see (19)) and
$\eta _1 = 0$
(see (19)) and
![]() $\eta _3 = 0$
(see (21)) are linear in the sine and cosine of
$\eta _3 = 0$
(see (21)) are linear in the sine and cosine of
![]() $\theta _{2L}$
, respectively. Hence, the expressions of
$\theta _{2L}$
, respectively. Hence, the expressions of
![]() $\sin \theta _{2L}$
and
$\sin \theta _{2L}$
and
![]() $\cos \theta _{2L}$
are obtained from Eqs. (19) and (21):
$\cos \theta _{2L}$
are obtained from Eqs. (19) and (21):
In (38), the polynomials
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\lambda _2$
are functions of the variables
$\lambda _2$
are functions of the variables
![]() $\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}$
and
$\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}$
and
![]() $\theta _{23L}$
. Substituting the expressions of
$\theta _{23L}$
. Substituting the expressions of
![]() $\sin \theta _{2L}$
and
$\sin \theta _{2L}$
and
![]() $\cos \theta _{2L}$
in the trigonometric identity
$\cos \theta _{2L}$
in the trigonometric identity
![]() $\cos ^2\theta _{2L} + \sin ^2\theta _{2L} = 1$
leads to a new equation in the remaining variables, namely
$\cos ^2\theta _{2L} + \sin ^2\theta _{2L} = 1$
leads to a new equation in the remaining variables, namely
![]() $f(\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{23L})= 0$
. The resulting elimination of
$f(\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{23L})= 0$
. The resulting elimination of
![]() $\theta _{2L}$
is depicted below schematically:Footnote
10
$\theta _{2L}$
is depicted below schematically:Footnote
10
 \begin{align} &\begin{array}{cc}\left. \begin{array}{ll}{\eta _1(\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{2L}, \theta _{23L}) = 0}\\[4pt] \eta _3(\theta _{\gamma _7}, \psi _{6L}, \theta _{2L}, \theta _{23L}) = 0\\ \end{array} \right ){\xrightarrow{\times \theta _{2L}}} \end{array} \begin{array}{cc} f(\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{23L})= 0. \end{array} \end{align}
\begin{align} &\begin{array}{cc}\left. \begin{array}{ll}{\eta _1(\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{2L}, \theta _{23L}) = 0}\\[4pt] \eta _3(\theta _{\gamma _7}, \psi _{6L}, \theta _{2L}, \theta _{23L}) = 0\\ \end{array} \right ){\xrightarrow{\times \theta _{2L}}} \end{array} \begin{array}{cc} f(\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{23L})= 0. \end{array} \end{align}
4.2. Elimination of
 $\phi _{5L}$
$\phi _{5L}$
Equations
![]() $\eta _4=0$
and
$\eta _4=0$
and
![]() $\eta _5=0$
(see Eqs. (22) and (23)) are linear in the sine and cosine of
$\eta _5=0$
(see Eqs. (22) and (23)) are linear in the sine and cosine of
![]() $(\phi _{5L}+\psi _{6L})$
and hence may be represented as:
$(\phi _{5L}+\psi _{6L})$
and hence may be represented as:
where the coefficients
![]() $i_i, j_i$
and
$i_i, j_i$
and
![]() $k_i$
are functions of the variables
$k_i$
are functions of the variables
![]() $\theta _{23L}, \psi _{6L}$
and
$\theta _{23L}, \psi _{6L}$
and
![]() $\theta _{\gamma _7}$
. The expressions of
$\theta _{\gamma _7}$
. The expressions of
![]() $\sin (\phi _{5L}+\psi _{6L})$
and
$\sin (\phi _{5L}+\psi _{6L})$
and
![]() $\cos (\phi _{5L}+\psi _{6L})$
are obtained from these equations and substituted in the trigonometric identity
$\cos (\phi _{5L}+\psi _{6L})$
are obtained from these equations and substituted in the trigonometric identity
![]() $\cos ^2(\phi _{5L}+\psi _{6L})+\sin ^2(\phi _{5L}+\psi _{6L})=1$
yielding:
$\cos ^2(\phi _{5L}+\psi _{6L})+\sin ^2(\phi _{5L}+\psi _{6L})=1$
yielding:
The above equation is obtained assumingFootnote 11 that:
Equation (42) represents a kinematic constraint in the unknown variables
![]() $\theta _{\alpha _1}, \theta _{\gamma _7},$
and
$\theta _{\alpha _1}, \theta _{\gamma _7},$
and
![]() $\theta _{23L}$
. Furthermore, the conditions
$\theta _{23L}$
. Furthermore, the conditions
![]() $i_1^2+j_1^2-k_1^2=0$
and
$i_1^2+j_1^2-k_1^2=0$
and
![]() $i_2^2+j_2^2-k_2^2=0$
cause repeated roots to satisfy (40) and (41), respectively. The details of this singularity are discussed in Case 1 in Section 6.2.
$i_2^2+j_2^2-k_2^2=0$
cause repeated roots to satisfy (40) and (41), respectively. The details of this singularity are discussed in Case 1 in Section 6.2.
4.3. Elimination of
 $\theta _{23L}$
$\theta _{23L}$
The constraint equations
![]() $n=0$
(see (42)) and
$n=0$
(see (42)) and
![]() $f=0$
(see (39)) are both linear in the sine and cosine of
$f=0$
(see (39)) are both linear in the sine and cosine of
![]() $\theta _{23L}$
and can be written explicitly in terms of
$\theta _{23L}$
and can be written explicitly in terms of
![]() $\cos \theta _{23L}$
and
$\cos \theta _{23L}$
and
![]() $\sin \theta _{23L}$
as:
$\sin \theta _{23L}$
as:
As shown in Eqs. (44) and (45), the coefficients
![]() $a_i$
,
$a_i$
,
![]() $b_i$
and
$b_i$
and
![]() $c_i$
(
$c_i$
(
![]() $i=1,2$
) are functions of the unknown variables
$i=1,2$
) are functions of the unknown variables
![]() $\theta _{\alpha _1}, \psi _{6L}$
and
$\theta _{\alpha _1}, \psi _{6L}$
and
![]() $\theta _{\gamma _7}$
. Subsequently, the variable
$\theta _{\gamma _7}$
. Subsequently, the variable
![]() $\theta _{23L}$
is eliminated following the procedure described in Sections 4.1 and 4.2, leading to the equation:
$\theta _{23L}$
is eliminated following the procedure described in Sections 4.1 and 4.2, leading to the equation:
It is assumed in the above that:
Transferring
![]() $|ab|^2$
to the right-hand side of (46) and taking square roots of both the sides and rearranging, one obtains
$|ab|^2$
to the right-hand side of (46) and taking square roots of both the sides and rearranging, one obtains
The size
Footnote
12
of the symbolic expression of
![]() $h$
is
$h$
is
![]() $13.080$
KB.
$13.080$
KB.
The identification of the form of (46) was made possible solely by the exact symbolic approach adopted in this work. It has allowed the reduction of this equation to (48), a step which is of critical importance in the symbolic computation scheme leading to the final univariate equation. It is a key enabler in permitting the computation to continue in the exact symbolic form, for two reasons: (a) it halves the degrees of the relevant variables appearing in (46) and (b) it helps in reducing the sizes of the expressions involved rather dramatically, without which the subsequent computations would have been rendered impractical (due to the demands on computational resources and time) or even infeasible. Consider, for instance, (53), which is derived below after a few steps. If it were to be derived directly from (46), it would have had a size of
![]() $6.110$
MB, which might have deterred subsequent symbolic computations. Also, the equation
$6.110$
MB, which might have deterred subsequent symbolic computations. Also, the equation
![]() $p = 0$
would have been a quartic in the variable
$p = 0$
would have been a quartic in the variable
![]() $c_6$
, making its elimination significantly more difficult in the computations that follow the derivation of (53). However, when the same equation is derived from (48), not only
$c_6$
, making its elimination significantly more difficult in the computations that follow the derivation of (53). However, when the same equation is derived from (48), not only
![]() $p$
becomes a quadratic function of
$p$
becomes a quadratic function of
![]() $c_6$
, as an expression, its size is reduced to only
$c_6$
, as an expression, its size is reduced to only
![]() $19.232$
KB, that is, it is reduced by a factor greater than
$19.232$
KB, that is, it is reduced by a factor greater than
![]() $300$
. As mentioned in Section 7, this and similar custom-developed techniques in symbolic computation allow the derivation of the key results in this paper.
$300$
. As mentioned in Section 7, this and similar custom-developed techniques in symbolic computation allow the derivation of the key results in this paper.
It may be noted from (44) that
![]() $\theta _{23L}$
has finite number of values iff:
$\theta _{23L}$
has finite number of values iff:
The condition
![]() $|ab|=0$
(see (47)), also causedFootnote
13
by
$|ab|=0$
(see (47)), also causedFootnote
13
by
![]() $\mu =0$
(see (48)), results in a singularity of the manipulator. The details of the singularity are discussed in Case 2 in Section 6.2. Further, the condition
$\mu =0$
(see (48)), results in a singularity of the manipulator. The details of the singularity are discussed in Case 2 in Section 6.2. Further, the condition
![]() $a_2^2+b_2^2-c_2^2=0$
leads to a double root of (45). The corresponding singularity is also studied in Section 6.2, in Case 3. It is worth mentioning that a merger of the solutions of the variable
$a_2^2+b_2^2-c_2^2=0$
leads to a double root of (45). The corresponding singularity is also studied in Section 6.2, in Case 3. It is worth mentioning that a merger of the solutions of the variable
![]() $\theta _{23L}$
leads to a repeated solution of the variable
$\theta _{23L}$
leads to a repeated solution of the variable
![]() $\theta _{2L}$
as well.
$\theta _{2L}$
as well.
4.4. Elimination of
 $\psi _{6L}$
$\psi _{6L}$
The constraint equation
![]() $\eta _2=0$
(see (20)) is linear in the cosine and sine of
$\eta _2=0$
(see (20)) is linear in the cosine and sine of
![]() $\psi _{6L}$
or, equivalently, linear in {
$\psi _{6L}$
or, equivalently, linear in {
![]() $c_6$
,
$c_6$
,
![]() $s_6$
}, where
$s_6$
}, where
![]() $c_6=(a_6-l_w \cos \psi _{6L})$
and
$c_6=(a_6-l_w \cos \psi _{6L})$
and
![]() $s_6=(d_7 - l_w \sin \psi _{6L})$
. Therefore, for the sake of convenience,
$s_6=(d_7 - l_w \sin \psi _{6L})$
. Therefore, for the sake of convenience,
![]() $\eta _2 = 0$
(see (20)) and
$\eta _2 = 0$
(see (20)) and
![]() $h=0$
(see (48)) are written in terms of {
$h=0$
(see (48)) are written in terms of {
![]() $c_6$
,
$c_6$
,
![]() $s_6$
} leading to the equations
$s_6$
} leading to the equations
![]() $g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right)=0$
and
$g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right)=0$
and
![]() $g_2\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right)=0$
, respectively:
$g_2\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right)=0$
, respectively:
 \begin{align} &\begin{array}{cc} \begin{array}{ll} \begin{aligned} &\eta _2\left(\theta _{\gamma _7}, \theta _{\alpha _1}, \psi _{6L}\right) = 0{\xrightarrow{\psi _{6L} \rightarrow c_6, s_6}} && g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0,\\ &h\left(\theta _{\gamma _7}, \theta _{\alpha _1}, \psi _{6L}\right) = 0{\xrightarrow{\psi _{6L} \rightarrow c_6, s_6}} && g_2\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0.\\ \end{aligned} \end{array} \end{array} \end{align}
\begin{align} &\begin{array}{cc} \begin{array}{ll} \begin{aligned} &\eta _2\left(\theta _{\gamma _7}, \theta _{\alpha _1}, \psi _{6L}\right) = 0{\xrightarrow{\psi _{6L} \rightarrow c_6, s_6}} && g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0,\\ &h\left(\theta _{\gamma _7}, \theta _{\alpha _1}, \psi _{6L}\right) = 0{\xrightarrow{\psi _{6L} \rightarrow c_6, s_6}} && g_2\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0.\\ \end{aligned} \end{array} \end{array} \end{align}
In the above, the symbol ‘
![]() $\xrightarrow{\psi _{6L} \rightarrow c_6, s_6}$
’ implies the absorption of the trigonometric variables of
$\xrightarrow{\psi _{6L} \rightarrow c_6, s_6}$
’ implies the absorption of the trigonometric variables of
![]() $\psi _{6L}$
into the algebraic variables
$\psi _{6L}$
into the algebraic variables
![]() $s_6$
and
$s_6$
and
![]() $c_6$
. Subsequently, the expression of
$c_6$
. Subsequently, the expression of
![]() $s_6$
is obtained in terms of
$s_6$
is obtained in terms of
![]() $c_6$
from
$c_6$
from
![]() $g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0$
:Footnote
14
$g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0$
:Footnote
14
Substituting
![]() $s_6$
from (51) in the modified trigonometric identity
$s_6$
from (51) in the modified trigonometric identity
![]() $(a_6-c_6)^2+(d_7-s_6)^2=l_w^2$
yields a quadratic equation in
$(a_6-c_6)^2+(d_7-s_6)^2=l_w^2$
yields a quadratic equation in
![]() $c_6$
, denoted by
$c_6$
, denoted by
![]() $g\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right)=0$
:
$g\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right)=0$
:
 \begin{align} &\begin{array}{cc}\left. \begin{array}{ll} g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0\\ \\[-8pt] (a_6 - c_6)^2+(d_7 - s_6)^2-l_w^2=0 \\ \end{array} \right ){\xrightarrow{\times s_6}} \end{array} \begin{array}{cc} g\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right)=0. \end{array} \end{align}
\begin{align} &\begin{array}{cc}\left. \begin{array}{ll} g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0\\ \\[-8pt] (a_6 - c_6)^2+(d_7 - s_6)^2-l_w^2=0 \\ \end{array} \right ){\xrightarrow{\times s_6}} \end{array} \begin{array}{cc} g\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right)=0. \end{array} \end{align}
Likewise, the expression of
![]() $s_6$
presented in (51) is substituted in
$s_6$
presented in (51) is substituted in
![]() $g_2=0$
(see (50)) to obtain a quadratic in
$g_2=0$
(see (50)) to obtain a quadratic in
![]() $c_6$
of size
$c_6$
of size
![]() $19.232$
KB, namely
$19.232$
KB, namely
![]() $p\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right)=0$
:
$p\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right)=0$
:
 \begin{align} &\begin{array}{cc}\left. \begin{array}{ll} \begin{aligned} & g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0\\ \\[-8pt] & g_2\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0\\ \end{aligned} \end{array} \right ){\xrightarrow{\times s_6}} \end{array} \begin{array}{cc} \begin{aligned} p\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right)=0. \end{aligned} \end{array} \end{align}
\begin{align} &\begin{array}{cc}\left. \begin{array}{ll} \begin{aligned} & g_1\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0\\ \\[-8pt] & g_2\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6, s_6\right) = 0\\ \end{aligned} \end{array} \right ){\xrightarrow{\times s_6}} \end{array} \begin{array}{cc} \begin{aligned} p\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right)=0. \end{aligned} \end{array} \end{align}
Hereafter, the equations
![]() $g=0$
and
$g=0$
and
![]() $p=0$
may be represented as:
$p=0$
may be represented as:
where the coefficients
![]() $a_i, b_i$
and
$a_i, b_i$
and
![]() $c_i$
(
$c_i$
(
![]() $i=3,4$
) are functions of the variables
$i=3,4$
) are functions of the variables
![]() $\theta _{\gamma _7}$
and
$\theta _{\gamma _7}$
and
![]() $\theta _{\alpha _1}$
. Simultaneous satisfaction of the conditions
$\theta _{\alpha _1}$
. Simultaneous satisfaction of the conditions
![]() $b_3^2- 4a_3c_3= 0$
and
$b_3^2- 4a_3c_3= 0$
and
![]() $b_4^2-4 a_4 c_4=0$
causes the roots of Eqs. (54) and (55) to repeat. The corresponding singularity is discussed under Case 4 in Section 6.2. The resultantFootnote
15
of
$b_4^2-4 a_4 c_4=0$
causes the roots of Eqs. (54) and (55) to repeat. The corresponding singularity is discussed under Case 4 in Section 6.2. The resultantFootnote
15
of
![]() $p = 0$
and
$p = 0$
and
![]() $g = 0$
with respect to
$g = 0$
with respect to
![]() $c_6$
eliminatesFootnote
16
the variable and leads to a new equation
$c_6$
eliminatesFootnote
16
the variable and leads to a new equation
![]() $q\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)=0$
of size
$q\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)=0$
of size
![]() $839.088$
KB:
$839.088$
KB:
 \begin{align} &\begin{array}{cc}\left. \begin{array}{ll} p\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right) = 0 \\ \\[-8pt] g\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right) = 0 \\ \end{array} \right ){\xrightarrow{\times c_6}} \end{array} \begin{array}{cc} q\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0. \end{array} \end{align}
\begin{align} &\begin{array}{cc}\left. \begin{array}{ll} p\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right) = 0 \\ \\[-8pt] g\left(\theta _{\gamma _7}, \theta _{\alpha _1}, c_6\right) = 0 \\ \end{array} \right ){\xrightarrow{\times c_6}} \end{array} \begin{array}{cc} q\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0. \end{array} \end{align}
As noted before, the elimination of
![]() $c_6$
was greatly facilitated by the reduction of (46) to (48).
$c_6$
was greatly facilitated by the reduction of (46) to (48).
Continuing further, the function
![]() $q=0$
was simplified symbolically,Footnote
17
which afforded its factorisation in the following manner:
$q=0$
was simplified symbolically,Footnote
17
which afforded its factorisation in the following manner:
where
![]() $\delta \left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)$
is a cubic polynomial in
$\delta \left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)$
is a cubic polynomial in
![]() $\mu$
. Since it has already been assumed that
$\mu$
. Since it has already been assumed that
![]() $\mu \neq 0$
and
$\mu \neq 0$
and
![]() $\sin \beta \sin \theta _{\alpha _1}\neq 0$
(in the context of Eqs. (49) and (51)), (57) reduces to
$\sin \beta \sin \theta _{\alpha _1}\neq 0$
(in the context of Eqs. (49) and (51)), (57) reduces to
![]() $\delta \left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)=0$
, which may be written as:
$\delta \left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)=0$
, which may be written as:
The coefficients in (58), namely
![]() $m_i$
, are also functions of the variables
$m_i$
, are also functions of the variables
![]() $\theta _{\gamma _7}$
and
$\theta _{\gamma _7}$
and
![]() $\theta _{\alpha _1}$
. Since it is known (from (48)) that
$\theta _{\alpha _1}$
. Since it is known (from (48)) that
![]() $\mu ^2 = a_1^2 + b_1^2$
, (58) is manipulated to derive its equivalent, cast in terms of
$\mu ^2 = a_1^2 + b_1^2$
, (58) is manipulated to derive its equivalent, cast in terms of
![]() $\mu ^2$
:
$\mu ^2$
:
Direct substitution of the expressions of the coefficients
![]() $m_i$
and
$m_i$
and
![]() $\mu ^2$
in (59) leads to the following equation free of radicals:
$\mu ^2$
in (59) leads to the following equation free of radicals:
 \begin{align} &\begin{array}{cc}\left. \begin{array}{ll} \delta _1\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0\\ \\[-8pt] \mu ^2 - \left(a_1^2 + b_1^2\right) = 0 \\ \end{array} \right ){\xrightarrow{\times \mu ^2}} \end{array} \begin{array}{cc} r\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0. \end{array} \end{align}
\begin{align} &\begin{array}{cc}\left. \begin{array}{ll} \delta _1\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0\\ \\[-8pt] \mu ^2 - \left(a_1^2 + b_1^2\right) = 0 \\ \end{array} \right ){\xrightarrow{\times \mu ^2}} \end{array} \begin{array}{cc} r\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0. \end{array} \end{align}
However, the size of
![]() $r\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)$
, even after rigorous simplification, stands at
$r\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)$
, even after rigorous simplification, stands at
![]() $216.140$
MB. It is reduced in the next step, before proceeding further.
$216.140$
MB. It is reduced in the next step, before proceeding further.
4.5. Elimination of
 $\theta _{\gamma _7}$
$\theta _{\gamma _7}$
The expression
![]() $r\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)$
turns out to be cubic in
$r\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right)$
turns out to be cubic in
![]() $\cos \theta _{\gamma _7}$
. However, using the identities:
$\cos \theta _{\gamma _7}$
. However, using the identities:
(60) is reduced to:
The polynomial
![]() $r_l$
is linear in
$r_l$
is linear in
![]() $\cos \theta _{\gamma _7}$
. Furthermore, this reduction results in fewer coefficients, which, upon symbolic simplification, shrink to the size of
$\cos \theta _{\gamma _7}$
. Furthermore, this reduction results in fewer coefficients, which, upon symbolic simplification, shrink to the size of
![]() $89.311$
MB. It may be noted here that the equation
$89.311$
MB. It may be noted here that the equation
![]() $\eta _6=0$
(see (27)), is also linear in
$\eta _6=0$
(see (27)), is also linear in
![]() $\cos \theta _{\gamma _7}$
and
$\cos \theta _{\gamma _7}$
and
![]() $\sin \theta _{\gamma _7}$
, from which one can find
$\sin \theta _{\gamma _7}$
, from which one can find
![]() $cos\theta _{\gamma _7}$
in terms of
$cos\theta _{\gamma _7}$
in terms of
![]() $\sin \theta _{\gamma _7}$
:Footnote
18
$\sin \theta _{\gamma _7}$
:Footnote
18
In (63),
![]() $\nu \left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right)$
is linear in
$\nu \left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right)$
is linear in
![]() $\cos \theta _{\alpha _1}$
,
$\cos \theta _{\alpha _1}$
,
![]() $\sin \theta _{\alpha _1}$
and
$\sin \theta _{\alpha _1}$
and
![]() $\sin \theta _{\gamma _7}$
. Substituting the expression of
$\sin \theta _{\gamma _7}$
. Substituting the expression of
![]() $\cos \theta _{\gamma _7}$
in (62) results in a sextic equation in
$\cos \theta _{\gamma _7}$
in (62) results in a sextic equation in
![]() $\sin \theta _{\gamma _7}$
, namely
$\sin \theta _{\gamma _7}$
, namely
![]() $u_1\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right)=0$
:
$u_1\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right)=0$
:
 \begin{align} &\begin{array}{cc}\left. \begin{array}{ll} \eta _6\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0 \\ \\[-9pt] r_l\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0 \\ \end{array} \right ){\xrightarrow{\times \cos \theta _{\gamma _7}}} \end{array} \begin{array}{cc} u_1\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0. \end{array} \end{align}
\begin{align} &\begin{array}{cc}\left. \begin{array}{ll} \eta _6\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0 \\ \\[-9pt] r_l\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0 \\ \end{array} \right ){\xrightarrow{\times \cos \theta _{\gamma _7}}} \end{array} \begin{array}{cc} u_1\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0. \end{array} \end{align}
It may be noted here that the reduction of (60) to (62) is yet another improvisation in symbolic computation which has played a crucial role in the derivation of the inverse kinematic univariate (IKU) in its symbolic form. Specifically, if the equation
![]() $r = 0$
was used in (64) instead of
$r = 0$
was used in (64) instead of
![]() $r_l= 0$
, the resulting size of
$r_l= 0$
, the resulting size of
![]() $u_1$
would have been
$u_1$
would have been
![]() $191.635$
MB. However, due to the said reduction, the actual size turns out to be
$191.635$
MB. However, due to the said reduction, the actual size turns out to be
![]() $79.873$
MB, which allows the computation to proceed further.
$79.873$
MB, which allows the computation to proceed further.
In the next step, the expression of
![]() $\cos \theta _{\gamma _7}$
(from (63)) is substituted in the trigonometric identity
$\cos \theta _{\gamma _7}$
(from (63)) is substituted in the trigonometric identity
![]() $\cos ^2\theta _{\gamma _7}+ \sin ^2\theta _{\gamma _7} = 1$
, to obtain a quadratic equation in
$\cos ^2\theta _{\gamma _7}+ \sin ^2\theta _{\gamma _7} = 1$
, to obtain a quadratic equation in
![]() $\sin \theta _{\gamma _7}$
, namely
$\sin \theta _{\gamma _7}$
, namely
![]() $u_2\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0$
:
$u_2\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0$
:
 \begin{align} &\begin{array}{cc}\left. \begin{array}{ll} \eta _6\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0 \\ \\[-6pt] \cos ^2\theta _{\gamma _7}+\sin ^2\theta _{\gamma _7} - 1 = 0 \\ \end{array} \right ){\xrightarrow{\times \cos \theta _{\gamma _7}}} \end{array} \begin{array}{cc} u_2\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0. \end{array} \end{align}
\begin{align} &\begin{array}{cc}\left. \begin{array}{ll} \eta _6\left(\theta _{\gamma _7}, \theta _{\alpha _1}\right) = 0 \\ \\[-6pt] \cos ^2\theta _{\gamma _7}+\sin ^2\theta _{\gamma _7} - 1 = 0 \\ \end{array} \right ){\xrightarrow{\times \cos \theta _{\gamma _7}}} \end{array} \begin{array}{cc} u_2\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0. \end{array} \end{align}
Eliminating
![]() $\sin \theta _{\gamma _7}$
between Eqs. (64) and (65) yields the univariate equation in
$\sin \theta _{\gamma _7}$
between Eqs. (64) and (65) yields the univariate equation in
![]() $\theta _{\alpha _1}$
, that is,
$\theta _{\alpha _1}$
, that is,
![]() $u(\theta _{\alpha _1})= 0$
, which is of total degree
$u(\theta _{\alpha _1})= 0$
, which is of total degree
![]() $26$
in
$26$
in
![]() $\sin \theta _{\alpha _1}$
and
$\sin \theta _{\alpha _1}$
and
![]() $\cos \theta _{\alpha _1}$
:
$\cos \theta _{\alpha _1}$
:
 \begin{align} &\begin{array}{cc}\left. \begin{array}{ll} u_1\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0 \\ \\[-6pt] u_2\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0 \\ \end{array} \right ){\xrightarrow{\times \sin \theta _{\gamma _7}}} \end{array} \begin{array}{cc} u(\theta _{\alpha _1}) = 0. \end{array} \end{align}
\begin{align} &\begin{array}{cc}\left. \begin{array}{ll} u_1\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0 \\ \\[-6pt] u_2\left(\theta _{\alpha _1}, \sin \theta _{\gamma _7}\right) = 0 \\ \end{array} \right ){\xrightarrow{\times \sin \theta _{\gamma _7}}} \end{array} \begin{array}{cc} u(\theta _{\alpha _1}) = 0. \end{array} \end{align}
Therefore, one may arrive at the final univariate polynomial from (66), as described in the next subsection. However, before that, a few special cases must be considered, for the sake of completeness.
It may be noted that repeated roots in the sextic equation
![]() $u_1=0$
(see (64)) and the quadratic equation
$u_1=0$
(see (64)) and the quadratic equation
![]() $u_2=0$
(see (65)) cause the manipulator to encounter a singularity. The sextic
$u_2=0$
(see (65)) cause the manipulator to encounter a singularity. The sextic
![]() $u_1= 0$
(see (64)) is a polynomial equation in
$u_1= 0$
(see (64)) is a polynomial equation in
![]() $s_7 = \sin \theta _{\gamma _7}$
and its discriminant may be obtained as:
$s_7 = \sin \theta _{\gamma _7}$
and its discriminant may be obtained as:
In (67),
![]() $\operatorname{res}(a(x),b(x),x)$
denotes the resultant of the polynomials
$\operatorname{res}(a(x),b(x),x)$
denotes the resultant of the polynomials
![]() $a(x)$
and
$a(x)$
and
![]() $b(x)$
w.r.t.
$b(x)$
w.r.t.
![]() $x$
. Further, Equation (65) may be written as:
$x$
. Further, Equation (65) may be written as:
In (68), the coefficients
![]() $a_5, b_5$
and
$a_5, b_5$
and
![]() $c_5$
are functions of
$c_5$
are functions of
![]() $\theta _{\alpha _1}$
alone. Hence, the manipulator encounters a singularity when the discriminants of Eqs. (64) and (65), that is,
$\theta _{\alpha _1}$
alone. Hence, the manipulator encounters a singularity when the discriminants of Eqs. (64) and (65), that is,
![]() $\Delta _{1}$
(see (67)) and
$\Delta _{1}$
(see (67)) and
![]() $b_5^2- 4a_5c_5$
(see (68)), respectively, vanish simultaneously. The corresponding singularity is studied as Case 5 in Section 6.2.
$b_5^2- 4a_5c_5$
(see (68)), respectively, vanish simultaneously. The corresponding singularity is studied as Case 5 in Section 6.2.
4.6. Derivation of the IKU equation
In the following, the total degree of the equation
![]() $u=0$
(66) in
$u=0$
(66) in
![]() $\sin \theta _{\alpha _1}$
and
$\sin \theta _{\alpha _1}$
and
![]() $\cos \theta _{\alpha _1}$
is brought down from
$\cos \theta _{\alpha _1}$
is brought down from
![]() $26$
to
$26$
to
![]() $20$
through the identification and subsequent rejection of spurious factors, which are associated with singular solutions. Once again, this is an important step involving symbolic simplification and factorisation, without which the final univariate polynomial equation, that is, the IKU, would have been of degree 52, and not 40, as it is in (74).
$20$
through the identification and subsequent rejection of spurious factors, which are associated with singular solutions. Once again, this is an important step involving symbolic simplification and factorisation, without which the final univariate polynomial equation, that is, the IKU, would have been of degree 52, and not 40, as it is in (74).
The elimination process in (66) is simplified by rewriting
![]() $u_1=0$
and
$u_1=0$
and
![]() $u_2=0$
as polynomial equations in
$u_2=0$
as polynomial equations in
![]() $\sin \theta _{\gamma _7}$
:
$\sin \theta _{\gamma _7}$
:
 \begin{align} u_1 &\,{:\!=}\, \;\tau (\theta _{\alpha _1}) u_{16} \sin ^6\theta _{\gamma _7} + u_{15} \sin ^5\theta _{\gamma _7} + u_{14} \sin ^4\theta _{\gamma _7} + u_{13} \sin ^3\theta _{\gamma _7\nonumber }\\[3pt] &\quad + u_{12} \sin ^2\theta _{\gamma _7} + u_{11} \sin \theta _{\gamma _7} + u_{10} = 0, \end{align}
\begin{align} u_1 &\,{:\!=}\, \;\tau (\theta _{\alpha _1}) u_{16} \sin ^6\theta _{\gamma _7} + u_{15} \sin ^5\theta _{\gamma _7} + u_{14} \sin ^4\theta _{\gamma _7} + u_{13} \sin ^3\theta _{\gamma _7\nonumber }\\[3pt] &\quad + u_{12} \sin ^2\theta _{\gamma _7} + u_{11} \sin \theta _{\gamma _7} + u_{10} = 0, \end{align}
In the preceding equations, the coefficients
![]() $u_{ij}$
are functions of
$u_{ij}$
are functions of
![]() $\theta _{\alpha _1}$
; also,
$\theta _{\alpha _1}$
; also,
Thus, the resulting equation
![]() $u(\theta _{\alpha _1}) = 0$
obtained by the elimination of
$u(\theta _{\alpha _1}) = 0$
obtained by the elimination of
![]() $\sin \theta _{\gamma _7}$
from Eqs. (69) and (70) depends on
$\sin \theta _{\gamma _7}$
from Eqs. (69) and (70) depends on
![]() $u_{ij}(\theta _{\alpha _1})$
and
$u_{ij}(\theta _{\alpha _1})$
and
![]() $\tau (\theta _{\alpha _1})$
, that is, ultimately, on
$\tau (\theta _{\alpha _1})$
, that is, ultimately, on
![]() $\theta _{\alpha _1}$
alone. It is interesting to note that
$\theta _{\alpha _1}$
alone. It is interesting to note that
![]() $\tau (\theta _{\alpha _1})=0$
trivially satisfies (70) and therefore,
$\tau (\theta _{\alpha _1})=0$
trivially satisfies (70) and therefore,
![]() $\tau (\theta _{\alpha _1})\neq 0$
for
$\tau (\theta _{\alpha _1})\neq 0$
for
![]() $\theta _{\gamma _7}$
to have finite number of values. Expressing
$\theta _{\gamma _7}$
to have finite number of values. Expressing
![]() $u(\theta _{\alpha _1}) = 0$
in terms of the coefficients
$u(\theta _{\alpha _1}) = 0$
in terms of the coefficients
![]() $u_{ij}$
affords the advantage of yielding the factor
$u_{ij}$
affords the advantage of yielding the factor
![]() $\tau ^2(\theta _{\alpha _1})$
without having to handle the large-sized expressions of
$\tau ^2(\theta _{\alpha _1})$
without having to handle the large-sized expressions of
![]() $u_{ij}$
:
$u_{ij}$
:
where
![]() $w_1(\theta _{\alpha _1})$
is a function of
$w_1(\theta _{\alpha _1})$
is a function of
![]() $u_{ij}$
. As the factor
$u_{ij}$
. As the factor
![]() $\tau (\theta _{\alpha _1})$
appears in the leading coefficients of Eqs. (69) and (70), the manipulator encounters a singularity when
$\tau (\theta _{\alpha _1})$
appears in the leading coefficients of Eqs. (69) and (70), the manipulator encounters a singularity when
![]() $\tau (\theta _{\alpha _1})=0$
, which is described in Case 1 of Section 6.2. Therefore, in the non-singular cases, the relevant part of (72) is given by
$\tau (\theta _{\alpha _1})=0$
, which is described in Case 1 of Section 6.2. Therefore, in the non-singular cases, the relevant part of (72) is given by
![]() $w_1(\theta _{\alpha _1})=0$
. Subsequently, the actual expressions of the variables
$w_1(\theta _{\alpha _1})=0$
. Subsequently, the actual expressions of the variables
![]() $u_{ij}$
are substituted in
$u_{ij}$
are substituted in
![]() $w_1=0$
, along with the architecture parameters mentioned in Table III, which increases the size of
$w_1=0$
, along with the architecture parameters mentioned in Table III, which increases the size of
![]() $w_1=0$
significantly to
$w_1=0$
significantly to
![]() $25.388$
MB even before its symbolic expansion, making further computation time-consuming and computationally complex. To overcome the aforementioned issues, the coefficients
$25.388$
MB even before its symbolic expansion, making further computation time-consuming and computationally complex. To overcome the aforementioned issues, the coefficients
![]() $u_{ij}$
are transformed to the respective monomial-based canonical (MBC) forms (see ref. [Reference Bandyopadhyay and Ghosal24], Section 3, for the details), treating
$u_{ij}$
are transformed to the respective monomial-based canonical (MBC) forms (see ref. [Reference Bandyopadhyay and Ghosal24], Section 3, for the details), treating
![]() $\sin \theta _{\gamma _7}$
and
$\sin \theta _{\gamma _7}$
and
![]() $\cos \theta _{\gamma _7}$
as algebraic variables. Consequently, substituting these expressions of the coefficients
$\cos \theta _{\gamma _7}$
as algebraic variables. Consequently, substituting these expressions of the coefficients
![]() $u_{ij}$
in
$u_{ij}$
in
![]() $w_1=0$
results in
$w_1=0$
results in
![]() $w_2(\!\sin \theta _{\alpha _1}$
,
$w_2(\!\sin \theta _{\alpha _1}$
,
![]() $\cos \theta _{\alpha _1})= 0$
, which is a polynomial of total degree
$\cos \theta _{\alpha _1})= 0$
, which is a polynomial of total degree
![]() $22$
in
$22$
in
![]() $\sin \theta _{\alpha _1}$
and
$\sin \theta _{\alpha _1}$
and
![]() $\cos \theta _{\alpha _1}$
. The maximum degrees of
$\cos \theta _{\alpha _1}$
. The maximum degrees of
![]() $\cos \theta _{\alpha _1}$
and
$\cos \theta _{\alpha _1}$
and
![]() $\sin \theta _{\alpha _1}$
in
$\sin \theta _{\alpha _1}$
in
![]() $w_2(\theta _{\alpha _1})$
are 4 and 22, respectively. Subsequently,
$w_2(\theta _{\alpha _1})$
are 4 and 22, respectively. Subsequently,
![]() $w_2$
is reduced to a linear function of
$w_2$
is reduced to a linear function of
![]() $\cos \theta _{\alpha _1}$
using the identities mentioned in (61), which is represented as
$\cos \theta _{\alpha _1}$
using the identities mentioned in (61), which is represented as
![]() $w_s(\!\sin \theta _{\alpha _1}$
,
$w_s(\!\sin \theta _{\alpha _1}$
,
![]() $\cos \theta _{\alpha _1})= 0$
. Furthermore, the coefficients of each term of the form
$\cos \theta _{\alpha _1})= 0$
. Furthermore, the coefficients of each term of the form
![]() $\sin ^{n_s}\theta _{\alpha _1}\cos ^{n_c}\theta _{\alpha _1}$
, where
$\sin ^{n_s}\theta _{\alpha _1}\cos ^{n_c}\theta _{\alpha _1}$
, where
![]() $n_s, n_c \in \mathbb{N}$
, are isolated and simplified individually (due to the use of the MBC form), which reveals that the coefficients of the following terms vanish identically:
$n_s, n_c \in \mathbb{N}$
, are isolated and simplified individually (due to the use of the MBC form), which reveals that the coefficients of the following terms vanish identically:
![]() $\sin \theta _{\alpha _1}$
,
$\sin \theta _{\alpha _1}$
,
![]() $\cos \theta _{\alpha _1}$
and
$\cos \theta _{\alpha _1}$
and
![]() $\cos \theta _{\alpha _1} \sin \theta _{\alpha _1}$
, and so does the constant term (i.e., the term corresponding to
$\cos \theta _{\alpha _1} \sin \theta _{\alpha _1}$
, and so does the constant term (i.e., the term corresponding to
![]() $n_c = n_s = 0$
). Once again, identification of such structural properties of the polynomial has been made possible only due to the application of specialised symbolic simplification routines, and it leads to a factorisation of
$n_c = n_s = 0$
). Once again, identification of such structural properties of the polynomial has been made possible only due to the application of specialised symbolic simplification routines, and it leads to a factorisation of
![]() $w_s=0$
in the following manner, which was otherwise intractable using the default routines provided by the CAS due to extreme complexity of the computations involved:
$w_s=0$
in the following manner, which was otherwise intractable using the default routines provided by the CAS due to extreme complexity of the computations involved:
In (73),
![]() $\xi (\theta _{\alpha _1})$
is a polynomial of total degree
$\xi (\theta _{\alpha _1})$
is a polynomial of total degree
![]() $20$
in
$20$
in
![]() $\sin \theta _{\gamma _7}$
and
$\sin \theta _{\gamma _7}$
and
![]() $\cos \theta _{\gamma _7}$
. Moreover, (73) reduces to
$\cos \theta _{\gamma _7}$
. Moreover, (73) reduces to
![]() $\xi (\theta _{\alpha _1})=0$
as
$\xi (\theta _{\alpha _1})=0$
as
![]() $\sin \theta _{\alpha _1} \neq 0$
, as explained in the context of (63). Subsequently, the equation
$\sin \theta _{\alpha _1} \neq 0$
, as explained in the context of (63). Subsequently, the equation
![]() $\xi =0$
is converted to its algebraic form, in terms of
$\xi =0$
is converted to its algebraic form, in terms of
![]() $t_1=\tan (\theta _{\alpha _1}/2)$
, to obtain an IKU of degree
$t_1=\tan (\theta _{\alpha _1}/2)$
, to obtain an IKU of degree
![]() $40$
,
$40$
,
![]() $v(t_1)=0$
, in the new unknown
$v(t_1)=0$
, in the new unknown
![]() $t_1$
:
$t_1$
:
It may be appreciated at this point that without the detailed multi-step and specialised symbolic manipulations and simplifications, the explicit understanding of the structure of the polynomial equations involved and their factorisations would not have been possible. Consequently, one would have obtained an IKU of degree
![]() $52$
, as noted before. Because of all the steps mentioned above, the final polynomial equation has been obtained in its minimal degree, without any spurious roots.Footnote
19
Furthermore, in (74), the coefficients
$52$
, as noted before. Because of all the steps mentioned above, the final polynomial equation has been obtained in its minimal degree, without any spurious roots.Footnote
19
Furthermore, in (74), the coefficients
![]() $\vartheta _i$
are explicit symbolic functions of the task-space coordinates, which ensures that the nature of the analysis is generic over the entire task space. Consequently, the expressions of the coefficients are huge in their sizes,Footnote
20
as listed below (in GBs), starting from that of
$\vartheta _i$
are explicit symbolic functions of the task-space coordinates, which ensures that the nature of the analysis is generic over the entire task space. Consequently, the expressions of the coefficients are huge in their sizes,Footnote
20
as listed below (in GBs), starting from that of
![]() $\vartheta _0$
, running through to
$\vartheta _0$
, running through to
![]() $\vartheta _{40}$
:
$\vartheta _{40}$
:
 \begin{align} &\left \{ 0.872, 1.691, 4.228, 7.515, 13.393, 20.658, 30.779, 41.951, 55.085, 67.850, 80.946, 91.987,\right .\nonumber \\ & \left. 102.013, 109.060, 114.839, 117.865, 120.333, 120.874, 121.749, 121.380, 70.737, 121.380, \right .\nonumber \\ &\left. 121.749, 120.874, 120.333, 117.865, 114.839, 109.060, 102.013, 91.987, 80.946, 67.850,\right. \nonumber \\ &\left. 55.085, 41.951, 30.779, 20.658, 13.393, 7.515, 4.228, 1.691, 0.872\right \}\!. \end{align}
\begin{align} &\left \{ 0.872, 1.691, 4.228, 7.515, 13.393, 20.658, 30.779, 41.951, 55.085, 67.850, 80.946, 91.987,\right .\nonumber \\ & \left. 102.013, 109.060, 114.839, 117.865, 120.333, 120.874, 121.749, 121.380, 70.737, 121.380, \right .\nonumber \\ &\left. 121.749, 120.874, 120.333, 117.865, 114.839, 109.060, 102.013, 91.987, 80.946, 67.850,\right. \nonumber \\ &\left. 55.085, 41.951, 30.779, 20.658, 13.393, 7.515, 4.228, 1.691, 0.872\right \}\!. \end{align}
The above-mentioned large-sized expressions could only be manipulated by expressing them as polynomials in the nested canonical form (see ref. [Reference Bandyopadhyay and Ghosal24], Section 3, for the details) in the position coordinates of the end-effector,
![]() $\boldsymbol{{p}}$
, such that each of their coefficients reduced to only a few kilobytes in size and is solely in terms of the trigonometric functions of the Euler angles expressing the orientation of the end-effector frame. This improvisation not only reduces the computational complexity involved in simplification but also leads to significant reduction in sizes of the subsequent expressions.
$\boldsymbol{{p}}$
, such that each of their coefficients reduced to only a few kilobytes in size and is solely in terms of the trigonometric functions of the Euler angles expressing the orientation of the end-effector frame. This improvisation not only reduces the computational complexity involved in simplification but also leads to significant reduction in sizes of the subsequent expressions.
Table III. Values of the architecture parameters (see Fig. 1) of the manipulator used for the numerical examples.

The IKU equation is derived and solved in the context of a numerical example in Section 5.2, and the results are presented in Table VI and Fig. 4. Furthermore, due to the symbolic nature of the IKU, its discriminant,
![]() $\Delta _2$
, may be computed as below, the vanishing of which is the condition for a repeated root of the IKU, implying a singularity.
$\Delta _2$
, may be computed as below, the vanishing of which is the condition for a repeated root of the IKU, implying a singularity.
The corresponding singularity is discussed in Case 6 of Section 6.2.
With the knowledge of
![]() $40$
solutions of
$40$
solutions of
![]() $\theta _{\alpha _1}$
from the solution of the IKU equation, the corresponding solutions of
$\theta _{\alpha _1}$
from the solution of the IKU equation, the corresponding solutions of
![]() $\theta _{\gamma _7}, \psi _{6L}, \theta _{23L}, \phi _{5L}$
and
$\theta _{\gamma _7}, \psi _{6L}, \theta _{23L}, \phi _{5L}$
and
![]() $\theta _{2L}$
are obtained from Eqs. (37) and (60), Eqs. (33), (46), and (47), Eqs. (22), (23) and (38), respectively, leading to a set of
$\theta _{2L}$
are obtained from Eqs. (37) and (60), Eqs. (33), (46), and (47), Eqs. (22), (23) and (38), respectively, leading to a set of
![]() $40$
solutions of the variables
$40$
solutions of the variables
![]() $\{\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{23L}, \phi _{5L}, \theta _{2L}\}$
.
$\{\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{23L}, \phi _{5L}, \theta _{2L}\}$
.
4.7. Calculation of the remaining unknown variables
In the following, a procedure for obtaining the variables which remain unknown till this point, that is,
![]() $\theta _{2R}, \theta _{23R},$
$\theta _{2R}, \theta _{23R},$
![]() $\phi _{4L}, \phi _{4R}, \phi _{5R},$
and
$\phi _{4L}, \phi _{4R}, \phi _{5R},$
and
![]() $\phi _{6R}$
, is explained.
$\phi _{6R}$
, is explained.
Equations (26) and (28) are linear in the sine and cosine of the angles
![]() $\theta _{2R}$
and
$\theta _{2R}$
and
![]() $\theta _{23R}$
. Hence, the expressions of
$\theta _{23R}$
. Hence, the expressions of
![]() $\cos \theta _{23R}$
and
$\cos \theta _{23R}$
and
![]() $\sin \theta _{23R}$
are calculated from Eqs. (26) and (28), respectively:
$\sin \theta _{23R}$
are calculated from Eqs. (26) and (28), respectively:
 \begin{align} &\cos \theta _{23R}=\frac{\varepsilon _1(\theta _{\gamma _7}, \theta _{2R})}{l_3}, \quad \sin \theta _{23R}=\frac{\varepsilon _2(\theta _{\alpha _1}, \theta _{\gamma _7}, \theta _{2R})}{l_3},\, \textrm{since} \, l_3 \neq 0, \, \textrm{and} \nonumber\\ &\varepsilon _1(\theta _{\gamma _7}, \theta _{2R})\,{:\!=}\, p_z+(d_7-l_w \sin \kappa )\cos \beta + (a_6-l_w \cos \kappa ) \sin \beta \cos \theta _{\gamma _7} -l_2 \cos \theta _{2R}, \end{align}
\begin{align} &\cos \theta _{23R}=\frac{\varepsilon _1(\theta _{\gamma _7}, \theta _{2R})}{l_3}, \quad \sin \theta _{23R}=\frac{\varepsilon _2(\theta _{\alpha _1}, \theta _{\gamma _7}, \theta _{2R})}{l_3},\, \textrm{since} \, l_3 \neq 0, \, \textrm{and} \nonumber\\ &\varepsilon _1(\theta _{\gamma _7}, \theta _{2R})\,{:\!=}\, p_z+(d_7-l_w \sin \kappa )\cos \beta + (a_6-l_w \cos \kappa ) \sin \beta \cos \theta _{\gamma _7} -l_2 \cos \theta _{2R}, \end{align}
Thereafter, substituting the expressions of
![]() $\cos \theta _{23R}$
and
$\cos \theta _{23R}$
and
![]() $\sin \theta _{23R}$
from (77) in the identity
$\sin \theta _{23R}$
from (77) in the identity
![]() $\cos ^2\theta _{23R}+ \sin ^2\theta _{23R}=1$
results in equation
$\cos ^2\theta _{23R}+ \sin ^2\theta _{23R}=1$
results in equation
![]() $o(\theta _{\alpha _1}, \theta _{\gamma _7}, \theta _{2R})=0$
:
$o(\theta _{\alpha _1}, \theta _{\gamma _7}, \theta _{2R})=0$
:
In (79), the coefficients
![]() $o_i$
are functions of
$o_i$
are functions of
![]() $\theta _{\alpha _1}$
and
$\theta _{\alpha _1}$
and
![]() $\theta _{\gamma _7}$
. Subsequently, the equation is solved for known values of
$\theta _{\gamma _7}$
. Subsequently, the equation is solved for known values of
![]() $\theta _{\alpha _1}$
and
$\theta _{\alpha _1}$
and
![]() $\theta _{\gamma _7}$
, resulting in
$\theta _{\gamma _7}$
, resulting in
![]() $80$
solutions of the variables
$80$
solutions of the variables
![]() $\{\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{23L}, \phi _{5L}, \theta _{2L}, \theta _{23R}$
,
$\{\theta _{\alpha _1}, \theta _{\gamma _7}, \psi _{6L}, \theta _{23L}, \phi _{5L}, \theta _{2L}, \theta _{23R}$
,
![]() $\theta _{2R}\}$
, in the general case. It may be noticed that a singularity is encountered when
$\theta _{2R}\}$
, in the general case. It may be noticed that a singularity is encountered when
![]() $o_1^2+o_2^2-o_3^2$
vanishes, as the solutions of the variables
$o_1^2+o_2^2-o_3^2$
vanishes, as the solutions of the variables
![]() $\theta _{2R}$
and
$\theta _{2R}$
and
![]() $\theta _{23R}$
merge in this condition. This is discussed in detail in Section 6.2, in Case 7.
$\theta _{23R}$
merge in this condition. This is discussed in detail in Section 6.2, in Case 7.
The remaining passive joint variables, namely
![]() $\phi _{4L}, \phi _{4R}, \phi _{5R}$
and
$\phi _{4L}, \phi _{4R}, \phi _{5R}$
and
![]() $\phi _{6R}$
may be obtained using Eqs. (11), (14)–(16), for the known values of the active joint angles and the passive joint angles
$\phi _{6R}$
may be obtained using Eqs. (11), (14)–(16), for the known values of the active joint angles and the passive joint angles
![]() $\phi _{5L}, \phi _{6L}$
. Since the solution procedure for calculating the passive joint variables for the known active joint angles has previously been covered as part of the FKP in Section 3, the corresponding details are not presented here again for the sake of brevity. While the variable
$\phi _{5L}, \phi _{6L}$
. Since the solution procedure for calculating the passive joint variables for the known active joint angles has previously been covered as part of the FKP in Section 3, the corresponding details are not presented here again for the sake of brevity. While the variable
![]() $\phi _{4L}$
has a unique solution, the variables
$\phi _{4L}$
has a unique solution, the variables
![]() $\phi _{4R}, \phi _{5R}$
and
$\phi _{4R}, \phi _{5R}$
and
![]() $\phi _{6R}$
have two sets of solutions. Thus, in total, the IKP leads to a total of
$\phi _{6R}$
have two sets of solutions. Thus, in total, the IKP leads to a total of
![]() $160$
solutions (including complex ones) for a generic pose of the end-effector in
$160$
solutions (including complex ones) for a generic pose of the end-effector in
![]() $\mathbb{SE}$
(3).
$\mathbb{SE}$
(3).
It may be noted, however, that even though the total number of solutions is rather high at
![]() $160$
, the actual physical situation is not really as complex. There are only
$160$
, the actual physical situation is not really as complex. There are only
![]() $40$
main/independent branches of solutions, which is not uncharacteristically high in the domain of kinematics, as the general
$40$
main/independent branches of solutions, which is not uncharacteristically high in the domain of kinematics, as the general
![]() $6$
-
$6$
-
![]() $6$
-Stewart platform manipulator has the same number of solutions for its FKP [Reference Husty25], and the SNU 3-UPU has
$6$
-Stewart platform manipulator has the same number of solutions for its FKP [Reference Husty25], and the SNU 3-UPU has
![]() $78$
solutions to its FKP [Reference Walter, Husty and Pfurner26]. Within each of these
$78$
solutions to its FKP [Reference Walter, Husty and Pfurner26]. Within each of these
![]() $40$
main branches, four sub-branches appear, two of which essentially correspond to the elbow-up and elbow-down configurations of the right 2-R arm at the elbow joint
$40$
main branches, four sub-branches appear, two of which essentially correspond to the elbow-up and elbow-down configurations of the right 2-R arm at the elbow joint
![]() ${\boldsymbol{{e}}}_R$
. It is interesting that the other two sub-branches, which are attributed to the spherical joint at
${\boldsymbol{{e}}}_R$
. It is interesting that the other two sub-branches, which are attributed to the spherical joint at
![]() $\boldsymbol{{p}}_R$
, result in the same physical configuration of the manipulator, as seen in Fig. 4. Thus, one can summarise the situation as having
$\boldsymbol{{p}}_R$
, result in the same physical configuration of the manipulator, as seen in Fig. 4. Thus, one can summarise the situation as having
![]() $40$
branches of solution, each with two possible configurations of the right arm.
$40$
branches of solution, each with two possible configurations of the right arm.
5. Numerical examples
In this section, the theoretical developments presented so far are illustrated via numerical examples. The FKP is solved first for a given set of inputs. The resulting pose of the manipulator is used as the input to the IKP, which provides an intrinsic means of validating the results of both. The values of the architecture parameters used are listed in Table III. All the lengths and angles mentioned in this paper are measured in metres and radians, respectively. Real values, such as
![]() $0.5$
and
$0.5$
and
![]() $2.69$
, have been replaced by
$2.69$
, have been replaced by
![]() $\frac{1}{2}$
and
$\frac{1}{2}$
and
![]() $\frac{269}{100}$
, respectively, to take advantage of the exact arithmetic computations afforded by the CAS employed, as opposed to the default floating-point operations.
$\frac{269}{100}$
, respectively, to take advantage of the exact arithmetic computations afforded by the CAS employed, as opposed to the default floating-point operations.
5.1. Forward kinematics
The numerical values of the active joint angles are chosen as
![]() $\theta _1 = \dfrac{\pi }{10}$
,
$\theta _1 = \dfrac{\pi }{10}$
,
![]() $\theta _{2L} = \dfrac{\pi }{3}$
,
$\theta _{2L} = \dfrac{\pi }{3}$
,
![]() $\theta _{3L} = \dfrac{\pi }{6}$
,
$\theta _{3L} = \dfrac{\pi }{6}$
,
![]() $\theta _{2R} = \dfrac{\pi }{6}$
,
$\theta _{2R} = \dfrac{\pi }{6}$
,
![]() $\theta _{3R} = \dfrac{\pi }{3}$
and
$\theta _{3R} = \dfrac{\pi }{3}$
and
![]() $\theta _7 = \dfrac{\pi }{4}$
. The values of the passive joint angles obtained are listed in Table IV, and the corresponding poses of the manipulator are depicted in Fig. 2. It is interesting to note that two distinct branches of solutions to the FKP result in identical poses of the manipulator (as indicated in the subcaptions in Fig. 2). In other words, mathematically speaking, there are eight branches to the solutions of FKP, which manifest, in the general case, only as four distinct physical poses. This is due to the parametrisation of the passive spherical joint at
$\theta _7 = \dfrac{\pi }{4}$
. The values of the passive joint angles obtained are listed in Table IV, and the corresponding poses of the manipulator are depicted in Fig. 2. It is interesting to note that two distinct branches of solutions to the FKP result in identical poses of the manipulator (as indicated in the subcaptions in Fig. 2). In other words, mathematically speaking, there are eight branches to the solutions of FKP, which manifest, in the general case, only as four distinct physical poses. This is due to the parametrisation of the passive spherical joint at
![]() $\boldsymbol{{p}}_R$
in terms of the variables
$\boldsymbol{{p}}_R$
in terms of the variables
![]() $\phi _{4R}, \phi _{5R}$
and
$\phi _{4R}, \phi _{5R}$
and
![]() $\phi _{6R}$
, which correspond to a set of Euler angles, which allow two distinct sets of values to describe the same physical orientation. Specifying the active variables
$\phi _{6R}$
, which correspond to a set of Euler angles, which allow two distinct sets of values to describe the same physical orientation. Specifying the active variables
![]() $\{\theta _1,\theta _{2L}, \theta _{2R},\theta _{3L}, \theta _{3R} \}$
locates
$\{\theta _1,\theta _{2L}, \theta _{2R},\theta _{3L}, \theta _{3R} \}$
locates
![]() $\boldsymbol{{p}}_L$
and
$\boldsymbol{{p}}_L$
and
![]() $\boldsymbol{{p}}_R$
uniquely in space. Therefore, the 2-R chain
$\boldsymbol{{p}}_R$
uniquely in space. Therefore, the 2-R chain
![]() $\boldsymbol{{p}}_L\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R$
can be assembled, in general, in two different manners, analogous to the “elbow-up” and “elbow-down” configurations appearing in the IK of planar 2-R manipulators, as seen in the poses 1 (or 5) and 3 (or 7), in Fig. 3(a). These configurations of the chain
$\boldsymbol{{p}}_L\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R$
can be assembled, in general, in two different manners, analogous to the “elbow-up” and “elbow-down” configurations appearing in the IK of planar 2-R manipulators, as seen in the poses 1 (or 5) and 3 (or 7), in Fig. 3(a). These configurations of the chain
![]() $\boldsymbol{{p}}_L$
$\boldsymbol{{p}}_L$
![]() $\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R$
, being mirror-symmetric about the line
$\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R$
, being mirror-symmetric about the line
![]() $\boldsymbol{{p}}_L\boldsymbol{{p}}_R$
, share the same plane. This is reflected by the common value of
$\boldsymbol{{p}}_L\boldsymbol{{p}}_R$
, share the same plane. This is reflected by the common value of
![]() $\phi _{4L}$
between these two branches (see Table IV), since the orientation of the plane containing the chain
$\phi _{4L}$
between these two branches (see Table IV), since the orientation of the plane containing the chain
![]() $\boldsymbol{{p}}_L\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R$
is governed by
$\boldsymbol{{p}}_L\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R$
is governed by
![]() $\phi _{4L}$
. As may be expected, these geometric conditions continue to hold good when the passive joint variable
$\phi _{4L}$
. As may be expected, these geometric conditions continue to hold good when the passive joint variable
![]() $\phi _{4L}$
undergoes a change by
$\phi _{4L}$
undergoes a change by
![]() $\pm \pi$
starting from its value at pose 1 (or,
$\pm \pi$
starting from its value at pose 1 (or,
![]() $3, 5, 7$
) results in the pose 2 (or
$3, 5, 7$
) results in the pose 2 (or
![]() $4,6,8$
, respectively), as seen in poses 1 and 2, in Fig. 3(b). The same is reflected in the values of
$4,6,8$
, respectively), as seen in poses 1 and 2, in Fig. 3(b). The same is reflected in the values of
![]() $\phi _{4L}$
, as seen in Table IV.
$\phi _{4L}$
, as seen in Table IV.
Table IV. Forward kinematics solutions for
![]() $\theta _1 = \frac{\pi }{10}$
,
$\theta _1 = \frac{\pi }{10}$
,
![]() $\theta _{2L} = \frac{\pi }{3}$
,
$\theta _{2L} = \frac{\pi }{3}$
,
![]() $\theta _{3L} = \frac{\pi }{6}$
,
$\theta _{3L} = \frac{\pi }{6}$
,
![]() $\theta _{2R} = \frac{\pi }{6}$
,
$\theta _{2R} = \frac{\pi }{6}$
,
![]() $\theta _{3R} = \frac{\pi }{3}$
and
$\theta _{3R} = \frac{\pi }{3}$
and
![]() $\theta _7 = \frac{\pi }{4}$
, the corresponding poses of which are displayed in Fig. 2.
$\theta _7 = \frac{\pi }{4}$
, the corresponding poses of which are displayed in Fig. 2.


Figure 3. Geometric relations between some of the FK branches shown in Fig. 2. The view angles have been chosen so as to enhance the visual clarity in the 2-D figures.
Each branch of solution is validated numerically by substituting them back in the original constraint equations, namely Eqs. (6) and (13), and computing their residue as the vector
![]() $\boldsymbol{\eta }_{FK}= [\boldsymbol{\eta }_{FKL},\boldsymbol{\eta }_{FKR}]^\top$
. A scalar measure of error,
$\boldsymbol{\eta }_{FK}= [\boldsymbol{\eta }_{FKL},\boldsymbol{\eta }_{FKR}]^\top$
. A scalar measure of error,
![]() $e_{FK}$
, is then introduced via the norm of this residue:
$e_{FK}$
, is then introduced via the norm of this residue:
The solutions are deemed accurate if
![]() $e_{\textrm FK} \le 10^{-10}$
. The last column of Table IV tabulates the actual values of
$e_{\textrm FK} \le 10^{-10}$
. The last column of Table IV tabulates the actual values of
![]() $e_{\textrm FK}$
corresponding to all the branches of solutions.
$e_{\textrm FK}$
corresponding to all the branches of solutions.
A Mathematica “demonstration” (i.e., a GUI) has been developed to simulate finite inputs at the active joints and to visualise the corresponding motions via on-screen animation. A simple example is captured in the video file animation_forward_kinematics_H6A.mp4, wherein each joint is jogged, albeit virtually, over finite ranges of inputs by manipulating individual sliders.
5.2. Inverse kinematics
The end-effector pose defined by
![]() $\alpha = 1.19556$
,
$\alpha = 1.19556$
,
![]() $\beta = 2.27373$
,
$\beta = 2.27373$
,
![]() $\gamma = -1.27501$
,
$\gamma = -1.27501$
,
![]() $p_x = 5.17431$
,
$p_x = 5.17431$
,
![]() $p_y = 1.03851$
and
$p_y = 1.03851$
and
![]() $p_z = 2.72026$
, obtained in the first and fifth branches of forward kinematic solutions in Table IV of Section 5.1, is used as input for performing the IKP.
$p_z = 2.72026$
, obtained in the first and fifth branches of forward kinematic solutions in Table IV of Section 5.1, is used as input for performing the IKP.
As mentioned in Section 4, the symbolic expressions of the coefficients of the IKU equation (see (74)) are huge in size (see (75)). Therefore, even though these expressions are exact in nature, the numerical values they yield after substitution of input variables as floating point numbers may incorporate significant error, due to accumulation of truncation errors associated with floating-point arithmetic. Hence, floating-point numbers are replaced by their rational approximations (accurate up to the fifth digit after the decimal), in order to pursue numerical computations in the exact form, to the extent possible. The resulting IKU equation, that is, the numerical version of (74), is expressed in the monic Footnote 21 form and its coefficients, truncated to the fifth place after the decimal, are presented in Table V.
Table V. Monic form of the IKU in (74) for
![]() $\alpha =1.19556$
,
$\alpha =1.19556$
,
![]() $\beta =2.27373$
,
$\beta =2.27373$
,
![]() $\gamma =-1.27501$
,
$\gamma =-1.27501$
,
![]() $p_x = 5.17431$
,
$p_x = 5.17431$
,
![]() $p_y = 1.03851$
and
$p_y = 1.03851$
and
![]() $p_z = 2.72026$
.
$p_z = 2.72026$
.

The IKU equation has been solved using the built-in routine Solve of Mathematica.
The values of joint angles corresponding to the real roots of the IKU are listed in Table VI, and the poses of the manipulator corresponding to the branches are shown in Fig. 4. Similar to the solutions of FKP, it may be seen here that a pair branches of mathematical solutions of the IKP result in the same physical pose (see Table VI and Fig. 4). The IKP solutions can also be grouped pairwise into elbow-up and elbow-down configurations of the right arm, as can be seen, for example, in Fig. 4(a) and (b), respectively, the said elbow joint being located at
![]() ${{\boldsymbol{{e}}}}_R$
.
${{\boldsymbol{{e}}}}_R$
.
Table VI. Inverse kinematics solutions for
![]() $\alpha = 1.19556$
,
$\alpha = 1.19556$
,
![]() $\beta = 2.27373$
,
$\beta = 2.27373$
,
![]() $\gamma = -1.27501$
,
$\gamma = -1.27501$
,
![]() $p_x = 5.17431$
,
$p_x = 5.17431$
,
![]() $p_y = 1.03851$
and
$p_y = 1.03851$
and
![]() $p_z = 2.72026$
, the corresponding poses of which are displayed in Fig. 4.
$p_z = 2.72026$
, the corresponding poses of which are displayed in Fig. 4.


Figure 4. Poses depicting the real solutions to the inverse kinematic problem for the given inputs (enumerated as per the rows of Table VI).

Figure 5. A schematic depicting the setup for the trajectory-tracking simulation. The manipulator is depicted at the initial point of the path, which is chosen to be pose 1 shown in Fig. 2(a), conforming to FK branch
![]() $1$
in Table IV. The path corresponding to this branch of FK, which is computed first as per the actuator inputs given by Eq. (82), is shown by magenta dots. It is subsequently tracked by the manipulator, following the IK branch 9, whose initial point is listed in Table VI. The evolution of the end-effector frame,
$1$
in Table IV. The path corresponding to this branch of FK, which is computed first as per the actuator inputs given by Eq. (82), is shown by magenta dots. It is subsequently tracked by the manipulator, following the IK branch 9, whose initial point is listed in Table VI. The evolution of the end-effector frame,
![]() $\boldsymbol{{x}}_e\boldsymbol{{y}}_e\boldsymbol{{z}}_e$
, is shown by the triad of mutually orthogonal arrows in the RGB convention, with “R” denoting
$\boldsymbol{{x}}_e\boldsymbol{{y}}_e\boldsymbol{{z}}_e$
, is shown by the triad of mutually orthogonal arrows in the RGB convention, with “R” denoting
![]() ${{\boldsymbol{{X}}}}$
, and so on. Only a few sets of target frames are shown to avoid clutter. The simulation has been captured in the video file animation_inverse_kinematics_H6A.mp4 associated with this paper. (Reference to colours pertain to the digital version of this article.)
${{\boldsymbol{{X}}}}$
, and so on. Only a few sets of target frames are shown to avoid clutter. The simulation has been captured in the video file animation_inverse_kinematics_H6A.mp4 associated with this paper. (Reference to colours pertain to the digital version of this article.)
As in the case of the FKP, a scalar measure of error is defined by referring back to the original constraint equations, namely Eqs. (18) and (25):
However, due to much greater complexity of computations involved in this case, for example, the solution of the
![]() $40$
-degree IKU equation, the acceptable limit on the error is set at
$40$
-degree IKU equation, the acceptable limit on the error is set at
![]() $e_{IK} \le 10^{-5}$
. It may be noted that this limit is adequately small for these computations, as it is seen, for example, the inverse kinematic solution branches (
$e_{IK} \le 10^{-5}$
. It may be noted that this limit is adequately small for these computations, as it is seen, for example, the inverse kinematic solution branches (
![]() $9$
,
$9$
,
![]() $10$
) in Table VI match with the corresponding forward kinematic solution branches, namely (
$10$
) in Table VI match with the corresponding forward kinematic solution branches, namely (
![]() $1$
,
$1$
,
![]() $5$
) in Table IV, up to the fourth place after the decimal. The last column of Table VI lists the measure of error in each branch of solution.
$5$
) in Table IV, up to the fourth place after the decimal. The last column of Table VI lists the measure of error in each branch of solution.
5.3. Forward and inverse kinematics along joint-space trajectories
In the above, the results obtained in the FK and IK analyses have been validated for their numerical accuracies by evaluating their residues independently, and also by checking one against the other for a given set of inputs. In the following, the same is repeated for a finite span of motion of the manipulator, by making it follow a given trajectory in its active joint space. Without any loss of generality, it is assumed that the manipulator starts from rest and also comes to a complete halt at the end of the trajectory.
The initial configuration of the robot is chosen to be pose
![]() $1$
shown in Fig. 2(a) that belongs to FK branch
$1$
shown in Fig. 2(a) that belongs to FK branch
![]() $1$
in Table IV. The set of active angles in this configuration is denoted by
$1$
in Table IV. The set of active angles in this configuration is denoted by
![]() ${\boldsymbol{\theta }}_{\textrm{I}}$
. For the final pose, the active angles, given by
${\boldsymbol{\theta }}_{\textrm{I}}$
. For the final pose, the active angles, given by
![]() ${\boldsymbol{\theta }}_{\textrm{F}} = [\theta _{1_{\textrm{F}}}, \theta _{2L_{\textrm{F}}}, \theta _{2R_{\textrm{F}}}, \theta _{3L_{\textrm{F}}}, \theta _{3R_{\textrm{F}}}, \theta _{7_{\textrm{F}}}]^\top = \left [-\dfrac{7\pi }{30}, \dfrac{\pi }{6}, 0, \dfrac{\pi }{2}, \dfrac{7\pi }{12}, \dfrac{5\pi }{12}\right ]^\top$
, are chosen arbitrarily. Nevertheless, care is taken to ensure (by visual inspection) that the links of the manipulator do not interfere while executing this trajectory.
${\boldsymbol{\theta }}_{\textrm{F}} = [\theta _{1_{\textrm{F}}}, \theta _{2L_{\textrm{F}}}, \theta _{2R_{\textrm{F}}}, \theta _{3L_{\textrm{F}}}, \theta _{3R_{\textrm{F}}}, \theta _{7_{\textrm{F}}}]^\top = \left [-\dfrac{7\pi }{30}, \dfrac{\pi }{6}, 0, \dfrac{\pi }{2}, \dfrac{7\pi }{12}, \dfrac{5\pi }{12}\right ]^\top$
, are chosen arbitrarily. Nevertheless, care is taken to ensure (by visual inspection) that the links of the manipulator do not interfere while executing this trajectory.
The active joint variables at any time
![]() $t \in [0, T_{\textrm{m}}]$
are obtained by a cubic interpolation of
$t \in [0, T_{\textrm{m}}]$
are obtained by a cubic interpolation of
![]() ${\boldsymbol{\theta }}_{\textrm{I}}$
and
${\boldsymbol{\theta }}_{\textrm{I}}$
and
![]() ${\boldsymbol{\theta }}_{\textrm{F}}$
, subjected to the static end conditions mentioned above:
${\boldsymbol{\theta }}_{\textrm{F}}$
, subjected to the static end conditions mentioned above:
where
![]() $T_{\textrm{m}}$
is the duration of motion. Equation (82) is used to sample
$T_{\textrm{m}}$
is the duration of motion. Equation (82) is used to sample
![]() ${\boldsymbol{\theta }}(t)$
uniformly at
${\boldsymbol{\theta }}(t)$
uniformly at
![]() $n$
points (
$n$
points (
![]() $n$
being
$n$
being
![]() $50$
in the present case), to obtain
$50$
in the present case), to obtain
![]() $n$
sets of inputs to the FK problem, denoted by
$n$
sets of inputs to the FK problem, denoted by
![]() ${\boldsymbol{\theta }}_i ={\boldsymbol{\theta }}(iT_{\textrm{m}}/n), i=1,2,\dots,n$
. For each
${\boldsymbol{\theta }}_i ={\boldsymbol{\theta }}(iT_{\textrm{m}}/n), i=1,2,\dots,n$
. For each
![]() ${\boldsymbol{\theta }}_i$
, FK is performed following the solution procedure presented in Section 3 to determine the end-effector coordinates,
${\boldsymbol{\theta }}_i$
, FK is performed following the solution procedure presented in Section 3 to determine the end-effector coordinates,
![]() ${{\boldsymbol{{X}}}}_i = [x_i, y_i, z_i, \alpha _i, \beta _i, \gamma _i]$
. All the passive angles are also computed in the process. The variations in the angles
${{\boldsymbol{{X}}}}_i = [x_i, y_i, z_i, \alpha _i, \beta _i, \gamma _i]$
. All the passive angles are also computed in the process. The variations in the angles
![]() $\phi _{4L}$
,
$\phi _{4L}$
,
![]() $\phi _{4R}$
,
$\phi _{4R}$
,
![]() $\phi _{5L}$
,
$\phi _{5L}$
,
![]() $\phi _{5R}$
,
$\phi _{5R}$
,
![]() $\phi _{6L}$
and
$\phi _{6L}$
and
![]() $\phi _{6R}$
w.r.t. time are plotted in Fig. 6. Among the eight FK branches obtained for each
$\phi _{6R}$
w.r.t. time are plotted in Fig. 6. Among the eight FK branches obtained for each
![]() ${\boldsymbol{\theta }}_i$
, only the first branch (i.e., corresponding to the first row in Table IV) is considered at all the time instances, since the initial pose corresponds to this branch. These plots provide the references for the IK solutions to be validated.
${\boldsymbol{\theta }}_i$
, only the first branch (i.e., corresponding to the first row in Table IV) is considered at all the time instances, since the initial pose corresponds to this branch. These plots provide the references for the IK solutions to be validated.

Figure 6. Variations of the passive joint angles with time, as obtained from forward and inverse kinematic analysis. The IK branch
![]() $9$
retraces the FK branch
$9$
retraces the FK branch
![]() $1$
, as expected, the apparent mismatch in the values of
$1$
, as expected, the apparent mismatch in the values of
![]() $\phi _{6L}$
being due to a difference of
$\phi _{6L}$
being due to a difference of
![]() $2\pi$
, which is trivial. It may also be noted that in the cases of
$2\pi$
, which is trivial. It may also be noted that in the cases of
![]() $\phi _{4R}$
and
$\phi _{4R}$
and
![]() $\phi _{6R}$
, IK branch
$\phi _{6R}$
, IK branch
![]() $10$
differs from the IK branch
$10$
differs from the IK branch
![]() $9$
by
$9$
by
![]() $\pi$
, while they have the opposite signs in the case of
$\pi$
, while they have the opposite signs in the case of
![]() $\phi _{5L}$
.
$\phi _{5L}$
.
Inverse kinematic analysis is performed next, using as inputs the end-effector coordinates,
![]() ${{\boldsymbol{{X}}}}_i$
, found in the FK process. From Table VI, it may be seen that the initial pose corresponds to the
${{\boldsymbol{{X}}}}_i$
, found in the FK process. From Table VI, it may be seen that the initial pose corresponds to the
![]() $9$
th branch of the IK solutions, making it the obvious choice for tracking and superposing the results in Fig. 6. As expected, this branch of IK agrees at all the points with the reference, that is, FK branch
$9$
th branch of the IK solutions, making it the obvious choice for tracking and superposing the results in Fig. 6. As expected, this branch of IK agrees at all the points with the reference, that is, FK branch
![]() $1$
. Another branch of IK, namely the
$1$
. Another branch of IK, namely the
![]() $10$
th, is also included in the said figure. While this branch is not supposed to match the reference trajectories in all the variables, it has certain interesting relations with it, as noted in the caption of Fig. 6.
$10$
th, is also included in the said figure. While this branch is not supposed to match the reference trajectories in all the variables, it has certain interesting relations with it, as noted in the caption of Fig. 6.
Computationally, the tracking of the different IK branches is achieved by solving Eqs. (32)–(37) at each point
![]() ${{\boldsymbol{{X}}}}_i$
using the routine FindRoot available in Mathematica. It uses an iterative technique, and it is found that the IK solution at the previous point,
${{\boldsymbol{{X}}}}_i$
using the routine FindRoot available in Mathematica. It uses an iterative technique, and it is found that the IK solution at the previous point,
![]() ${{\boldsymbol{{X}}}}_{i-1}$
, serves as a successful initial guess while computing
${{\boldsymbol{{X}}}}_{i-1}$
, serves as a successful initial guess while computing
![]() ${{\boldsymbol{{X}}}}_i$
in all the instances. These computations, as summarised visually in Fig. 6, provide conclusive validations of the computational methods proposed in this article, and the results obtained thereof.
${{\boldsymbol{{X}}}}_i$
in all the instances. These computations, as summarised visually in Fig. 6, provide conclusive validations of the computational methods proposed in this article, and the results obtained thereof.
In the next section, the singularity conditions obtained while solving the FKP and IKP, in Sections 3, 4, respectively, are studied in detail.
6. Analysis of singularities in the forward and inverse kinematics
The analysis of loop-closure equations of a manipulator leads to the solution of its FKP and IKP, as seen in the previous sections. In this section, the special cases identified in that process, that is, poses at which pairs of branches of solutions merge, are discussed in detail.
It is helpful to initiate this discussion considering the general case first. Therefore, the loop-closure constraints in Eqs. (19)–(25) and Eqs. (26)–(31) are represented as:
Differentiating (83) with respect to time,
![]() $t$
, one obtains
$t$
, one obtains
In the case of the H6A manipulator, the constraint equations are scleronomic (see, e.g., ref. [Reference Udwadia and Kalaba27], pp. 74), that is, they have no explicit dependence on time. Hence, (84) reduces to (85), which relates the output velocity,
![]() $\dot{\boldsymbol{{x}}}$
, to the input velocity,
$\dot{\boldsymbol{{x}}}$
, to the input velocity,
![]() $\dot{{\boldsymbol{\theta }}}$
, and the passive joint velocity,
$\dot{{\boldsymbol{\theta }}}$
, and the passive joint velocity,
![]() $\dot{{\boldsymbol{\phi }}}$
:
$\dot{{\boldsymbol{\phi }}}$
:
There are many definitions and corresponding classifications of kinematic singularities. In the following, two types of singularities would be discussed, following refs. [Reference Ghosal and Ravani28], [Reference Bandyopadhyay and Ghosal29], namely the loss- and the gain-type of singularities. The loss-type singularity is defined here w.r.t. the end-effector, which loses one or more DoF at such a singularity. The gain-type singularity, as the name suggests, leads to a gain of one or more DoF, which manifests either at the end-effector or at some other passive link(s), or both.
-
Loss-type singularities: The loss-type singularity occurs when a non-zero input fails to produce any output at the end-effector, that is,
 $\dot{{\boldsymbol{\theta }}} \ne{\textbf{0}}$
but
$\dot{{\boldsymbol{\theta }}} \ne{\textbf{0}}$
but
 $\dot{\boldsymbol{{x}}} ={\textbf{0}}$
. Therefore, (85) reduces to:(86)
$\dot{\boldsymbol{{x}}} ={\textbf{0}}$
. Therefore, (85) reduces to:(86) \begin{align} &{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\theta }}}\dot{{\boldsymbol{\theta }}} +{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\phi }}}\dot{{\boldsymbol{\phi }}} ={\textbf{0}}; \end{align}
Since
\begin{align} &{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\theta }}}\dot{{\boldsymbol{\theta }}} +{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\phi }}}\dot{{\boldsymbol{\phi }}} ={\textbf{0}}; \end{align}
Since \begin{align*} \nonumber \Rightarrow &{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}} \dot{{{\boldsymbol{{q}}}}} = \mathbf{0}, \quad \textrm{where} \;\;{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}} \,{:\!=}\, \left [{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\theta }}} \;{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\phi }}}\right ] \in{\mathbb{R}}^{12 \times 12} \, \textrm{and}\,{{\boldsymbol{{q}}}} = [{\boldsymbol{\theta }}^\top,{\boldsymbol{\phi }}^\top ]^\top. \end{align*}
\begin{align*} \nonumber \Rightarrow &{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}} \dot{{{\boldsymbol{{q}}}}} = \mathbf{0}, \quad \textrm{where} \;\;{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}} \,{:\!=}\, \left [{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\theta }}} \;{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\phi }}}\right ] \in{\mathbb{R}}^{12 \times 12} \, \textrm{and}\,{{\boldsymbol{{q}}}} = [{\boldsymbol{\theta }}^\top,{\boldsymbol{\phi }}^\top ]^\top. \end{align*}
 $\dot{{\boldsymbol{\theta }}} \ne{\textbf{0}}$
(as mentioned above),
$\dot{{\boldsymbol{\theta }}} \ne{\textbf{0}}$
(as mentioned above),
 $\dot{{\boldsymbol{{q}}}} \ne{\textbf{0}}$
, too. Hence, the condition for loss-type singularity is obtained as:(87)It may be noted that (86) may be satisfied even when
$\dot{{\boldsymbol{{q}}}} \ne{\textbf{0}}$
, too. Hence, the condition for loss-type singularity is obtained as:(87)It may be noted that (86) may be satisfied even when \begin{align} &{\operatorname{det}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}) = 0.} \end{align}
\begin{align} &{\operatorname{det}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}) = 0.} \end{align}
 $\dot{\boldsymbol{{x}}} \ne{\textbf{0}}$
, iff
$\dot{\boldsymbol{{x}}} \ne{\textbf{0}}$
, iff
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}\boldsymbol{{x}}}$
is also singular, and
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}\boldsymbol{{x}}}$
is also singular, and
 $\dot{\boldsymbol{{x}}} \in \operatorname{nullspace}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}\boldsymbol{{x}}})$
.
$\dot{\boldsymbol{{x}}} \in \operatorname{nullspace}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}\boldsymbol{{x}}})$
.
-
Gain-type singularities: The manipulator is said to encounter a gain-type singularity when the end-effector and/or the passive link(s) acquire an infinitesimal or finite motion capability, that is, either
 $\dot{\boldsymbol{{x}}} \ne{\textbf{0}}$
or
$\dot{\boldsymbol{{x}}} \ne{\textbf{0}}$
or
 $\dot{{\boldsymbol{\phi }}} \ne{\textbf{0}}$
, or both, even when the actuators are held fixed, that is,
$\dot{{\boldsymbol{\phi }}} \ne{\textbf{0}}$
, or both, even when the actuators are held fixed, that is,
 $\dot{{\boldsymbol{\theta }}} ={\textbf{0}}$
. Therefore, at a gain-type singularity, (85) reduces to:(88)Since
$\dot{{\boldsymbol{\theta }}} ={\textbf{0}}$
. Therefore, at a gain-type singularity, (85) reduces to:(88)Since \begin{align} &{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}} \dot{{\boldsymbol{\xi }}}=\textbf{0}, \, \textrm{where}\,{\boldsymbol{\xi }} = [\boldsymbol{{x}}^\top,{\boldsymbol{\phi }}^\top ]^\top, \, \textrm{and hence,} \,{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}} \,{:\!=}\, \left [{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}\boldsymbol{{x}}} \;{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\phi }}}\right ] \in \mathbb{R}^{12\times 12}. \end{align}
\begin{align} &{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}} \dot{{\boldsymbol{\xi }}}=\textbf{0}, \, \textrm{where}\,{\boldsymbol{\xi }} = [\boldsymbol{{x}}^\top,{\boldsymbol{\phi }}^\top ]^\top, \, \textrm{and hence,} \,{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}} \,{:\!=}\, \left [{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}\boldsymbol{{x}}} \;{{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\phi }}}\right ] \in \mathbb{R}^{12\times 12}. \end{align}
 $\dot{{\boldsymbol{\xi }}} \ne{\textbf{0}}$
as at least one of
$\dot{{\boldsymbol{\xi }}} \ne{\textbf{0}}$
as at least one of
 $\dot{\boldsymbol{{x}}}$
and
$\dot{\boldsymbol{{x}}}$
and
 $\dot{{\boldsymbol{\phi }}}$
is/are non-zero, the condition for gain-type singularities may be derived as:(89)As in the case of loss-type singularities, in this case, (88) holds good for
$\dot{{\boldsymbol{\phi }}}$
is/are non-zero, the condition for gain-type singularities may be derived as:(89)As in the case of loss-type singularities, in this case, (88) holds good for \begin{align} &\operatorname{det}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}) = 0. \end{align}
\begin{align} &\operatorname{det}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}) = 0. \end{align}
 $\dot{{\boldsymbol{\theta }}} \ne{\textbf{0}}$
, iff
$\dot{{\boldsymbol{\theta }}} \ne{\textbf{0}}$
, iff
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\theta }}}$
is also singular, and
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\theta }}}$
is also singular, and
 $\dot{{\boldsymbol{\theta }}} \in \operatorname{nullspace}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\theta }}})$
.
$\dot{{\boldsymbol{\theta }}} \in \operatorname{nullspace}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\theta }}})$
.
Furthermore, the manipulator encounters loss-type and gain-type singularities simultaneously in the case when
![]() ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}} \dot{{{\boldsymbol{{q}}}}} = \mathbf{0}$
and
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}} \dot{{{\boldsymbol{{q}}}}} = \mathbf{0}$
and
![]() ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}\dot{{\boldsymbol{\xi }}}=\textbf{0}$
together, that is,
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}\dot{{\boldsymbol{\xi }}}=\textbf{0}$
together, that is,
![]() $\operatorname{det}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}) = 0$
(see (87)) and
$\operatorname{det}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}) = 0$
(see (87)) and
![]() $\operatorname{det}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}) = 0$
(see (89)).
$\operatorname{det}({{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}) = 0$
(see (89)).
The singularities observed during the analyses of the FKP and the IKP are explained in the context of loss and gain of DoF in the following. Certain architecture singularities (i.e., special architectures, at which all poses can be singular in one or more ways) also appeared in the course of the mathematical analysis. Some of these are trivial in nature, for example, those which require the vanishing of the parameters
![]() $l_2, l_3, l_w$
, which are ignored as these are not feasible physically. Some others are of practical interest, and these have been discussed in detail in the appropriate context.
$l_2, l_3, l_w$
, which are ignored as these are not feasible physically. Some others are of practical interest, and these have been discussed in detail in the appropriate context.
6.1. Singularity conditions arising out of forward kinematic analysis
The singularity conditions gleaned from the study of the FKP are revisited in this subsection. The specific cases are enumerated hereafter.
-
Case 1:
 $\sin \dfrac{\phi _{6L}}{2}=0$
or
$\sin \dfrac{\phi _{6L}}{2}=0$
or
 $\sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right )=0$
. It is noticed that either of the conditions
$\sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right )=0$
. It is noticed that either of the conditions
 $\sin \dfrac{\phi _{6L}}{2}=0$
or
$\sin \dfrac{\phi _{6L}}{2}=0$
or
 $\sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right )=0$
leads to the architecture singularity of
$\sin \left (\phi _{5L}+\dfrac{\phi _{6L}}{2}\right )=0$
leads to the architecture singularity of
 $d_2=0$
(see (6)), which causes simultaneous rank deficiency of the Jacobian matrices
$d_2=0$
(see (6)), which causes simultaneous rank deficiency of the Jacobian matrices
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}$
. However, this singularity is not relevant for the H6A manipulator, as its architecture ensures that the two arms always lie in parallel planes at a mutual distance of
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}$
. However, this singularity is not relevant for the H6A manipulator, as its architecture ensures that the two arms always lie in parallel planes at a mutual distance of
 $2d_2 \gt 0$
(see Table III).
$2d_2 \gt 0$
(see Table III). -
Case 2:
 $\sin \phi _{5R}=0$
. It is interesting to note that this condition is akin to that of gimbal lock in the context of Euler angles, due to the representation of the spherical joint, leading to a loss-type singularity. This singularity is analogous to the “wrist singularity” associated with the wrist-decoupled 6-R spatial manipulators, such as PUMA 560 (see, e.g., ref. [Reference Ghosal1], pp. 79). The condition
$\sin \phi _{5R}=0$
. It is interesting to note that this condition is akin to that of gimbal lock in the context of Euler angles, due to the representation of the spherical joint, leading to a loss-type singularity. This singularity is analogous to the “wrist singularity” associated with the wrist-decoupled 6-R spatial manipulators, such as PUMA 560 (see, e.g., ref. [Reference Ghosal1], pp. 79). The condition
 $\sin \phi _{5R}=0$
leads to at least one of the two following conditions (refer to (13)):
$\sin \phi _{5R}=0$
leads to at least one of the two following conditions (refer to (13)):
 $\cos \phi _{4L}=0$
, and
$\cos \phi _{4L}=0$
, and
 $\sin (\phi _{5L}+\phi _{6L})=0$
, which are discussed separately in the following.
$\sin (\phi _{5L}+\phi _{6L})=0$
, which are discussed separately in the following.
-
1.
 $\cos \phi _{4L}=0$
. The condition
$\cos \phi _{4L}=0$
. The condition
 $\cos \phi _{4L}=0$
, together with
$\cos \phi _{4L}=0$
, together with
 $\sin \phi _{5R}=0$
, yet again yields the architecture singularity
$\sin \phi _{5R}=0$
, yet again yields the architecture singularity
 $d_2=0$
(see (6)) and results in the degeneracy of
$d_2=0$
(see (6)) and results in the degeneracy of
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}$
.
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}$
. -
2.
 $\sin (\phi _{5L}+\phi _{6L})=0$
. In this case, too, the Jacobian matrices
$\sin (\phi _{5L}+\phi _{6L})=0$
. In this case, too, the Jacobian matrices
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}$
lose rank, leading to a coincidence of the gain- and loss-type of singularities. As may be seen in Fig. 7(a), the links
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}$
lose rank, leading to a coincidence of the gain- and loss-type of singularities. As may be seen in Fig. 7(a), the links
 $\boldsymbol{{p}}_L{\boldsymbol{{p}}}$
and
$\boldsymbol{{p}}_L{\boldsymbol{{p}}}$
and
 $\boldsymbol{{p}}\boldsymbol{{p}}_R$
become collinear indicating the merger of two configurations of the sub-chain
$\boldsymbol{{p}}\boldsymbol{{p}}_R$
become collinear indicating the merger of two configurations of the sub-chain
 $\boldsymbol{{p}}_L\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R$
which would lie on either side of the line
$\boldsymbol{{p}}_L\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R$
which would lie on either side of the line
 $\boldsymbol{{p}}_L\boldsymbol{{p}}_R$
in the absence of this singularity. It may be verified that the point
$\boldsymbol{{p}}_L\boldsymbol{{p}}_R$
in the absence of this singularity. It may be verified that the point
 $\boldsymbol{{p}}$
gains an infinitesimal translational DoF along a line perpendicular to both the line
$\boldsymbol{{p}}$
gains an infinitesimal translational DoF along a line perpendicular to both the line
 $\boldsymbol{{p}}_L\boldsymbol{{p}}_R$
and the axis of the passive rotary joint at
$\boldsymbol{{p}}_L\boldsymbol{{p}}_R$
and the axis of the passive rotary joint at
 $\boldsymbol{{p}}$
. This DoF is independent of all the actuators.
$\boldsymbol{{p}}$
. This DoF is independent of all the actuators.

Figure 7. The joint angles of the pose in Fig. 7(a) are
![]() $\theta _1=0.31416, \theta _{2L}=1.04720, \theta _{3L}=-2.48784,$
$\theta _1=0.31416, \theta _{2L}=1.04720, \theta _{3L}=-2.48784,$
![]() $\theta _{2R}=-1.40982,\ \theta _{3R}=-3.17242,\ \theta _7=0.78540,\ \phi _{4L}=-1.04720,\ \phi _{5L}=0,\ \phi _{6L}=3.14159,\ \phi _{4R}=$
$\theta _{2R}=-1.40982,\ \theta _{3R}=-3.17242,\ \theta _7=0.78540,\ \phi _{4L}=-1.04720,\ \phi _{5L}=0,\ \phi _{6L}=3.14159,\ \phi _{4R}=$
![]() $ 1.04720, \phi _{5R}=0$
and
$ 1.04720, \phi _{5R}=0$
and
![]() $\phi _{6R}=3.14159$
and the architecture parameters are mentioned in Table III. For Fig. 7(b), the joint angles are
$\phi _{6R}=3.14159$
and the architecture parameters are mentioned in Table III. For Fig. 7(b), the joint angles are
![]() $\theta _1=-2.35619,$
$\theta _1=-2.35619,$
![]() $\theta _{2L}=0.12378, \theta _{3L}=4.29217, \theta _{2R}=-0.46959,$
$\theta _{2L}=0.12378, \theta _{3L}=4.29217, \theta _{2R}=-0.46959,$
![]() $\theta _{3R}=4.80511, \theta _7=-2.32155, \phi _{4L}=-3.14159,\ \phi _{5L}= 1.57080,$
$\theta _{3R}=4.80511, \theta _7=-2.32155, \phi _{4L}=-3.14159,\ \phi _{5L}= 1.57080,$
![]() $\phi _{6L}=-2.09440, \phi _{4R}=3.00331,$
$\phi _{6L}=-2.09440, \phi _{4R}=3.00331,$
![]() $\phi _{5R}=0.52917$
and
$\phi _{5R}=0.52917$
and
![]() $\phi _{6R}=0.15984$
,
$\phi _{6R}=0.15984$
,
![]() $l_w=1.1547$
and the rest of the architecture parameters is mentioned in Table III. Similarly, the poses of the manipulator in Fig. 7(c) are for the joint angles
$l_w=1.1547$
and the rest of the architecture parameters is mentioned in Table III. Similarly, the poses of the manipulator in Fig. 7(c) are for the joint angles
![]() $\theta _1=0.31416,\ \theta _{2L}=1.04720,\ \theta _{3L}=0.52360,\ \theta _{2R}=1.01576,\ \theta _{3R}=0,\ \theta _7=0.78540,\ \phi _{4L}=-0.98233,$
$\theta _1=0.31416,\ \theta _{2L}=1.04720,\ \theta _{3L}=0.52360,\ \theta _{2R}=1.01576,\ \theta _{3R}=0,\ \theta _7=0.78540,\ \phi _{4L}=-0.98233,$
![]() $ \phi _{5L}=0.13389, \phi _{6L}=2.38188, \phi _{4R}=0.04002, \phi _{5R}=2.81015$
and
$ \phi _{5L}=0.13389, \phi _{6L}=2.38188, \phi _{4R}=0.04002, \phi _{5R}=2.81015$
and
![]() $\phi _{6R}=1.11732$
and the architecture parameters are mentioned in Table III.
$\phi _{6R}=1.11732$
and the architecture parameters are mentioned in Table III.
6.2. Singularity conditions arising out of inverse kinematic analysis
The physical significance of the singularity conditions obtained from the study of the IKP is studied in this subsection. The specific cases are listed below.
-
Case 1:
 $i_1^2+j_1^2-k_1^2=0$
and
$i_1^2+j_1^2-k_1^2=0$
and
 $i_2^2+j_2^2-k_2^2=0$
(see Eqs. (40) and (41), respectively). When these conditions are satisfied simultaneously, the compound variable
$i_2^2+j_2^2-k_2^2=0$
(see Eqs. (40) and (41), respectively). When these conditions are satisfied simultaneously, the compound variable
 $(\phi _{5L}+\psi _{6L})$
appears in identical pairs in the solutions of IKP of the manipulator. It is interesting to note that the condition,
$(\phi _{5L}+\psi _{6L})$
appears in identical pairs in the solutions of IKP of the manipulator. It is interesting to note that the condition,
 $\tau = 0$
(see (71)), exemplifies such a situation, which, in turn, has the following consequences:(90)Both the Jacobian matrices
$\tau = 0$
(see (71)), exemplifies such a situation, which, in turn, has the following consequences:(90)Both the Jacobian matrices \begin{align} \tau =0 \Rightarrow \begin{array}{cc}\left ( \begin{array}{ll} \cos \theta _{\alpha _1}=0, \\ \cos \beta \sin \theta _{\alpha _1}=0. \\ \end{array}\right. \end{array} \end{align}
\begin{align} \tau =0 \Rightarrow \begin{array}{cc}\left ( \begin{array}{ll} \cos \theta _{\alpha _1}=0, \\ \cos \beta \sin \theta _{\alpha _1}=0. \\ \end{array}\right. \end{array} \end{align}
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}$
lose rank under these conditions. Figure 7(b) shows an example of such a singularity, in which it is observed that the loss of a DoF is attributed to the fact that the axis of active rotary joint at
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{\boldsymbol{\xi }}}$
lose rank under these conditions. Figure 7(b) shows an example of such a singularity, in which it is observed that the loss of a DoF is attributed to the fact that the axis of active rotary joint at
 ${{\boldsymbol{{e}}}}$
is parallel to those of the other active rotary joints on the left chain, namely
${{\boldsymbol{{e}}}}$
is parallel to those of the other active rotary joints on the left chain, namely
 ${{\boldsymbol{{s}}}}_L$
and
${{\boldsymbol{{s}}}}_L$
and
 ${{\boldsymbol{{e}}}}_L$
. It is also found that these conditions lead to the vanishing of
${{\boldsymbol{{e}}}}_L$
. It is also found that these conditions lead to the vanishing of
 $\psi _{6L}$
and, finally, forms an architecture singularity, given by:(91)
$\psi _{6L}$
and, finally, forms an architecture singularity, given by:(91) \begin{align} l_w \sin \kappa = 2 d_2. \end{align}
\begin{align} l_w \sin \kappa = 2 d_2. \end{align}
As long as this condition is satisfied, this kind of singularity would occur on a finite-dimensional subspace of the workspace of the manipulator.
-
Case 2:
 $a_1 b_2 - a_2 b_1=0$
(refer to (47)). It may be observed that the condition
$a_1 b_2 - a_2 b_1=0$
(refer to (47)). It may be observed that the condition
 $a_1 b_2 - a_2 b_1=0$
is trivially satisfied when
$a_1 b_2 - a_2 b_1=0$
is trivially satisfied when
 $a_1=0$
and
$a_1=0$
and
 $b_1=0$
, which also make
$b_1=0$
, which also make
 $\mu$
vanish as per (48). In (44),
$\mu$
vanish as per (48). In (44),
 $a_1=\sin \beta \sin \theta _{\gamma _7}$
and
$a_1=\sin \beta \sin \theta _{\gamma _7}$
and
 $b_1=-(\!\cos \theta _{\gamma _7} \sin \theta _{\alpha _1}+\cos \beta \cos \theta _{\alpha _1} \sin \theta _{\gamma _7})$
. Hence, vanishing of
$b_1=-(\!\cos \theta _{\gamma _7} \sin \theta _{\alpha _1}+\cos \beta \cos \theta _{\alpha _1} \sin \theta _{\gamma _7})$
. Hence, vanishing of
 $a_1, b_1$
simultaneously leads to two subcases: (a)
$a_1, b_1$
simultaneously leads to two subcases: (a)
 $\beta =0, \theta _{\alpha _1}=-\theta _{\gamma _7}$
and (b)
$\beta =0, \theta _{\alpha _1}=-\theta _{\gamma _7}$
and (b)
 $\theta _{\alpha _1}=0, \theta _{\gamma _7}=0$
. The former subcase is equivalent to gimbal lock at the end-effector due to the representation of the orientation using Euler angles. This is a parametric singularity and has been mentioned previously in Case 2 in Section 6.2. Interestingly, both the subcases result in a loss-type singularity, as seen in the loss of rank of
$\theta _{\alpha _1}=0, \theta _{\gamma _7}=0$
. The former subcase is equivalent to gimbal lock at the end-effector due to the representation of the orientation using Euler angles. This is a parametric singularity and has been mentioned previously in Case 2 in Section 6.2. Interestingly, both the subcases result in a loss-type singularity, as seen in the loss of rank of
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
, and also lead to the architecture singularity,
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
, and also lead to the architecture singularity,
 $d_2 = 0$
. However, in this case, the architecture singularity is not associated with a coincidence of loss-type and gain-type of singularities, as in the Cases 1 and 2 discussed previously in Section 6.1.
$d_2 = 0$
. However, in this case, the architecture singularity is not associated with a coincidence of loss-type and gain-type of singularities, as in the Cases 1 and 2 discussed previously in Section 6.1. -
Case 3:
 $a_2^2+b_2^2-c_2^2=0$
(see (45)). This singularity corresponds to the merging of the elbow-up and elbow-down configurations of the planar 2-R sub-chain
$a_2^2+b_2^2-c_2^2=0$
(see (45)). This singularity corresponds to the merging of the elbow-up and elbow-down configurations of the planar 2-R sub-chain
 ${\boldsymbol{{s}}}_L{\boldsymbol{{e}}}_L$
-
${\boldsymbol{{s}}}_L{\boldsymbol{{e}}}_L$
-
 ${{\boldsymbol{{e}}}}_L\boldsymbol{{p}}_L$
, as evidenced by the vanishing of
${{\boldsymbol{{e}}}}_L\boldsymbol{{p}}_L$
, as evidenced by the vanishing of
 $\sin \theta _{3L}$
and the consequent loss of rank of
$\sin \theta _{3L}$
and the consequent loss of rank of
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
. In this case, the point
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
. In this case, the point
 $\boldsymbol{{p}}_L$
loses its ability to translate along the direction of the links
$\boldsymbol{{p}}_L$
loses its ability to translate along the direction of the links
 ${{\boldsymbol{{s}}}}_L{{\boldsymbol{{e}}}}_L$
and
${{\boldsymbol{{s}}}}_L{{\boldsymbol{{e}}}}_L$
and
 ${{\boldsymbol{{e}}}}_L\boldsymbol{{p}}_L$
.
${{\boldsymbol{{e}}}}_L\boldsymbol{{p}}_L$
. -
Case 4:
 $b_3^2-4a_3 c_3=0$
and
$b_3^2-4a_3 c_3=0$
and
 $b_4^2-4a_4 c_4=0$
(refer to Eqs. (54) and (55), respectively). Iff satisfied simultaneously, these conditions force a pair of values of the variable
$b_4^2-4a_4 c_4=0$
(refer to Eqs. (54) and (55), respectively). Iff satisfied simultaneously, these conditions force a pair of values of the variable
 $\psi _{6L}$
to merge in the solutions of IKP of the manipulator, causing a singularity in the matrix
$\psi _{6L}$
to merge in the solutions of IKP of the manipulator, causing a singularity in the matrix
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and consequently, the loss of a DoF. Interestingly, this case is observed to be satisfied when
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
and consequently, the loss of a DoF. Interestingly, this case is observed to be satisfied when
 $\mu = 0$
(see (48)), which requires vanishing of
$\mu = 0$
(see (48)), which requires vanishing of
 $d_2$
, just as in Case 2 above.
$d_2$
, just as in Case 2 above. -
Case 5:
 $\Delta _1 = 0$
and
$\Delta _1 = 0$
and
 $b_5^2-4a_5 c_5=0$
(see Eqs. (67) and (68), respectively). In this case, variable
$b_5^2-4a_5 c_5=0$
(see Eqs. (67) and (68), respectively). In this case, variable
 $\theta _{\gamma _7}$
acquires a pair of repeated values in the solution of the IKP of the manipulator, resulting in a loss-type singularity. This is also reflected in the singularity of the Jacobian matrix
$\theta _{\gamma _7}$
acquires a pair of repeated values in the solution of the IKP of the manipulator, resulting in a loss-type singularity. This is also reflected in the singularity of the Jacobian matrix
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
.
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
. -
Case 6:
 $\Delta _2 = 0$
(see (76)). This condition corresponds to the merger of the solutions of the variable
$\Delta _2 = 0$
(see (76)). This condition corresponds to the merger of the solutions of the variable
 $\theta _{\alpha _1}$
, leading to a loss-type singularity, as reflected in the rank deficiency of the Jacobian matrix
$\theta _{\alpha _1}$
, leading to a loss-type singularity, as reflected in the rank deficiency of the Jacobian matrix
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
.
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
. -
Case 7:
 $o_1^2+o_2^2-o_3^2=0$
(refer to (79)). This condition indicates the merger of the elbow-up and elbow-down configurations of the 2-R sub-chain
$o_1^2+o_2^2-o_3^2=0$
(refer to (79)). This condition indicates the merger of the elbow-up and elbow-down configurations of the 2-R sub-chain
 ${{\boldsymbol{{s}}}}_R{{\boldsymbol{{e}}}}_R$
-
${{\boldsymbol{{s}}}}_R{{\boldsymbol{{e}}}}_R$
-
 ${{\boldsymbol{{e}}}}_R\boldsymbol{{p}}_R$
which causes
${{\boldsymbol{{e}}}}_R\boldsymbol{{p}}_R$
which causes
 $\sin \theta _{3R}$
to vanish. It is obvious (see Fig. 7(c)) that in this case the point
$\sin \theta _{3R}$
to vanish. It is obvious (see Fig. 7(c)) that in this case the point
 $\boldsymbol{{p}}_R$
cannot have any motion along the said links for any combination of actuator inputs. As expected, this loss of DoF is confirmed by the degeneracy of the matrix
$\boldsymbol{{p}}_R$
cannot have any motion along the said links for any combination of actuator inputs. As expected, this loss of DoF is confirmed by the degeneracy of the matrix
 ${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
.
${{\boldsymbol{{J}}}}_{{{\boldsymbol{{g}}}}{{\boldsymbol{{q}}}}}$
.
7. Discussions
As mentioned before, the kinematics of the H6A is significantly challenging because of two reasons: (a) incorporation of multi-DoF passive joints in its architecture and (b) the asymmetry of the two limbs constituting the manipulator – while the left arm has a universal joint just before the wrist assembly, the right one has a spherical joint. Interestingly, in this case, the IKP is much more complicated than the FKP. Therefore, these two problems are addressed in a manner which is found to be best suited for them individually, starting from different sets of equations depicting the kinematic constraints. This approach is perhaps not the most common in the kinematic analyses of hybrid and parallel robots.
The solution to the FKP has only eight branches, all of which could be obtained in the closed form (see Section 3). The IKP has 160 solutions, which were obtained by first reducing the problem to the solution of a univariate polynomial equation of degree 40, as shown in Section 4. While this approach of reducing a set of simultaneous loop-closure equations to a univariate equation of higher degree is indeed common in manipulator kinematics, a significant distinction of the computational approach presented in this paper vis-à-vis most others is that the coefficients of the said polynomial were obtained as closed-form symbolic expressions in terms of the original inputs, that is, the pose variables
![]() $\{x,y,z,\alpha,\beta,\gamma \}$
. In doing so, it is ensured that the results obtained are fully generic over the workspace of the manipulator. It is, therefore, established conclusively that the H6A manipulator has
$\{x,y,z,\alpha,\beta,\gamma \}$
. In doing so, it is ensured that the results obtained are fully generic over the workspace of the manipulator. It is, therefore, established conclusively that the H6A manipulator has
![]() $160$
solutions for the IKP in the complex plane, and
$160$
solutions for the IKP in the complex plane, and
![]() $8$
for the FKP, for any possible set of inputs.
$8$
for the FKP, for any possible set of inputs.
Another useful consequence of the exact symbolic approach is that all the special configurations associated with the FKP and IKP are identified analytically. At these configurations, there are certain breakdowns in the solution procedure arising out of the merger of different branches of kinematics. Such configurations are analysed further to categorise them into loss-type, gain-type and architecture singularities (see Section 6). Most of the architecture singularities requiring certain link lengths to vanish are avoided naturally, as in the actual manipulator these lengths are not zeros (see Case 1 in Section 6.1 and Cases 2 and 4 in Section 6.2). However, in Case 1 discussed in Section 6.2, a very important condition is derived, which is non-trivial in nature, namely Eq. (91). It shows that the architecture parameters
![]() $d_2$
,
$d_2$
,
![]() $l_w$
and
$l_w$
and
![]() $\kappa$
cannot be chosen arbitrarily, but in a manner so as not to satisfy (91). It turns out that for the given values of
$\kappa$
cannot be chosen arbitrarily, but in a manner so as not to satisfy (91). It turns out that for the given values of
![]() $d_2$
and
$d_2$
and
![]() $\kappa$
in Table III, this architecture singularity occurs at
$\kappa$
in Table III, this architecture singularity occurs at
![]() $l_w = 1.1547$
, which is distinct from the actual architecture of the manipulator, where
$l_w = 1.1547$
, which is distinct from the actual architecture of the manipulator, where
![]() $l_w =1$
, but not very far from it.
$l_w =1$
, but not very far from it.
It may be mentioned here that the closed-form analytical results summarised above could only be derived at the cost of a huge amount of symbolic computations and several improvisations, the details of which may be found in Section 4. Specially designed algorithms to simplify large expressions constituted of trigonometric and algebraic subexpressions were employed in these computations, since a direct application of the default general-purpose routines of the CAS used proved to be grossly inadequate for this purpose. In particular, the elimination of the variables
![]() $\psi _{6L}$
and
$\psi _{6L}$
and
![]() $\theta _{\gamma _7}$
from Eqs. (20), (48) and Eqs. (27), (60), respectively, demanded a customised approach, involving careful observation and exploitation of the special structures appearing in some expressions, specifically:
$\theta _{\gamma _7}$
from Eqs. (20), (48) and Eqs. (27), (60), respectively, demanded a customised approach, involving careful observation and exploitation of the special structures appearing in some expressions, specifically:
-
Deriving (48) from (46) by rearranging and taking square roots brought down the size of the equation
 $p=0$
in (53) from
$p=0$
in (53) from
 $6.110$
MB to
$6.110$
MB to
 $19.232$
KB
$19.232$
KB -
Using the identities in (61) facilitated:
-
Rewriting the polynomial equations as shown in (69) and (70) enabled the factoring of the polynomial
 $\tau$
(see (72)) and dropped the degree of the IKU by
$\tau$
(see (72)) and dropped the degree of the IKU by
 $8$
. Moreover, it also led to the identification of the singularity caused by the vanishing of the polynomial
$8$
. Moreover, it also led to the identification of the singularity caused by the vanishing of the polynomial
 $\tau$
.
$\tau$
.
Even with these computational concoctions, the sizes of the final expressions, for example the coefficients of the univariate polynomial representing the IKP, sum up to 2760.873 GB. Without these customised tools and improvisations, it may not have been possible to derive these expressions in the closed form.
These symbolic computations, leading to the derivation of the univariate polynomial equation representing the IKP and the analysis of the singularities associated with the FKP and IKP, form the contributions of this paper.
8. Conclusions
This paper presents a comprehensive study of a novel six-DoF spatial manipulator of hybrid architecture named H6A. The manipulator has two arms originating from a rigid “waist” which can swivel about a fixed vertical axis. The arms join at the other end to form a wrist assembly. Asymmetry in the architecture of the arms due to the presence of different multi-DoF passive joints in each makes the kinematics of the manipulator complicated enough to be of sufficient interest. While the FKP is solved easily to obtain all the eight solutions in the closed form, the IKP proves to be much harder, with a total of
![]() $160$
solutions in the general case. Through extensive symbolic computations, this problem is reduced to that of solving a
$160$
solutions in the general case. Through extensive symbolic computations, this problem is reduced to that of solving a
![]() $40$
-degree polynomial equation. The coefficients of this polynomial are obtained as closed-form symbolic expressions of the corresponding inputs, which establishes the generic nature of the solutions. The results obtained are numerically validated by computing the residues of the original equations, as well as using the solutions of the forward kinematics in the inverse kinematics. The symbolic nature of the analysis presented in the paper affords the identification of the associated singularities in a natural manner, that is, by obtaining the conditions for the merger of the kinematic branches. This exact symbolic computation approach to kinematic analysis may be helpful in studying other hybrid/parallel manipulators.
$40$
-degree polynomial equation. The coefficients of this polynomial are obtained as closed-form symbolic expressions of the corresponding inputs, which establishes the generic nature of the solutions. The results obtained are numerically validated by computing the residues of the original equations, as well as using the solutions of the forward kinematics in the inverse kinematics. The symbolic nature of the analysis presented in the paper affords the identification of the associated singularities in a natural manner, that is, by obtaining the conditions for the merger of the kinematic branches. This exact symbolic computation approach to kinematic analysis may be helpful in studying other hybrid/parallel manipulators.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/ S0263574723000334.
Acknowledgements
The authors thank Dr Jagannath Raju, CTO, and Mr Sharachchandra Bhat, ex-employee, Systemantics India Pvt. Ltd., Bengaluru, India, for sharing with them the architecture data listed in Table III. They also thank Mr Bibekananda Patra, doctoral student at the Department of Engineering Design, Indian Institute of Technology Madras, for creating the GUI demonstrating the forward kinematics and the corresponding video.
Author contributions
The problem statement was perceived by PG and SB. The analysis and computations were performed by PG and SR, under the guidance of SB. The paper was written by PG, SR and SB.
Financial support
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Competing interest
The authors declare no conflicts of interest exist.
Ethical standards
Not applicable under the heading.
A. Calculation of the degree-of-freedom of the H6A manipulator
As stated in ref. [Reference Shoham and Roth30], the mobility of a mechanism with closed loops, that is, the DoF, attributed to both Grübler and Kutzbach, is defined by:
In the above equation,
![]() $l$
is the total number of independent loops,
$l$
is the total number of independent loops,
![]() $p$
is the total number of joints and
$p$
is the total number of joints and
![]() $f_i$
is the DoF of the ith joint. The H6A manipulator consists of one independent kinematic loop
$f_i$
is the DoF of the ith joint. The H6A manipulator consists of one independent kinematic loop
![]() ${{\boldsymbol{{o}}}}\textrm{-}{\boldsymbol{{s}}}_L\textrm{-}{\boldsymbol{{e}}}_L\textrm{-}\boldsymbol{{p}}_L\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R\textrm{-}{\boldsymbol{{e}}}_R\textrm{-}{\boldsymbol{{s}}}_R\textrm{-}{{\boldsymbol{{o}}}}$
, therefore,
${{\boldsymbol{{o}}}}\textrm{-}{\boldsymbol{{s}}}_L\textrm{-}{\boldsymbol{{e}}}_L\textrm{-}\boldsymbol{{p}}_L\textrm{-}\boldsymbol{{p}}\textrm{-}\boldsymbol{{p}}_R\textrm{-}{\boldsymbol{{e}}}_R\textrm{-}{\boldsymbol{{s}}}_R\textrm{-}{{\boldsymbol{{o}}}}$
, therefore,
![]() $l=1$
. The DoF corresponding to all the joints are tabulated in Table A1. Thereafter, substituting data from Table A1 gives
$l=1$
. The DoF corresponding to all the joints are tabulated in Table A1. Thereafter, substituting data from Table A1 gives
![]() $M=6$
.
$M=6$
.
Table A1. Joints of the H6A manipulator and their corresponding DoF.