No CrossRef data available.
Published online by Cambridge University Press: 16 October 2024
This study proposes a novel hybrid learning approach for developing a visual path-following algorithm for industrial robots. The process involves three steps: data collection from a simulation environment, network training, and testing on a real robot. The actor network is trained using supervised learning for 500 epochs. A semitrained network is then obtained at the 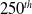 $250^{th}$ epoch. This network is further trained for another 250 epochs using reinforcement learning methods within the simulation environment. Networks trained with supervised learning (500 epochs) and the proposed hybrid learning method (250 epochs each of supervised and reinforcement learning) are compared. The hybrid learning approach achieves a significantly lower average error (30.9 mm) compared with supervised learning (39.3 mm) on real-world images. Additionally, the hybrid approach exhibits faster processing times (31.7 s) compared with supervised learning (35.0 s). The proposed method is implemented on a KUKA Agilus KR6 R900 six-axis robot, demonstrating its effectiveness. Furthermore, the hybrid approach reduces the total power consumption of the robot’s motors compared with the supervised learning method. These results suggest that the hybrid learning approach offers a more effective and efficient solution for visual path following in industrial robots compared with traditional supervised learning.
$250^{th}$ epoch. This network is further trained for another 250 epochs using reinforcement learning methods within the simulation environment. Networks trained with supervised learning (500 epochs) and the proposed hybrid learning method (250 epochs each of supervised and reinforcement learning) are compared. The hybrid learning approach achieves a significantly lower average error (30.9 mm) compared with supervised learning (39.3 mm) on real-world images. Additionally, the hybrid approach exhibits faster processing times (31.7 s) compared with supervised learning (35.0 s). The proposed method is implemented on a KUKA Agilus KR6 R900 six-axis robot, demonstrating its effectiveness. Furthermore, the hybrid approach reduces the total power consumption of the robot’s motors compared with the supervised learning method. These results suggest that the hybrid learning approach offers a more effective and efficient solution for visual path following in industrial robots compared with traditional supervised learning.