1. Introduction
Transfer learning refers to the use of knowledge gained in one or more tasks for new, unseen tasks. In transfer learning, the source task is the origin of the knowledge, while the target tasks are the test tasks that are not seen during training. A robot is required to have generalizable skills in real world. For instance, a bipedal robot is required to be robust against changing ground friction, gravity, and wind condition. Training a robot for all possible scenarios is time-consuming, impractical, and expensive. In order to develop intelligent systems, we expect robots to adequately and quickly transfer the learned model to the new target task. One way to learn a transferable model for robot control is deep reinforcement learning (RL) [Reference Gupta, Eppner, Levine and Abbeel1, Reference Rajeswaran, Kumar, Gupta, Schulman, Todorov and Levine2, Reference Xie, Clary, Dao, Morais, Hurst and van de Panne3, Reference Siekmann, Green, Warila, Fern and Hurst4].
We follow a data-driven RL approach to derive generalizable policies for a humanoid and a hopper robot. Data generation in simulators is inexpensive; hence, learning-based models can learn a diverse set of behaviors to be transferred to the real world. Accordingly, physics-based simulators can integrate specifications of real robots such as contact, joint limit, and actuator constraints. To close the domain gap in RL for transfer, generalization techniques such as domain adaptation are used in training. Our contributions address this step following the large body of work on robust policy gradient algorithms. In ref. [Reference Gangapurwala, Mitchell and Havoutis5], domain randomization techniques are used in a simulator to increase the robustness of the policy prior to the transfer to a physical AnyMAL robot. Koenemann et al. used a physics-based simulator, “Multi-Joint dynamics with Contact” (MuJoCo) [Reference Todorov, Erez and Tassa6], to transfer skills to a physical humanoid robot HRP-2 [Reference Koenemann, Del Prete, Tassa, Todorov, Stasse, Bennewitz and Mansard7]. Many successful applications to the real world [Reference Haarnoja, Zhou, Ha, Tan, Tucker and Levine8, Reference Li, Cheng, Peng, Abbeel, Levine, Berseth and Sreenath9, Reference Ha, Xu, Tan, Levine and Tan10, Reference Gangapurwala, Mitchell and Havoutis5, Reference Hwangbo, Lee, Dosovitskiy, Bellicoso, Tsounis, Koltun and Hutter11, Reference Tan, Zhang, Coumans, Iscen, Bai, Hafner, Bohez and Vanhoucke12, Reference Peng, Coumans, Zhang, Lee, Tan and Levine13] use PPO, which has been evaluated in the humanoid environment of MuJoCo. Other approaches to bipedal locomotion include constrained optimization techniques [Reference Dai, Valenzuela and Tedrake14] and conforming to balance criteria like ZMP [Reference VukobratoviĆ and Borovac15]. However, these methods are suitable for humanoids with flat feet and have low generalizability as discussed in ref. [Reference Li, Cheng, Peng, Abbeel, Levine, Berseth and Sreenath9].
Physics-based simulator accuracy and computational efficiency are an integral part of learning dexterous policies in RL. MuJoCo, a physics engine acquired by DeepMind [Reference Todorov, Erez and Tassa6], realizes a rich and accurate contact model and computes forward and inverse kinematics using the convex Gauss Principle. Active constraints used in MuJoCo are categorized as equality, friction loss, limit, and contact constraints. In addition to the constraints specified by the simulator, the requirements of a physical robot can also be used in policy optimization and reward function as in ref. [Reference Gangapurwala, Mitchell and Havoutis5].
Improving generalization in deep RL is a useful strategy for robust transfer of robot skills. However, assessing generalization in deep RL is challenging due to overfitting. A common method for assessing generalization is to evaluate a deep RL algorithm in another task. Yet, deep RL algorithms, including the policy gradient methods such as Trust Region Policy Optimization (TRPO) [Reference Schulman, Levine, Abbeel, Jordan and Moritz16] and Proximal Policy Optimization (PPO) [Reference Schulman, Wolski, Dhariwal, Radford and Klimov17], have been commonly evaluated based on source task performance. In transfer RL, the best policy in the source task is not necessarily the best and the most robust policy in the target tasks. Policies trained using hyperparameters tuned for the source task are prone to overfitting in the target task. However, some hyperparameters (such as the clipping hyperparameter of PPO, which controls the lower bound for the policy gradient loss) were set to fixed values when evaluating the results in many studies [Reference Fujita and Maeda18, Reference Han and Sung19, Reference Bansal, Pachocki, Sidor, Sutskever and Mordatch20, Reference Al-Shedivat, Bansal, Burda, Sutskever, Mordatch and Abbeel21, Reference Huang, Gu, Wu and Guan22]. The choice of hyperparameters becomes increasingly important because unregularized deep RL algorithms can underperform by overfitting.
Recent works [Reference Tobin, Fong, Ray, Schneider, Zaremba and Abbeel23, Reference Cobbe, Klimov, Hesse, Kim and Schulman24, Reference Zhao, Siguad, Stulp and Hospedales25] have proposed regularization techniques for deep RL to avoid overfitting to a specific task. A common method to improve generalization is domain randomization [Reference Tobin, Fong, Ray, Schneider, Zaremba and Abbeel23], where task parameters are randomized during training. Dropout, L2 regularization, data augmentation, batch normalization, increasing the stochasticity of the policy [Reference Mnih, Badia and Mirza26], and the environment were the regularization techniques used in ref. [Reference Cobbe, Klimov, Hesse, Kim and Schulman24] to increase target task performance. Similar to ref. [Reference Cobbe, Klimov, Hesse, Kim and Schulman24], Zhao et al. [Reference Zhao, Siguad, Stulp and Hospedales25] compared regularization techniques for deep RL such as policy network size reduction, soft actor-critic entropy regularizer [Reference Haarnoja, Zhou, Abbeel and Levine27], multi-domain learning [Reference Tobin, Fong, Ray, Schneider, Zaremba and Abbeel23], structured control net [Reference Srouji, Zhang and Salakhutdinov28], and adversarially robust policy learning (APRL) [Reference Mandlekar, Zhu, Garg, Fei-Fei and Savarese29].
Adversarial algorithms are dynamic methods that generate challenging tasks for the agent at each iteration to improve generalization on unseen target tasks [Reference Al-Shedivat, Bansal, Burda, Sutskever, Mordatch and Abbeel21]. In refs. [Reference Bousmalis, Irpan and Wohlhart30, Reference Tzeng, Devin and Hoffman31], adversarial techniques are implemented by two networks that evolve by competing with each other. More specifically, the discriminator network is optimized to discriminate the real image data from the simulation data, while the generator network is optimized to generate simulation images that can fool the discriminator. Similarly, in Robust Adversarial Reinforcement Learning (RARL) [Reference Pinto, Davidson, Sukthankar and Gupta32], a separate adversarial network is optimized to destabilize the agent during training. Shioya et al. [Reference Shioya, Iwasawa and Matsuo33] extend RARL by varying the adversary policies. Bansal et al. [Reference Bansal, Pachocki, Sidor, Sutskever and Mordatch20] used uniform distribution sampling to determine the iteration of the adversarial humanoid policy from the subset of recent iterations.
In this paper, we propose regularization techniques to improve the performance of target tasks. We show experimentally that not taking into account the overfitting as well as the different dimensionality of the robots can lead to inaccurate evaluation. For this reason, we first show that performance on the source task is not indicative of generalization ability and performance on the target task. Reliable evaluation of results becomes difficult without regularization, as baselines may underperform.
We propose Strict Clipping PPO (SC-PPO) to discard the samples that lead to overfitting by increasing the lower bound on the policy gradient loss. We apply SC by lowering the clipping parameter in PPO to extremely small values and prove its effect numerically on a high-dimensional humanoid robot and a hopper robot in the MuJoCo environment [Reference Todorov, Erez and Tassa6]. This regularization technique improves the performance of the policy in the target task and provides a competitive benchmark. We evaluate our method in benchmarks presented in refs. [Reference Pinto, Davidson, Sukthankar and Gupta32] and [Reference Henderson, Chang, Shkurti, Hansen, Meger and Dudek34]. We then verify our methods on both novel target tasks involving transfer to robots with different morphologies and target tasks with a wider range of dynamics parameters. These novel tasks include tall, short, and delivery service humanoid target tasks, each with a different center of mass and morphology than the standard humanoid source task.
In transfer RL problems where the environmental dynamics of the target task diverge more from the source task, we apply early stopping. We show that policy trained in the source task starts to overfit the target task after several policy iterations. In this context, earlier iterations of policies perform well in comparative analysis because stopping training earlier prevents overfitting the source task. Hence, we show that recognizing the policy iteration number as a hyperparameter increases the performance of state-of-the-art algorithms such as PPO and RARL [Reference Pinto, Davidson, Sukthankar and Gupta32].
We compare the generalization abilities of different adversarial training methods, namely entropy bonuses, advantage estimation techniques, and different curriculum learning methods with RARL. We integrate an entropy bonus in adversarial RL in Maximum Entropy Robust Adversarial Reinforcement Learning (ME-RARL) to increase domain randomization. We improve generalization using the advantage estimation component by including both value function estimator critic networks at each optimization iteration with Average Consecutive Critic Robust Adversarial Reinforcement Learning (ACC-RARL). We compare RARL and Shared Critic RARL (SC-RARL) [Reference Dong35] with our methods on the torso mass [Reference Pinto, Davidson, Sukthankar and Gupta32] and gravity benchmarks, where the hopper is required to hop without falling. The only difference between SC-RARL and RARL is that in SC-RARL a single critic network is used to approximate the value function. In ref. [Reference Dong35], no regularization is used, so the generalization capacity is similar to RARL. In our work, we first regularize all adversarial architectures and then compare their generalization ability. Table I shows the performance in the target tasks generated by changing the mass of the torso in the range [Reference Gupta, Eppner, Levine and Abbeel1, Reference Li, Cheng, Peng, Abbeel, Levine, Berseth and Sreenath9], and the target tasks generated by changing the gravity of the environment in the range [0.5G, 1.75G]. We use the same source task for training, where the mass of the torso is approximately 3.53 units and the gravity is
![]() $G=9.81$
. Our methods can successfully extrapolate to the generated target tasks outperforming RARL in all benchmarks.
$G=9.81$
. Our methods can successfully extrapolate to the generated target tasks outperforming RARL in all benchmarks.
Table I. Target task extrapolation success range.

In Section 2, studies on the transfer RL and adversarial learning are provided. The proposed methods along with the background will be detailed in Section 3. Experimental setup and results will be given in Sections 4 and 5, respectively. Finally, in Section 6, the conclusion section will include a summary of our contributions, a discussion of the results, and future directions for research.
2. Problem formulation
We address the forward transfer learning problem in the context of learning control. To learn a set of robust, generalizable policies from a single source task we use deep RL. In RL, the iterative decision process of an agent is formulated as a Markov Decision Process (MDP). We characterize the MDPs with the initial state distribution
![]() $\rho (s_0) \,:\, \mathcal{ S } \rightarrow \mathbb{ R }$
, state transition distribution
$\rho (s_0) \,:\, \mathcal{ S } \rightarrow \mathbb{ R }$
, state transition distribution
![]() $ \rho{ (s_{t+1}|s_t,a_t)} \,:\, \mathcal{ S } \times \mathcal{ A } \times \mathcal{ S } \rightarrow \mathbb{ R }$
, reward function
$ \rho{ (s_{t+1}|s_t,a_t)} \,:\, \mathcal{ S } \times \mathcal{ A } \times \mathcal{ S } \rightarrow \mathbb{ R }$
, reward function
![]() $ r_t \,:\, \mathcal{ S } \times \mathcal{ A } \times \mathcal{ S } \rightarrow \mathbb{ R }$
, and discount factor
$ r_t \,:\, \mathcal{ S } \times \mathcal{ A } \times \mathcal{ S } \rightarrow \mathbb{ R }$
, and discount factor
![]() $ \gamma \in ( 0,1 )$
by
$ \gamma \in ( 0,1 )$
by
![]() $ ( \mathcal{ S }, \mathcal{ A },\rho{ (s_{t+1}|s_t,a_t)}, r_t, \rho{ (s_0) }, \gamma )$
.
$ ( \mathcal{ S }, \mathcal{ A },\rho{ (s_{t+1}|s_t,a_t)}, r_t, \rho{ (s_0) }, \gamma )$
.
Kinematic constraints are provided by the simulator. The pertinent kinematic constraints, including the joint limit constraints (range) of each actuated joint, used in the humanoid and hopper environments are provided in Table VII, Appendix A. Detailed information on the constraint model, constraint solver, and kinematics tree of the default humanoid environment can be found in the MuJoCo Documentation [36] and Open AI Gym Toolkit [Reference Brockman, Cheung, Pettersson, Schneider, Schulman, Tang and Zaremba37]. The constraints used in kinetic energy minimization are the friction-cone constraint, given as a hard constraint, and the non-penetration constraint [Reference Todorov, Erez and Tassa6]. Kinetic and kinematic constraints can also be included in the reward function as in ref. [Reference Gangapurwala, Mitchell and Havoutis5]. Our reward function attempts to realize balance constraints by episode termination upon violation of the balance constraint following the RL framework. The termination criterion for bipedal locomotion in humanoids depends on the location of the center of the torso. When the +z location of the center of mass of the robot is below a threshold, the robot is presumed to fall and the episode is terminated.
Our purpose is to improve the generalization of the state-of-the-art policy optimization methods in model-free RL where the policy is represented as a neural network. In model-free RL, a policy is optimized directly without learning the complex state transition dynamics. To evaluate the generalizability of these policies, we design a wide range of target control tasks inspired by real-world scenarios. In particular, we use hopper tasks to compare our methods to RARL [Reference Pinto, Davidson, Sukthankar and Gupta32] and humanoid tasks to compare our methods to PPO [Reference Schulman, Wolski, Dhariwal, Radford and Klimov17].
Similar to the hopper benchmark in ref. [Reference Rajeswaran, Ghotra, Ravindran and Levine38], we change the tangential friction coefficient of the ground to generate a target task for the humanoid. Our goal is to transfer the learning experience from a source task with a ground tangential friction coefficient of 1 to a target task with a ground tangential friction coefficient of 3.5. Transferring among morphologically different robots with different limb sizes or torso masses has been a popular multi-task learning benchmark [Reference Pinto, Davidson, Sukthankar and Gupta32, Reference Henderson, Chang, Shkurti, Hansen, Meger and Dudek34, Reference Rajeswaran, Ghotra, Ravindran and Levine38]. Accordingly, we generate three novel target environments: a taller and heavier humanoid robot, a shorter and lighter humanoid robot, and a delivery humanoid robot that carries a heavy box.
Similar to the multi-task transfer learning experiments in ref. [Reference Henderson, Chang, Shkurti, Hansen, Meger and Dudek34], we generate target tasks by altering the torso mass of the robot and the gravity of the environment. In ref. [Reference Henderson, Chang, Bacon, Meger, Pineau and Precup39], 4 target tasks were created by changing the gravity parameters of the environment in the range [0.50G, 1.50G] where G = −9.81. In our experiments, we use a larger range [0.50G, 1.75G] to discover the range of tasks our method can solve. Similarly, for the torso mass experiments, we create target tasks by significantly increasing the range of the torso mass of the robot to [1.0, 9.0] from the range [2.75, 4.5] used in RARL.
3. Background
Before providing the details of our components, we will explain the adversarial and deep reinforcement algorithms. We build our method on top of RARL algorithm which is characterized as a two-player zero-sum discounted game. The return of the agent is formalized as follows [Reference Pinto, Davidson, Sukthankar and Gupta32].
 \begin{equation} \begin{aligned} R ^{ 1 } &= E _{ s _{ 0 } \sim \rho, a ^{ 1 } \sim \mu ( s ), a ^{ 2 } \sim \nu ( s ) } \left [ \sum _{ t = 0 } ^{ T - 1 } r^{ 1 } \!\left( s_t, a_t ^{ 1 }, a_t ^{ 2 } \right ) \right ] \end{aligned} \end{equation}
\begin{equation} \begin{aligned} R ^{ 1 } &= E _{ s _{ 0 } \sim \rho, a ^{ 1 } \sim \mu ( s ), a ^{ 2 } \sim \nu ( s ) } \left [ \sum _{ t = 0 } ^{ T - 1 } r^{ 1 } \!\left( s_t, a_t ^{ 1 }, a_t ^{ 2 } \right ) \right ] \end{aligned} \end{equation}
Actions
![]() $a^1$
are sampled from the policy
$a^1$
are sampled from the policy
![]() $\mu$
of the agent and actions
$\mu$
of the agent and actions
![]() $a^2$
are sampled from the policy
$a^2$
are sampled from the policy
![]() $\nu$
of the adversary.
$\nu$
of the adversary.
![]() $s _{ 0 }$
is the initial state sampled from the initial state distribution
$s _{ 0 }$
is the initial state sampled from the initial state distribution
![]() $ \rho$
.
$ \rho$
.
![]() $s_t$
is the state at timestep t, and r corresponds to the reward function. The agent maximizes its return whereas the adversary minimizes the return of the agent. Thus, the return of the adversary is
$s_t$
is the state at timestep t, and r corresponds to the reward function. The agent maximizes its return whereas the adversary minimizes the return of the agent. Thus, the return of the adversary is
![]() $R ^{ 2 }=-R ^{ 1 }$
[Reference Pinto, Davidson, Sukthankar and Gupta32].
$R ^{ 2 }=-R ^{ 1 }$
[Reference Pinto, Davidson, Sukthankar and Gupta32].
We use PPO to update actor-critic networks of the agent and the adversary in RARL experiments. Actor network determines the actions the agent takes, whereas the critic network estimates the value function used for the advantage function estimation. Advantage function estimates how rewarding it is to take the action in the state compared to the value of that state. We use a particular loss function, namely Clipped PPO Loss,
![]() $L ^{ C L I P }$
[Reference Schulman, Wolski, Dhariwal, Radford and Klimov17] that optimizes the parameters
$L ^{ C L I P }$
[Reference Schulman, Wolski, Dhariwal, Radford and Klimov17] that optimizes the parameters
![]() $\theta$
of the actor policy network as follows.
$\theta$
of the actor policy network as follows.
Generalized Advantage Estimator (GAE) [Reference Schulman, Moritz, Levine, Jordan and Abbeel40]
![]() $\hat{ A } _{ t }$
is used to optimize the actor network. If the advantage
$\hat{ A } _{ t }$
is used to optimize the actor network. If the advantage
![]() $\hat{ A } _{ t }$
is negative then the probability ratios below
$\hat{ A } _{ t }$
is negative then the probability ratios below
![]() $1 - \varepsilon$
are clipped and if the advantage is positive, then the probability ratios above
$1 - \varepsilon$
are clipped and if the advantage is positive, then the probability ratios above
![]() $1 + \varepsilon$
are clipped. Gradient flow does not occur, and the samples are discarded if the probability ratio
$1 + \varepsilon$
are clipped. Gradient flow does not occur, and the samples are discarded if the probability ratio
![]() $\dfrac{\pi _{\theta }\!\left(a_{t} \mid s_{t}\right )}{\pi _{\theta _{\text{old }}}\!\left(a_{t} \mid s_{t}\right )}$
is clipped and the expression
$\dfrac{\pi _{\theta }\!\left(a_{t} \mid s_{t}\right )}{\pi _{\theta _{\text{old }}}\!\left(a_{t} \mid s_{t}\right )}$
is clipped and the expression
![]() $\left (\operatorname{ clip } \!\left(\dfrac{\pi _{\theta }\!\left(a_{t} \mid s_{t}\right )}{\pi _{\theta _{\text{old }}}\!\left(a_{t} \mid s_{t}\right )}, 1 - \varepsilon, 1 + \varepsilon \right ) \hat{ A } _{ t } \right )$
is minimum.
$\left (\operatorname{ clip } \!\left(\dfrac{\pi _{\theta }\!\left(a_{t} \mid s_{t}\right )}{\pi _{\theta _{\text{old }}}\!\left(a_{t} \mid s_{t}\right )}, 1 - \varepsilon, 1 + \varepsilon \right ) \hat{ A } _{ t } \right )$
is minimum.
![]() $\pi _{\theta }\!\left(a_{t} \mid s_{t}\right )$
is the current policy being optimized whereas
$\pi _{\theta }\!\left(a_{t} \mid s_{t}\right )$
is the current policy being optimized whereas
![]() $\pi _{\theta _{\text{old }}}\!\left(a_{t} \mid s_{t}\right )$
is the previous policy.
$\pi _{\theta _{\text{old }}}\!\left(a_{t} \mid s_{t}\right )$
is the previous policy.
![]() $\varepsilon$
is the clipping parameter that controls the lower bound on the Clipped PPO Loss. Open AI Baselines framework and most of the literature has been using the clipping parameter of 0.2 for continuous control tasks [Reference Schulman, Wolski, Dhariwal, Radford and Klimov17, Reference Bansal, Pachocki, Sidor, Sutskever and Mordatch20, Reference Al-Shedivat, Bansal, Burda, Sutskever, Mordatch and Abbeel21, Reference Huang, Gu, Wu and Guan22, Reference Dhariwal, Hesse and Klimov41, Reference Henderson, Islam, Bachman, Pineau, Precup and Meger42].
$\varepsilon$
is the clipping parameter that controls the lower bound on the Clipped PPO Loss. Open AI Baselines framework and most of the literature has been using the clipping parameter of 0.2 for continuous control tasks [Reference Schulman, Wolski, Dhariwal, Radford and Klimov17, Reference Bansal, Pachocki, Sidor, Sutskever and Mordatch20, Reference Al-Shedivat, Bansal, Burda, Sutskever, Mordatch and Abbeel21, Reference Huang, Gu, Wu and Guan22, Reference Dhariwal, Hesse and Klimov41, Reference Henderson, Islam, Bachman, Pineau, Precup and Meger42].
4. Method
The proposed regularization framework for obtaining generalizable policies is outlined in Fig. 1. The protagonist controls the actuators of the robot. Actor-critic models are trained using trajectories collected from the source task. The trajectory data consist of states, actions, next states, and rewards. During the training of the protagonist (I), the policy parameters are stored in the policy buffer (III) to be used in the generated unseen target environments (IV). Section 4.1 describes the policy buffer used to obtain generalizable policies for transfer. For strict clipping (SC), only the protagonist actor-critic model is trained (I) on the source task environment using the SC parameter
![]() $\varepsilon$
. Section 4.2 provides the component SC, which prevents policy updates when training samples improve the source task objective above a threshold. A low threshold stabilizes the training and regularizes the source task loss function.
$\varepsilon$
. Section 4.2 provides the component SC, which prevents policy updates when training samples improve the source task objective above a threshold. A low threshold stabilizes the training and regularizes the source task loss function.

Figure 1. Proposed architecture and procedures for transfer RL.
The protagonist (I) is trained with the adversary (II). The adversary controls the 3-dimensional destabilizing forces acting on the robot’s body segment. The critic models are initialized and trained separately in all adversarial techniques following the representation in the diagram, except for the shared critic method.
![]() $\beta _{pro}$
,
$\beta _{pro}$
,
![]() $a_{protagonist}$
,
$a_{protagonist}$
,
![]() $r_{protagonist}$
, and
$r_{protagonist}$
, and
![]() $\beta _{adv}$
,
$\beta _{adv}$
,
![]() $a_{adversary}$
,
$a_{adversary}$
,
![]() $r_{adversary}$
are the model-specific entropy parameters, actions, and rewards of the protagonist and adversary actor models, respectively. More precisely, the entropy parameters control the stochasticity of the corresponding actions. Details on how the agent is encouraged to explore the environment, how different deep RL architectures are used, and how incremental learning is employed to avoid overfitting are discussed in Section 4.3.
$r_{adversary}$
are the model-specific entropy parameters, actions, and rewards of the protagonist and adversary actor models, respectively. More precisely, the entropy parameters control the stochasticity of the corresponding actions. Details on how the agent is encouraged to explore the environment, how different deep RL architectures are used, and how incremental learning is employed to avoid overfitting are discussed in Section 4.3.
4.1. Policy buffer
Policies trained with different hyperparameters show different control patterns. We propose a policy buffer to store these policies that are trained with the same loss function but with different hyperparameters. We add the iteration number to the hyperparameter set for transfer RL benchmarks. In simulated experiments, we show that it is possible to extract a comprehensive set of policies capable of exhibiting various skills from a single source task.
Our method is inspired by the early stopping regularization technique that is frequently used in supervised learning. Similar to supervised learning, in the transfer RL setting, snapshots of policy parameters taken at different steps have different performances in the target task. We train policies with different hyperparameters and take snapshots of the corresponding policies at each optimization iteration at predetermined intervals and save them in the policy buffer. Previous works trained single policies for a constant number of iterations in the source task. In contrast, we evaluate multiple policies from the buffer to determine the iteration number where the model starts to overfit.
Our aim here is to generate successful policies for a range of target tasks that are represented by task parameters such as gravity, friction, mass, and center of mass of the robot. Overfitting is predominant in cases where the target tasks deviate significantly from the source task. Inspired by the validation dataset idea used in early stopping regularization for supervised learning, we propose designing a proxy validation tasks set. Given source and target task parameters and the policies learned in the source task, we form proxy validation tasks between source and target tasks with parameters closer to the target task. Expected rewards of the policies trained with different hyperparameters are informative in finding the generalizable policies from the buffer.
4.2. Strict clipping
To train the aforementioned policies, we use policy gradient algorithms. In literature, hyperparameter tuning of the RL component is commonly overlooked and a fixed set of hyperparameters is used when integrating the RL component into the transfer domain.
Gradient clipping in Eq. (2) is generally used to discourage catastrophic displacement in the parameter space. In our work, we additionally propose that it can be used for regularization in transfer RL. In particular, we propose a new regularization technique for PPO, namely SC to avoid overfitting by constraining the gradient updates. During training, SC-PPO allows more source task samples to be discarded which would otherwise lead to overfitting. SC-PPO is used to further decrease the gradient movement in the policy parameter space in favor of generalization. This is achieved by decreasing the clipping parameter used in PPO by one or less order of magnitude. We prove that this method is superior to the unregularized RARL baseline in multiple transfer learning benchmarks.
4.3. Regularization in adversarial reinforcement learning
Introducing an adversary to destabilize the agent using multidimensional simulated forces has generated successful results in continuous control tasks in RARL. However, we experimentally prove that unregularized RARL performs worse than regularized PPO. In contrast to prior work, we acknowledge policy iteration as a hyperparameter in all our comparisons. Thus, we compare our methods in an adversarial framework by forming a policy buffer and extracting the most generalizable policies to increase the robustness of the algorithm. More specifically, we regularized critic networks, increased exploration, and integrated curriculum learning in an adversarial RL framework.
4.3.1. Average consecutive critic robust adversarial reinforcement learning (ACC-RARL) (I)
Similar to actor networks, critic networks are function approximators that are prone to overfitting. We propose ACC-RARL, which computes advantage estimates using the mean of the critic outputs. Critics are optimized with their actor pair consecutively. We aim to decrease overfitting by using double critic networks with different random initializations and reuse the previous model by including the output of the previously updated critic in the advantage estimation. The temporal difference residual of the approximate value function with discount
![]() $\gamma$
at timestep
$\gamma$
at timestep
![]() $t$
corresponds to
$t$
corresponds to
![]() $\delta _{ t }$
. The temporal difference residuals of the protagonist and the adversary in ACC-RARL are shown as follows.
$\delta _{ t }$
. The temporal difference residuals of the protagonist and the adversary in ACC-RARL are shown as follows.
where
![]() $V_{adv}$
,
$V_{adv}$
,
![]() $V_{pro}$
correspond to the critic network of the adversary, and the critic network of the protagonist respectively.
$V_{pro}$
correspond to the critic network of the adversary, and the critic network of the protagonist respectively.
4.3.2. Maximum entropy robust adversarial reinforcement learning (II)
Entropy bonus is used for exploration by rewarding the variance in the distribution of the action probabilities. We incorporate an entropy bonus
![]() $H[\pi ^{pro}]$
for the protagonist and an entropy bonus
$H[\pi ^{pro}]$
for the protagonist and an entropy bonus
![]() $H\left[\pi ^{adv}\right]$
for the adversary in the reward functions. Updated reward functions of the adversary
$H\left[\pi ^{adv}\right]$
for the adversary in the reward functions. Updated reward functions of the adversary
![]() $R_{t}\!\left(\pi ^{adv}_{\theta }\right)$
and the protagonist
$R_{t}\!\left(\pi ^{adv}_{\theta }\right)$
and the protagonist
![]() $R_{t}\!\left(\pi ^{pro}_{\theta }\right)$
are given
$R_{t}\!\left(\pi ^{pro}_{\theta }\right)$
are given
 \begin{equation} \begin{aligned} R_{t}\!\left(\pi ^{adv}_{\theta }\right)&= \hat{ \mathbb{ E } } _{ t }\left[ R_{t}^{actor}\!\left(\pi ^{adv}_{\theta }\right) - R_{t}^{critic}\!\left(\pi ^{adv}_{\theta }\right) + \beta _{adv}{H\left[\pi ^{adv}\right]{\theta }(s_t)}\right]\\
R_{t}\!\left(\pi ^{pro}_{\theta }\right)&= \hat{ \mathbb{ E } } _{ t }\left[ R_{t}^{actor}\!\left(\pi ^{pro}_{\theta }\right) - R_{t}^{critic}\!\left(\pi ^{pro}_{\theta }\right) + \beta _{pro}{H\left[\pi ^{pro}\right]{\theta }(s_t)}\right] \end{aligned} \end{equation}
\begin{equation} \begin{aligned} R_{t}\!\left(\pi ^{adv}_{\theta }\right)&= \hat{ \mathbb{ E } } _{ t }\left[ R_{t}^{actor}\!\left(\pi ^{adv}_{\theta }\right) - R_{t}^{critic}\!\left(\pi ^{adv}_{\theta }\right) + \beta _{adv}{H\left[\pi ^{adv}\right]{\theta }(s_t)}\right]\\
R_{t}\!\left(\pi ^{pro}_{\theta }\right)&= \hat{ \mathbb{ E } } _{ t }\left[ R_{t}^{actor}\!\left(\pi ^{pro}_{\theta }\right) - R_{t}^{critic}\!\left(\pi ^{pro}_{\theta }\right) + \beta _{pro}{H\left[\pi ^{pro}\right]{\theta }(s_t)}\right] \end{aligned} \end{equation}
where
![]() $\pi ^{adv}_{\theta }$
,
$\pi ^{adv}_{\theta }$
,
![]() $\pi ^{pro}_{\theta }$
, and
$\pi ^{pro}_{\theta }$
, and
![]() $\beta$
correspond to the policy of the adversary, policy of the protagonist, and the entropy coefficient respectively. Increasing exploration at the cost of decreasing source task performance increases the generalization capacity of the algorithm. However, we acknowledge that adjusting the stochasticity of the environment while avoiding detrimental impact on learning is challenging. Adding an entropy bonus to the loss function of the adversary increases the domain randomization, affecting the performance of both the protagonist and the adversary. We compare the ME-RARL algorithms: entropy regularized RARL (ERARL) and entropy regularized ACC-RARL (EACC-RARL) in more challenging hopper morphology and gravity benchmarks where SC-PPO is not sufficient.
$\beta$
correspond to the policy of the adversary, policy of the protagonist, and the entropy coefficient respectively. Increasing exploration at the cost of decreasing source task performance increases the generalization capacity of the algorithm. However, we acknowledge that adjusting the stochasticity of the environment while avoiding detrimental impact on learning is challenging. Adding an entropy bonus to the loss function of the adversary increases the domain randomization, affecting the performance of both the protagonist and the adversary. We compare the ME-RARL algorithms: entropy regularized RARL (ERARL) and entropy regularized ACC-RARL (EACC-RARL) in more challenging hopper morphology and gravity benchmarks where SC-PPO is not sufficient.
4.3.3. Curriculum learning (III)
Curriculum learning focuses on discovering the optimal arrangement of the source tasks to perform better on the target task. We utilize curriculum learning by randomizing the adversary policy iterations from different sets of advancement. We compare the target task performance of protagonist policies trained with adversaries randomly chosen from the last predefined number of iterations. We use
![]() $\chi$
to denote the fraction of the latest iterations of adversaries recorded up to the current iteration. Adversaries loaded from and recorded to the buffer during curriculum training become less capable and more inconsistent as the training progress and
$\chi$
to denote the fraction of the latest iterations of adversaries recorded up to the current iteration. Adversaries loaded from and recorded to the buffer during curriculum training become less capable and more inconsistent as the training progress and
![]() $\chi$
decreases. In consequence, we intend to show how a variety of design decisions during training affects the target task performance in the pursuit of developing novel regularization techniques and more reliable benchmarks.
$\chi$
decreases. In consequence, we intend to show how a variety of design decisions during training affects the target task performance in the pursuit of developing novel regularization techniques and more reliable benchmarks.
5. Results
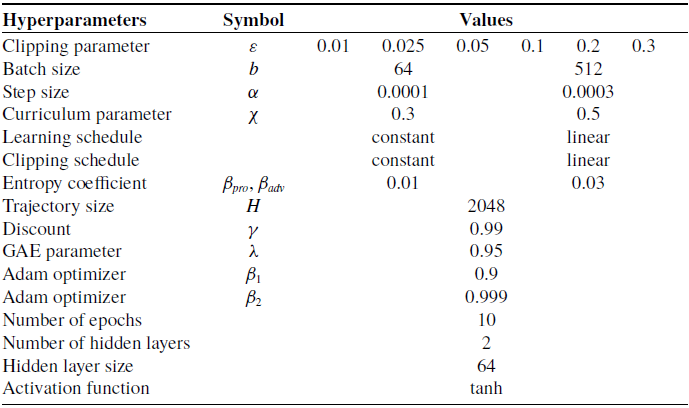
After detailing source task training implementations in Sections 5.1 and 5.2, we provide results of our methods SC-PPO in Section 5.3 and ACC-RARL, maximum entropy RARL in Section 5.4 using various target tasks. The hyperparameters used in source task training are given in Table IX, Appendix B. We report on the expected mean and standard deviation of the rewards obtained from 32 randomly seeded identical environments for each target task.
5.1. Humanoid environment
The policy network trained for the 24-DoF humanoid task takes a 376-dimensional state vector as input and outputs the mean vector of a diagonal multivariate Gaussian distribution. An action corresponding to a 17-dimensional torque command is sampled from the corresponding output distribution. At each timestep, the MuJoCo physics simulator executes the torque commands and the result of the execution is used to generate the 376-dimensional next state vector. The reward function of the humanoid environment and the episode termination conditions, including the balance constraint, are provided in Figs. 16 and 17, Appendix C. The average reward per episode and standard deviations of the policies trained with 4 different sets of hyperparameters are shown in Fig. 2(b).

Figure 2. (a) Humanoid running in the source environment. (b) Learning curves of SC-PPO and PPO on standard humanoid source task.
The learning curves obtained using SC in the source tasks are shown in Fig. 2(b) with clipping hyperparameters 0.01, 0.025, and 0.01 decaying learning rate and clipping. The default clipping parameters are 0.01 for SC-PPO, and 0.1 for PPO in all humanoid experiments, unless explicitly specified. Learning curve obtained with the hyperparameters suggested in OpenAI Baselines for the Humanoid environment are represented by the red curve.
5.2. Hopper environment
Hopper environments are used to compare regularized adversarial methods with RARL. The reward function of the Hopper environment is provided in Appendix D. SC-PPO was trained using
![]() $\alpha =0.0003$
,
$\alpha =0.0003$
,
![]() $\epsilon =0.05$
,
$\epsilon =0.05$
,
![]() $b=2048$
, and the adversarial algorithms were trained with
$b=2048$
, and the adversarial algorithms were trained with
![]() $\alpha =0.0003$
,
$\alpha =0.0003$
,
![]() $\epsilon =0.3$
,
$\epsilon =0.3$
,
![]() $b=512$
. Source task learning curves of PPO and RARL trained with different critic architectures are shown in Fig. 3(b).
$b=512$
. Source task learning curves of PPO and RARL trained with different critic architectures are shown in Fig. 3(b).

Figure 3. (a) Hopping action, and (b) learning curves of ACC-RARL, SC-RARL, RARL, SC-PPO on standard hopper source task.
Results in hopper tasks are consistent with the humanoid experiments. To analyze the effect of different architectures on the generalization capacity, we compare three different critic architectures: separate double critic networks used in RARL, single critic network in Shared Critic Robust Adversarial Reinforcement Learning (SC-RARL) and ACC-RARL. The policies trained with different variations of RARL perform similar to SC-PPO in hopper morphology tasks in the range of 1–6 and hopper gravity tasks in the range of 1G–1.5G.
5.3. Regularization via PPO hyperparameter tuning
5.3.1. The morphology experiments
The morphological target tasks are created for inter-robot transfer learning. The short, tall, and delivery humanoid target tasks in Figs. 4(b), (c), (d) are generated from the standard humanoid source task in Fig. 4(a).
The total body weights of the short and tall humanoid target tasks differ from the humanoid source task by the exclusion and inclusion of the upper waist respectively. The tall humanoid task is more challenging than the short humanoid task because it is harder to balance heavier upper body mass where the center of mass is higher from the ground. The threshold for termination is higher for the tall humanoid and lower for the short humanoid because of the different locations of the center of mass.
Table II. Delivery humanoid environment.

Masses of the relevant body parts for the delivery humanoid are given in Table II. Considering the total body mass of 40, a box with a unit mass of 5 constitutes a challenging benchmark. Our purpose is to create a horizontal imbalance by enforcing the humanoid to carry the box only by the right hand.
The comparison of the target task performances of policies trained with clipping parameters
![]() $\epsilon =0.1$
and
$\epsilon =0.1$
and
![]() $\epsilon =0.01$
is provided in Fig. 5(a), (b) and (c). High average reward per episode obtained after
$\epsilon =0.01$
is provided in Fig. 5(a), (b) and (c). High average reward per episode obtained after
![]() $1200^{th}$
iteration with SC-PPO
$1200^{th}$
iteration with SC-PPO
![]() $\epsilon =0.01$
shows that humanoid learns transferable general characteristics of forward locomotion from the source task. In contrast, all iterations of the policies trained with clipping parameter
$\epsilon =0.01$
shows that humanoid learns transferable general characteristics of forward locomotion from the source task. In contrast, all iterations of the policies trained with clipping parameter
![]() $\epsilon =0.1$
failed in all target tasks. Early stopping regularization technique alone is not sufficient because the short and tall humanoids cannot stand still using the earlier iterations of the policy trained with clipping parameter
$\epsilon =0.1$
failed in all target tasks. Early stopping regularization technique alone is not sufficient because the short and tall humanoids cannot stand still using the earlier iterations of the policy trained with clipping parameter
![]() $\epsilon =0.1$
.
$\epsilon =0.1$
.

Figure 4. (a) Standard humanoid source task with 3 torso components, (b) short humanoid target task with 2 torso components, (c) tall humanoid target task with 4 torso components, and (d) delivery humanoid target task.
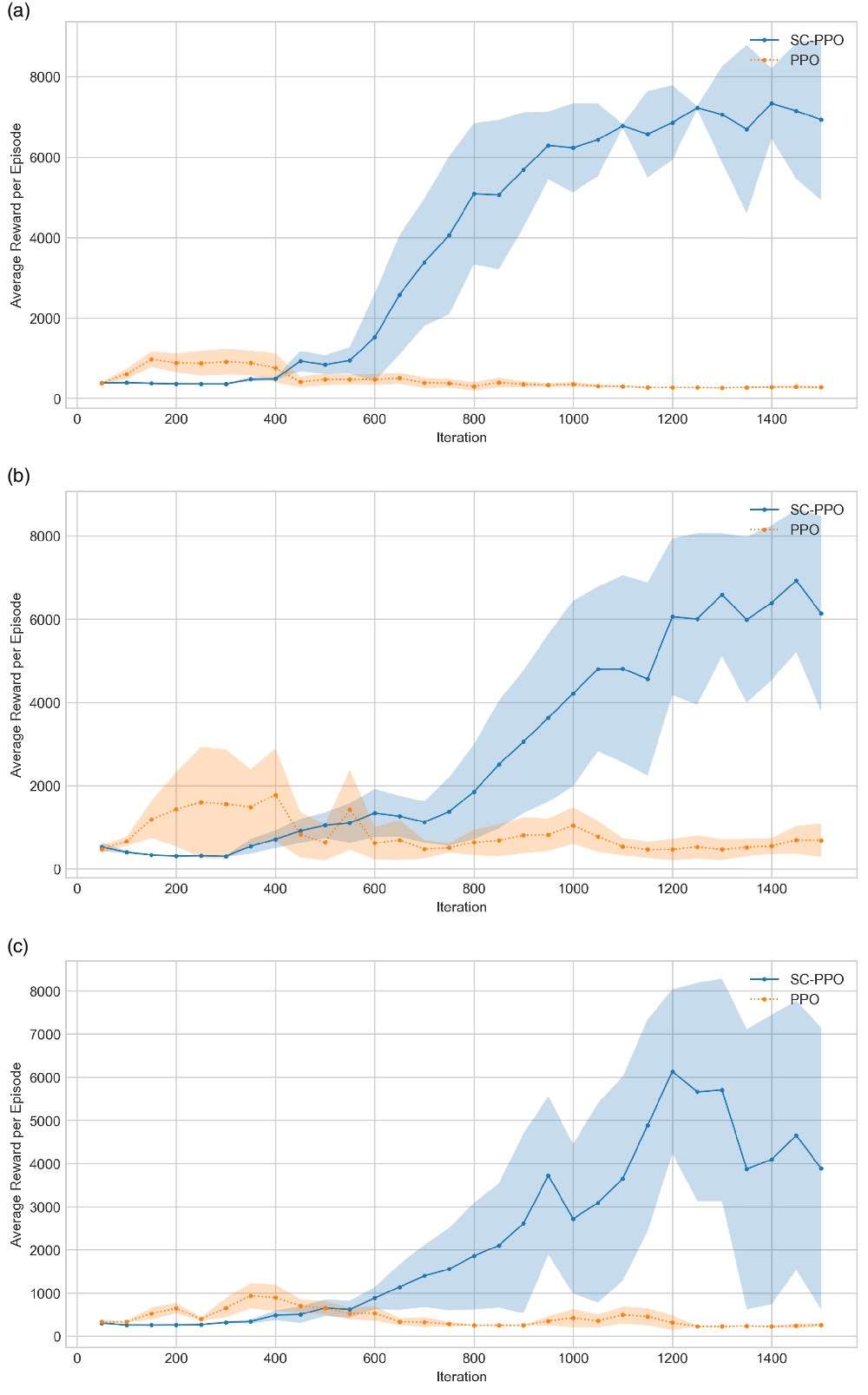
Figure 5. Performance of SC-PPO and PPO on (a) shorter and lighter humanoid target task, (b) taller and heavier humanoid target task, and (c) delivery humanoid target task.
The reduction in the performance after the
![]() $1200^{th}$
iteration in Fig. 5(c) supports the method of resorting to the earlier policy iterations. This concavity suggests that overfitting occurs and early stopping is an effective regularization technique.
$1200^{th}$
iteration in Fig. 5(c) supports the method of resorting to the earlier policy iterations. This concavity suggests that overfitting occurs and early stopping is an effective regularization technique.
The same policy iteration (
![]() $1200^{th}$
) trained with SC-PPO can be successfully transferred to short, tall, and delivery humanoid tasks as shown in Fig. 5(a), (b) and (c). Evaluation of the best source task policies in the target tasks assesses our claim that source task performance is not indicative of the generalization capacity. Thus, all transfer RL methods should account for regularization first.
$1200^{th}$
) trained with SC-PPO can be successfully transferred to short, tall, and delivery humanoid tasks as shown in Fig. 5(a), (b) and (c). Evaluation of the best source task policies in the target tasks assesses our claim that source task performance is not indicative of the generalization capacity. Thus, all transfer RL methods should account for regularization first.
5.3.2. The friction environment
Our aim in this experiment is to evaluate our methods in transfer learning benchmarks where the environment dynamics are changed. We generate a target task by increasing the ground friction coefficient in MuJoCo environment. The humanoid sinks due to high tangential friction but can still run following the regularized policies trained with SC-PPO.
The best jumpstart performances for each clipping parameter are given in Fig. 6. For instance, the last iteration of the policy with a SC-PPO parameter
![]() $\epsilon =0.01$
has an average target task reward of 8283 with 24.3 standard deviation as provided in Table III. In contrast, the best-performing policy in the source task has a target task performance which assesses our claim that source task performance on transfer RL is not indicative of the target task performance. These results show that agent trained using our methods learns generalizable skills for environments with changing dynamics.
$\epsilon =0.01$
has an average target task reward of 8283 with 24.3 standard deviation as provided in Table III. In contrast, the best-performing policy in the source task has a target task performance which assesses our claim that source task performance on transfer RL is not indicative of the target task performance. These results show that agent trained using our methods learns generalizable skills for environments with changing dynamics.
Table III. Comparison of SC-PPO and PPO in target friction environment.


Figure 6. Performance of SC-PPO and PPO on target environment with tangential friction 3.5 times the source environment.
5.3.3. The gravity environments
Our aim in these experiments is to evaluate our methods in a different set of target tasks where environment parameters are changed. Similar to the friction experiments, we generate gravity target tasks in the range of 0.5G–1.75G where G = −9.81 is the gravity of the source task.
When the last iteration of the policy trained with SC-PPO
![]() $\epsilon =0.025$
is used in the target task with gravity = −4.905 (
$\epsilon =0.025$
is used in the target task with gravity = −4.905 (
![]() $0.5G_{Earth}$
), the humanoid in Fig. 7(a) can run. Performance of SC-PPO is slightly better than early stopping for this target task. Similarly, in the target task with gravity = −14.715 (
$0.5G_{Earth}$
), the humanoid in Fig. 7(a) can run. Performance of SC-PPO is slightly better than early stopping for this target task. Similarly, in the target task with gravity = −14.715 (
![]() $1.5G_{Earth}$
), the humanoid needs to resort to the previous snapshots of the policy trained with SC-PPO
$1.5G_{Earth}$
), the humanoid needs to resort to the previous snapshots of the policy trained with SC-PPO
![]() $\epsilon =0.025$
as plotted in the Fig. 8(a). The bipedal locomotion pattern in the simulated target environment with gravity = −14.715 (
$\epsilon =0.025$
as plotted in the Fig. 8(a). The bipedal locomotion pattern in the simulated target environment with gravity = −14.715 (
![]() $1.5G_{Earth}$
) when the humanoid jumpstarts with the
$1.5G_{Earth}$
) when the humanoid jumpstarts with the
![]() $600^{th}$
policy trained with clipping parameter
$600^{th}$
policy trained with clipping parameter
![]() $\epsilon =0.025$
is shown in Fig. 8(b).
$\epsilon =0.025$
is shown in Fig. 8(b).

Figure 7. Performance of SC-PPO and PPO on target environment with gravity = −4.905 (
![]() $0.5G_{Earth}$
).
$0.5G_{Earth}$
).

Figure 8. Performance of SC-PPO and PPO on target environment with gravity = −14.715 (
![]() $0.5G_{Earth}$
).
$0.5G_{Earth}$
).
Gravity benchmarks for the humanoid indicate that snapshots of different policies should be used for the target task with gravity = −17.1675 (
![]() $1.75G_{Earth}$
). The policy iterations trained with hyperparameters “
$1.75G_{Earth}$
). The policy iterations trained with hyperparameters “
![]() $\epsilon =0.01$
decaying learning rate and clipping” performed poorly in the source task and target task with lower gravity. However, they perform consistently well in environments with a higher magnitude of gravity (−17.1675, −14.715). Figures 8 and 9 show that decaying the clipping parameter and the learning rate during training decreased the exploration and restricted the humanoid to stick to a more careful way of moving forward after 1000 training iterations.
$\epsilon =0.01$
decaying learning rate and clipping” performed poorly in the source task and target task with lower gravity. However, they perform consistently well in environments with a higher magnitude of gravity (−17.1675, −14.715). Figures 8 and 9 show that decaying the clipping parameter and the learning rate during training decreased the exploration and restricted the humanoid to stick to a more careful way of moving forward after 1000 training iterations.
5.4. Regularization in adversarial reinforcement learning
5.4.1. The morphology experiments
In this set of experiments, we compare our methods with RARL. In RARL, target tasks are generated by modifying the torso mass of the robot in the range of 2.5–4.75. Following the same procedure, we modify the torso mass in the range of 1–9. Table IV provides additional information on the morphology of the Hopper source task.
Table IV. Hopper source environment.


Figure 9. Performance of SC-PPO and PPO on target environment with gravity = −17.1675 (
![]() $1.75G_{Earth}$
).
$1.75G_{Earth}$
).
The robot can successfully generalize using any regularized adversarial technique or SC-PPO with early stopping when the target tasks are in the range of 1-6. Based on the target task performances of ACC-RARL, SC-RARL, and RARL, in Fig. 10, different critic value function approximation techniques have an effect on the type of control behavior learned. However, the performance of some policy iterations trained with RARL, ACC-RARL, SC-RARL starts to become unstable in Fig. 10(a) and (e). In harder target tasks like these, the agent should first resort to earlier snapshots of the policy and use early stopping for adversarial RL. Let us assume that the agent only has several snapshots of the policy in its buffer trained in the source task with standard torso mass. Then, the agent is put in a target task with torso mass = 6 which is analogous to an agent expected to carry weight while performing a control task. We propose that in cases like these, instead of training from the very beginning, the agent should primarily resort to earlier policy iterations because the generalizable policies performing at the expert level are readily available in the agent’s memory and were extracted from the source task training.

Figure 10. Performance of SC-PPO and adversarial methods on Hopper target tasks with torso mass (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, (f) 6, (g) 7.
If we had not recognized the policy iteration as a hyperparameter then comparing the algorithms at arbitrarily selected number of training iterations would not constitute a fair comparison. More importantly, the performance of PPO without adversaries, generally used as a benchmark algorithm, is highly dependent on the number training iterations. Hence for target tasks with torso masses
![]() $[1-6]$
, the right snapshots of SC-PPO are capable of obtaining high average reward per episode as seen in Fig. 10(a), (b), (c), (d), (e), (f). Furthermore, the skills learned with RARL in the last 150 iterations are successful in the source task and target task where torso mass is 3 and 4 units as provided in Fig. 10(c). However, they are clearly unstable in tasks where torso mass is 1, 2, 5, 6, 7 as illustrated in Fig. 10(a). The policy buffer allows us to do a fair comparison among different methods. Training the algorithms for an arbitrary number of iterations will produce inaccurate results such as underperforming baselines or proposed algorithms. Furthermore, the reproducibility of the transfer RL algorithms will be affected.
$[1-6]$
, the right snapshots of SC-PPO are capable of obtaining high average reward per episode as seen in Fig. 10(a), (b), (c), (d), (e), (f). Furthermore, the skills learned with RARL in the last 150 iterations are successful in the source task and target task where torso mass is 3 and 4 units as provided in Fig. 10(c). However, they are clearly unstable in tasks where torso mass is 1, 2, 5, 6, 7 as illustrated in Fig. 10(a). The policy buffer allows us to do a fair comparison among different methods. Training the algorithms for an arbitrary number of iterations will produce inaccurate results such as underperforming baselines or proposed algorithms. Furthermore, the reproducibility of the transfer RL algorithms will be affected.
Regarding the parametric form of target tasks, the performance of the policies residing in the policy buffer can be anticipated. Coinciding with the performances seen in Fig. 10(a), (f), (g), (b), it is anticipated that the earlier policy iterations trained with less samples perform better as the distance between the target task and the source task increases in the task parameter space. We reproduced the original RARL experiment; hence, the results are consistent with the performance of the last policy iteration trained with RARL (Fig. 10(b), (c), (d)).
When the torso mass is increased to 6, significant target performance drop (Fig. 10(f)) occurs until the last policy iteration where all policies are affected. This implies overfitting occurs and policy iterations trained with SC-PPO can still perform optimally around 395. The best-performing policy iterations of adversarial algorithms start to get accumulated in the range
![]() $[150,300]$
when torso mass is greater than 5; thus, a mapping between the target task parameters and the policy iterations is highly probable.
$[150,300]$
when torso mass is greater than 5; thus, a mapping between the target task parameters and the policy iterations is highly probable.
In a harder environment with a torso mass of 7, the earlier iterations of the policy trained with ACC-RARL perform the best. Figure 10(g) shows that the range of the best-performing policy iterations is contracted more.
Using ME-RARL algorithms (EACC-RARL, ESC-RARL, and ERARL) increased the fluctuation of the average rewards for all algorithms as provided in Fig. 11. Because entropy bonus encourages exploration, the adversary takes more randomized actions which often change the protagonist’s hopping behavior. None of the adversarial techniques were successful in completing target tasks without entropy regularization where the torso mass of the hopper is increased to 8 and 9 units. EACC-RARL shows the highest performance on the 9 unit torso mass target task (Fig. 12(b)). The average reward per episode of the policy iterations trained with EACC-RARL is provided in Table VI. These results show that earlier policy iterations show better performance as the target task becomes more challenging. Any target task from the set can be used as a proxy validation task for the tasks that belong to the same set.
First, using SC-PPO and early stopping we formulate a more competitive baseline for the adversarial algorithms. Then, we show the performance of one policy iteration (
![]() $175^{th}$
) with high generalization capacity trained with the ACC-RARL algorithm in Table V to demonstrate that a policy is capable of performing forward locomotion when torso mass is in the range of 1–7. Plots of the torque commands generated by the
$175^{th}$
) with high generalization capacity trained with the ACC-RARL algorithm in Table V to demonstrate that a policy is capable of performing forward locomotion when torso mass is in the range of 1–7. Plots of the torque commands generated by the
![]() $175^{th}$
policy network in the source task and the target task with torso mass 1 are provided in Appendix E. Finally, using EACC-RARL and early stopping we have increased the target task success range used in RARL from
$175^{th}$
policy network in the source task and the target task with torso mass 1 are provided in Appendix E. Finally, using EACC-RARL and early stopping we have increased the target task success range used in RARL from
![]() $[2.5,4.75]$
to
$[2.5,4.75]$
to
![]() $[1,9]$
.
$[1,9]$
.
5.4.2. The gravity environments
In this set of experiments, we will assess our methods in a large range
![]() $[0.5G_{Earth},1.75G_{Earth}]$
of gravity tasks. For these tasks, we will use the same policy buffer created using SC-PPO and different variations of RARL for the hopper morphology experiments.
$[0.5G_{Earth},1.75G_{Earth}]$
of gravity tasks. For these tasks, we will use the same policy buffer created using SC-PPO and different variations of RARL for the hopper morphology experiments.
Table V. Performance of ACC-RARL.


Figure 11. Performance of EACC-RARL, ESC-RARL, and ERARL on target tasks with torso mass (a) 7 and (b) 8.
Table VI. Performance of EACC-RARL.


Figure 12. (a) Hopper that has torso mass of 9 units, and (b) Performance of EACC-RARL, ESC-RARL, and ERARL on target task with torso mass 9.
The performance evaluations in Figs. 13(a) and (b) prove that training with curriculum and maximum entropy changes the number of generalizable policy iterations in
![]() $0.5G_{Earth}$
target task. ESC-PPO included in Fig. 13(b) still performs poorly compared to adversarial techniques. Although the improvement is negligible, only for this case the entropy regularized SC-PPO (ESC-PPO) performs better than the SC-PPO.
$0.5G_{Earth}$
target task. ESC-PPO included in Fig. 13(b) still performs poorly compared to adversarial techniques. Although the improvement is negligible, only for this case the entropy regularized SC-PPO (ESC-PPO) performs better than the SC-PPO.

Figure 13. Performance of (a) SC-PPO, ACC-RARL, SC-RARL and RARL, and (b) ESC-PPO, ACC-RARL, ESC-RARL, and RARL with curriculum on target environment with gravity = −4.905 (
![]() $0.5G_{Earth}$
).
$0.5G_{Earth}$
).
Policies trained with SC-PPO and adversarial methods can be transferred to the target task with gravity = −14.715 in Fig. 14(a). Figure 14(b) shows that using entropy regularized methods ESC-RARL and ERARL, not only increased the average reward per episode but also increased the number of generalizable policy iterations.

Figure 14. Performance of (a) SC-PPO, ACC-RARL, SC-RARL and RARL, and (b) ACC-RARL, ESC-RARL and ERARL on target environment with gravity = −14.715 (
![]() $1.5G_{Earth}$
).
$1.5G_{Earth}$
).
As the target task gets harder by moving further away from the source task, the best-performing policy iterations are aggregated around earlier iterations similar to the torso mass and the delivery humanoid target tasks. This concavity is analogous to the convexity of the test error curve in supervised learning problems where earlier training iterations lead to underfitting and the later iterations overfit to the training set. The regularization effect of early stopping is pivotal in increasing the generalization capacity. The domain randomization in SC-RARL does not suffice for generalization in harder target tasks when gravity is
![]() $1.75G_{Earth}$
(Fig. 15(a)). We observe that encouraging the exploration of the protagonist policy and the adversary through the inclusion of entropy bonus increases the performance of adversarial algorithms in Fig. 15(b). Results in the gravity environments are in line with the morphology experiments. Above all, entropy regularized adversarial techniques, early stopping, and SC produce competitive results in hard target tasks.
$1.75G_{Earth}$
(Fig. 15(a)). We observe that encouraging the exploration of the protagonist policy and the adversary through the inclusion of entropy bonus increases the performance of adversarial algorithms in Fig. 15(b). Results in the gravity environments are in line with the morphology experiments. Above all, entropy regularized adversarial techniques, early stopping, and SC produce competitive results in hard target tasks.

Figure 15. Performance of (a) SC-PPO, ACC-RARL, SC-RARL and RARL, and (b) EACC-RARL, ESC-RARL and ERARL on target environment with gravity
![]() $= -17.1675 \left(1.75G_{Earth}\right)$
.
$= -17.1675 \left(1.75G_{Earth}\right)$
.

Figure 16. Torque commands (Nm) for the source task.

Figure 17. Torque commands (Nm) for the target task with torso mass = 1.
6. Discussion
Deep RL and Model Predictive Control (MPC) have shown promising results for legged locomotion. MPC is a model-based algorithm used to find an optimal control action in real time. Due to online computation at each timestep, MPC algorithms are computationally expensive and prone to the curse of dimensionality [Reference Whitman, Travers and Choset43]. In contrast, data-driven RL algorithms are deployed after training and only require forward propagation for policy networks or online lookup for discrete table representations. Another drawback of MPC algorithms is their dependence on an accurate dynamics model. Developing robot-specific dynamics requires expert knowledge and task-specific assumptions. On the other hand, deep RL algorithms can recover control actions within time constraints without tailored heuristics and detailed domain knowledge with sufficient training data.
Deep RL algorithms exploit the high representational capacity of neural networks to achieve more efficient control behavior than MPC algorithms. However, the black-box optimization in deep RL leads to the loss of intuition for the control behavior. Hence, a limitation of neural network-based policy gradient algorithms, including our approach, is the lack of human interpretability. Conversely, MPC is advantageous for control tasks that require specific modifications or human interpretations. Another limitation of the proposed approaches is the space requirement. As the number of recording intervals and the complexity of the model increase, the space requirement increases. Tuning the intervals and discarding the models based on validation in a proxy task can mitigate this problem.
Recent advances in deep RL and MPC accelerated the research in the real-world application of legged locomotion. One promising work on the application of an optimization-based control algorithm to a quadrupedal robot is ref. [Reference Bledt and Kim44], where a data-driven approach is used to extract more sophisticated heuristics with Regularized Predictive Control. Although sim-to-real RL is challenging, recent works [Reference Haarnoja, Zhou, Ha, Tan, Tucker and Levine8, Reference Li, Cheng, Peng, Abbeel, Levine, Berseth and Sreenath9, Reference Ha, Xu, Tan, Levine and Tan10, Reference Gangapurwala, Mitchell and Havoutis5, Reference Hwangbo, Lee, Dosovitskiy, Bellicoso, Tsounis, Koltun and Hutter11, Reference Tan, Zhang, Coumans, Iscen, Bai, Hafner, Bohez and Vanhoucke12, Reference Peng, Coumans, Zhang, Lee, Tan and Levine13] show that RL algorithms are robust and applicable to real robotics platforms. Gangapurwala et al. show promising results on the safety-critical robust application of model-free RL on a real ANYmal quadruped robot using guided constrained policy optimization [Reference Gangapurwala, Mitchell and Havoutis5]. Similarly, we use model-free RL to circumvent limitations of the estimations and constraints imposed on the dynamics in MPC. In ref. [Reference Li, Cheng, Peng, Abbeel, Levine, Berseth and Sreenath9], Li et al. used a model-free RL framework for locomotion of a real bipedal human-sized Cassie robot. Using the policies trained in MuJoCo simulator, the Cassie robot can fast walk outdoors, side walk, turn, recover from foot sliding, walk with unknown load, and on anti-slip and slippery surfaces. Li et al. used domain randomization during training to increase robustness. The techniques they used in the simulator include joint damping, noise injection, communication delay, modification of ground friction and mass.
We hope to apply our methods to the Cassie robot for future work. Following the similar procedure in ref. [Reference Li, Cheng, Peng, Abbeel, Levine, Berseth and Sreenath9], we will use a high fidelity simulated environment before deploying the policy on the real robot. In particular, we wish to replicate a modification of the friction and morphology experiments discussed in this work.
7. Conclusion
In this study, we propose a set of methods to extract generalizable knowledge from a single source task. Training independently for each task is a customary sample inefficient process in deep RL. With each environment interaction, the agent’s strategy of solving the source task is expected to advance. However, we find that the transferability of these strategies to similar tasks relies significantly on the number of environment interactions in the source task. The best strategy to solve the source task fails substantially in the target task.
Our experiments show that the performance of transfer RL algorithms is dramatically dependant on the choice of hyperparameters and the number of policy iterations used in the training of the source task. This dependency affects the reproducibility and evaluation accuracy of the algorithms in transfer RL. We addressed this issue in 19 different transfer RL experiments to show how experimental results can be manipulated in favor of an algorithm in the transfer RL domain.
In our work, we proposed keeping a policy buffer to capture different skills because source task performance is not indicative of target task performance. Accordingly, transferring the policy with the best source task performance to the target task becomes a less adequate evaluation technique as the difference between the source and target task increases. In line with this, we suggest using a proxy validation task to extract the generalizable policies. To account for the early stopping regularization technique, we propose the inclusion of the policy iteration to the hyperparameter set. After this inclusion, we have retrieved the generalizable skills that generate high rewards in the target tasks.
We introduced SC-PPO and early stopping as a regularization technique in transfer RL. Training SC-PPO promotes the elimination of samples that overfit the source task. We experimentally show that these robust policies generate a higher jumpstart performance than the baseline in the target tasks. Using SC-PPO and early stopping, we transferred the forward locomotion skills of a standard humanoid to humanoids with different morphologies (a taller humanoid, a shorter humanoid, and a delivery humanoid), humanoids in environments with different gravities (0.5G, 1.5G, and 1.75G), and a humanoid in an environment with 3.5 times the ground friction coefficient of the source task. Moreover, our results show that we can increase the extrapolation range of Hopper morphology tasks from the range of [2.5, 4.75] used in RARL to refs. [Reference Gupta, Eppner, Levine and Abbeel1, Reference Todorov, Erez and Tassa6] via SC-PPO and early stopping. We applied the same technique to transfer the skills of a hopper to the target task with gravity 1.5G.
We conducted a comparative analysis with RARL with different critic methods, entropy bonus, and curriculum learning. Our results show that the choice of hyperparameters and training iteration affect the generalization capacity substantially in adversarial RL. Using entropy regularized ACC-RARL and early stopping via policy buffer, we have increased the extrapolation range of Hopper torso mass tasks from the range of [2.5, 4.75] used in RARL to refs. [Reference Gupta, Eppner, Levine and Abbeel1, Reference Li, Cheng, Peng, Abbeel, Levine, Berseth and Sreenath9]. We prove that a hopper is capable of performing forward locomotion in a target task in the range of [0.5G, 1.75G] by learning in the source task with regularized adversarial RL. Using entropy regularized adversarial RL significantly increased the performance on target tasks and the number of generalizable policies extracted from the source task.
We believe that the first step of determining the most promising policy parameters lies in the accurate parameterization of the source and target task space. In the future, we plan to investigate the relationship between the environment parameters and the source task training hyperparameters.
Author’s contributions
Suzan Ece Ada designed and implemented the research and wrote the manuscript. Emre Uğur and H. Levent Akin co-directed the research, reviewed and edited the manuscript.
Financial support
This work was supported by the Scientific and Technological Research Council of Turkey (TUBITAK, 118E923) and by the BAGEP Award of the Science Academy.
Competing interests
None.
Ethical considerations
None.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/S0263574722000625.
A. Action spaces
A.1. Humanoid actions
Table VII. Humanoid actions.

A.2. Hopper actions
Table VIII. Hopper actions.

B. Hyperparameters
Table IX. Source task training hyperparameters.
C. Humanoid environment specifications
We use the reward function formulated in Open AI Gym [Reference Brockman, Cheung, Pettersson, Schneider, Schulman, Tang and Zaremba37], a toolkit used for comparing RL methods. The reward function of the humanoid environment,
![]() $r _{ humanoid}$
[Reference Brockman, Cheung, Pettersson, Schneider, Schulman, Tang and Zaremba37], consists of a linear forward velocity reward
$r _{ humanoid}$
[Reference Brockman, Cheung, Pettersson, Schneider, Schulman, Tang and Zaremba37], consists of a linear forward velocity reward
![]() $v_{fwd}$
, a quadratic impact cost
$v_{fwd}$
, a quadratic impact cost
![]() $c_{impact}(s,a)$
with lower bound 10, a quadratic control cost, and an alive bonus
$c_{impact}(s,a)$
with lower bound 10, a quadratic control cost, and an alive bonus
![]() $C _{bonus}$
.
$C _{bonus}$
.
If the z-coordinate of the center of mass of the agent is not in the interval [Reference Gupta, Eppner, Levine and Abbeel1, Reference Rajeswaran, Kumar, Gupta, Schulman, Todorov and Levine2], the episode terminates.
D. Hopper environment specifications
The reward function of the hopper environment in Open AI Gym [Reference Brockman, Cheung, Pettersson, Schneider, Schulman, Tang and Zaremba37] consists of linear forward velocity reward
![]() $v_{fwd}$
, sum of squared actions
$v_{fwd}$
, sum of squared actions
![]() $\sum{a^{2}}$
, and an alive bonus
$\sum{a^{2}}$
, and an alive bonus
![]() $C_{bonus}$
.
$C_{bonus}$
.


































