Published online by Cambridge University Press: 13 March 2023
The goal of few-shot semantic segmentation is to learn a segmentation model that can segment novel classes in queries when only a few annotated support examples are available. Due to large intra-class variations, the building of accurate semantic correlation remains a challenging job. Current methods typically use 4D kernels to learn the semantic correlation of feature maps. However, they still face the challenge of reducing the consumption of computation and memory while keeping the availability of correlations mined by their methods. In this paper, we propose the adaptively mining correlation network (AMCNet) to alleviate the aforementioned issues. The key points of AMCNet are the proposed adaptive separable 4D kernel and the learnable pyramid correlation module, which form the basic block for correlation encoder and provide a learnable concatenation operation over pyramid correlation tensors, respectively. Experiments on the PASCAL VOC 2012 dataset show that our AMCNet surpasses the state-of-the-art method by
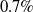 $0.7\%$
and
$0.7\%$
and
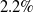 $2.2\%$
on 1-shot and 5-shot segmentation scenarios, respectively.
$2.2\%$
on 1-shot and 5-shot segmentation scenarios, respectively.