Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-05T13:38:27.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing a Manipulator Regressor Without Acceleration Feedback

Published online by Cambridge University Press:  09 March 2009

Jing Yuan  and
Yury Stepenanko
Jing Yuan
Affiliation:
Department of Mechanical Engineering, University of Victoria, Victoria, B.C. V8W 2Y 2 (Canada)
Yury Stepenanko
Affiliation:
Department of Mechanical Engineering, University of Victoria, Victoria, B.C. V8W 2Y 2 (Canada)
Get access Rights & Permissions [Opens in a new window]

Summary

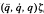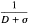A manipulator regressor is an n x l matrix function in the dynamic expression τ = Y r or τ = W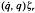r, which linearizes the robotic dynamics with respect to a properly defined inertia parameter vector ζr є R1. Many modern adaptive controllers require on-line computation of a regressor to estimate the unknown inertia parameters and ensure robustness of the closed-loop system.

While the computation of Y 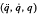is studied by Atkeson, An and Hollerbach1 and Khosla and Kanade,2 the computation of W 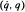for a general n–link robot has not been reported in the literature. This paper presents an algorithm to compute W 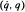for a general n–link robotic manipulator. The variables used to construct the regressor matrix are directly available from the outward iteration of a Newton-Euler algorithm; some additional arithmetic operations and first-order, low-pass filtering are needed. The identification of unknown inertia parameters is also discussed.

Keywords

Manipulator regressorRobot dynamicsInertia parametersAcceleration feedback
Type
Article
Information
Robotica , Volume 10 , Issue 3 , May 1992 , pp. 269 - 275
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Atkeson, C., An, C. and Hollerbach, J., “Estimation of Inertial Parameters of Manipulator Loads and Links” Robotics Research, (MIT Press, Cambridge, 1985) pp. 221–228.Google Scholar
2.Khosla, P. and Kanade, T., “Parameter Identification of Robot Dynamics” Proc. IEEE Conf. Decision and Control,Fort Lauderdale, Fia. (12, 1985) pp. 1754–1760.CrossRefGoogle Scholar
3.Paul, R.C., “Modeling, Trajectory Calculation and Servoing of a Computer Controlled Arm”, AIM-117, Stanford University Artificial Intelligence Laboratory (1972).CrossRefGoogle Scholar
4.Bejczy, A.K., “Robot Arm Dynamics and Control” JPL NASA Technical Memor. 33–669 (02, 1974).Google Scholar
5.Lewis, R.A., “Autonomous Manipulation on a Robot: Summary of Manipulator Software Functions” JPL Technical Memor. 33–679 (03, 1974).Google Scholar
6.Markiewicz, B.R., “Analysis of the Computed Torque Drive Method and Comparison with Conventional Positive Servo for a Computer-Controlled Manipulator” JPL Technical Memor. 33–601 (03, 1973).Google Scholar
7.Luh, J.Y.S., Walker, M.W. and Paul, R.P., “Resolved-Acceleration Control of Mechanical Manipulators” IEEE Trans. Auto. Contr. AC-25, 3, 428–474 (1980).Google Scholar
8.Luh, J.Y.S., Walker, M.W. and Paul, R.P., “On-Line Computation Scheme for Mechanical Manipulators” Trans. ASME J. Dynam. Syst. Meas. Contr. 102, 69–76 (1980).CrossRefGoogle Scholar
9.Craig, J.J., Adaptive Control of Mechanical Manipulators (Addison-Wesley, Reading, Massachusetts, 1988).Google Scholar
10.Craig, J., Hsu, P. and Sastri, S., “Adaptive control of mechanical manipulators” Proc. IEEE Conference on Robotics and Automation,San Francisco, Calif. (1986) pp. 243–248.Google Scholar
11.Slotine, J.J.E. and Li, W., “Composite Adaptive Control of Robot Manipulators” Automatica 25, No. 4, 509–519 (1989).CrossRefGoogle Scholar
12.Slotine, J.E. and Li, W., “Adaptive manipulator control: a case study” IEEE Trans. Automat. Control 33, 11, 995–1003 (1988).CrossRefGoogle Scholar
13.Sadegh, N. and Horowitz, R., “Stability and Robustness Analysis of A Class of Adaptive Controllers for Robotic Manipulators”, Inter J. Robotics Research 9, 3, 74–92 (1990).CrossRefGoogle Scholar
14.Bayard, D.S. and Wen, J.T., “New Class of Control Laws for Robotic Manipulators Part 1. Adaptive Cose” inter. J. Control 47, 5, 1387–1406 (1988).CrossRefGoogle Scholar
15.Middleton, R.H. and Goodwin, G.C., “Adaptive Computed Torque Control for Rigid Link Manipulators” Proc. IEEE Conf. Decision and Control 68–73, Athens (12 1986) pp. 68–73.Google Scholar
16.Hsu, P., Bodson, M., Sastry, S. and Paden, B., “Adaptive Identification and Control for Manipulators without Using Joint Accelerations” Proc. IEEE Int. Conf. Robotics and Automation, Raleigh, N.C. (1986) pp. 1210–1215.Google Scholar
17.Craig, J.J., Introduction to Robotics Mechanics and Control (Addison-Wesley, Reading, Massachusetts, 1986).Google Scholar
18.Spong, M.W. and Vidyasagar, M., Robot Dynamics and Control (J. Wiley and Son., New York, 1989).Google Scholar