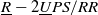 $\underline{R}-2\underline{U}PS/RR$ mechanism
$\underline{R}-2\underline{U}PS/RR$ mechanismPublished online by Cambridge University Press: 14 September 2022
In order to make the designed ankle robotic system simpler, practical, and clinically oriented, we developed a novel
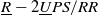 $\underline{R}-2\underline{U}PS/RR$
ankle rehabilitation robot with a variety of training functions covering all the required ranges of motion of the ankle joint complex (AJC), where
$\underline{R}-2\underline{U}PS/RR$
ankle rehabilitation robot with a variety of training functions covering all the required ranges of motion of the ankle joint complex (AJC), where
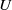 $U$
,
$U$
,
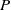 $P$
,
$P$
,
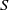 $S$
, and
$S$
, and
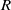 $R$
denote universal, prismatic, spherical, and revolute joints, respectively, and the underlined letter denotes the actuated joint. The robot was designed with three degrees of freedom (DOFs), with a series
$R$
denote universal, prismatic, spherical, and revolute joints, respectively, and the underlined letter denotes the actuated joint. The robot was designed with three degrees of freedom (DOFs), with a series
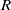 $R$
mechanism and a
$R$
mechanism and a
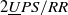 $2\underline{U}PS/RR$
parallel mechanism. The main advantage is that the height of the robot is very low, which is convenient for clinical use by patients. At first, the mechanism design and inverse solution of positions were introduced in detail. Then, the patient-passive exercise based on the predefined trajectory tracking and patient-active exercise based on the spring model were developed to satisfy different rehabilitation stages. Finally, experiments with healthy subjects were conducted to verify the effectiveness of the developed patient-passive and patient-active exercises of the developed ankle rehabilitation robot, with results compared with the existing ankle robotic system showing good trajectory tracking performance and interactive performance.
$2\underline{U}PS/RR$
parallel mechanism. The main advantage is that the height of the robot is very low, which is convenient for clinical use by patients. At first, the mechanism design and inverse solution of positions were introduced in detail. Then, the patient-passive exercise based on the predefined trajectory tracking and patient-active exercise based on the spring model were developed to satisfy different rehabilitation stages. Finally, experiments with healthy subjects were conducted to verify the effectiveness of the developed patient-passive and patient-active exercises of the developed ankle rehabilitation robot, with results compared with the existing ankle robotic system showing good trajectory tracking performance and interactive performance.