Published online by Cambridge University Press: 05 June 2023
This paper presents backstepping control and backstepping constraint control approaches for a quadrotor unmanned aerial vehicle (UAV) control system. The proposed methods are applied to a Parrot Mambo drone model to control rotational motion along the  $x$,
$x$, 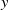 $y$, and
$y$, and  $z$ axes during hovering and trajectory tracking. In the backstepping control approach, each state of the system controls the previous state and is called “virtual control.” The last state is controlled by the real control input. The idea is to compute, in several steps, a control law that ensures the asymptotic stability of the system. The backstepping constraint control method, based on barrier Lyapunov functions (BLFs), is designed not only to track the desired trajectory but also to guarantee no violation of the position and angle constraints. Symmetric BLFs are introduced in the design of the controller. A nonlinear mathematical model is considered in this study. Based on Lyapunov stability theory, it can be concluded that the proposed controllers can guarantee the stability of the UAV system and the state converges asymptotically to the desired trajectory. To make the control robust, an adaptation law is applied to the backstepping control that estimates the unknown parameters and ensures their convergence to their respective values. Validation of the proposed controllers was performed by simulation on a flying UAV system.
$z$ axes during hovering and trajectory tracking. In the backstepping control approach, each state of the system controls the previous state and is called “virtual control.” The last state is controlled by the real control input. The idea is to compute, in several steps, a control law that ensures the asymptotic stability of the system. The backstepping constraint control method, based on barrier Lyapunov functions (BLFs), is designed not only to track the desired trajectory but also to guarantee no violation of the position and angle constraints. Symmetric BLFs are introduced in the design of the controller. A nonlinear mathematical model is considered in this study. Based on Lyapunov stability theory, it can be concluded that the proposed controllers can guarantee the stability of the UAV system and the state converges asymptotically to the desired trajectory. To make the control robust, an adaptation law is applied to the backstepping control that estimates the unknown parameters and ensures their convergence to their respective values. Validation of the proposed controllers was performed by simulation on a flying UAV system.