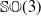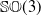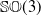Nomenclature
-
 $\mathbb{SO}(3)$
$\mathbb{SO}(3)$
-
Special orthogonal group in
 $3$
dimensions
$3$
dimensions -
 $\boldsymbol{R}_X({\cdot})$
$\boldsymbol{R}_X({\cdot})$
-
Rotation matrix for rotation about the
 $X$
-axis
$X$
-axis -
 $\boldsymbol{R}_Y({\cdot})$
$\boldsymbol{R}_Y({\cdot})$
-
Rotation matrix for rotation about the
 $Y$
-axis
$Y$
-axis -
 $\boldsymbol{R}_Z({\cdot})$
$\boldsymbol{R}_Z({\cdot})$
-
Rotation matrix for rotation about the
 $Z$
-axis
$Z$
-axis -
 $\{\alpha, \beta, \gamma \}$
$\{\alpha, \beta, \gamma \}$
-
The sequence of three Euler angles used in this article
-
 $\underline{({\cdot})}$
$\underline{({\cdot})}$
-
Lower limit of Euler angle
 $({\cdot})$
$({\cdot})$
-
 $\overline{({\cdot})}$
$\overline{({\cdot})}$
-
Upper limit of Euler angle
 $({\cdot})$
$({\cdot})$
-
 $\boldsymbol{k}$
$\boldsymbol{k}$
-
A unit vector in
 ${\mathbb{R}}^3$
describing the axis of rotation
${\mathbb{R}}^3$
describing the axis of rotation -
 $\psi$
$\psi$
-
Angle of rotation about the axis
 $\boldsymbol{k}$
$\boldsymbol{k}$
-
 $\phi$
$\phi$
-
Critical value of
 $\psi$
$\psi$
-
 $\mathcal{E}$
$\mathcal{E}$
-
Space of Euler angles
-
 ${\mathcal{R}}$
${\mathcal{R}}$
-
Space of Rodrigues parameters
-
 $\mathcal{V}_{\mathcal{E}}$
$\mathcal{V}_{\mathcal{E}}$
-
A cuboid in
 $\mathcal{E}$
$\mathcal{E}$
-
 $\mathcal{F}_{({\cdot})}$
$\mathcal{F}_{({\cdot})}$
-
A face (
 $\cdot$
) of
$\cdot$
) of
 $\mathcal{V}_{\mathcal{E}}$
; e.g.,
$\mathcal{V}_{\mathcal{E}}$
; e.g.,
 $\mathcal{F}_{{\overline{\gamma }}}$
,
$\mathcal{F}_{{\overline{\gamma }}}$
,
 $\mathcal{F}_{{\underline{\gamma }}}$
, etc.
$\mathcal{F}_{{\underline{\gamma }}}$
, etc. -
 $\mathcal{V}_{\mathcal{R}}$
$\mathcal{V}_{\mathcal{R}}$
-
A region in
 $\mathcal{R}$
$\mathcal{R}$
-
 ${\mathcal{Q}}_{({\cdot})}$
${\mathcal{Q}}_{({\cdot})}$
-
A bounding surface of
 $\mathcal{R}$
, corresponding to
$\mathcal{R}$
, corresponding to
 $\mathcal{F}_{({\cdot})}$
$\mathcal{F}_{({\cdot})}$
-
 $\mathcal{S}$
$\mathcal{S}$
-
A sphere that is tangent to one or more surfaces of
 $\mathcal{V}_{\mathcal{R}}$
$\mathcal{V}_{\mathcal{R}}$
-
 $r$
$r$
-
The radius of
 $\mathcal{S}$
$\mathcal{S}$
-
 $\overline{{\mathcal{S}}}$
$\overline{{\mathcal{S}}}$
-
The largest sphere that fits inside
 $\mathcal{V}_{\mathcal{R}}$
$\mathcal{V}_{\mathcal{R}}$
-
 $\overline{r}$
$\overline{r}$
-
The radius of
 $\overline{{\mathcal{S}}}$
$\overline{{\mathcal{S}}}$
-
 $\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
$\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
-
Global frame of reference in
 $\mathcal{R}$
$\mathcal{R}$
-
 $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
-
Local frame of reference in
 $\mathcal{R}$
$\mathcal{R}$
-
 $\mathcal{U}_{({\cdot})}$
$\mathcal{U}_{({\cdot})}$
-
A quadric in
 $\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
corresponding to the face
$\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
corresponding to the face
 $\mathcal{F}_{({\cdot})}$
in
$\mathcal{F}_{({\cdot})}$
in
 $\mathcal{E}$
$\mathcal{E}$
-
 $\mathcal{U}^{\prime}_{({\cdot})}$
$\mathcal{U}^{\prime}_{({\cdot})}$
-
A quadric in
 $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
corresponding to the face
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
corresponding to the face
 $\mathcal{F}_{({\cdot})}$
in
$\mathcal{F}_{({\cdot})}$
in
 $\mathcal{E}$
$\mathcal{E}$
-
 $\mathcal{P}^{\prime}_2$
$\mathcal{P}^{\prime}_2$
-
A plane in
 $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
defined as
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
defined as
 $d^{\prime}_2=0$
$d^{\prime}_2=0$
-
 $\mathcal{P}^{\prime}_3$
$\mathcal{P}^{\prime}_3$
-
A plane in
 $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
defined as
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
defined as
 $d^{\prime}_3=0$
$d^{\prime}_3=0$
-
 ${\mathcal{S}}^{\prime}$
${\mathcal{S}}^{\prime}$
-
A sphere in
 $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
-
 $\mathcal{X}_{\text{e}}$
$\mathcal{X}_{\text{e}}$
-
An ellipse resulting from the intersection of
 $\mathcal{P}_2$
with
$\mathcal{P}_2$
with
 ${\mathcal{U}^{\prime}_{{\overline{\gamma }}}}$
${\mathcal{U}^{\prime}_{{\overline{\gamma }}}}$
-
 $\mathcal{C}_{\text{e}}$
$\mathcal{C}_{\text{e}}$
-
A circle resulting from the intersection of
 $\mathcal{P}_2$
with
$\mathcal{P}_2$
with
 ${\mathcal{S}}^{\prime}$
${\mathcal{S}}^{\prime}$
-
 $\mathcal{X}_{\text{h}}$
$\mathcal{X}_{\text{h}}$
-
A hyperbola resulting from the intersection of
 $\mathcal{P}_3$
with
$\mathcal{P}_3$
with
 ${\mathcal{U}^{\prime}_{{\overline{\gamma }}}}$
${\mathcal{U}^{\prime}_{{\overline{\gamma }}}}$
-
 $\mathcal{C}_{\text{h}}$
$\mathcal{C}_{\text{h}}$
-
A circle resulting from the intersection of
 $\mathcal{P}_3$
with
$\mathcal{P}_3$
with
 ${\mathcal{S}}^{\prime}$
${\mathcal{S}}^{\prime}$
- CAS
-
Computer algebra system
1. Introduction
Obtaining an accurate description of the workspace of a spatial manipulator is extremely important from the perspectives of its design as well as operation. However, this problem is also one of the most involved ones. While the workspace of any manipulator is a subset of
![]() $\mathbb{SE}(3)$
, the nature (i.e., rotational, or translational, or a combination of the two) of the degree-of-freedom (DoF) and the ranges of different outputs depend on the architecture of the manipulator as well as the ranges of input motions. If the output of a manipulator is neither purely translational (e.g., Cartesian robots, Delta manipulator (see, e.g., [Reference Merlet9], p. 23)) nor entirely rotational (e.g., spherical robots, Agile Eye (see, e.g., [Reference Merlet9], pp. 36–37)), its workspace has to be described separately as orientation and translation workspaces. Since rotations and translations are physically distinct entities, there is no common global metric that applies to both, as noted in, for example, [Reference Di Gregorio10]. In simpler terms, while one can use metrics based on the
$\mathbb{SE}(3)$
, the nature (i.e., rotational, or translational, or a combination of the two) of the degree-of-freedom (DoF) and the ranges of different outputs depend on the architecture of the manipulator as well as the ranges of input motions. If the output of a manipulator is neither purely translational (e.g., Cartesian robots, Delta manipulator (see, e.g., [Reference Merlet9], p. 23)) nor entirely rotational (e.g., spherical robots, Agile Eye (see, e.g., [Reference Merlet9], pp. 36–37)), its workspace has to be described separately as orientation and translation workspaces. Since rotations and translations are physically distinct entities, there is no common global metric that applies to both, as noted in, for example, [Reference Di Gregorio10]. In simpler terms, while one can use metrics based on the
![]() $L_1$
or
$L_1$
or
![]() $L_2$
norms in
$L_2$
norms in
![]() ${\mathbb{R}}^2/{\mathbb{R}}^3$
to describe reachable workspaces in terms of geometrical shapes, for example, parallelograms/parallelepipeds or circles/spheres, respectively, these metrics are not admissible in
${\mathbb{R}}^2/{\mathbb{R}}^3$
to describe reachable workspaces in terms of geometrical shapes, for example, parallelograms/parallelepipeds or circles/spheres, respectively, these metrics are not admissible in
![]() $\mathbb{SO}(3)$
, at least in a global sense. Moreover, the valid metrics in
$\mathbb{SO}(3)$
, at least in a global sense. Moreover, the valid metrics in
![]() $\mathbb{SO}(3)$
depend on the parametrisation employed. For instance, one can indeed describe a sphere in
$\mathbb{SO}(3)$
depend on the parametrisation employed. For instance, one can indeed describe a sphere in
![]() $\mathbb{SO}(3)$
using the Rodrigues parameter representation of it, but only in the vicinity of the origin (i.e., the point in
$\mathbb{SO}(3)$
using the Rodrigues parameter representation of it, but only in the vicinity of the origin (i.e., the point in
![]() $\mathbb{SO}(3)$
corresponding to zero net rotation); see, for example, [Reference Nag and Bandyopadhyay11], for the details, and [Reference Pernkopf and Husty12], for the original idea, albeit in the context of the unit quaternion representation of
$\mathbb{SO}(3)$
corresponding to zero net rotation); see, for example, [Reference Nag and Bandyopadhyay11], for the details, and [Reference Pernkopf and Husty12], for the original idea, albeit in the context of the unit quaternion representation of
![]() $\mathbb{SO}(3)$
.
$\mathbb{SO}(3)$
.
A detailed survey of various parametrisations of
![]() $\mathbb{SO}(3)$
may be found in [Reference Shuster13]. It discusses the Euler angles, axis-azimuth representation, Euler–Rodrigues parameters, quaternions, Rodrigues parameters, Cayley–Klein parameters and modified Rodrigues parameters and documents the relationships between these representations. The maps between the unit quaternions and Rodrigues parameters (also known as Gibbs vector (see [Reference Wilson and Gibbs14], p. 340 and [Reference Haslwanter15], pp. 64–66)) and Euler angles are presented in [Reference Spring16] as well. Various parametrisations were studied in [Reference Wang, Chang, Xu and Zou17] to estimate the errors of orientation parameters in Helmert transformation models. Further, representations of rotation were grouped into two categories: (a) redundant representations, which include the “direction cosine matrix” and the unit quaternions and (b) minimal representations, which include the axis–angle representation, Rodrigues parameters and modified Rodrigues parameters.
$\mathbb{SO}(3)$
may be found in [Reference Shuster13]. It discusses the Euler angles, axis-azimuth representation, Euler–Rodrigues parameters, quaternions, Rodrigues parameters, Cayley–Klein parameters and modified Rodrigues parameters and documents the relationships between these representations. The maps between the unit quaternions and Rodrigues parameters (also known as Gibbs vector (see [Reference Wilson and Gibbs14], p. 340 and [Reference Haslwanter15], pp. 64–66)) and Euler angles are presented in [Reference Spring16] as well. Various parametrisations were studied in [Reference Wang, Chang, Xu and Zou17] to estimate the errors of orientation parameters in Helmert transformation models. Further, representations of rotation were grouped into two categories: (a) redundant representations, which include the “direction cosine matrix” and the unit quaternions and (b) minimal representations, which include the axis–angle representation, Rodrigues parameters and modified Rodrigues parameters.
It is interesting to note that among solids of various shapes, cuboids have been commonly preferred for describing subsets of
![]() $\mathbb{SO}(3)$
in the existing literature, for example, in [Reference Monsarrat and Gosselin18–Reference Merlet20]. Presumably, the popularity of this shape stemmed from its simplicity and utility in the Cartesian framework, where the
$\mathbb{SO}(3)$
in the existing literature, for example, in [Reference Monsarrat and Gosselin18–Reference Merlet20]. Presumably, the popularity of this shape stemmed from its simplicity and utility in the Cartesian framework, where the
![]() $L_1$
norm is well-defined. However, in the context of
$L_1$
norm is well-defined. However, in the context of
![]() $\mathbb{SO}(3)$
, the physical and mathematical implications of this choice of shape are not clear, since the validity of the said norm in
$\mathbb{SO}(3)$
, the physical and mathematical implications of this choice of shape are not clear, since the validity of the said norm in
![]() $\mathbb{SO}(3)$
is not established (to the best of the authors’ knowledge). Yet, a statement akin to “The end-effector is capable of executing roll, pitch and yaw motions to the extent of
$\mathbb{SO}(3)$
is not established (to the best of the authors’ knowledge). Yet, a statement akin to “The end-effector is capable of executing roll, pitch and yaw motions to the extent of
![]() $\pm{\overline{\alpha }}, \pm{\overline{\beta }}, \pm{\overline{\gamma }}$
degrees”, where
$\pm{\overline{\alpha }}, \pm{\overline{\beta }}, \pm{\overline{\gamma }}$
degrees”, where
![]() ${\overline{\alpha }},{\overline{\beta }},{\overline{\gamma }}$
are the specified limits, is common to find in the mechanical specifications of a robot, especially parallel robots. Table I illustrates this point, in which the orientation workspaces of several commercially available Stewart platform manipulators have been specified following the websites of the respective manufacturers. All of these specifications are in terms of ranges of Euler angles by the respective manufacturers. In spite of its popularity, such a description leaves several pertinent questions unanswered, the first among these being whether these limits are attained simultaneously, or each of these limits is supposed to be achieved individually, only one at a time. The other questions pertain to whether these limits are applicable in the body-fixed or the space-fixed convention of rotationsFootnote
1
; and given the ranges of Euler angles, what the permissible angle of rotation might be about any given arbitrary axis in space. The last question relates itself to the spherical representation of
${\overline{\alpha }},{\overline{\beta }},{\overline{\gamma }}$
are the specified limits, is common to find in the mechanical specifications of a robot, especially parallel robots. Table I illustrates this point, in which the orientation workspaces of several commercially available Stewart platform manipulators have been specified following the websites of the respective manufacturers. All of these specifications are in terms of ranges of Euler angles by the respective manufacturers. In spite of its popularity, such a description leaves several pertinent questions unanswered, the first among these being whether these limits are attained simultaneously, or each of these limits is supposed to be achieved individually, only one at a time. The other questions pertain to whether these limits are applicable in the body-fixed or the space-fixed convention of rotationsFootnote
1
; and given the ranges of Euler angles, what the permissible angle of rotation might be about any given arbitrary axis in space. The last question relates itself to the spherical representation of
![]() ${\mathbb{SO}(3)}$
, that is, one could pose it in the following manner: what is the maximum angle of rotation that one can attain if the axis of such rotations can have any direction in space, that is, the axis represents an arbitrary point on the unit sphere
${\mathbb{SO}(3)}$
, that is, one could pose it in the following manner: what is the maximum angle of rotation that one can attain if the axis of such rotations can have any direction in space, that is, the axis represents an arbitrary point on the unit sphere
![]() $\mathbb{S}^2$
?
$\mathbb{S}^2$
?
Table I. Few examples of commercially available Stewart platform manipulators whose orientation workspaces have been specified by the respective manufacturers in terms of ranges of Euler angles. The ranges can be uniform or non-uniform, as seen in these samples.

To find answers to the above questions, this article turns to the Rodrigues parameter description of
![]() $\mathbb{SO}(3)$
, which addresses all of these adequately and naturally. Firstly, it looks at “boxes” or “cuboids” or “parallelepipeds” [Reference Yang, Lin, Mustafa, Chen and Yeo23] defined in
$\mathbb{SO}(3)$
, which addresses all of these adequately and naturally. Firstly, it looks at “boxes” or “cuboids” or “parallelepipeds” [Reference Yang, Lin, Mustafa, Chen and Yeo23] defined in
![]() $\mathbb{SO}(3)$
, terms of Euler angles. These 3D regions or solids are denoted by
$\mathbb{SO}(3)$
, terms of Euler angles. These 3D regions or solids are denoted by
![]() ${\mathcal{V}_{\mathcal{E}}}\in{\mathcal{E}}$
, where
${\mathcal{V}_{\mathcal{E}}}\in{\mathcal{E}}$
, where
![]() $\mathcal{E}$
is the space of Euler angles, henceforth. Different sequences of Euler angles are studied at this stage, including the relations among those. Next, the solids
$\mathcal{E}$
is the space of Euler angles, henceforth. Different sequences of Euler angles are studied at this stage, including the relations among those. Next, the solids
![]() $\mathcal{V}_{\mathcal{E}}$
are mapped to the corresponding solids (denoted by
$\mathcal{V}_{\mathcal{E}}$
are mapped to the corresponding solids (denoted by
![]() $\mathcal{V}_{\mathcal{R}}$
) in the space of Rodrigues parameters (denoted by
$\mathcal{V}_{\mathcal{R}}$
) in the space of Rodrigues parameters (denoted by
![]() $\mathcal{R}$
). Both the body-fixed and space-fixed conventions are covered in this study. It is established that the corner points of the solids corresponding to body-fixed rotations exhibit central symmetry about the origin with the corresponding corners of the solid pertaining to the same rotation expressed in the space-fixed convention. Furthermore, it is observed that the solids
$\mathcal{R}$
). Both the body-fixed and space-fixed conventions are covered in this study. It is established that the corner points of the solids corresponding to body-fixed rotations exhibit central symmetry about the origin with the corresponding corners of the solid pertaining to the same rotation expressed in the space-fixed convention. Furthermore, it is observed that the solids
![]() $\mathcal{V}_{\mathcal{R}}$
have complicated shapes, since these are bounded by six distinct hyperboloids of one sheet (which has been visualised via an animation, appended herewith as the video file surface_animation.gif, albeit showing only two hyperboloids for the sake of clarity) which make it difficult to use them for comparing the extent of the orientation workspaces that they represent. Therefore, a region of regular convex shape of the largest extent needs to be fitted inside the solid
$\mathcal{V}_{\mathcal{R}}$
have complicated shapes, since these are bounded by six distinct hyperboloids of one sheet (which has been visualised via an animation, appended herewith as the video file surface_animation.gif, albeit showing only two hyperboloids for the sake of clarity) which make it difficult to use them for comparing the extent of the orientation workspaces that they represent. Therefore, a region of regular convex shape of the largest extent needs to be fitted inside the solid
![]() $\mathcal{V}_{\mathcal{R}}$
, so that the extent of the orientation workspaces can be related to the dimensions of these regular solids in a quantitative manner. In this article, a spherical shape is chosen to serve this purpose, for reasons explained in detail in Section 3. The radius of the largest sphere that fits in any instance of
$\mathcal{V}_{\mathcal{R}}$
, so that the extent of the orientation workspaces can be related to the dimensions of these regular solids in a quantitative manner. In this article, a spherical shape is chosen to serve this purpose, for reasons explained in detail in Section 3. The radius of the largest sphere that fits in any instance of
![]() $\mathcal{V}_{\mathcal{R}}$
is identified analytically, in the closed form. It is demonstrated that the said radius corresponds to the smallest of the individual ranges of rotations, irrespective of the Euler angle sequence used.
$\mathcal{V}_{\mathcal{R}}$
is identified analytically, in the closed form. It is demonstrated that the said radius corresponds to the smallest of the individual ranges of rotations, irrespective of the Euler angle sequence used.
This article makes two important contributions. Firstly, it brings forth the physical significance of the cuboids defined in the Euler angle space and demonstrates their utility in describing orientation workspaces. Secondly, and perhaps more importantly, by identifying the largest included spheres inside the corresponding solids in the Rodrigues parameter space, a quantitative measure of the size of the orientation workspace is established. These developments have many potential applications in the domain of design and path planning of robot manipulators, particularly those with multiple rotational DoF and restricted orientation workspaces, such as spatial parallel manipulators.
The rest of the article is organised as follows. Section 2 describes the mapping from Euler angles to Rodrigues parameters. Section 3 demonstrates the computation of the largest sphere that fits entirely inside a solid in the space of Rodrigues parameters. The bounding surfaces of the said solid are studied geometrically in Section 4. Numerical examples covering both uniform and non-uniform ranges of Euler angles are presented in Section 5. Section 6 summarises the contributions and discusses their significance. Finally, the article is concluded in Section 7.
2. Mapping of a subset of
 $\mathbb{SO}(3)$
described in Euler angles to the space of Rodrigues parameters
$\mathbb{SO}(3)$
described in Euler angles to the space of Rodrigues parameters
The orientations of a rigid body form the special orthogonal group of three dimensions, denoted by
![]() $\mathbb{SO}(3)$
. A summary of the geometric/algebraic properties of this group has been presented in Appendix A. This group admits numerous representations, the most popular among which, perhaps, are the rotation matrices,
$\mathbb{SO}(3)$
. A summary of the geometric/algebraic properties of this group has been presented in Appendix A. This group admits numerous representations, the most popular among which, perhaps, are the rotation matrices,
![]() $\boldsymbol{R} \in{\mathbb{R}}^{3\times 3}$
, where
$\boldsymbol{R} \in{\mathbb{R}}^{3\times 3}$
, where
![]() $\boldsymbol{R}$
is orthogonal and
$\boldsymbol{R}$
is orthogonal and
![]() $\text{det}(\boldsymbol{R}) = 1$
. These matrices can themselves be expressed variously in terms of different parametrisations, among which the most common may be a sequence of three Euler angles. A generic rotation matrix,
$\text{det}(\boldsymbol{R}) = 1$
. These matrices can themselves be expressed variously in terms of different parametrisations, among which the most common may be a sequence of three Euler angles. A generic rotation matrix,
![]() $\boldsymbol{R}$
, may be expressed as a concatenation of three successive simple rotations about the coordinate axes. For instance, in the body-fixed convention, one could write
$\boldsymbol{R}$
, may be expressed as a concatenation of three successive simple rotations about the coordinate axes. For instance, in the body-fixed convention, one could write
![]() $\boldsymbol{R}={\boldsymbol{R}_Z(\alpha ) \boldsymbol{R}_Y(\beta ) \boldsymbol{R}_X(\gamma )}$
, which constitutes a Z-Y-X or
$\boldsymbol{R}={\boldsymbol{R}_Z(\alpha ) \boldsymbol{R}_Y(\beta ) \boldsymbol{R}_X(\gamma )}$
, which constitutes a Z-Y-X or
![]() $3$
-
$3$
-
![]() $2$
-
$2$
-
![]() $1$
type of rotation,
$1$
type of rotation,
![]() $\alpha, \beta$
, and
$\alpha, \beta$
, and
![]() $\gamma$
being the corresponding Euler angles, respectively. It is known that in the space-fixed convention, the same rotation may be represented by
$\gamma$
being the corresponding Euler angles, respectively. It is known that in the space-fixed convention, the same rotation may be represented by
![]() $\boldsymbol{R}^{\prime}={\boldsymbol{R}_X(\gamma ) \boldsymbol{R}_Y(\beta )\boldsymbol{R}_Z(\alpha )}$
. Considering both the body-fixed and space-fixed conventions, and the sequences of the types Z-Y-X as well as
$\boldsymbol{R}^{\prime}={\boldsymbol{R}_X(\gamma ) \boldsymbol{R}_Y(\beta )\boldsymbol{R}_Z(\alpha )}$
. Considering both the body-fixed and space-fixed conventions, and the sequences of the types Z-Y-X as well as
![]() $Z$
-
$Z$
-
![]() $X$
-
$X$
-
![]() $Z$
, there can be a total of 24 valid sequences of Euler anglesFootnote
2
(for the details, see, e.g., [Reference Craig24], Appendix B). This article will follow the body-fixed convention primarily.
$Z$
, there can be a total of 24 valid sequences of Euler anglesFootnote
2
(for the details, see, e.g., [Reference Craig24], Appendix B). This article will follow the body-fixed convention primarily.
In the Z-Y-X sequence, by choosing
![]() $\alpha, \beta, \gamma \in [{-}\pi, \pi ]$
, one covers
$\alpha, \beta, \gamma \in [{-}\pi, \pi ]$
, one covers
![]() $\mathbb{SO}(3)$
entirely. However, in most practical examples, only proper subsets of
$\mathbb{SO}(3)$
entirely. However, in most practical examples, only proper subsets of
![]() $\mathbb{SO}(3)$
are of interest, since the end-effector of a serial manipulator or the moving platform of a parallel one cannot typically achieve all possible orientations due to practical constraints.Footnote
3
Such a subset is often described via a box or a cuboid
$\mathbb{SO}(3)$
are of interest, since the end-effector of a serial manipulator or the moving platform of a parallel one cannot typically achieve all possible orientations due to practical constraints.Footnote
3
Such a subset is often described via a box or a cuboid
![]() $\mathcal{V}_{\mathcal{E}}$
in the same manner as one would in a Cartesian space [Reference Monsarrat and Gosselin18–Reference Merlet20]:
$\mathcal{V}_{\mathcal{E}}$
in the same manner as one would in a Cartesian space [Reference Monsarrat and Gosselin18–Reference Merlet20]:
In the above and henceforth,
![]() $\underline{({\cdot})}$
and
$\underline{({\cdot})}$
and
![]() $\overline{({\cdot})}$
denote the lower and upper limits of the individual Euler angles, respectively. As in most of the cases reported in the literature, it is assumed in this work that the ranges of individual Euler angles are symmetric about the origin; that is:
$\overline{({\cdot})}$
denote the lower and upper limits of the individual Euler angles, respectively. As in most of the cases reported in the literature, it is assumed in this work that the ranges of individual Euler angles are symmetric about the origin; that is:
The symmetric ranges of Euler angles discussed in the following are divided into two categories, namely: (a) uniform and (b) non-uniform ranges. The ranges are called uniform when
![]() ${\overline{\alpha }}={\overline{\beta }}={\overline{\gamma }}$
and consequently
${\overline{\alpha }}={\overline{\beta }}={\overline{\gamma }}$
and consequently
![]() ${\underline{\alpha }}={\underline{\beta }}={\underline{\gamma }}$
, and non-uniform otherwise. Such ranges are widely used for describing the orientation workspaces of spatial parallel manipulators, such as the Stewart platforms, of which a few examples are listed in Table I. Furthermore, the minimum and maximum limits of Euler angles are required to lie within the ranges
${\underline{\alpha }}={\underline{\beta }}={\underline{\gamma }}$
, and non-uniform otherwise. Such ranges are widely used for describing the orientation workspaces of spatial parallel manipulators, such as the Stewart platforms, of which a few examples are listed in Table I. Furthermore, the minimum and maximum limits of Euler angles are required to lie within the ranges
![]() $(-\pi /2,0)$
and
$(-\pi /2,0)$
and
![]() $(0,\pi /2)$
, respectively, to avoid parametrisation singularities (see, e.g., [Reference Ghosal21], pp. 28–29 and [Reference Murray, Sastry and Zexiang26], p. 33) or gimbal locks, as these are popularly known, in the description of successive rotations.
$(0,\pi /2)$
, respectively, to avoid parametrisation singularities (see, e.g., [Reference Ghosal21], pp. 28–29 and [Reference Murray, Sastry and Zexiang26], p. 33) or gimbal locks, as these are popularly known, in the description of successive rotations.

Figure 1. Faces and vertices of
![]() ${\mathcal{V}_{\mathcal{E}}} \in{\mathcal{E}}$
represented as a cuboid in Euler angles for non-uniform ranges of Euler angles. The numerical values of the limits are listed in Table III.
${\mathcal{V}_{\mathcal{E}}} \in{\mathcal{E}}$
represented as a cuboid in Euler angles for non-uniform ranges of Euler angles. The numerical values of the limits are listed in Table III.
Figure 1 shows the schematic of the corresponding cuboid, that is, an instance of
![]() $\mathcal{V}_{\mathcal{E}}$
. The faces of
$\mathcal{V}_{\mathcal{E}}$
. The faces of
![]() $\mathcal{V}_{\mathcal{E}}$
are termed as
$\mathcal{V}_{\mathcal{E}}$
are termed as
![]() $\mathcal{F}_{({\cdot})}$
, for example, the face associated with
$\mathcal{F}_{({\cdot})}$
, for example, the face associated with
![]() $\gamma = \overline{\gamma }$
is denoted by
$\gamma = \overline{\gamma }$
is denoted by
![]() $\mathcal{F}_{{\overline{\gamma }}}$
. Similarly, the
$\mathcal{F}_{{\overline{\gamma }}}$
. Similarly, the
![]() $\mathcal{F}_{\underline{\gamma }}$
is defined by
$\mathcal{F}_{\underline{\gamma }}$
is defined by
![]() $\gamma ={\underline{\gamma }}$
and so on. The coordinates of the vertices of
$\gamma ={\underline{\gamma }}$
and so on. The coordinates of the vertices of
![]() $\mathcal{V}_{\mathcal{E}}$
are listed in Table II. However, it is known that
$\mathcal{V}_{\mathcal{E}}$
are listed in Table II. However, it is known that
![]() $\mathbb{SO}(3)$
is not Cartesian in nature, since it is neither a linear space, nor does it admit the Euclidean metric, at least in the global sense. Hence, the utility of the schematic in Figure 1 is limited only to a familiar visual representation, beyond which it has no mathematical significance. Nevertheless, from Table II, one can confirm what may be observed in Figure 1 as well, that points in
$\mathbb{SO}(3)$
is not Cartesian in nature, since it is neither a linear space, nor does it admit the Euclidean metric, at least in the global sense. Hence, the utility of the schematic in Figure 1 is limited only to a familiar visual representation, beyond which it has no mathematical significance. Nevertheless, from Table II, one can confirm what may be observed in Figure 1 as well, that points in
![]() $\mathcal{V}_{\mathcal{E}}$
possess central symmetry w.r.t. the origin of
$\mathcal{V}_{\mathcal{E}}$
possess central symmetry w.r.t. the origin of
![]() $\mathcal{E}$
, denoted by
$\mathcal{E}$
, denoted by
![]() $\boldsymbol{o}$
; see, for example, the terminal points of the body-diagonal
$\boldsymbol{o}$
; see, for example, the terminal points of the body-diagonal
![]() $\boldsymbol{p}_1$
and
$\boldsymbol{p}_1$
and
![]() $\boldsymbol{p}_7$
, and their coordinates.
$\boldsymbol{p}_7$
, and their coordinates.
Table II. Vertices of
![]() $\mathcal{V}_{\mathcal{E}}$
, as seen in Fig. 1, in terms of the limits of Euler angles.
$\mathcal{V}_{\mathcal{E}}$
, as seen in Fig. 1, in terms of the limits of Euler angles.


Figure 2. A pictorial depiction of
![]() $\boldsymbol{k}$
, which may be expressed as
$\boldsymbol{k}$
, which may be expressed as
![]() $\boldsymbol{k} = [\cos \zeta \cos \xi, \cos \zeta \sin \xi, \sin \zeta ]^{\top }$
.
$\boldsymbol{k} = [\cos \zeta \cos \xi, \cos \zeta \sin \xi, \sin \zeta ]^{\top }$
.
In order to describe appropriately the subset of
![]() $\mathbb{SO}(3)$
demarcated as
$\mathbb{SO}(3)$
demarcated as
![]() $\mathcal{V}_{\mathcal{E}}$
and to analyse its extent in a physically pertinent manner, it is mapped to the space of Rodrigues parameters,
$\mathcal{V}_{\mathcal{E}}$
and to analyse its extent in a physically pertinent manner, it is mapped to the space of Rodrigues parameters,
![]() $\mathcal{R}$
. This choice of parametrisation is made to take advantage of two facts: (a) Rodrigues parameters are related to the axis-angle representation intrinsically, which affords them physical significance; (b) the Euclidean norm is defined in the neighbourhood of the origin in this space, making it possible to define subsets of
$\mathcal{R}$
. This choice of parametrisation is made to take advantage of two facts: (a) Rodrigues parameters are related to the axis-angle representation intrinsically, which affords them physical significance; (b) the Euclidean norm is defined in the neighbourhood of the origin in this space, making it possible to define subsets of
![]() $\mathbb{SO}(3)$
as spheres centred at the origin (see, e.g., [Reference Nag and Bandyopadhyay11]) and compare their sizes in terms of the radii of these spheres. The details of the mapping are presented below.
$\mathbb{SO}(3)$
as spheres centred at the origin (see, e.g., [Reference Nag and Bandyopadhyay11]) and compare their sizes in terms of the radii of these spheres. The details of the mapping are presented below.
2.1. Mapping of Euler angles into Rodrigues parameters
The relationship between a rotation matrix
![]() $\boldsymbol{R}$
and the vector of Rodrigues parameters,Footnote
4
$\boldsymbol{R}$
and the vector of Rodrigues parameters,Footnote
4
![]() $\boldsymbol{c}=[c_1,c_2,c_3]^{\top } \in{\mathbb{R}}^3$
, is shown in Table 1(a) of [Reference Spring16] and Eq. (204) of [Reference Shuster13]. The derivation is simple and compact; it is presented below for the sake of completeness and to introduce certain notations. It is preceded by a geometric perspective to the Rodrigue’s vector.
$\boldsymbol{c}=[c_1,c_2,c_3]^{\top } \in{\mathbb{R}}^3$
, is shown in Table 1(a) of [Reference Spring16] and Eq. (204) of [Reference Shuster13]. The derivation is simple and compact; it is presented below for the sake of completeness and to introduce certain notations. It is preceded by a geometric perspective to the Rodrigue’s vector.
The description of
![]() $\mathbb{SO}(3)$
via Rodrigues parameters is closely related to a geometric representation due to Euler, who proved that any generic rotation of a rigid body in space is equivalent to a simple rotation about a corresponding axis in space. This leads directly to the so-called axis-angle representation, which is given by the pair
$\mathbb{SO}(3)$
via Rodrigues parameters is closely related to a geometric representation due to Euler, who proved that any generic rotation of a rigid body in space is equivalent to a simple rotation about a corresponding axis in space. This leads directly to the so-called axis-angle representation, which is given by the pair
![]() $(\boldsymbol{k}, \psi )$
, where
$(\boldsymbol{k}, \psi )$
, where
![]() $\boldsymbol{k} \in \mathbb{S}^2$
, that is,
$\boldsymbol{k} \in \mathbb{S}^2$
, that is,
![]() $\boldsymbol{k}$
is a unit vector in
$\boldsymbol{k}$
is a unit vector in
![]() ${\mathbb{R}}^3$
(see Figure 2) which lies along the said axis of rotation, and
${\mathbb{R}}^3$
(see Figure 2) which lies along the said axis of rotation, and
![]() $\psi \in \mathbb{S}^1$
is the corresponding angle, measured about
$\psi \in \mathbb{S}^1$
is the corresponding angle, measured about
![]() $\boldsymbol{k}$
in the CCW sense. A visual depiction of this interpretation of
$\boldsymbol{k}$
in the CCW sense. A visual depiction of this interpretation of
![]() $\mathbb{SO}(3)$
may be found, e.g., in Figure 3 of [Reference Nag and Bandyopadhyay11]. In terms of the axis angle-pair, the Gibbs/Rodrigues vector or the vector of Rodrigues parameters can be expressed explicitly asFootnote
5
$\mathbb{SO}(3)$
may be found, e.g., in Figure 3 of [Reference Nag and Bandyopadhyay11]. In terms of the axis angle-pair, the Gibbs/Rodrigues vector or the vector of Rodrigues parameters can be expressed explicitly asFootnote
5
Considering the norms of both sides of Eq. (4), one arrives at an important result:

Figure 3. Visualisation of subsets of
![]() $\mathbb{SO}(3)$
as spheres in
$\mathbb{SO}(3)$
as spheres in
![]() ${\mathbb{R}}^3$
, as described by Rodrigues parameters. Two sets of Rodrigues vectors are shown, which lie along two unit vectors
${\mathbb{R}}^3$
, as described by Rodrigues parameters. Two sets of Rodrigues vectors are shown, which lie along two unit vectors
![]() $\boldsymbol{k}_1, \boldsymbol{k}_2$
in
$\boldsymbol{k}_1, \boldsymbol{k}_2$
in
![]() ${\mathbb{R}}^3$
and describe rotations through the angles
${\mathbb{R}}^3$
and describe rotations through the angles
![]() $\psi ^{\prime}$
and
$\psi ^{\prime}$
and
![]() $\psi ^{\prime\prime}$
about these.
$\psi ^{\prime\prime}$
about these.
Eqs. (4, 5) show that the Rodrigues vector representing a given rotation is along the axis of rotation and has a magnitude equalling the absolute value of the tangent of half of the angle of rotation. This property leads to a visual representation of the Rodrigues vector, as depicted in Figure 3. It shows two pairs of Rodrigues vectors, namely,
![]() $\{\boldsymbol{c}^{\prime}_1,\boldsymbol{c}^{\prime}_2\}$
, and
$\{\boldsymbol{c}^{\prime}_1,\boldsymbol{c}^{\prime}_2\}$
, and
![]() $\{\boldsymbol{c}^{\prime\prime}_1,\boldsymbol{c}^{\prime\prime}_2\}$
which lie along the axes
$\{\boldsymbol{c}^{\prime\prime}_1,\boldsymbol{c}^{\prime\prime}_2\}$
which lie along the axes
![]() $\boldsymbol{k}_1, \boldsymbol{k}_2$
. The vectors
$\boldsymbol{k}_1, \boldsymbol{k}_2$
. The vectors
![]() $\{\boldsymbol{c}^{\prime}_1, \boldsymbol{c}^{\prime}_2\}$
correspond to rotations through
$\{\boldsymbol{c}^{\prime}_1, \boldsymbol{c}^{\prime}_2\}$
correspond to rotations through
![]() $\psi ^{\prime}$
CCW about
$\psi ^{\prime}$
CCW about
![]() $\boldsymbol{k}_1$
and
$\boldsymbol{k}_1$
and
![]() $\boldsymbol{k}_2$
, respectively, while
$\boldsymbol{k}_2$
, respectively, while
![]() $\{\boldsymbol{c}^{\prime\prime}_1, \boldsymbol{c}^{\prime\prime}_2\}$
describe CCW rotations through
$\{\boldsymbol{c}^{\prime\prime}_1, \boldsymbol{c}^{\prime\prime}_2\}$
describe CCW rotations through
![]() $\psi ^{\prime\prime}$
about the same set of axes. Further, Figure 3 suggests that the elements
$\psi ^{\prime\prime}$
about the same set of axes. Further, Figure 3 suggests that the elements
![]() $\{c_1,c_2,c_3\}$
of
$\{c_1,c_2,c_3\}$
of
![]() $\boldsymbol{c}$
may be interpreted as local coordinates of
$\boldsymbol{c}$
may be interpreted as local coordinates of
![]() ${\mathbb{R}}^3$
around its origin, and subsets of
${\mathbb{R}}^3$
around its origin, and subsets of
![]() $\mathbb{SO}(3)$
can be described by spheres centred at the origin. The radii of these spheres indicate the extent of rotations permissible within the respective subsets, about any axis in space. Obviously, this description is only valid for rotation angles in
$\mathbb{SO}(3)$
can be described by spheres centred at the origin. The radii of these spheres indicate the extent of rotations permissible within the respective subsets, about any axis in space. Obviously, this description is only valid for rotation angles in
![]() $(0, \pi )$
.
$(0, \pi )$
.
An expression for
![]() $\boldsymbol{k}$
corresponding to any
$\boldsymbol{k}$
corresponding to any
![]() $\boldsymbol{R} \in{\mathbb{SO}(3)}$
may be found as
$\boldsymbol{R} \in{\mathbb{SO}(3)}$
may be found as
The operator
![]() $({\cdot})^{\vee }\,:\,{so(3)} \to{\mathbb{R}}^3$
appearing in Eq. (6) produces the so-called vector equivalent of a skew-symmetric matrix; that is,
$({\cdot})^{\vee }\,:\,{so(3)} \to{\mathbb{R}}^3$
appearing in Eq. (6) produces the so-called vector equivalent of a skew-symmetric matrix; that is,
![]() $\boldsymbol{A}\boldsymbol{x} = \boldsymbol{A}^\vee \times \boldsymbol{x}, \forall \boldsymbol{x} \in{\mathbb{R}}^3$
and
$\boldsymbol{A}\boldsymbol{x} = \boldsymbol{A}^\vee \times \boldsymbol{x}, \forall \boldsymbol{x} \in{\mathbb{R}}^3$
and
![]() $\forall \boldsymbol{A} \in{\mathbb{R}}^{3\times 3}$
such that
$\forall \boldsymbol{A} \in{\mathbb{R}}^{3\times 3}$
such that
![]() $\boldsymbol{A}+\boldsymbol{A}^{\top } = \textbf{0} \in{\mathbb{R}}^{3\times 3}$
. Since it has been assumed in the above that
$\boldsymbol{A}+\boldsymbol{A}^{\top } = \textbf{0} \in{\mathbb{R}}^{3\times 3}$
. Since it has been assumed in the above that
![]() $\psi \in (0, \pi )$
, null/full rotations and half-turns about any axis are not included in the following analysis.
$\psi \in (0, \pi )$
, null/full rotations and half-turns about any axis are not included in the following analysis.
Using Eq. (6) in Eq. (4), one obtains
 \begin{align} \boldsymbol{c} & = \frac{(\boldsymbol{R}-\boldsymbol{R}^{\top })^\vee }{2\sin \psi } \tan (\psi /2)\nonumber, \\ & = \frac{(\boldsymbol{R}-\boldsymbol{R}^{\top })^\vee }{4 \cos ^2(\psi /2)}\nonumber, \\ &= \frac{(\boldsymbol{R}-\boldsymbol{R}^{\top })^\vee }{2+2 \cos \psi }. \end{align}
\begin{align} \boldsymbol{c} & = \frac{(\boldsymbol{R}-\boldsymbol{R}^{\top })^\vee }{2\sin \psi } \tan (\psi /2)\nonumber, \\ & = \frac{(\boldsymbol{R}-\boldsymbol{R}^{\top })^\vee }{4 \cos ^2(\psi /2)}\nonumber, \\ &= \frac{(\boldsymbol{R}-\boldsymbol{R}^{\top })^\vee }{2+2 \cos \psi }. \end{align}
Noting that
![]() $\text{tr}({\boldsymbol{R}}) = 1 + 2 \cos \psi$
, an expression for
$\text{tr}({\boldsymbol{R}}) = 1 + 2 \cos \psi$
, an expression for
![]() $\boldsymbol{c}$
is obtained in terms of
$\boldsymbol{c}$
is obtained in terms of
![]() $\boldsymbol{R}$
explicitly:
$\boldsymbol{R}$
explicitly:
For the sake of brevity, an operator
![]() $\stackrel{\frown }{({\cdot})}\,:\,{\mathbb{SO}(3)} \to{\mathbb{R}}^3$
is introduced as follows:
$\stackrel{\frown }{({\cdot})}\,:\,{\mathbb{SO}(3)} \to{\mathbb{R}}^3$
is introduced as follows:
Thus, one can express Eq. (8) compactly as
Furthermore, expressing
![]() $\boldsymbol{R}$
in Eq. (8) as
$\boldsymbol{R}$
in Eq. (8) as
![]() $\boldsymbol{R}_Z(\alpha ) \boldsymbol{R}_Y(\beta ) \boldsymbol{R}_X(\gamma )$
, one can relate the corresponding Rodrigues parameters, denoted by
$\boldsymbol{R}_Z(\alpha ) \boldsymbol{R}_Y(\beta ) \boldsymbol{R}_X(\gamma )$
, one can relate the corresponding Rodrigues parameters, denoted by
![]() $\{d_1, d_2, d_3\}$
, to the Euler angles analytically:
$\{d_1, d_2, d_3\}$
, to the Euler angles analytically:
Considering the equivalent space-fixed rotation matrix
![]() $\boldsymbol{R}^{\prime} =\,\boldsymbol{R}_X(\gamma )\boldsymbol{R}_Y(\beta )\boldsymbol{R}_Z(\alpha )$
, the corresponding Rodrigues parameters are found as
$\boldsymbol{R}^{\prime} =\,\boldsymbol{R}_X(\gamma )\boldsymbol{R}_Y(\beta )\boldsymbol{R}_Z(\alpha )$
, the corresponding Rodrigues parameters are found as
Eqs. (11a–11c) and (12a–12c) are valid iff
![]() $A+B$
and
$A+B$
and
![]() $A-B$
do not vanish, respectively. The real combinations of
$A-B$
do not vanish, respectively. The real combinations of
![]() $\{\alpha, \beta, \gamma \}$
for which these vanish have been studied in Appendix B.
$\{\alpha, \beta, \gamma \}$
for which these vanish have been studied in Appendix B.
The expressions derived above afford the means of mapping
![]() $\mathcal{V}_{\mathcal{E}}$
in Figure 1 to the corresponding solid, namely,
$\mathcal{V}_{\mathcal{E}}$
in Figure 1 to the corresponding solid, namely,
![]() ${\mathcal{V}_{\mathcal{R}}} \in \;{\mathcal{R}}$
, as explained in the following. The bounding surface
${\mathcal{V}_{\mathcal{R}}} \in \;{\mathcal{R}}$
, as explained in the following. The bounding surface
![]() $\mathcal{F}_{({\cdot})}$
is mapped to the surface
$\mathcal{F}_{({\cdot})}$
is mapped to the surface
![]() ${\mathcal{Q}}_{({\cdot})}$
bounding
${\mathcal{Q}}_{({\cdot})}$
bounding
![]() $\mathcal{V}_{\mathcal{R}}$
; e.g.,
$\mathcal{V}_{\mathcal{R}}$
; e.g.,
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
is the mapped surface corresponding to the face
${\mathcal{Q}}_{{\overline{\gamma }}}$
is the mapped surface corresponding to the face
![]() $\mathcal{F}_{{\overline{\gamma }}}$
and so on.
$\mathcal{F}_{{\overline{\gamma }}}$
and so on.
2.2. Mapping of the cuboid
 $\mathcal{V}_{\mathcal{E}}$
in the space of Euler angles
$\mathcal{V}_{\mathcal{E}}$
in the space of Euler angles
 $\mathcal{E}$
into solid regions
$\mathcal{E}$
into solid regions
 $\mathcal{V}_{\mathcal{R}}$
in the space of Rodrigues parameters
$\mathcal{V}_{\mathcal{R}}$
in the space of Rodrigues parameters
 $\mathcal{R}$
$\mathcal{R}$
In order to map
![]() $\mathcal{V}_{\mathcal{E}}$
to
$\mathcal{V}_{\mathcal{E}}$
to
![]() $\mathcal{V}_{\mathcal{R}}$
, its faces are transformed individually. The process is explained in the context of the face
$\mathcal{V}_{\mathcal{R}}$
, its faces are transformed individually. The process is explained in the context of the face
![]() $\mathcal{F}_{{\overline{\gamma }}}$
(see Figure 4a). The remaining faces are treated similarly.
$\mathcal{F}_{{\overline{\gamma }}}$
(see Figure 4a). The remaining faces are treated similarly.

Figure 4. One of the faces of
![]() $\mathcal{V}_{\mathcal{E}}$
and the corresponding surfaces of
$\mathcal{V}_{\mathcal{E}}$
and the corresponding surfaces of
![]() $\mathcal{V}_{\mathcal{R}}$
; (a) face
$\mathcal{V}_{\mathcal{R}}$
; (a) face
![]() $\mathcal{F}_{{\overline{\gamma }}}$
, (b) surface
$\mathcal{F}_{{\overline{\gamma }}}$
, (b) surface
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
,and (c) surface
${\mathcal{Q}}_{{\overline{\gamma }}}$
,and (c) surface
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}^{\prime}$
. The point
${\mathcal{Q}}_{{\overline{\gamma }}}^{\prime}$
. The point
![]() $\boldsymbol{p}$
on the face
$\boldsymbol{p}$
on the face
![]() $\gamma ={\overline{\gamma }}=50^\circ$
corresponds to the parameter values
$\gamma ={\overline{\gamma }}=50^\circ$
corresponds to the parameter values
![]() $\{u,v\}=\{0.8,0.8\}$
(see Eq. (13)).
$\{u,v\}=\{0.8,0.8\}$
(see Eq. (13)).
The face
![]() $\mathcal{F}_{{\overline{\gamma }}}$
is spanned by two linearly independent vectors, given by
$\mathcal{F}_{{\overline{\gamma }}}$
is spanned by two linearly independent vectors, given by
![]() $\boldsymbol{a}_1 = \boldsymbol{p}_8 - \boldsymbol{p}_5$
, and
$\boldsymbol{a}_1 = \boldsymbol{p}_8 - \boldsymbol{p}_5$
, and
![]() $\boldsymbol{a}_2 = \boldsymbol{p}_6 - \boldsymbol{p}_5$
, as shown in Figure 4a. Any point on this face, say,
$\boldsymbol{a}_2 = \boldsymbol{p}_6 - \boldsymbol{p}_5$
, as shown in Figure 4a. Any point on this face, say,
![]() $\boldsymbol{p}=[\alpha, \beta, \gamma ]^{\top }$
, may be represented in terms of the pair of parameters
$\boldsymbol{p}=[\alpha, \beta, \gamma ]^{\top }$
, may be represented in terms of the pair of parameters
![]() $\{u,v\}$
as
$\{u,v\}$
as
Using Eq. (13) in Eq. (11), one obtains a
![]() $\{u,v\}$
parametrisation of the desired surface in
$\{u,v\}$
parametrisation of the desired surface in
![]() $\mathcal{R}$
, denoted by
$\mathcal{R}$
, denoted by
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
, using the Z-Y-X sequence of Euler angles. This surface has been visualised in Figure 4b. Similarly, a combination of Eq. (13) and Eq. (12) results in the surface, denoted by
${\mathcal{Q}}_{{\overline{\gamma }}}$
, using the Z-Y-X sequence of Euler angles. This surface has been visualised in Figure 4b. Similarly, a combination of Eq. (13) and Eq. (12) results in the surface, denoted by
![]() ${\mathcal{Q}}^{\prime}_{{\overline{\gamma }}}$
, corresponding to the X-Y-Z sequence, as shown in Figure 4c.
${\mathcal{Q}}^{\prime}_{{\overline{\gamma }}}$
, corresponding to the X-Y-Z sequence, as shown in Figure 4c.
The same procedure is followed for the remaining five faces in both conventions, whence they enclose two different instances of
![]() $\mathcal{V}_{\mathcal{R}}$
, denoted by
$\mathcal{V}_{\mathcal{R}}$
, denoted by
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
, respectively. These may be seen individually in Figures 6a, 6b, and together in Figure 6c. The corresponding instances of
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
, respectively. These may be seen individually in Figures 6a, 6b, and together in Figure 6c. The corresponding instances of
![]() $\mathcal{V}_{\mathcal{R}}$
for uniform symmetric ranges of Euler angles are shown in Figures 5a, 5b, and 5c, respectively. The coordinates of the points
$\mathcal{V}_{\mathcal{R}}$
for uniform symmetric ranges of Euler angles are shown in Figures 5a, 5b, and 5c, respectively. The coordinates of the points
![]() $\boldsymbol{p}_i$
are listed in Table II, and their numerical values are tabulated in Table III. The coordinates of the vertices
$\boldsymbol{p}_i$
are listed in Table II, and their numerical values are tabulated in Table III. The coordinates of the vertices
![]() $\boldsymbol{m}_i$
are obtained by using Eq. (13) and its counterparts for the other faces of
$\boldsymbol{m}_i$
are obtained by using Eq. (13) and its counterparts for the other faces of
![]() $\mathcal{V}_{\mathcal{E}}$
in Eqs. (11). These are shown in Figures 5a–5c. Similarly, the vertices
$\mathcal{V}_{\mathcal{E}}$
in Eqs. (11). These are shown in Figures 5a–5c. Similarly, the vertices
![]() $\boldsymbol{n}_i$
are obtained via Eqs. (12), and these are shown in Figures 6a–6c.
$\boldsymbol{n}_i$
are obtained via Eqs. (12), and these are shown in Figures 6a–6c.
Table III. Uniform and non-uniform ranges of Euler angles used in this article.


Figure 5. Solids
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
corresponding to uniform symmetric ranges of Euler angles
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
corresponding to uniform symmetric ranges of Euler angles
![]() $\alpha, \beta, \gamma \in [-30^\circ, 30^\circ ]$
(see Table III).
$\alpha, \beta, \gamma \in [-30^\circ, 30^\circ ]$
(see Table III).

Figure 6. Solids
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
corresponding to non-uniform symmetric ranges of Euler angles
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
corresponding to non-uniform symmetric ranges of Euler angles
![]() $\{\alpha, \beta, \gamma \}\in [-30^\circ, 30^\circ ]\times [-40^\circ, 40^\circ ]\times [-50^\circ, 50^\circ ]$
(refer to Table III).
$\{\alpha, \beta, \gamma \}\in [-30^\circ, 30^\circ ]\times [-40^\circ, 40^\circ ]\times [-50^\circ, 50^\circ ]$
(refer to Table III).
2.3. Relations between
 $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
 $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
for symmetric ranges of Euler angles
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
for symmetric ranges of Euler angles
If the limits of Euler angles are chosen in a symmetric manner, then it is easy to see that the pairs of vertices of
![]() $\mathcal{V}_{\mathcal{E}}$
delimiting each of its body-diagonal maps to their respective inverses in
$\mathcal{V}_{\mathcal{E}}$
delimiting each of its body-diagonal maps to their respective inverses in
![]() $\mathbb{SO}(3)$
; that is., if the line segment joining the vertices
$\mathbb{SO}(3)$
; that is., if the line segment joining the vertices
![]() $\boldsymbol{p}_i$
and
$\boldsymbol{p}_i$
and
![]() $\boldsymbol{p}_j$
,
$\boldsymbol{p}_j$
,
![]() $i\ne j$
constitutes a body diagonal, and the corresponding rotation matrices are given by
$i\ne j$
constitutes a body diagonal, and the corresponding rotation matrices are given by
![]() $\boldsymbol{R}_{\boldsymbol{p}_i}$
and
$\boldsymbol{R}_{\boldsymbol{p}_i}$
and
![]() $\boldsymbol{R}^{\prime}_{\boldsymbol{p}_j}$
, respectively, then
$\boldsymbol{R}^{\prime}_{\boldsymbol{p}_j}$
, respectively, then
![]() $\boldsymbol{R}^{\prime}_{\boldsymbol{p}_j} = \boldsymbol{R}^{\top }_{\boldsymbol{p}_i}$
, where
$\boldsymbol{R}^{\prime}_{\boldsymbol{p}_j} = \boldsymbol{R}^{\top }_{\boldsymbol{p}_i}$
, where
![]() $\boldsymbol{R}^{\prime}$
denotes the space-fixed counterpart of any body-fixed rotation matrix
$\boldsymbol{R}^{\prime}$
denotes the space-fixed counterpart of any body-fixed rotation matrix
![]() $\boldsymbol{R}$
. This relation is a consequence of the intrinsic central symmetry among the points in
$\boldsymbol{R}$
. This relation is a consequence of the intrinsic central symmetry among the points in
![]() $\mathcal{V}_{\mathcal{E}}$
. Obviously, in this case, this symmetry must be interpreted in the context of the group operation of
$\mathcal{V}_{\mathcal{E}}$
. Obviously, in this case, this symmetry must be interpreted in the context of the group operation of
![]() $\mathbb{SO}(3)$
; that is, matrix multiplications, since
$\mathbb{SO}(3)$
; that is, matrix multiplications, since
![]() $\boldsymbol{R}_{\boldsymbol{p}_i} \boldsymbol{R}^{\prime}_{\boldsymbol{p}_j} = \boldsymbol{I}_{3\times 3}$
,
$\boldsymbol{R}_{\boldsymbol{p}_i} \boldsymbol{R}^{\prime}_{\boldsymbol{p}_j} = \boldsymbol{I}_{3\times 3}$
,
![]() $\boldsymbol{I}_{3\times 3} = \operatorname{diag}(1,1,1)$
being the multiplicative identity in
$\boldsymbol{I}_{3\times 3} = \operatorname{diag}(1,1,1)$
being the multiplicative identity in
![]() $\mathbb{SO}(3)$
. In the following, this symmetry is demonstrated in the context of the body diagonal connecting the vertices
$\mathbb{SO}(3)$
. In the following, this symmetry is demonstrated in the context of the body diagonal connecting the vertices
![]() $\boldsymbol{p}_3$
and
$\boldsymbol{p}_3$
and
![]() $\boldsymbol{p}_5$
(see Figure 1).
$\boldsymbol{p}_5$
(see Figure 1).
Given the coordinates of
![]() $\boldsymbol{p}_3,\boldsymbol{p}_5$
in Table II, one can write
$\boldsymbol{p}_3,\boldsymbol{p}_5$
in Table II, one can write
Further, the matrix
![]() $\boldsymbol{R}^{\prime}_{\boldsymbol{p}_5}$
may be obtained as
$\boldsymbol{R}^{\prime}_{\boldsymbol{p}_5}$
may be obtained as
 \begin{align} \boldsymbol{R}^{\prime}_{\boldsymbol{p}_5} & =\boldsymbol{R}_X^{\top }(-{\overline{\gamma }})\boldsymbol{R}_Y^{\top }(-{\underline{\beta }})\boldsymbol{R}_Z^{\top }(-{\underline{\alpha }}),\nonumber \\ & =\boldsymbol{R}_X^{\top }({\underline{\gamma }})\boldsymbol{R}_Y^{\top }({\overline{\beta }})\boldsymbol{R}_Z^{\top }({\overline{\alpha }}), \quad \text{since ${\overline{\alpha }} = -{\underline{\alpha }}$ and so on, as per Eq. (3)};\nonumber \\ \Rightarrow \boldsymbol{R}^{\prime}_{\boldsymbol{p}_5} & = \left (\boldsymbol{R}_Z({\overline{\alpha }})\boldsymbol{R}_Y({\overline{\beta }})\boldsymbol{R}_X({\underline{\gamma }})\right )^{\top }, \nonumber \\ & = \boldsymbol{R}_{\boldsymbol{p}_3}^{\top }, \ \text{following Eq. (14a)};\nonumber \\ \Rightarrow \boldsymbol{R}^{\top }_{\boldsymbol{p}_3} & = \boldsymbol{R}^{\prime}_{\boldsymbol{p}_5}. \end{align}
\begin{align} \boldsymbol{R}^{\prime}_{\boldsymbol{p}_5} & =\boldsymbol{R}_X^{\top }(-{\overline{\gamma }})\boldsymbol{R}_Y^{\top }(-{\underline{\beta }})\boldsymbol{R}_Z^{\top }(-{\underline{\alpha }}),\nonumber \\ & =\boldsymbol{R}_X^{\top }({\underline{\gamma }})\boldsymbol{R}_Y^{\top }({\overline{\beta }})\boldsymbol{R}_Z^{\top }({\overline{\alpha }}), \quad \text{since ${\overline{\alpha }} = -{\underline{\alpha }}$ and so on, as per Eq. (3)};\nonumber \\ \Rightarrow \boldsymbol{R}^{\prime}_{\boldsymbol{p}_5} & = \left (\boldsymbol{R}_Z({\overline{\alpha }})\boldsymbol{R}_Y({\overline{\beta }})\boldsymbol{R}_X({\underline{\gamma }})\right )^{\top }, \nonumber \\ & = \boldsymbol{R}_{\boldsymbol{p}_3}^{\top }, \ \text{following Eq. (14a)};\nonumber \\ \Rightarrow \boldsymbol{R}^{\top }_{\boldsymbol{p}_3} & = \boldsymbol{R}^{\prime}_{\boldsymbol{p}_5}. \end{align}
This symmetry persists in
![]() $\mathcal{R}$
. The images of
$\mathcal{R}$
. The images of
![]() $\boldsymbol{p}_i\in{\mathcal{V}_{\mathcal{E}}}$
in
$\boldsymbol{p}_i\in{\mathcal{V}_{\mathcal{E}}}$
in
![]() $\mathcal{R}$
are the points
$\mathcal{R}$
are the points
![]() $\boldsymbol{m}_i = \stackrel{\frown }{\boldsymbol{R}}_{\boldsymbol{p}_i} \in{\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)}$
and
$\boldsymbol{m}_i = \stackrel{\frown }{\boldsymbol{R}}_{\boldsymbol{p}_i} \in{\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)}$
and
![]() $\boldsymbol{n}_i = \stackrel{\frown }{\boldsymbol{R}^{\prime}}_{\boldsymbol{p}_i} \in{\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)}$
, respectively,
$\boldsymbol{n}_i = \stackrel{\frown }{\boldsymbol{R}^{\prime}}_{\boldsymbol{p}_i} \in{\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)}$
, respectively,
![]() $i = 1,\ldots, 8$
. Therefore, one can write
$i = 1,\ldots, 8$
. Therefore, one can write
Considering Eq. (15), this becomes
This relation can be observed numerically in Table IV, wherein the corresponding entries have been presented in bold fonts. Similarly, the point
![]() $\boldsymbol{n}_j$
has been placed on the same row as the corresponding
$\boldsymbol{n}_j$
has been placed on the same row as the corresponding
![]() $\boldsymbol{m}_i$
. From these derivations and discussions, it may be concluded that for symmetric ranges of Euler angles, points in
$\boldsymbol{m}_i$
. From these derivations and discussions, it may be concluded that for symmetric ranges of Euler angles, points in
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
bear central symmetry with respect to the origin of
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
bear central symmetry with respect to the origin of
![]() $\mathcal{R}$
(i.e., point corresponding to zero rotation) with the corresponding points in
$\mathcal{R}$
(i.e., point corresponding to zero rotation) with the corresponding points in
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
.
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
.
3. Identification of the largest spheres centred at the origin and contained within
 $\mathcal{V}_{\mathcal{R}}$
$\mathcal{V}_{\mathcal{R}}$
The instances of
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
obtained by mapping
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
obtained by mapping
![]() $\mathcal{V}_{\mathcal{E}}$
into
$\mathcal{V}_{\mathcal{E}}$
into
![]() $\mathcal{R}$
have complicated shapes, as seen in Figure 5, and Figure 6, respectively. Most importantly, these are seen to be non-convex solids, and hence, not favourable for a convenient yet accurate description of the orientation workspace. Spherical shapes are preferred for this purpose given the obvious advantages they provide, in addition to being convex: (a) spatial homogeneity – a sphere extends to identical extents in all spatial directions and (b) ease of point classification – any given point in
$\mathcal{R}$
have complicated shapes, as seen in Figure 5, and Figure 6, respectively. Most importantly, these are seen to be non-convex solids, and hence, not favourable for a convenient yet accurate description of the orientation workspace. Spherical shapes are preferred for this purpose given the obvious advantages they provide, in addition to being convex: (a) spatial homogeneity – a sphere extends to identical extents in all spatial directions and (b) ease of point classification – any given point in
![]() $\mathbb{SO}(3)$
may be trivially identified as being “inside” or “outside” or “on” such a sphere, based simply on a comparison of the distance of the point from the centre of the sphere (the origin, in the present case) with the radius of the said sphere.Footnote
6
$\mathbb{SO}(3)$
may be trivially identified as being “inside” or “outside” or “on” such a sphere, based simply on a comparison of the distance of the point from the centre of the sphere (the origin, in the present case) with the radius of the said sphere.Footnote
6
Naturally, in addition to making sure that the desired sphere is centred at the origin and contained fully inside
![]() $\mathcal{V}_{\mathcal{R}}$
, it is of interest to maximise its radius, so as to maximise the set of accessible orientations within the said sphere. Such a sphere would obviously be tangent to at least one of the bounding surfaces of
$\mathcal{V}_{\mathcal{R}}$
, it is of interest to maximise its radius, so as to maximise the set of accessible orientations within the said sphere. Such a sphere would obviously be tangent to at least one of the bounding surfaces of
![]() $\mathcal{V}_{\mathcal{R}}$
. Therefore, the desired sphere may be identified in two steps: (a) finding all the spheres tangent to each of the bounding surfaces individually and (b) choosing the smallest among them (since the larger ones may intersect one or more boundary surfaces at other points). The computations involved in step (a) are explained below in the context of the surface
$\mathcal{V}_{\mathcal{R}}$
. Therefore, the desired sphere may be identified in two steps: (a) finding all the spheres tangent to each of the bounding surfaces individually and (b) choosing the smallest among them (since the larger ones may intersect one or more boundary surfaces at other points). The computations involved in step (a) are explained below in the context of the surface
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
shown in Figure 4.
${\mathcal{Q}}_{{\overline{\gamma }}}$
shown in Figure 4.
Let, the desired sphere be denoted by
![]() $\mathcal{S}$
and have the radius
$\mathcal{S}$
and have the radius
![]() $r$
. Obviously, the radius represents a critical value of the distance of the surface from the centre of
$r$
. Obviously, the radius represents a critical value of the distance of the surface from the centre of
![]() $\mathcal{S}$
, that is, the origin. An arbitrary point on the surface may be located by the corresponding Rodrigues parameters
$\mathcal{S}$
, that is, the origin. An arbitrary point on the surface may be located by the corresponding Rodrigues parameters
![]() $\{d_1, d_2, d_3\}$
, as per Eq. (11). As shown in Eq. (13) (in the context of a different face of
$\{d_1, d_2, d_3\}$
, as per Eq. (11). As shown in Eq. (13) (in the context of a different face of
![]() $\mathcal{V}_{\mathcal{E}}$
), these coordinates may be expressed explicitly in terms of the surface parameters,
$\mathcal{V}_{\mathcal{E}}$
), these coordinates may be expressed explicitly in terms of the surface parameters,
![]() $\{u,v\}$
:
$\{u,v\}$
:
Eqs. (17a–17c) is valid iff
![]() $A^{\prime}+B^{\prime} \ne 0$
and that the same has been discussed further in Appendix B. Therefore, the task reduces to finding the critical points of the squared distance function from the origin, which is given by
$A^{\prime}+B^{\prime} \ne 0$
and that the same has been discussed further in Appendix B. Therefore, the task reduces to finding the critical points of the squared distance function from the origin, which is given by
From Eq. (5),
![]() $r^2$
equals
$r^2$
equals
![]() $\tan ^2\frac{\phi }{2}$
, where
$\tan ^2\frac{\phi }{2}$
, where
![]() $\phi \in (0, \pi )$
denotes the critical value of the rotation that may be achieved. In view of the expressions of
$\phi \in (0, \pi )$
denotes the critical value of the rotation that may be achieved. In view of the expressions of
![]() $d_i$
in terms of
$d_i$
in terms of
![]() $\{u,v\}$
,
$\{u,v\}$
,
![]() $r^2$
may be written explicitly in terms of
$r^2$
may be written explicitly in terms of
![]() $\{u,v\}$
, leading to the formulation of the following optimisation problem:
$\{u,v\}$
, leading to the formulation of the following optimisation problem:
 \begin{align} \begin{aligned} &\underset{\{u,v\}}{\text{Maximise}} & & f(u,v)= r^2, \\ &\text{subject to} & & u,v \in [0,1]. \end{aligned} \\[-4pt]\nonumber \end{align}
\begin{align} \begin{aligned} &\underset{\{u,v\}}{\text{Maximise}} & & f(u,v)= r^2, \\ &\text{subject to} & & u,v \in [0,1]. \end{aligned} \\[-4pt]\nonumber \end{align}
Using the constrained Lagrangian formulation to incorporate the boundary constraints, the objective function becomes
where
![]() $\lambda _i,i=1,\dots, 4$
are the Lagrange multipliers and
$\lambda _i,i=1,\dots, 4$
are the Lagrange multipliers and
![]() $s_j,j=1,\dots, 4$
, the slack variables (see [Reference Deb28], p. 361). Setting the partial derivatives of
$s_j,j=1,\dots, 4$
, the slack variables (see [Reference Deb28], p. 361). Setting the partial derivatives of
![]() $\mathcal{L}$
w.r.t.
$\mathcal{L}$
w.r.t.
![]() $\{u,v,\lambda _i,s_j\}$
to zero, the corresponding equations are obtained as follows:
$\{u,v,\lambda _i,s_j\}$
to zero, the corresponding equations are obtained as follows:
 \begin{align} &\frac{\partial{\mathcal{L}}}{\partial \lambda _1}:= s_1-u=0, \quad \frac{\partial{\mathcal{L}}}{\partial \lambda _2}:= 1-s_2-u=0,\quad \frac{\partial{\mathcal{L}}}{\partial \lambda _3}:= s_3-v=0,\quad \nonumber \\ &\frac{\partial{\mathcal{L}}}{\partial \lambda _4}:=1-s_4-v=0, \\[-3pt]\nonumber \end{align}
\begin{align} &\frac{\partial{\mathcal{L}}}{\partial \lambda _1}:= s_1-u=0, \quad \frac{\partial{\mathcal{L}}}{\partial \lambda _2}:= 1-s_2-u=0,\quad \frac{\partial{\mathcal{L}}}{\partial \lambda _3}:= s_3-v=0,\quad \nonumber \\ &\frac{\partial{\mathcal{L}}}{\partial \lambda _4}:=1-s_4-v=0, \\[-3pt]\nonumber \end{align}
Eq. (21d) shows that
![]() $\lambda _i = 0, i=1,\dots, 4$
. Therefore, Eqs. (21a, 21b) reduce to two transcendental equations, respectively:
$\lambda _i = 0, i=1,\dots, 4$
. Therefore, Eqs. (21a, 21b) reduce to two transcendental equations, respectively:
The real solutions of
![]() $\{u,v\}$
obtained from Eqs. (22a, 22b) are used in Eqs. (21c) to obtain the corresponding values of
$\{u,v\}$
obtained from Eqs. (22a, 22b) are used in Eqs. (21c) to obtain the corresponding values of
![]() $s_j$
. If
$s_j$
. If
![]() $s_j \gt 0\; \forall j$
, then the solutions
$s_j \gt 0\; \forall j$
, then the solutions
![]() $\{u,v\}$
are deemed feasible. If
$\{u,v\}$
are deemed feasible. If
![]() $s_j=0$
for some
$s_j=0$
for some
![]() $j$
, then the critical point lies on the corresponding boundary of the domain of
$j$
, then the critical point lies on the corresponding boundary of the domain of
![]() $\{u,v\}$
. The solutions leading to
$\{u,v\}$
. The solutions leading to
![]() $s_j\lt 0$
for any
$s_j\lt 0$
for any
![]() $j$
are infeasible. Thus, the above method of solving a constrained optimisation problem is seen to be equivalent to the solutions of the corresponding unconstrained problem, followed by imposing the boundary constraints on the real solutions to identify the feasible ones among those.
$j$
are infeasible. Thus, the above method of solving a constrained optimisation problem is seen to be equivalent to the solutions of the corresponding unconstrained problem, followed by imposing the boundary constraints on the real solutions to identify the feasible ones among those.
The critical points are identified as follows. Expressions of
![]() $f_u(u,v)$
and
$f_u(u,v)$
and
![]() $f_v(u,v)$
are quoted below.
$f_v(u,v)$
are quoted below.
Since
![]() ${\underline{\alpha }},{\underline{\beta }}$
cannot vanish, the larger factors appearing in the numerators of
${\underline{\alpha }},{\underline{\beta }}$
cannot vanish, the larger factors appearing in the numerators of
![]() $f_u(u,v)$
and
$f_u(u,v)$
and
![]() $f_v(u,v)$
form a system of linear equations in
$f_v(u,v)$
form a system of linear equations in
![]() $\{\sin u^{\prime\prime},\cos u^{\prime\prime}\}$
, which may be written in the form:
$\{\sin u^{\prime\prime},\cos u^{\prime\prime}\}$
, which may be written in the form:
Given that
![]() ${\| \boldsymbol{x}\|} = 1\; \forall u^{\prime\prime}\in{\mathbb{R}}$
, for Eq. (24a) to be consistent, one must have
${\| \boldsymbol{x}\|} = 1\; \forall u^{\prime\prime}\in{\mathbb{R}}$
, for Eq. (24a) to be consistent, one must have
![]() $\det (\boldsymbol{A}) = 0$
and
$\det (\boldsymbol{A}) = 0$
and
![]() $\boldsymbol{x} \in \mathcal{N}(\boldsymbol{A})$
, where
$\boldsymbol{x} \in \mathcal{N}(\boldsymbol{A})$
, where
![]() $\mathcal{N}({\cdot})$
denotes the nullspace of a matrix. The determinantal equation may be expanded as
$\mathcal{N}({\cdot})$
denotes the nullspace of a matrix. The determinantal equation may be expanded as
The solution of Eq. (25) is obtained as
Similarly, it is found that
Thus,
![]() $\{u,v\}=\{1/2,1/2\}$
is the unique critical point, which is also feasible, as can be verified trivially. Also, at this point, one can verify that
$\{u,v\}=\{1/2,1/2\}$
is the unique critical point, which is also feasible, as can be verified trivially. Also, at this point, one can verify that
which bolsters the validity of the solution.
The value of the objective function at this critical point is computed from Eqs. (17a–17c, 18, 19) as
Corresponding to the pair of solutions above, there are two points of tangency between the maximal sphere and two of the surfaces delimiting
![]() $\mathcal{V}_{\mathcal{R}}$
, namely,
$\mathcal{V}_{\mathcal{R}}$
, namely,
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
, and
${\mathcal{Q}}_{{\overline{\gamma }}}$
, and
![]() ${\mathcal{Q}}_{{\underline{\gamma }}}$
. The locations of these points, respectively, are obtained from Eqs. (11) as
${\mathcal{Q}}_{{\underline{\gamma }}}$
. The locations of these points, respectively, are obtained from Eqs. (11) as
These points of tangency and parts of the corresponding surfaces are shown in Figures 7a and 7b, respectively.

Figure 7. Spheres tangent to (a)
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
and (b)
${\mathcal{Q}}_{{\overline{\gamma }}}$
and (b)
![]() ${\mathcal{Q}}_{{\underline{\gamma }}}$
of
${\mathcal{Q}}_{{\underline{\gamma }}}$
of
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
corresponding to the faces
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
corresponding to the faces
![]() $\mathcal{F}_{{\overline{\gamma }}}$
and
$\mathcal{F}_{{\overline{\gamma }}}$
and
![]() $\mathcal{F}_{{\underline{\gamma }}}$
, respectively (refer to Table III for corresponding numeric details).
$\mathcal{F}_{{\underline{\gamma }}}$
, respectively (refer to Table III for corresponding numeric details).
The above computations need to be repeated only for two of the remaining four surfaces due to the symmetry in the limits of Euler angles. It may be verified that the surfaces
![]() ${\mathcal{Q}}_{{\overline{\beta }}}$
and
${\mathcal{Q}}_{{\overline{\beta }}}$
and
![]() ${\mathcal{Q}}_{{\overline{\alpha }}}$
are tangent to two spheres, with radii
${\mathcal{Q}}_{{\overline{\alpha }}}$
are tangent to two spheres, with radii
![]() $\left |\tan \frac{{\overline{\beta }}}{2}\right |$
and
$\left |\tan \frac{{\overline{\beta }}}{2}\right |$
and
![]() $\left |\tan \frac{{\overline{\alpha }}}{2}\right |$
, respectively. Finally, taking all of these into consideration, the largest sphere (
$\left |\tan \frac{{\overline{\alpha }}}{2}\right |$
, respectively. Finally, taking all of these into consideration, the largest sphere (
![]() $\overline{{\mathcal{S}}}$
) that fits completely inside
$\overline{{\mathcal{S}}}$
) that fits completely inside
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
is found to be the one with the following radius (
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
is found to be the one with the following radius (
![]() $\overline{r}$
):
$\overline{r}$
):
 \begin{align} {\overline{r}} = \min \left \{ \left |\tan \frac{{\overline{\alpha }}}{2}\right |, \left |\tan \frac{{\overline{\beta }}}{2}\right |, \left |\tan \frac{{\overline{\gamma }}}{2}\right | \right \}. \end{align}
\begin{align} {\overline{r}} = \min \left \{ \left |\tan \frac{{\overline{\alpha }}}{2}\right |, \left |\tan \frac{{\overline{\beta }}}{2}\right |, \left |\tan \frac{{\overline{\gamma }}}{2}\right | \right \}. \end{align}
The sphere
![]() $\overline{{\mathcal{S}}}$
with radius
$\overline{{\mathcal{S}}}$
with radius
![]() $\overline{r}$
in
$\overline{r}$
in
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
are shown in Figures 8a and 8b, respectively. Due to the central symmetry (as explained in Section 2.3) between the vertices of
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
are shown in Figures 8a and 8b, respectively. Due to the central symmetry (as explained in Section 2.3) between the vertices of
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
,
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
,
![]() $\overline{{\mathcal{S}}}$
is tangent to the surfaces
$\overline{{\mathcal{S}}}$
is tangent to the surfaces
![]() ${\mathcal{Q}}_{{\overline{\alpha }}}$
and
${\mathcal{Q}}_{{\overline{\alpha }}}$
and
![]() ${\mathcal{Q}}_{{\underline{\alpha }}}$
in both cases.
${\mathcal{Q}}_{{\underline{\alpha }}}$
in both cases.

Figure 8. Sphere
![]() $\overline{{\mathcal{S}}}$
inside
$\overline{{\mathcal{S}}}$
inside
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
corresponding to the non-uniform ranges of Euler angles
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
corresponding to the non-uniform ranges of Euler angles
![]() $\{\alpha, \beta, \gamma \}\in [-30^\circ, 30^\circ ]\times [-40^\circ, 40^\circ ]\times [-50^\circ, 50^\circ ]$
(refer to Table III). In each case,
$\{\alpha, \beta, \gamma \}\in [-30^\circ, 30^\circ ]\times [-40^\circ, 40^\circ ]\times [-50^\circ, 50^\circ ]$
(refer to Table III). In each case,
![]() $\overline{{\mathcal{S}}}$
is tangent to the surface corresponding to
$\overline{{\mathcal{S}}}$
is tangent to the surface corresponding to
![]() $\alpha =30^\circ$
.
$\alpha =30^\circ$
.
The surfaces
![]() ${\mathcal{Q}}_{{\overline{\alpha }}}$
, etc., are derived in their implicit forms and characterised geometrically in the following section .
${\mathcal{Q}}_{{\overline{\alpha }}}$
, etc., are derived in their implicit forms and characterised geometrically in the following section .
4. Geometric Characterisation of
 ${\mathcal{Q}}_{\overline{\gamma}}$
,
${\mathcal{Q}}_{\overline{\gamma}}$
,
 ${\mathcal{Q}}_{\underline{\gamma}}$
, etc
${\mathcal{Q}}_{\underline{\gamma}}$
, etc
The parametric forms of the surfaces
![]() ${\mathcal{Q}}_{{\overline{\alpha }}}$
, etc., accomplish the main goal of this work, namely, the identification of the largest contained sphere
${\mathcal{Q}}_{{\overline{\alpha }}}$
, etc., accomplish the main goal of this work, namely, the identification of the largest contained sphere
![]() $\overline{{\mathcal{S}}}$
analytically. However, it is of interest to study these surfaces further to understand their geometric natures. This has been presented in the following by first converting these surfaces to their respective implicit forms, followed by a comprehensive characterisation. It is found that each of the surfaces
$\overline{{\mathcal{S}}}$
analytically. However, it is of interest to study these surfaces further to understand their geometric natures. This has been presented in the following by first converting these surfaces to their respective implicit forms, followed by a comprehensive characterisation. It is found that each of the surfaces
![]() ${\mathcal{Q}}_{{\overline{\alpha }}}$
, etc., are quadrics in nature; more precisely, they form hyperboloids of one sheet. The largest contained sphere is computed in this new geometric framework as well, which serves as an alternative derivation as well as a formal confirmation of the results obtained in Section 3.
${\mathcal{Q}}_{{\overline{\alpha }}}$
, etc., are quadrics in nature; more precisely, they form hyperboloids of one sheet. The largest contained sphere is computed in this new geometric framework as well, which serves as an alternative derivation as well as a formal confirmation of the results obtained in Section 3.
4.1. Derivation of the implicit forms of the bounding surfaces
 ${\mathcal{Q}}_{\overline{\gamma}}$
,
${\mathcal{Q}}_{\overline{\gamma}}$
,
 ${\mathcal{Q}}_{\underline{\gamma}}$
, etc
${\mathcal{Q}}_{\underline{\gamma}}$
, etc
The trigonometric parametrisation of the surfaces
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
,
${\mathcal{Q}}_{{\overline{\gamma }}}$
,
![]() ${\mathcal{Q}}_{{\underline{\gamma }}}$
, etc., (presented in Eqs. (17a-17c)) makes it difficult to understand their geometric nature. Hence, these trigonometric functions are converted to their algebraic counterparts in the variables
${\mathcal{Q}}_{{\underline{\gamma }}}$
, etc., (presented in Eqs. (17a-17c)) makes it difficult to understand their geometric nature. Hence, these trigonometric functions are converted to their algebraic counterparts in the variables
![]() $\{{t_\alpha },{t_\beta },{t_\gamma }\}$
using the standard tangent of half angle transformations:
$\{{t_\alpha },{t_\beta },{t_\gamma }\}$
using the standard tangent of half angle transformations:
Further, two new parameters, namely,
![]() $\{{\tilde{u}},{\tilde{v}}\}$
, are introduced to describe each of the surfaces. For example, the surface
$\{{\tilde{u}},{\tilde{v}}\}$
, are introduced to describe each of the surfaces. For example, the surface
![]() ${\mathcal{Q}}_{{\overline{\alpha }}}$
is re-parametrised as
${\mathcal{Q}}_{{\overline{\alpha }}}$
is re-parametrised as
Similarly,
![]() ${\mathcal{Q}}_{{\overline{\beta }}}$
,
${\mathcal{Q}}_{{\overline{\beta }}}$
,
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
may be described by, respectively:
${\mathcal{Q}}_{{\overline{\gamma }}}$
may be described by, respectively:
Parametrisation of
![]() ${\mathcal{Q}}_{{\underline{\alpha }}}$
,
${\mathcal{Q}}_{{\underline{\alpha }}}$
,
![]() ${\mathcal{Q}}_{{\underline{\beta }}}$
and
${\mathcal{Q}}_{{\underline{\beta }}}$
and
![]() ${\mathcal{Q}}_{{\underline{\gamma }}}$
in terms of
${\mathcal{Q}}_{{\underline{\gamma }}}$
in terms of
![]() $\tilde{u}$
and
$\tilde{u}$
and
![]() $\tilde{v}$
may be performed in an analogous manner. Derivation of the implicit forms of these surfaces requires the elimination of the parameters
$\tilde{v}$
may be performed in an analogous manner. Derivation of the implicit forms of these surfaces requires the elimination of the parameters
![]() $\tilde{u}$
,
$\tilde{u}$
,
![]() $\tilde{v}$
from the parametric forms of these surfaces. The process is described below in the context of the surface
$\tilde{v}$
from the parametric forms of these surfaces. The process is described below in the context of the surface
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
, using the Z-Y-X sequence of Euler angles.
${\mathcal{Q}}_{{\overline{\gamma }}}$
, using the Z-Y-X sequence of Euler angles.
Using Eqs. (34), and (36b) in Eqs. (11), the Rodrigues parameters
![]() $\{d_1,d_2,d_3\}$
are expressed in terms of
$\{d_1,d_2,d_3\}$
are expressed in terms of
![]() $\tilde{u}$
,
$\tilde{u}$
,
![]() $\tilde{v}$
:
$\tilde{v}$
:
In the following, it would be assumed that
![]() $D \ne 0$
, which would be verified later (see Section 4.4).
$D \ne 0$
, which would be verified later (see Section 4.4).
Eq. (37a–37c) is bilinear in
![]() $\{{\tilde{u}},{\tilde{v}}\}$
; that is, they contain the following monomials
Footnote
7
(see, e.g., [Reference Cox, Little and O’Shea29], pp. 1–2):
$\{{\tilde{u}},{\tilde{v}}\}$
; that is, they contain the following monomials
Footnote
7
(see, e.g., [Reference Cox, Little and O’Shea29], pp. 1–2):
![]() $\{{\tilde{u}},{\tilde{v}},{\tilde{u}}{\tilde{v}}\}$
. These equations may be organised into the following linear system:
$\{{\tilde{u}},{\tilde{v}},{\tilde{u}}{\tilde{v}}\}$
. These equations may be organised into the following linear system:
 \begin{align} &\widetilde{\boldsymbol{M}} = \begin{bmatrix} -({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}){t_{{\underline{\beta }}}} (d_1{t_{{\overline{\gamma }}}}+1) & -{t_{{\underline{\alpha }}}} ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}) (d_1{t_{{\overline{\gamma }}}}+1) & - ({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}) ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}) (d_1{t_{{\overline{\gamma }}}}+1) \\ -({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}})(d_2{t_{{\underline{\beta }}}}-1){t_{{\overline{\gamma }}}} & -({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}) (d_2{t_{{\underline{\alpha }}}}{t_{{\overline{\gamma }}}}-1)& - ({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}) ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}) d_2{t_{{\overline{\gamma }}}} \\ -({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}) (d_3{t_{{\underline{\beta }}}}{t_{{\overline{\gamma }}}}-1) & - (d_3{t_{{\underline{\alpha }}}}+1) ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}){t_{{\overline{\gamma }}}} & -d_3 ({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}) ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}){t_{{\overline{\gamma }}}} \end{bmatrix}, \\[-3pt]\nonumber \end{align}
\begin{align} &\widetilde{\boldsymbol{M}} = \begin{bmatrix} -({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}){t_{{\underline{\beta }}}} (d_1{t_{{\overline{\gamma }}}}+1) & -{t_{{\underline{\alpha }}}} ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}) (d_1{t_{{\overline{\gamma }}}}+1) & - ({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}) ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}) (d_1{t_{{\overline{\gamma }}}}+1) \\ -({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}})(d_2{t_{{\underline{\beta }}}}-1){t_{{\overline{\gamma }}}} & -({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}) (d_2{t_{{\underline{\alpha }}}}{t_{{\overline{\gamma }}}}-1)& - ({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}) ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}) d_2{t_{{\overline{\gamma }}}} \\ -({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}) (d_3{t_{{\underline{\beta }}}}{t_{{\overline{\gamma }}}}-1) & - (d_3{t_{{\underline{\alpha }}}}+1) ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}){t_{{\overline{\gamma }}}} & -d_3 ({t_{{\overline{\alpha }}}}-{t_{{\underline{\alpha }}}}) ({t_{{\overline{\beta }}}}-{t_{{\underline{\beta }}}}){t_{{\overline{\gamma }}}} \end{bmatrix}, \\[-3pt]\nonumber \end{align}
The determinant of
![]() $\det (\widetilde{M})$
is given by
$\det (\widetilde{M})$
is given by
Eq. (38a) can yield a non-trivial solution iff
![]() $\det (\widetilde{M}) \ne 0$
, which is always the case. It is obvious that the first two factors in the R.H.S. of Eq. (39) cannot vanish. The third factor is always greater than unity, but it becomes infinite at a half-turn, which is excluded from this study (see Section 2). The last factor cannot vanish either, since it may be verified that the corresponding expression of
$\det (\widetilde{M}) \ne 0$
, which is always the case. It is obvious that the first two factors in the R.H.S. of Eq. (39) cannot vanish. The third factor is always greater than unity, but it becomes infinite at a half-turn, which is excluded from this study (see Section 2). The last factor cannot vanish either, since it may be verified that the corresponding expression of
![]() $d_1$
, when substituted back in Eqs. (37a–37c) makes the system inconsistent. Therefore, the solution for
$d_1$
, when substituted back in Eqs. (37a–37c) makes the system inconsistent. Therefore, the solution for
![]() $\tilde{\boldsymbol{x}}$
is obtained as
$\tilde{\boldsymbol{x}}$
is obtained as
Using Eqs. (40b–40d) in the identity
![]() $w ={\tilde{u}}{\tilde{v}}$
(see Eq. (38e)), one can eliminate
$w ={\tilde{u}}{\tilde{v}}$
(see Eq. (38e)), one can eliminate
![]() $\tilde{u}$
,
$\tilde{u}$
,
![]() $\tilde{v}$
simultaneously from Eqs. (37a–37c) to obtain the desired implicit form of
$\tilde{v}$
simultaneously from Eqs. (37a–37c) to obtain the desired implicit form of
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
in terms of
${\mathcal{Q}}_{{\overline{\gamma }}}$
in terms of
![]() $d_i$
:
$d_i$
:
The numerator of Eq. (41) defines an algebraic surface of degree two in
![]() $\{d_1,d_2,d_3\}$
:
$\{d_1,d_2,d_3\}$
:
In geometry, such a surface is known as a quadric. In the following, this quadric has been referred to as
![]() $\mathcal{U}_{{\overline{\gamma }}}$
and analysed further to ascertain its nature.
$\mathcal{U}_{{\overline{\gamma }}}$
and analysed further to ascertain its nature.
4.2. Characterisation of the quadric
 $\mathcal{U}_{{\overline{\gamma }}}$
$\mathcal{U}_{{\overline{\gamma }}}$
Eq. (42) may be cast in the following form:
 \begin{align} &{\boldsymbol{B} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & \frac{1}{\tan{\overline{\gamma }}}\\ 0 & \frac{1}{\tan{\overline{\gamma }}} & -1 \end{bmatrix}}, \\[-3pt]\nonumber \end{align}
\begin{align} &{\boldsymbol{B} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & \frac{1}{\tan{\overline{\gamma }}}\\ 0 & \frac{1}{\tan{\overline{\gamma }}} & -1 \end{bmatrix}}, \\[-3pt]\nonumber \end{align}
To comprehensively characterise the quadric one,
![]() $\mathcal{U}_{{\overline{\gamma }}}$
, needs to assess the ranks of
$\mathcal{U}_{{\overline{\gamma }}}$
, needs to assess the ranks of
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{B}$
, the sign of
$\boldsymbol{B}$
, the sign of
![]() $\det (\boldsymbol{E})$
and the signs of eigenvalues of
$\det (\boldsymbol{E})$
and the signs of eigenvalues of
![]() $\boldsymbol{B}$
(see, e.g., [Reference Zwillinger30], pp. 219–221). It may be readily verified that both
$\boldsymbol{B}$
(see, e.g., [Reference Zwillinger30], pp. 219–221). It may be readily verified that both
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{B}$
are of full rank, since
$\boldsymbol{B}$
are of full rank, since
The eigenvalues of
![]() $\boldsymbol{B}$
, denoted by
$\boldsymbol{B}$
, denoted by
![]() ${\lambda }_i, i=1,\dots, 3$
, are obtained as
${\lambda }_i, i=1,\dots, 3$
, are obtained as
Therefore,
![]() ${\lambda }_1,{\lambda }_3\gt 0,{\lambda }_2\lt 0 \ \forall{\overline{\gamma }} \in (0,\pi /2)$
. Based on these, it may be inferred that
${\lambda }_1,{\lambda }_3\gt 0,{\lambda }_2\lt 0 \ \forall{\overline{\gamma }} \in (0,\pi /2)$
. Based on these, it may be inferred that
![]() $\mathcal{U}_{{\overline{\gamma }}}$
is a hyperboloid of one sheet (see Figure 9). The sphere
$\mathcal{U}_{{\overline{\gamma }}}$
is a hyperboloid of one sheet (see Figure 9). The sphere
![]() $\mathcal{S}$
may now be identified as the largest one centred at the origin and tangent to
$\mathcal{S}$
may now be identified as the largest one centred at the origin and tangent to
![]() $\mathcal{U}_{{\overline{\gamma }}}$
. In order to simplify subsequent computations, the quadric
$\mathcal{U}_{{\overline{\gamma }}}$
. In order to simplify subsequent computations, the quadric
![]() $\mathcal{U}_{{\overline{\gamma }}}$
is first reduced to its canonical form, as described below.
$\mathcal{U}_{{\overline{\gamma }}}$
is first reduced to its canonical form, as described below.

Figure 9. Hyperboloid of sheet corresponding to the face
![]() $\mathcal{F}_{{\overline{\gamma }}}$
$\mathcal{F}_{{\overline{\gamma }}}$
![]() $(\gamma ={\overline{\gamma }}=50^\circ )$
and its local frame of reference (
$(\gamma ={\overline{\gamma }}=50^\circ )$
and its local frame of reference (
![]() $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
) represented in the global reference frame
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
) represented in the global reference frame
![]() $\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
.
$\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
.

Figure 10. Intersection of the plane
![]() $\mathcal{P}^{\prime}_2$
with the quadric
$\mathcal{P}^{\prime}_2$
with the quadric
![]() $\mathcal{U}_{{\overline{\gamma }}}$
and the sphere
$\mathcal{U}_{{\overline{\gamma }}}$
and the sphere
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
4.3. Reduction of
 $\mathcal{U}_{{\overline{\gamma }}}$
to its canonical form
$\mathcal{U}_{{\overline{\gamma }}}$
to its canonical form
The centre of a central quadric (denoted by
![]() $\boldsymbol{o}^{\prime}$
in the case of
$\boldsymbol{o}^{\prime}$
in the case of
![]() $\mathcal{U}_{{\overline{\gamma }}}$
) is characterised by the vanishing of the gradient vector to the quadratic expression of the surface at that point, that is:
$\mathcal{U}_{{\overline{\gamma }}}$
) is characterised by the vanishing of the gradient vector to the quadratic expression of the surface at that point, that is:
Upon solving Eq. (47), the desired centre,
![]() $\boldsymbol{o}^{\prime}$
, is obtained as
$\boldsymbol{o}^{\prime}$
, is obtained as
Eq. (48) places the centre
![]() $\boldsymbol{o}^{\prime}$
on the axis
$\boldsymbol{o}^{\prime}$
on the axis
![]() $\boldsymbol{d}_1$
of the global frame of reference,
$\boldsymbol{d}_1$
of the global frame of reference,
![]() $\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
, as shown in Figure 9. The canonical frame of reference of the hyperboloid (denoted by
$\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
, as shown in Figure 9. The canonical frame of reference of the hyperboloid (denoted by
![]() $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
) is determined by eigenvectors of
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
) is determined by eigenvectors of
![]() $\boldsymbol{B}$
, which are computed as
$\boldsymbol{B}$
, which are computed as
Given that the eigenvalues are distinct, the eigenvectors form an orthogonal basis, as shown in Figure 9. The axis
![]() $\boldsymbol{d}^{\prime}_1$
is aligned with the global coordinate axis
$\boldsymbol{d}^{\prime}_1$
is aligned with the global coordinate axis
![]() $\boldsymbol{d}_1$
, while
$\boldsymbol{d}_1$
, while
![]() $\boldsymbol{d}^{\prime}_2,\boldsymbol{d}^{\prime}_3$
span the plane
$\boldsymbol{d}^{\prime}_2,\boldsymbol{d}^{\prime}_3$
span the plane
![]() $d_1 = 0$
. The principal planes in
$d_1 = 0$
. The principal planes in
![]() $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
passing through
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
passing through
![]() $\boldsymbol{d}^{\prime}_1$
are denoted as
$\boldsymbol{d}^{\prime}_1$
are denoted as
![]() $\mathcal{P}^{\prime}_2$
(i.e.,
$\mathcal{P}^{\prime}_2$
(i.e.,
![]() $d^{\prime}_2=0)$
and
$d^{\prime}_2=0)$
and
![]() $\mathcal{P}^{\prime}_3$
(i.e.,
$\mathcal{P}^{\prime}_3$
(i.e.,
![]() $d^{\prime}_3=0)$
and are shown in Figures 10a and 11a, respectively. Finally,
$d^{\prime}_3=0)$
and are shown in Figures 10a and 11a, respectively. Finally,
![]() $\mathcal{U}_{{\overline{\gamma }}}$
may be expressed in its canonical form using the coordinates
$\mathcal{U}_{{\overline{\gamma }}}$
may be expressed in its canonical form using the coordinates
![]() $\boldsymbol{d}^{\prime}=[d^{\prime}_1,d^{\prime}_2,d^{\prime}_3]^{\top }$
through the following rigid transformation:
$\boldsymbol{d}^{\prime}=[d^{\prime}_1,d^{\prime}_2,d^{\prime}_3]^{\top }$
through the following rigid transformation:
 \begin{align} & \theta = \arccos \left (\frac{\boldsymbol{d}^{\prime}_2\cdot \boldsymbol{d}_2}{\sqrt{\boldsymbol{d}^{\prime}_2 \cdot \boldsymbol{d}^{\prime}_2}}\right ) ={\frac{1}{4}(3\pi - 2{\overline{\gamma }})}.\\[15pt]\nonumber \end{align}
\begin{align} & \theta = \arccos \left (\frac{\boldsymbol{d}^{\prime}_2\cdot \boldsymbol{d}_2}{\sqrt{\boldsymbol{d}^{\prime}_2 \cdot \boldsymbol{d}^{\prime}_2}}\right ) ={\frac{1}{4}(3\pi - 2{\overline{\gamma }})}.\\[15pt]\nonumber \end{align}
Using Eq. (50a) in Eq. (42) results in the standard form of the equation of the hyperboloid, denoted by
![]() $U^{\prime}_{{\overline{\gamma }}}$
:
$U^{\prime}_{{\overline{\gamma }}}$
:
Figures 10b and 11b depict the hyperboloid in its canonical frame (labelled as
![]() ${\mathcal{U}_{{\overline{\gamma }}}}^{\prime}$
).
${\mathcal{U}_{{\overline{\gamma }}}}^{\prime}$
).

Figure 11. Intersection of the plane
![]() $\mathcal{P}^{\prime}_3$
with the quadric
$\mathcal{P}^{\prime}_3$
with the quadric
![]() $\mathcal{U}_{{\overline{\gamma }}}$
and the sphere
$\mathcal{U}_{{\overline{\gamma }}}$
and the sphere
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
4.4. Identification of the largest contained sphere,
 $\mathcal{S}$
$\mathcal{S}$
The sphere
![]() $\mathcal{S}$
in
$\mathcal{S}$
in
![]() $\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
may also be transformed to the canonical frame
$\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
may also be transformed to the canonical frame
![]() $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
by substituting
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
by substituting
![]() $\boldsymbol{d}$
from Eq. (50a) in Eq. (18). This results in the following equation:
$\boldsymbol{d}$
from Eq. (50a) in Eq. (18). This results in the following equation:
In Eq. (54), the variable
![]() $r$
denotes the radius of the original sphere
$r$
denotes the radius of the original sphere
![]() $\mathcal{S}$
in
$\mathcal{S}$
in
![]() $\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
, as seen in Figure 14. The new sphere, labelled as
$\boldsymbol{o}\text{-}\boldsymbol{d}_1\boldsymbol{d}_2\boldsymbol{d}_3$
, as seen in Figure 14. The new sphere, labelled as
![]() ${\mathcal{S}}^{\prime}$
, in the frame
${\mathcal{S}}^{\prime}$
, in the frame
![]() $\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
is shown in Figures 10b and 11b. The centre of the sphere lies on the axis
$\boldsymbol{o}^{\prime}\text{-}\boldsymbol{d}^{\prime}_1\boldsymbol{d}^{\prime}_2\boldsymbol{d}^{\prime}_3$
is shown in Figures 10b and 11b. The centre of the sphere lies on the axis
![]() $\boldsymbol{d}^{\prime}_1$
as well. It is located at
$\boldsymbol{d}^{\prime}_1$
as well. It is located at
Because of this, the problem of determining the point of tangency between
![]() $\mathcal{S}$
and
$\mathcal{S}$
and
![]() $\mathcal{U}_{{\overline{\gamma }}}$
becomes a trivial one, since it now suffices to study the problem in either of the principal planes of the hyperboloid, given by
$\mathcal{U}_{{\overline{\gamma }}}$
becomes a trivial one, since it now suffices to study the problem in either of the principal planes of the hyperboloid, given by
![]() $\mathcal{P}^{\prime}_2$
or
$\mathcal{P}^{\prime}_2$
or
![]() $\mathcal{P}^{\prime}_3$
. The plane
$\mathcal{P}^{\prime}_3$
. The plane
![]() $\mathcal{P}^{\prime}_2$
is considered first.
$\mathcal{P}^{\prime}_2$
is considered first.
Setting
![]() $d^{\prime}_2$
to zero reduces Eq. (51) to that of an ellipse (denoted by
$d^{\prime}_2$
to zero reduces Eq. (51) to that of an ellipse (denoted by
![]() $\mathcal{X}_{\text{e}}$
), given by
$\mathcal{X}_{\text{e}}$
), given by
The centre of the ellipse is at the origin of the
![]() $\mathcal{P}^{\prime}_2$
plane, that is,
$\mathcal{P}^{\prime}_2$
plane, that is,
![]() $[0,0]^{\top }$
. The orientation of the ellipse can be determined by identifying its major axis. Given that
$[0,0]^{\top }$
. The orientation of the ellipse can be determined by identifying its major axis. Given that
 \begin{align*} \frac{a^{\prime}}{b^{\prime}} & = \frac{a^{\prime}}{\sqrt{a^{\prime}}} \quad \text{(see Eq. (53))}\\ & = \frac{1}{\sqrt{\sin{\overline{\gamma }}}}. \end{align*}
\begin{align*} \frac{a^{\prime}}{b^{\prime}} & = \frac{a^{\prime}}{\sqrt{a^{\prime}}} \quad \text{(see Eq. (53))}\\ & = \frac{1}{\sqrt{\sin{\overline{\gamma }}}}. \end{align*}
Hence,
![]() $a^{\prime}\gt b^{\prime} \ \forall{\overline{\gamma }} \in (0, \pi /2)$
. Thus, the major axis of the ellipse
$a^{\prime}\gt b^{\prime} \ \forall{\overline{\gamma }} \in (0, \pi /2)$
. Thus, the major axis of the ellipse
![]() $\mathcal{X}_{\text{e}}$
is along the axis
$\mathcal{X}_{\text{e}}$
is along the axis
![]() $\boldsymbol{d}^{\prime}_1$
.
$\boldsymbol{d}^{\prime}_1$
.
Similarly,
![]() ${\mathcal{S}}^{\prime}$
reduces to a circle (denoted by
${\mathcal{S}}^{\prime}$
reduces to a circle (denoted by
![]() $\mathcal{C}_{\text{e}}$
) in the plane
$\mathcal{C}_{\text{e}}$
) in the plane
![]() $\mathcal{P}^{\prime}_2$
, whose equation is given by
$\mathcal{P}^{\prime}_2$
, whose equation is given by
The centre of
![]() $\mathcal{C}_{\text{e}}$
also lies on the axis
$\mathcal{C}_{\text{e}}$
also lies on the axis
![]() $\boldsymbol{d}^{\prime}_1$
and is located at
$\boldsymbol{d}^{\prime}_1$
and is located at
![]() $\boldsymbol{o}^{\prime}_{\text{e}}=(1/\tan{\overline{\gamma }})[1,0]^{\top }$
(in the
$\boldsymbol{o}^{\prime}_{\text{e}}=(1/\tan{\overline{\gamma }})[1,0]^{\top }$
(in the
![]() $\mathcal{P}^{\prime}_2$
plane).
$\mathcal{P}^{\prime}_2$
plane).

Figure 12. Ellipse and circle resulting from intersection of
![]() $\mathcal{P}^{\prime}_2$
with
$\mathcal{P}^{\prime}_2$
with
![]() ${\mathcal{U}^{\prime}_{{\overline{\gamma }}}}$
and
${\mathcal{U}^{\prime}_{{\overline{\gamma }}}}$
and
![]() ${\mathcal{S}}^{\prime}$
, respectively.
${\mathcal{S}}^{\prime}$
, respectively.

Figure 13. Hyperbola and circle resulting from intersection of
![]() $\mathcal{P}^{\prime}_3$
with
$\mathcal{P}^{\prime}_3$
with
![]() ${\mathcal{U}^{\prime}_{{\overline{\gamma }}}}$
and
${\mathcal{U}^{\prime}_{{\overline{\gamma }}}}$
and
![]() ${\mathcal{S}}^{\prime}$
, respectively.
${\mathcal{S}}^{\prime}$
, respectively.
Furthermore, the centre of
![]() $\mathcal{C}_{\text{e}}$
lies inside
$\mathcal{C}_{\text{e}}$
lies inside
![]() $\mathcal{X}_{\text{e}}$
, since
$\mathcal{X}_{\text{e}}$
, since
![]() $\operatorname{sgn}(C_{\text{e}}) = \operatorname{sgn}(X_{\text{e}}) = -1$
, when evaluated at their respective centres. Therefore, the radii of the circles tangent to
$\operatorname{sgn}(C_{\text{e}}) = \operatorname{sgn}(X_{\text{e}}) = -1$
, when evaluated at their respective centres. Therefore, the radii of the circles tangent to
![]() $\mathcal{X}_{\text{e}}$
and centred at
$\mathcal{X}_{\text{e}}$
and centred at
![]() $\boldsymbol{o}^{\prime}_{\text{e}}$
are given by (see Figure 12):
$\boldsymbol{o}^{\prime}_{\text{e}}$
are given by (see Figure 12):
Obviously,
![]() $r^{\prime}_1 \le r^{\prime}_2\;\forall{\overline{\gamma }} \in (0,\pi /2)$
(as mentioned in Section 2). Hence, the largest circle centred at
$r^{\prime}_1 \le r^{\prime}_2\;\forall{\overline{\gamma }} \in (0,\pi /2)$
(as mentioned in Section 2). Hence, the largest circle centred at
![]() $\boldsymbol{o}^{\prime}_{\text{e}}$
and contained within
$\boldsymbol{o}^{\prime}_{\text{e}}$
and contained within
![]() $\mathcal{X}_{\text{e}}$
, and consequently, the desired largest sphere centred at
$\mathcal{X}_{\text{e}}$
, and consequently, the desired largest sphere centred at
![]() $\boldsymbol{d}$
contained inside
$\boldsymbol{d}$
contained inside
![]() $\mathcal{U}_{{\overline{\gamma }}}$
share the radius
$\mathcal{U}_{{\overline{\gamma }}}$
share the radius
![]() $r^{\prime}_1=r ={t_{{\overline{\gamma }}}}$
. Furthermore, the relevant point of tangency is found to be the terminal point of the major axis of the ellipse/hyperbola lying on the positive
$r^{\prime}_1=r ={t_{{\overline{\gamma }}}}$
. Furthermore, the relevant point of tangency is found to be the terminal point of the major axis of the ellipse/hyperbola lying on the positive
![]() $\boldsymbol{d}^{\prime}_1$
coordinate axis. Hence, in the 3D space of Rodrigues parameters
$\boldsymbol{d}^{\prime}_1$
coordinate axis. Hence, in the 3D space of Rodrigues parameters
![]() $\{d_1,d_2,d_3\}$
, the relevant point of tangency is given by
$\{d_1,d_2,d_3\}$
, the relevant point of tangency is given by
Identical results may be obtained by considering
![]() $\mathcal{P}^{\prime}_3$
plane, wherein the same problem is reduced to the tangency between a circle,
$\mathcal{P}^{\prime}_3$
plane, wherein the same problem is reduced to the tangency between a circle,
![]() $\mathcal{C}_{\text{h}}$
, and a hyperbola,
$\mathcal{C}_{\text{h}}$
, and a hyperbola,
![]() $\mathcal{X}_{\text{h}}$
, as shown in Figure 13. The computations involved are trivial in nature, and are, therefore, omitted for the sake of brevity.
$\mathcal{X}_{\text{h}}$
, as shown in Figure 13. The computations involved are trivial in nature, and are, therefore, omitted for the sake of brevity.

Figure 14. Sphere
![]() $\mathcal{S}$
that is tangent to
$\mathcal{S}$
that is tangent to
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
(and
${\mathcal{Q}}_{{\overline{\gamma }}}$
(and
![]() $\mathcal{U}_{{\overline{\gamma }}}$
) at
$\mathcal{U}_{{\overline{\gamma }}}$
) at
![]() $\overline{\boldsymbol{m}}^*$
.
$\overline{\boldsymbol{m}}^*$
.
Figures 12 and 13 depict
![]() $\mathcal{C}_{\text{e}}$
and
$\mathcal{C}_{\text{e}}$
and
![]() $\mathcal{C}_{\text{h}}$
of radius
$\mathcal{C}_{\text{h}}$
of radius
![]() $r^{\prime}_1$
that are tangent to
$r^{\prime}_1$
that are tangent to
![]() $\mathcal{X}_{\text{e}}$
and
$\mathcal{X}_{\text{e}}$
and
![]() $\mathcal{X}_{\text{h}}$
, respectively. Similarly, Figure 14 shows that
$\mathcal{X}_{\text{h}}$
, respectively. Similarly, Figure 14 shows that
![]() $\mathcal{S}$
is tangent to both
$\mathcal{S}$
is tangent to both
![]() ${\mathcal{Q}}_{{\overline{\gamma }}}$
and
${\mathcal{Q}}_{{\overline{\gamma }}}$
and
![]() $\mathcal{U}_{{\overline{\gamma }}}$
at
$\mathcal{U}_{{\overline{\gamma }}}$
at
![]() $\overline{\boldsymbol{m}}^*$
. Finally, to determine the parameters
$\overline{\boldsymbol{m}}^*$
. Finally, to determine the parameters
![]() $\{{\tilde{u}},{\tilde{v}}\}$
corresponding to the point of tangency, the coordinates of the point
$\{{\tilde{u}},{\tilde{v}}\}$
corresponding to the point of tangency, the coordinates of the point
![]() $\overline{\boldsymbol{m}}^*$
are inserted in Eqs. (40b) and (40c), resulting in the following expressions:
$\overline{\boldsymbol{m}}^*$
are inserted in Eqs. (40b) and (40c), resulting in the following expressions:
Given that the ranges of Euler angles used in this work are symmetric, the corresponding numerical values are
An assumption made earlier in this work, namely,
![]() $D \ne 0$
(see Section 4.1), may now be verified. Using Eqs. (61) and (3) in Eq. (37d), one finds
$D \ne 0$
(see Section 4.1), may now be verified. Using Eqs. (61) and (3) in Eq. (37d), one finds
5. Numerical Examples
The theoretical results derived above are numerically illustrated in this section. All the computations have been performed using a computer algebra system (CAS), namely, Mathematica 13.1 [31]. The ranges of Euler angles are chosen to be symmetric. However, both the cases of uniform and non-uniform ranges are studied. The corresponding numerical data are presented in Table III, while the locations of the corner points of corresponding
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
have been listed in Table IV.
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
have been listed in Table IV.
From Table IV, it is evident that for the non-uniform rangesFootnote
8
of Euler angles, the corresponding vertices of
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
maintain the central symmetry about the origin. The points
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
maintain the central symmetry about the origin. The points
![]() $\boldsymbol{m}_i$
and their counterparts
$\boldsymbol{m}_i$
and their counterparts
![]() $\boldsymbol{n}_j$
have been placed in the same rows in Table IV to accentuate this fact.
$\boldsymbol{n}_j$
have been placed in the same rows in Table IV to accentuate this fact.
5.1. Computation of the largest sphere
 $\overline{{\mathcal{S}}}$
contained in
$\overline{{\mathcal{S}}}$
contained in
 $\mathcal{V}_{\mathcal{R}}$
$\mathcal{V}_{\mathcal{R}}$
Both uniform and non-uniform ranges are used for demonstrating the computation of the largest contained spheres. The formulation and analytical computations were elaborated above in the context of the Z-Y-X and X-Y-Z sequences of Euler angles. However, the method has been applied to all the other asymmetric/Tait–Bryan sequences, that is, X-Z-Y, Y-X-Z, Y-Z-X, and Z-X-Y, for the sake of completeness. The corresponding results are summarised in Table VII. In all the cases, the analytical results are verified against results obtained from independently performed numerical optimisation, employing the in-built module NMinimize Footnote 9 of Mathematica 13.1. In all the cases, the corresponding results are found to agree up to 5 digits after the decimal.
For the “proper” Euler angle sequences, e.g.,
![]() $Z$
-
$Z$
-
![]() $Y$
-
$Y$
-
![]() $Z$
,
$Z$
,
![]() $Z$
-
$Z$
-
![]() $X$
-
$X$
-
![]() $Z$
and so on, the bounding hyperboloids pass through the origin, as shown in Figures 15a and 15b. Therefore, the volume contained between these around the origin vanishes identically, as shown in Figure 16. While this fact has been depicted visually in the context of the surfaces corresponding to
$Z$
and so on, the bounding hyperboloids pass through the origin, as shown in Figures 15a and 15b. Therefore, the volume contained between these around the origin vanishes identically, as shown in Figure 16. While this fact has been depicted visually in the context of the surfaces corresponding to
![]() $\mathcal{F}_{{\overline{\gamma }}}$
and
$\mathcal{F}_{{\overline{\gamma }}}$
and
![]() $\mathcal{F}_{{\overline{\alpha }}}$
in the said figures, respectively (using the
$\mathcal{F}_{{\overline{\alpha }}}$
in the said figures, respectively (using the
![]() $Z$
-
$Z$
-
![]() $Y$
-
$Y$
-
![]() $Z$
Euler angle sequence), it holds in all the other such cases as well. As can be seen in Figure 16, multiple bounding surfaces of
$Z$
Euler angle sequence), it holds in all the other such cases as well. As can be seen in Figure 16, multiple bounding surfaces of
![]() $\mathcal{V}_{\mathcal{R}}$
intersect at the origin for such sequences, which, in turn, reduces the radius of the largest sphere centred at the origin of
$\mathcal{V}_{\mathcal{R}}$
intersect at the origin for such sequences, which, in turn, reduces the radius of the largest sphere centred at the origin of
![]() $\mathcal{V}_{\mathcal{R}}$
to zero. Therefore, such Euler angle sequences are not included in the above study.
$\mathcal{V}_{\mathcal{R}}$
to zero. Therefore, such Euler angle sequences are not included in the above study.

Figure 15. Surfaces corresponding to the non-uniform ranges of Euler angles
![]() $\{\alpha, \beta, \gamma \}\in\times$
$\{\alpha, \beta, \gamma \}\in\times$
![]() $ [-30^\circ, 30^\circ ] [-40^\circ, 40^\circ ]\times [-50^\circ, 50^\circ ]$
.
$ [-30^\circ, 30^\circ ] [-40^\circ, 40^\circ ]\times [-50^\circ, 50^\circ ]$
.

Figure 16. Intersection of the surfaces of
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}Z)$
for one instance of proper Euler angles.
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}Z)$
for one instance of proper Euler angles.
5.1.1. Computation of the sphere
 $\overline{{\mathcal{S}}}$
corresponding to the Z-Y-X and X-Y-Z sequences of rotations for non-uniform ranges of Euler angles
$\overline{{\mathcal{S}}}$
corresponding to the Z-Y-X and X-Y-Z sequences of rotations for non-uniform ranges of Euler angles
The computation of
![]() ${\mathcal{S}} \subset{\mathcal{V}_{\mathcal{R}}(Z\text{-}X\text{-}Y)}$
is considered first. The face
${\mathcal{S}} \subset{\mathcal{V}_{\mathcal{R}}(Z\text{-}X\text{-}Y)}$
is considered first. The face
![]() $\mathcal{F}_{{\overline{\gamma }}}$
is used for the sake of illustration. As explained before,
$\mathcal{F}_{{\overline{\gamma }}}$
is used for the sake of illustration. As explained before,
![]() $\{u,v\}=\{1/2,1/2\}$
is the only real critical point obtained for the face
$\{u,v\}=\{1/2,1/2\}$
is the only real critical point obtained for the face
![]() $\gamma ={\overline{\gamma }} = 50^\circ$
, as shown in Figure 7a. Corresponding to the values of
$\gamma ={\overline{\gamma }} = 50^\circ$
, as shown in Figure 7a. Corresponding to the values of
![]() $\{u,v\}$
, the critical value of the radius
$\{u,v\}$
, the critical value of the radius
![]() $r$
is computed from Eq. (30b) as
$r$
is computed from Eq. (30b) as
![]() $r = \tan (25^\circ ) \approx 0.4663$
.
$r = \tan (25^\circ ) \approx 0.4663$
.
The results corresponding to the remaining five faces may be found in a similar manner. In all the cases, the critical point in the parameter space corresponds to
![]() $\{1/2, 1/2\}$
, and the critical value of the radius matches the tangent of half of the limiting value of the Euler angle defining the face (see Table V). The details are skipped to avoid the repetition of identical analytical steps. As mentioned in Eq. (32), the radius of the largest fully contained sphere,
$\{1/2, 1/2\}$
, and the critical value of the radius matches the tangent of half of the limiting value of the Euler angle defining the face (see Table V). The details are skipped to avoid the repetition of identical analytical steps. As mentioned in Eq. (32), the radius of the largest fully contained sphere,
![]() $\overline{{\mathcal{S}}}$
, is obtained as
$\overline{{\mathcal{S}}}$
, is obtained as
![]() ${\overline{r}} = \tan (15^\circ ) \approx 0.2679$
and corresponding points of tangency are
${\overline{r}} = \tan (15^\circ ) \approx 0.2679$
and corresponding points of tangency are
![]() $\overline{\boldsymbol{m}}^*=[0,0,0.2679]^{\top }$
and
$\overline{\boldsymbol{m}}^*=[0,0,0.2679]^{\top }$
and
![]() $\underline{\boldsymbol{m}}^*=[0,0,-0.2679]^{\top }$
. This corresponds to the smallest limit among the three Euler angles, namely,
$\underline{\boldsymbol{m}}^*=[0,0,-0.2679]^{\top }$
. This corresponds to the smallest limit among the three Euler angles, namely,
![]() ${\overline{\alpha }} = 30^\circ$
, as shown in Figure 8a. The same process is repeated to find
${\overline{\alpha }} = 30^\circ$
, as shown in Figure 8a. The same process is repeated to find
![]() ${\overline{{\mathcal{S}}}} \subset{\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)}$
. Not surprisingly, the results are identical to the case of
${\overline{{\mathcal{S}}}} \subset{\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)}$
. Not surprisingly, the results are identical to the case of
![]() ${\overline{{\mathcal{S}}}} \subset{\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)}$
as depicted in Figure 8b.
${\overline{{\mathcal{S}}}} \subset{\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)}$
as depicted in Figure 8b.
Table V. Critical values of
![]() $\{u,v\}$
, and the corresponding points of tangency and radii of the largest included spheres in
$\{u,v\}$
, and the corresponding points of tangency and radii of the largest included spheres in
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
for non-uniform ranges of Euler angles.
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
for non-uniform ranges of Euler angles.

Table VI. Values of
![]() $\{u,v\}$
, corresponding
$\{u,v\}$
, corresponding
![]() $\underline{\boldsymbol{m}}^*$
,
$\underline{\boldsymbol{m}}^*$
,
![]() $\overline{\boldsymbol{m}}^*$
,
$\overline{\boldsymbol{m}}^*$
,
![]() $\underline{\boldsymbol{n}}^*$
,
$\underline{\boldsymbol{n}}^*$
,
![]() $\overline{\boldsymbol{n}}^*$
and
$\overline{\boldsymbol{n}}^*$
and
![]() $r$
of
$r$
of
![]() $\mathcal{S}$
in
$\mathcal{S}$
in
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
for uniform ranges of Euler angles.
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
for uniform ranges of Euler angles.

5.1.2. Computation of the sphere
 $\overline{{\mathcal{S}}}$
corresponding to the Z-Y-X and X-Y-Z rotation sequences using uniform ranges of Euler angles
$\overline{{\mathcal{S}}}$
corresponding to the Z-Y-X and X-Y-Z rotation sequences using uniform ranges of Euler angles
The uniform Euler angles listed in Table III are used for the computation of
![]() $\overline{{\mathcal{S}}}$
. Similar to the case of non-uniform Euler angles, the solution of the optimisation problem is
$\overline{{\mathcal{S}}}$
. Similar to the case of non-uniform Euler angles, the solution of the optimisation problem is
![]() $\{u,v\}=\{1/2,1/2\}$
for each surface of
$\{u,v\}=\{1/2,1/2\}$
for each surface of
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
. The radii of the spheres tangent to the bounding surfaces, as well as the corresponding points of tangency, are listed in Table VI. As can be seen from the table, due to the symmetry in the limits of Euler angles, the radii of the said spheres are identical. Hence, the radius
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
. The radii of the spheres tangent to the bounding surfaces, as well as the corresponding points of tangency, are listed in Table VI. As can be seen from the table, due to the symmetry in the limits of Euler angles, the radii of the said spheres are identical. Hence, the radius
![]() $\overline{r}$
of the largest sphere
$\overline{r}$
of the largest sphere
![]() $\overline{{\mathcal{S}}}$
that fits inside
$\overline{{\mathcal{S}}}$
that fits inside
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
is evaluated as
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
is evaluated as
![]() ${\overline{r}}=\tan (15^\circ ) \approx 0.2679$
, as shown in Figure 17a. As
${\overline{r}}=\tan (15^\circ ) \approx 0.2679$
, as shown in Figure 17a. As
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
are related through the aforementioned central symmetry, and due to the uniformity in the ranges of Euler angles, the sphere
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
are related through the aforementioned central symmetry, and due to the uniformity in the ranges of Euler angles, the sphere
![]() $\overline{{\mathcal{S}}}$
corresponding to
$\overline{{\mathcal{S}}}$
corresponding to
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
is identical to the one corresponding to the Z-Y-X rotations, as shown in Figure 17b.
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
is identical to the one corresponding to the Z-Y-X rotations, as shown in Figure 17b.
Table VII. Results corresponding to Tait–Bryan sequence of rotations for non-uniform ranges of Euler angles listed in Table III.


Figure 17. Sphere
![]() $\overline{{\mathcal{S}}}$
inside
$\overline{{\mathcal{S}}}$
inside
![]() $\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
$\mathcal{V}_{\mathcal{R}}(Z\text{-}Y\text{-}X)$
and
![]() $\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
corresponding to the uniform ranges of Euler angles
$\mathcal{V}_{\mathcal{R}}(X\text{-}Y\text{-}Z)$
corresponding to the uniform ranges of Euler angles
![]() $\alpha, \beta, \gamma \in [-30^\circ, 30^\circ ]$
(refer to Table III). In each case,
$\alpha, \beta, \gamma \in [-30^\circ, 30^\circ ]$
(refer to Table III). In each case,
![]() $\overline{{\mathcal{S}}}$
is tangent to all the surfaces of the solid.
$\overline{{\mathcal{S}}}$
is tangent to all the surfaces of the solid.
5.1.3. Computation of the spheres corresponding to the X-Z-Y, Y-Z-X, Y-X-Z and Z-X-Y sequences for non-uniform ranges of Euler angles
The same procedure, as mentioned in Section 5.1.1, is followed to compute the largest sphere
![]() $\overline{{\mathcal{S}}}$
that fits inside
$\overline{{\mathcal{S}}}$
that fits inside
![]() ${\mathcal{V}_{\mathcal{R}}}(\text{{X}-{Z}-{Y}})$
,
${\mathcal{V}_{\mathcal{R}}}(\text{{X}-{Z}-{Y}})$
,
![]() ${\mathcal{V}_{\mathcal{R}}}(\text{{Y}-{Z}-{X})}$
,
${\mathcal{V}_{\mathcal{R}}}(\text{{Y}-{Z}-{X})}$
,
![]() ${\mathcal{V}_{\mathcal{R}}}(\text{{Y}-{X}-{Z}})$
, and
${\mathcal{V}_{\mathcal{R}}}(\text{{Y}-{X}-{Z}})$
, and
![]() ${\mathcal{V}_{\mathcal{R}}}(\text{{Z}-{X}-{Y}})$
, respectively, to cover comprehensively the remaining cases of Tait–Bryan sequences. The ranges of Euler angles are specified numerically in Table III. The included largest spheres are shown in Figures 18a, 18b, 18c and 18d, respectively.
${\mathcal{V}_{\mathcal{R}}}(\text{{Z}-{X}-{Y}})$
, respectively, to cover comprehensively the remaining cases of Tait–Bryan sequences. The ranges of Euler angles are specified numerically in Table III. The included largest spheres are shown in Figures 18a, 18b, 18c and 18d, respectively.
Table VII summarises the results for all of the six possible cases of Tait–Bryan angles. The results are identical since the radius of the largest included sphere,
![]() $\overline{r}$
, is given by the tangent of the half-angle corresponding to the smallest of the limiting values, that is,
$\overline{r}$
, is given by the tangent of the half-angle corresponding to the smallest of the limiting values, that is,
![]() $\overline{\phi } = \min \{{\overline{\alpha }},{\overline{\beta }},{\overline{\gamma }}\} ={\overline{\alpha }}$
, in this case (see Table III).
$\overline{\phi } = \min \{{\overline{\alpha }},{\overline{\beta }},{\overline{\gamma }}\} ={\overline{\alpha }}$
, in this case (see Table III).

Figure 18. Solids corresponding to the non-uniform ranges of Euler angles
![]() $\{\alpha, \beta, \gamma \}\in$
$\{\alpha, \beta, \gamma \}\in$
![]() $[-30^\circ, 30^\circ ]\times [-40^\circ, 40^\circ ]\times [-50^\circ, 50^\circ ]$
(refer to Table III). In each case,
$[-30^\circ, 30^\circ ]\times [-40^\circ, 40^\circ ]\times [-50^\circ, 50^\circ ]$
(refer to Table III). In each case,
![]() $\overline{{\mathcal{S}}}$
is tangent to the surface of the solids corresponding to the face
$\overline{{\mathcal{S}}}$
is tangent to the surface of the solids corresponding to the face
![]() $\alpha =30^\circ$
.
$\alpha =30^\circ$
.
6. Summary and discussions
The main results and the contributions of this article are discussed briefly in this section.
This article studies different representations of
![]() $\mathbb{SO}(3)$
, in order to explore the possibility of using them to describe subsets of
$\mathbb{SO}(3)$
, in order to explore the possibility of using them to describe subsets of
![]() $\mathbb{SO}(3)$
geometrically, in a manner that is both simple and physically meaningful. This is a non-trivial problem since not all mathematical structures are compatible with all the parametrisations of
$\mathbb{SO}(3)$
geometrically, in a manner that is both simple and physically meaningful. This is a non-trivial problem since not all mathematical structures are compatible with all the parametrisations of
![]() $\mathbb{SO}(3)$
; for example, it is meaningless to employ the Euclidean metric to compute the “distance between two rotations” in the Euler angle parametrisation. Therefore, proper combinations of parametrisations and choice of geometric shapes to describe the subsets are important. This is achieved in this article by using the Rodrigues parameters for computations, owing to the existence of a valid measure of distance from the origin in its own neighbourhood.
$\mathbb{SO}(3)$
; for example, it is meaningless to employ the Euclidean metric to compute the “distance between two rotations” in the Euler angle parametrisation. Therefore, proper combinations of parametrisations and choice of geometric shapes to describe the subsets are important. This is achieved in this article by using the Rodrigues parameters for computations, owing to the existence of a valid measure of distance from the origin in its own neighbourhood.
The theme of this article is entirely novel. It looks into descriptions of subsets in
![]() $\mathbb{SO}(3)$
and their relations, which, surprisingly, find no mention in the existing literature. For example, cuboids in the space of Euler angles are used quite commonly for this purpose, even though the validity or physical implications of the same have not been documented ever, to the best of the knowledge of the authors. This leaves some pertinent questions unanswered; for instance, given two cuboids, how does one find the set of rotations which are included in both? Or, how does one decide which one is “bigger” based on a physically meaningful and mathematically admissible scalar quantifier?
$\mathbb{SO}(3)$
and their relations, which, surprisingly, find no mention in the existing literature. For example, cuboids in the space of Euler angles are used quite commonly for this purpose, even though the validity or physical implications of the same have not been documented ever, to the best of the knowledge of the authors. This leaves some pertinent questions unanswered; for instance, given two cuboids, how does one find the set of rotations which are included in both? Or, how does one decide which one is “bigger” based on a physically meaningful and mathematically admissible scalar quantifier?
In order to investigate these cuboids further, they are first mapped to the space of Rodrigues parameters. This causes significant changes in their geometry, as each face of the cuboids transforms into a patch on the corresponding hyperboloid of one sheet. Accordingly, the cuboids map into solids which look as though they have been twisted about all the three coordinate axes (see Figure 6). Since these complicated shapes impede further analysis, such as a quantitative assessment of their extents, it is sought to identify the largest sphere, centred at the origin, that they enclose. This makes these solids comparable, in terms of the largest spheres (centred at the origin) that they fully enclose.
Furthermore, such a sphere has a great physical significance, as its radius equals
![]() $\tan (\overline{\phi }/2)$
, where
$\tan (\overline{\phi }/2)$
, where
![]() $\overline{\phi }$
is the maximum angle of rotation that one can achieve about all the spatial directions without violating the limits on the Euler angles specified originally. It is also shown, via direct computation, that irrespective of the Euler angle sequence considered (albeit with a restriction to the Tait–Bryan/Cardan types), the value of
$\overline{\phi }$
is the maximum angle of rotation that one can achieve about all the spatial directions without violating the limits on the Euler angles specified originally. It is also shown, via direct computation, that irrespective of the Euler angle sequence considered (albeit with a restriction to the Tait–Bryan/Cardan types), the value of
![]() $\overline{\phi }$
always equals the least absolute value of the limits on the individual Euler angles. Thus, the radius
$\overline{\phi }$
always equals the least absolute value of the limits on the individual Euler angles. Thus, the radius
![]() $\overline{r}$
affords a physically significant quantifiable measure for the extent of rotations permissible within the original cuboid of Euler angles. Moreover, given the simplicity and closed-form nature of the final expression of
$\overline{r}$
affords a physically significant quantifiable measure for the extent of rotations permissible within the original cuboid of Euler angles. Moreover, given the simplicity and closed-form nature of the final expression of
![]() $\overline{\phi }$
, no computation is required for practical applications of this measure in design and path planning. Moreover, in instances of design applications, Rodrigues parametrisation can be more appropriate than Euler angles. For example, [Reference Kingsley, Martin and Gasho32] describes a Stewart platform manipulator, which is to be used to mount an antenna that tracks the satellite, as it travels over an entire hemisphere. In this case, it is intuitive and trivial to express the desired range of orientations of the moving platform in terms of the normal to the platform, and eventually in terms of Rodrigues parameters, considering the normal to be the axis of non-zero net rotations. In contrast, it is not clear as to what might the required range of Euler angles be to cover the specified range of orientations.
$\overline{\phi }$
, no computation is required for practical applications of this measure in design and path planning. Moreover, in instances of design applications, Rodrigues parametrisation can be more appropriate than Euler angles. For example, [Reference Kingsley, Martin and Gasho32] describes a Stewart platform manipulator, which is to be used to mount an antenna that tracks the satellite, as it travels over an entire hemisphere. In this case, it is intuitive and trivial to express the desired range of orientations of the moving platform in terms of the normal to the platform, and eventually in terms of Rodrigues parameters, considering the normal to be the axis of non-zero net rotations. In contrast, it is not clear as to what might the required range of Euler angles be to cover the specified range of orientations.
This study legitimises the use of the cuboids in Euler angles (of the Tait–Bryan/Cardan types) to describe subsets of
![]() $\mathbb{SO}(3)$
. It can be stated with confidence that any specification of the orientation workspace of a manipulator in terms of permissible Euler angles as
$\mathbb{SO}(3)$
. It can be stated with confidence that any specification of the orientation workspace of a manipulator in terms of permissible Euler angles as
![]() $\alpha \in [{\underline{\alpha }},{\overline{\alpha }}]$
,
$\alpha \in [{\underline{\alpha }},{\overline{\alpha }}]$
,
![]() $\beta \in [{\underline{\beta }},{\overline{\beta }}]$
and
$\beta \in [{\underline{\beta }},{\overline{\beta }}]$
and
![]() $\gamma \in [{\underline{\gamma }},{\overline{\gamma }}]$
implies that all rotations about all possible axes in space are permissible to the extent of
$\gamma \in [{\underline{\gamma }},{\overline{\gamma }}]$
implies that all rotations about all possible axes in space are permissible to the extent of
![]() $\overline{\phi } = \operatorname{min}\{|{\underline{\alpha }}|,|{\overline{\alpha }}|, |{\underline{\beta }}|,|{\overline{\beta }}|,|{\underline{\gamma }}|,|{\overline{\gamma }}|\}$
. Such a result does not seem to exist in the present literature.
$\overline{\phi } = \operatorname{min}\{|{\underline{\alpha }}|,|{\overline{\alpha }}|, |{\underline{\beta }}|,|{\overline{\beta }}|,|{\underline{\gamma }}|,|{\overline{\gamma }}|\}$
. Such a result does not seem to exist in the present literature.
All the studies presented in this article have been performed in the analytical form via symbolic computations using a CAS, so as to preserve the generality and exactness of the results. The numerical results have been added only for the sake of illustrations and verifications. It is expected that the novel insights and quantitative measures generated in this study regarding the specifications of orientation workspaces and their physical implications would be beneficial in the process of path planning and design of spatial manipulators, especially those of parallel architecture, as these typically have limited orientation workspaces as opposed to their serial counterparts.
7. Conclusions
This article addresses an important gap in the existing literature in relation to the description of orientation workspaces as subsets of
![]() $\mathbb{SO}(3)$
. Even though it is common to find specifications of such subsets in terms of cuboids in the space of Euler angles, their physical implications are not available in the literature. Neither can one find a scalar measure of the size of such subsets so that any two of these can be compared objectively. This article addresses these lacunæ by mapping the said cuboids to the space of Rodrigues parameters, to take advantage of the inherent measure of distance from the origin available in that space. Through exact analytical computations, the largest sphere which can be included inside such a mapped region is identified in the closed form. The radius of the said sphere provides the means for quantifying the size of the original cuboid. Thus, this study provides physical and mathematical insights into the subsets of
$\mathbb{SO}(3)$
. Even though it is common to find specifications of such subsets in terms of cuboids in the space of Euler angles, their physical implications are not available in the literature. Neither can one find a scalar measure of the size of such subsets so that any two of these can be compared objectively. This article addresses these lacunæ by mapping the said cuboids to the space of Rodrigues parameters, to take advantage of the inherent measure of distance from the origin available in that space. Through exact analytical computations, the largest sphere which can be included inside such a mapped region is identified in the closed form. The radius of the said sphere provides the means for quantifying the size of the original cuboid. Thus, this study provides physical and mathematical insights into the subsets of
![]() $\mathbb{SO}(3)$
, their geometry and sizes. It is hoped that these developments would help in the process of design and path planning of spatial robots, the ones with parallel architecture, in particular.
$\mathbb{SO}(3)$
, their geometry and sizes. It is hoped that these developments would help in the process of design and path planning of spatial robots, the ones with parallel architecture, in particular.
Acknowledgements
The authors would like to express their sincere gratitude to Professor Gökhan Kiper, Department of Mechanical Engineering, İzmir Institute of Technology, Turkey, for suggesting some key references included in this article.
Author contributions
This work was conceptualised and formulated mathematically by the last author. The first author implemented all the codes, generated all the results, tables and figures, created the draft of the paper and worked on its revisions. The last author also edited the paper, worked on the revisions and supervised the entire work.
Financial support
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Competing interests
The authors declare no conflicts of interest exist.
Ethical approval
Not applicable.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S0263574724001772.
Appendix
A. Geometry and algebraic structure of
 $\mathbb{SO}(3)$
$\mathbb{SO}(3)$
The group of rotations in three dimensions, namely,
![]() $\mathbb{SO}(3)$
, can be visualised as a ball in space (see, e.g., [Reference Isaev and Rubakov33], p. 78). Following the notations used in [Reference Montaldi, Ratiu and Society34], p. 261, the said ball,
$\mathbb{SO}(3)$
, can be visualised as a ball in space (see, e.g., [Reference Isaev and Rubakov33], p. 78). Following the notations used in [Reference Montaldi, Ratiu and Society34], p. 261, the said ball,
![]() $\mathbb{B}^3_\pi$
, is open in
$\mathbb{B}^3_\pi$
, is open in
![]() ${\mathbb{R}}^3$
. Its radius equals
${\mathbb{R}}^3$
. Its radius equals
![]() $\pi$
, and its centre, the origin of
$\pi$
, and its centre, the origin of
![]() $\mathbb{SO}(3)$
, corresponds to zero (net) rotation. The closure of this ball has a boundary in the form of
$\mathbb{SO}(3)$
, corresponds to zero (net) rotation. The closure of this ball has a boundary in the form of
![]() $S^2_\pi$
, that is, the sphere of radius
$S^2_\pi$
, that is, the sphere of radius
![]() $\pi$
, concentric with the ball. It is interesting to note that the antipodal points on this sphere, that is, terminal points of any diameter, are identical, since the rotation by
$\pi$
, concentric with the ball. It is interesting to note that the antipodal points on this sphere, that is, terminal points of any diameter, are identical, since the rotation by
![]() $\pi$
and
$\pi$
and
![]() $-\pi$
about the same axis leads to identical final orientations. This property has been presented pictorially in Fig. 19, via the example of an arbitrary diameter with endpoints
$-\pi$
about the same axis leads to identical final orientations. This property has been presented pictorially in Fig. 19, via the example of an arbitrary diameter with endpoints
![]() $\boldsymbol{e}$
and
$\boldsymbol{e}$
and
![]() $\boldsymbol{e}^{\prime}$
, wherein it is understood that
$\boldsymbol{e}^{\prime}$
, wherein it is understood that
![]() $\boldsymbol{e}^{\prime} \equiv \boldsymbol{e}$
. In light of these facts, it can be argued that
$\boldsymbol{e}^{\prime} \equiv \boldsymbol{e}$
. In light of these facts, it can be argued that
![]() $\mathbb{SO}(3)$
, or equivalently, the ball
$\mathbb{SO}(3)$
, or equivalently, the ball
![]() $\mathbb{B}^3_\pi$
together with the sphere
$\mathbb{B}^3_\pi$
together with the sphere
![]() $\mathbb{S}^2_\pi$
is homeomorphic to the projective space
$\mathbb{S}^2_\pi$
is homeomorphic to the projective space
![]() ${\mathbb{R}}\mathbb{P}^3$
(see, e.g., [Reference Selig35], p. 16). Also, it can be stated that the said ball double-covers
${\mathbb{R}}\mathbb{P}^3$
(see, e.g., [Reference Selig35], p. 16). Also, it can be stated that the said ball double-covers
![]() $\mathbb{SO}(3)$
.
$\mathbb{SO}(3)$
.

Figure 19. Representation of
![]() $\mathbb{SO}(3)$
as ball of radius
$\mathbb{SO}(3)$
as ball of radius
![]() $\pi$
in
$\pi$
in
![]() ${\mathbb{R}}^3$
. The antipodal points
${\mathbb{R}}^3$
. The antipodal points
![]() $\boldsymbol{e}$
and
$\boldsymbol{e}$
and
![]() $\boldsymbol{e}^{\prime}$
represent the same point in
$\boldsymbol{e}^{\prime}$
represent the same point in
![]() $\mathbb{SO}(3)$
.
$\mathbb{SO}(3)$
.
B. An analytical study of the denominators appearing in Eqs. (11a-11c) and Eqs. (12a-12c) with regard to the conditions for their vanishing
The common denominator appearing in the RHSs of Eqs. (11a–11c), that is,
![]() $A+B$
, may be cast in the following form:
$A+B$
, may be cast in the following form:
Letting
![]() $g$
to vanish, one can find the corresponding expressions of
$g$
to vanish, one can find the corresponding expressions of
![]() $\alpha$
as:
$\alpha$
as:
where
![]() $\operatorname{atan2}(K \sin x, K \cos x)$
denotes the four-quadrant inverse tangent function, that returns
$\operatorname{atan2}(K \sin x, K \cos x)$
denotes the four-quadrant inverse tangent function, that returns
![]() $x \in [0, 2\pi ]$
uniquely
$x \in [0, 2\pi ]$
uniquely
![]() $\forall K \in{\mathbb{R}}\setminus \{0\}$
. If Eq. (B5) has real solutions for any combination of
$\forall K \in{\mathbb{R}}\setminus \{0\}$
. If Eq. (B5) has real solutions for any combination of
![]() $\beta, \gamma \in [0, 2\pi ]$
, then
$\beta, \gamma \in [0, 2\pi ]$
, then
![]() $A+B = 0$
. To examine the possibility of this, the discriminant of Eq. (B1) is computed as:
$A+B = 0$
. To examine the possibility of this, the discriminant of Eq. (B1) is computed as:
Using Eqs. (B2–B4) in Eq. (B6), it can be seen that
![]() $\Delta$
vanishes identically, signifying that there exists a unique value of
$\Delta$
vanishes identically, signifying that there exists a unique value of
![]() $\alpha \in [0,2\pi ]$
for any real pair of
$\alpha \in [0,2\pi ]$
for any real pair of
![]() $\beta, \gamma$
, which forms a double root of Eq. (B1). The expression for the said value is given by:
$\beta, \gamma$
, which forms a double root of Eq. (B1). The expression for the said value is given by:
Figure 20 presents this solution graphically for
![]() $\beta, \gamma \in [{-}\pi, \pi ]$
.
$\beta, \gamma \in [{-}\pi, \pi ]$
.
The above analysis assumed
![]() $a^2 + b^2$
to be non-zero. When that is not the case, Eq. (B6) suggests that
$a^2 + b^2$
to be non-zero. When that is not the case, Eq. (B6) suggests that
![]() $c$
vanishes, too. Therefore, Eq. (B1) reduces to an identity; that is, it admits any
$c$
vanishes, too. Therefore, Eq. (B1) reduces to an identity; that is, it admits any
![]() $\alpha \in [0, 2\pi ]$
as a solution. However, the only combinations of
$\alpha \in [0, 2\pi ]$
as a solution. However, the only combinations of
![]() $\{\beta, \gamma \}$
where this can happen (in
$\{\beta, \gamma \}$
where this can happen (in
![]() $[0, 2\pi$
]) are
$[0, 2\pi$
]) are
![]() $\{0, \pi \}$
and
$\{0, \pi \}$
and
![]() $\{\pi, 0\}$
, which are not included in this analysis anyway.
$\{\pi, 0\}$
, which are not included in this analysis anyway.
The analysis of the denominator Eqs. (12a-12c), that is,
![]() $A-B$
, is performed in an identical manner. In this case, the coefficients appearing in Eqs. (B2-B4) change to:
$A-B$
, is performed in an identical manner. In this case, the coefficients appearing in Eqs. (B2-B4) change to:
However, the new discriminant
![]() $\Delta ^{\prime} = a^{\prime2} + b^{\prime2} - c^{\prime2} = \Delta = 0$
, identically. Hence, the results are analogous to those in the case of vanishing of
$\Delta ^{\prime} = a^{\prime2} + b^{\prime2} - c^{\prime2} = \Delta = 0$
, identically. Hence, the results are analogous to those in the case of vanishing of
![]() $A+B$
. The set of solutions has been presented visually in Figure 21. The same analysis extends to Eqs. (17a–17c) as well, leading to analogous results.
$A+B$
. The set of solutions has been presented visually in Figure 21. The same analysis extends to Eqs. (17a–17c) as well, leading to analogous results.
It may also be noted that the above analysis can be repeated considering either
![]() $\beta$
as a function of
$\beta$
as a function of
![]() $\alpha, \gamma$
or
$\alpha, \gamma$
or
![]() $\gamma$
as a function of
$\gamma$
as a function of
![]() $\alpha, \beta$
. However, that would not alter the nature of the results, since the expressions of
$\alpha, \beta$
. However, that would not alter the nature of the results, since the expressions of
![]() $A+B$
and
$A+B$
and
![]() $A-B$
are symmetric functions of the three angles,
$A-B$
are symmetric functions of the three angles,
![]() $\alpha, \beta, \gamma$
.
$\alpha, \beta, \gamma$
.