Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T18:08:57.394Z Has data issue: false hasContentIssue false
  • English
  • Français

People search via deep compressed sensing techniques

Published online by Cambridge University Press:  02 February 2022

Bing-Xian Lu ,
Yu-Chung Tsai  and
Kuo-Shih Tseng Open the ORCID record for Kuo-Shih Tseng [Opens in a new window]
Bing-Xian Lu
Affiliation:
Department of Mathematics, National Central University, Taiwan.
Yu-Chung Tsai
Affiliation:
Department of Mathematics, National Central University, Taiwan.
Kuo-Shih Tseng*
Affiliation:
Department of Mathematics, National Central University, Taiwan.
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

People search can be reformulated as submodular maximization problems to achieve solutions with theoretical guarantees. However, the number of submodular function outcome is 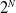$2^N$ from N sets. Compressing functions via nonlinear Fourier transform and spraying out sets are two ways to overcome this issue. This research proposed the submodular deep compressed sensing of convolutional sparse coding (SDCS-CSC) and applied the Topological Fourier Sparse Set (TFSS) algorithms to solve people search problems. The TFSS is based on topological and compressed sensing techniques, while the CSC is based on DCS techniques. Both algorithms enable an unmanned aerial vehicle to search for the people in environments. Experiments demonstrate that the algorithms can search for the people more efficiently than the benchmark approaches. This research also suggests how to select CSC or TFSS algorithms for different search problems.

Keywords

people searchsubmodularitydeep compressed sensingtopology
Type
Research Article
Information
Robotica , Volume 40 , Issue 7 , July 2022 , pp. 2320 - 2348
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Nemhauser, G. L., Wolsey, L. A. and Fisher, M. L., “An analysis of approximations for maximizing submodular set functions,” Math. Program. 14, 265–294 (1978).CrossRefGoogle Scholar
Feige, U., “A threshold of ln n for approximating set cover,” J. ACM 45(4), 634–652 (1998).CrossRefGoogle Scholar
Khuller, S., Moss, A. and Naor, J., “The budgeted maximum coverage problem,” Inform. Process. Lett. 70(1), 39–45 (1999).CrossRefGoogle Scholar
Zhang, H. and Vorobeychik, Y., “Submodular Optimization with Routing Constraints,” AAAI Conference on Artificial Intelligence,Arizona (2016).Google Scholar
Goemans, M., Harvey, N., Iwata, S. and Mirrokni, V., “Approximating Submodular Functions Everywhere,” ACM-SIAM Symposium on Discrete Algorithms,New York (2009).CrossRefGoogle Scholar
Stobbe, P. and Krause, A., “Learning Fourier Sparse Set Functions,” Proceedings of the Fifteenth International Conference on Artificial Intelligence and Statistics,Canary Islands (2012) pp. 1125–1133.Google Scholar
Tseng, K.-S., “Transfer learning of coverage functions via invariant properties in the fourier domain,” Autonom. Robots. 45(4), 519–542 (2021).CrossRefGoogle Scholar
Stone, L. D., “The theory of optimal search,” Oper. Res. Soc. Amer. (1975).Google Scholar
Trummel, K. E. and Weisinger, J. R., “The complexity of the optimal searcher path problem,” Oper. Res. 34(2), 324–327 (1986).CrossRefGoogle Scholar
Tseng, K.-S. and Mettler, B., “Near-optimal probabilistic search via submodularity and sparse regression,” Autonomo. Robots. 41(1), 205–229 (2015).CrossRefGoogle Scholar
Hollinger, G. and Sukhatme, G. S., “Sampling-Based Motion Planning for Robotic Information Gathering,” Robotics: Science and Systems Conference,Berlin (2013).CrossRefGoogle Scholar
H, G. ollinger, and Singh, S., “Proofs and Experiments in Scalable, Near-Optimal Search by Multiple Robots,” Robotics: Science and Systems, Zurich (2008) pp. 1426–1431.Google Scholar
Tsai, Y.-C., Lu, B.-X. and Tseng, K.-S., “Spatial Search via Adaptive Submodularity and Deep Learning,” IEEE International Symposium on Safety, Security, and Rescue Robotics,Würzburg (2019).CrossRefGoogle Scholar
Hollinger, G., Choudhuri, C., Mitra, U. and Sukhatme, G. S., “Squared Error Distortion Metrics for Motion Planning in Robotic Sensor Networks,” Proceedings International Workshop Wireless Networking for Unmanned Autonomous Vehicles, Atlanta (2013) pp. 1426–1431.Google Scholar
Balcan, M.-F. and Harvey, N. J. A., “Learning Submodular Functions,” Proceedings of the 43rd Annual ACM Symposium on Theory of Computing, San Jose (2011) pp. 793–802.Google Scholar
Tseng, K.-S. and Mettler, B., “Near-Optimal Probabilistic Search Using Spatial Fourier Sparse Set,” Autonomous Robots. 42, 329–351 (2017).Google Scholar
Sutskever, I., Krizhevsky, A. and Hinton, G. E., “Imagenet Classification with Deep Convolutional Neural Networks,” International Conference on Neural Information Processing Systems, Lake Tahoe, vol. 1 (2012) pp. 1097–1105.Google Scholar
Mnih, V., Kavukcuoglu, K., Silver, D., , A. A. Rusu, Veness, J., , M. G. Bellemare, Graves, A., Riedmiller, M., , A. K. Fidjeland, Ostrovski, G., Petersen, S., Beattie, C., Sadik, A., Antonoglou, I., King, H., Kumaran, D., Wierstra, D., Legg, S. and Hassabis, D., “Human-level control through deep reinforcement learning,” Nature 518, 529–533 (2015).CrossRefGoogle ScholarPubMed
Adler, A., Boublil, D. and Zibulevsky, M., “Block-Based Compressed Sensing of Images via Deep Learning,” IEEE International Workshop on Multimedia Signal Processing (MMSP),London-Luton (2017) pp. 1–6.Google Scholar
Shi, W., Jiang, F., Zhang, S. and Zhao, D., “Deep Networks for Compressed Image Sensing,” IEEE International Conference on Multimedia and Expo (ICME),Hong Kong (2017) pp. 877–882.Google Scholar
Kulkarni, K., Lohit, S., Turaga, P., Kerviche, R. and Ashok, A., “Reconnet: Non-Iterative Reconstruction of Images from Compressively Sensed Measurements,” IEEE Conference on Computer Vision and Pattern Recognition (CVPR),Las Vegas (2016) pp. 449–458.Google Scholar
Yao, H., Dai, F., Zhang, S., Zhang, Y., Tian, Q. and Xu, C., “Dr2-net: Deep residual reconstruction network for image compressive sensing,” Neurocomputing 359, 483–493 (2019).CrossRefGoogle Scholar
Canh, T. N. and Jeon, B., “Multi-scale deep compressive sensing network,” CoRR, abs/1809.05717 (2016).Google Scholar
Mousavi, A. and Baraniuk, R., “Learning to Invert: Signal Recovery via Deep Convolutional Networks,” IEEE International Conference on Acoustics, Speech and Signal Processing,New Orleans (2017) pp. 2272–2276.Google Scholar
Baraniuk, R. G., Mousavi, A. and , A. B. Patel, “A Deep Learning Approach to Structured Signal Recovery,” Annual Allerton Conference on Communication, Control, and Computing (Allerton),Urbana (2015) pp. 1336–1343.Google Scholar
Gregor, K. and LeCun, Y., “Learning Fast Approximations of Sparse Coding,” Proceedings of the 27th International Conference on Machine Learning,Haifa (2010) pp. 399–406.Google Scholar
Ito, D., Takabe, S., and Wadayama, T., “Trainable ista for sparse signal recovery,” IEEE Trans. Sig. Process. 67(12), 3113–3125 (2019).Google Scholar
Zhang, J. and Ghanem, B., “Ista-net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing,” IEEE Conference on Computer Vision and Pattern Recognition,Salt Lake City (2018) pp. 1828–1837.Google Scholar
Tsai, Y.-C. and Tseng, K.-S., “Deep compressed sensing for learning submodular functions,” Sensors 20(9), 2591(2020).CrossRefGoogle ScholarPubMed
Cohen-Steiner, D., Edelsbrunner, H. and Harer, J., “Stability of persistence diagrams,” Disc. Computat. Geom. 37(1), 103–120 (2007).CrossRefGoogle Scholar
Bhattacharya, S., Ghrist, R. and Kumar, V., “Persistent homology for path planning in uncertain environments,” IEEE Trans. Robot. 31(3), 578–590 (2015).Google Scholar
Govindarajan, V., Bhattacharya, S. and Kumar, V., “Human-robot collaborative topological exploration for search and rescue applications,” Distr. Autonom. Robot. Syst. 112, 17–32 (2016).CrossRefGoogle Scholar
de Silva, V. and Ghrist, R., “Coordinate-free coverage in sensor networks with controlled boundaries via homology,” Int. J. Robot. Res. 25(12), 1205–1222 (2006).CrossRefGoogle Scholar
Ramaithitima, R., Whitzer, M., Bhattacharya, S. and Kumar, V., “Sensor Coverage Robot Swarms using Local Sensing without Metric Information,” IEEE International Conference on Robotics and Automation,Seattle (2015) pp. 3408–3415.Google Scholar
Lu, B.-X., “3D map exploration and search using topological fourier sparse set,” Master thesis, National Central University (2020).Google Scholar
Baraniuk, R. G., “Compressive sensing,” IEEE Sig. Process. Mag. 24(4), 118–121 (2007).CrossRefGoogle Scholar
Tibshirani, R., “Regression shrinkage and selection via the lasso,” J. Roy. Stat. Soc. B 58(1), 267–288 (1996).Google Scholar
Tsai, Y.-C. and Tseng, K.-S., “Deep compressed sensing for learning submodular functions,” Sensors 20(9), 2591 (2020).CrossRefGoogle ScholarPubMed
Papyan, V., Sulam, J. and Elad, M., “Working locally thinking globally: Theoretical guarantees for convolutional sparse coding,” IEEE Trans. Sig. Process. 65(21), 5687–5701 (2017).Google Scholar
Papyan, V., Romano, Y. and Elad, M., “Convolutional neural networks analyzed via convolutional sparse coding,” J. Mach. Learn. Res. 18(1), 2887–2938 (2017).Google Scholar
Sulam, J., Papyant, V., Romano, Y. and Elad, M.. “Multilayer convolutional sparse modeling: Pursuit and dictionary learning,” IEEE Trans. Sig. Process. 66(15), 4090–4104 (2018).Google Scholar
Derenick, J., Kumar, V. and Jadbabaie, A., “Towards Simplicial Coverage Repair for Mobile Robot Teams,” IEEE International Conference on Robotics and Automation, Anchorage (2010).CrossRefGoogle Scholar
Rabadan, R. and Blumberg, A. J., Topological Data Analysis for Genomics and Evolution. (Cambridge University Press, New York, 2019).CrossRefGoogle Scholar
Chung, T. H. and Burdick, J. W., “Analysis of search decision making using probabilistic search strategies,” IEEE Trans. Robot. 28(1), 132–144 (2012).Google Scholar
Tseng, K.-S. and Mettler, B., “Human planning and coordination in spatial search problems,” 1st IFAC Conference on Cyber-Physical and Human-Systems, Florianopolis (2016).Google Scholar
Tseng, K.-S. and Mettler, B., “Analysis and augmentation of human performance on telerobotic search problems,” IEEE Access 8, 56590–56606 (2020).CrossRefGoogle Scholar
Tseng, K.-S. and Mettler, B., “Analysis of Coordination Patterns between Gaze and Control in Human Spatial Search,” 2nd IFAC Conference on Cyber-Physical and Human-Systems,Miami (2018) pp. 264–271.Google Scholar
Lu, B.-X., Wu, J.-J., Tsai, Y.-C., Jiang, W.-T. and Tseng, K.-S., “A Novel Telerobotic Search System Using An Unmanned Aerial Vehicle,” IEEE International Conference on Robotic Computing, Taichung (2020).CrossRefGoogle Scholar
Wulfmeier, M., Ondruska, P. and Posner, I., “Maximum entropy deep inverse reinforcement learning,” arxiv. (2015).Google Scholar