Article contents
Bayesian optimization for assist-as-needed controller in robot-assisted upper limb training based on energy information
Published online by Cambridge University Press: 10 July 2023
Abstract
The assist-as-needed (AAN) controller is effective in robot-assisted rehabilitation. However, variations of the engagement of subjects with fixed controller often lead to unsatisfying results. Therefore, adaptive AAN that adjusts control parameters based on individualized engagement is essential to enhance the training effect further. Nevertheless, current approaches mainly focus on the within-trial real-time engagement estimation, and the presence of measurement noise may cause improper evaluation of engagement. In addition, most studies on human-in-loop optimization strategies modulate the controller by greedy strategies, which are prone to fall into local optima. These shortcomings in previous studies could significantly limit the efficacy of AAN. This paper proposes an adaptive AAN to promote engagement by providing subjects with a subject-adaptive assistance level based on trial-wise engagement estimation and performance. Firstly, the engagement is estimated from energy information, which assesses the work done by the subject during a full trial to reduce the influence of measurement outliers. Secondly, the AAN controller is adapted by Bayesian optimization (BO) to maximize the subject’s performance according to historical trial-wise performance. The BO algorithm is good at dealing with noisy signals within limited steps. Experiments with ten healthy subjects resulted in a decrease of 34.59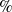 $\%$ in their average trajectory error, accompanied by a reduction of 9.71
$\%$ in their average trajectory error, accompanied by a reduction of 9.71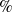 $\%$ in their energy consumption, thus verifying the superiority of the proposed method to prior work. These results suggest that the proposed method could potentially improve the effect of upper limb rehabilitation.
$\%$ in their energy consumption, thus verifying the superiority of the proposed method to prior work. These results suggest that the proposed method could potentially improve the effect of upper limb rehabilitation.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by


