Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T08:19:13.887Z Has data issue: false hasContentIssue false
  • English
  • Français

An efficient procedure for generating dynamic manipulator models*

Published online by Cambridge University Press:  09 March 2009

M. Vukobratović ,
Shi-Gang Li  and
N. Kirćanski
M. Vukobratović
Affiliation:
Institute Mihailo Pupin, P.O. Box 15, Beograd (Yugoslavia)
Shi-Gang Li
Affiliation:
Institute Mihailo Pupin, P.O. Box 15, Beograd (Yugoslavia)
N. Kirćanski
Affiliation:
Institute Mihailo Pupin, P.O. Box 15, Beograd (Yugoslavia)
Get access Rights & Permissions [Opens in a new window]

Summary

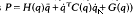An iterative procedure for obtaining dynamic model of manipulator has been proposed in this paper. The high efficiency of the procedure is reached on the basis of iterative relations of dynamic parameters. For general six revolute joint manipulator, the complete dynamic model i.e. matrices H(q), C(q), G(q) and vector of joint torques 13. requires 992 multiplications and 776 additions. When the complete dynamic model is given by 13. 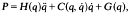the number of operations reduces to 863 multiplications and 773 additions.

Type
Article
Information
Robotica , Volume 3 , Issue 3 , September 1985 , pp. 147 - 152
Copyright
Copyright © Cambridge University Press 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Uicker, J.J., “On Dynamic Analysis of Spatial Linkages Using 4 × 4 Matrices” Ph.D. Dissertation (Northwestern University, Evanstone, August, 1965).Google Scholar
2.Kahn, M.E., “The Near Minimum Time Control of Open Loop Articulated Kinematic Chains Ph.D. Thesis (Stanford University, MEMO AIM. 106, 1969).Google Scholar
3.Woo, L.S. & Freudenstein, F., “Dynamic Analysis of Mechanisms Using Screw Coordinates” ASME Journal of Engineering for Industry 93, 273–276 (1971).CrossRefGoogle Scholar
4.Mahil, S.S., “On the Application of Lagrange's Method to the Description of Dynamic Systems” IEEE Trans on SMC 12, No. 6, 877–890 (1982).Google Scholar
5.Renaud, M., “Contribution a 1-Etude de la Modelisation et de la Commande des Systémes Mécaniques Articulés” Thése de Docteur-Ingénieur (Toulose, 1975).Google Scholar
6.Vukobratović, M. & Potkonjak, V., “Contribution to Automatic Forming of Active Chain Models via Lagrangian Form” ASME Journal of Applied Mechanics 46, No. 1, 181–185 (1979).CrossRefGoogle Scholar
7.Hollerbach, M., “A Recursive Lagrangian Formulation of Manipulator Dynamics and a Comparative Study of Dynamics Formulation Complexity” IEEE Trans on SMC 10, No. 11, 730–736 (1980).Google Scholar
8.Kane, T.R. & Wang, C.F., “On the Derivation of Equations of Motion” J. Soc. for md. and Appl. Math. 13, 487–492 (1965).Google Scholar
9.Huston, R.L., Posserello, C.E. & Harlow, M.W., “Dynamics of Multi-rigid-Body Systems” ASME Journal of Applied Mechanics 45, 889–894 (1978).CrossRefGoogle Scholar
10.Vukobratović, M. & Stepanenko, Y., “Mathematical Models of General Anthropomorphic Systems” Mathematical Biosciences 17, 191–242 (1973).CrossRefGoogle Scholar
11.Walker, M.W. & Orin, D.E., “Efficient Dynamic Computer Simulation of Robotic Mechanisms” Proc. of JACC (Charlotlesville, 1981).Google Scholar
12.Luh, J.Y.S., Walker, M.W. & Paul, R.P.C., “On-Line Computational Scheme for Mechanical Manipulators”, ASME Journal of Dynamic Systems, Measurement and Control 102, No. 2, 69–76 (1980).CrossRefGoogle Scholar
13.Luh, J.Y.S. & Lin, C.S., “Scheduling of Parallel Computation for Computer-Controlled Mechanical Manipulators” 12, No. 2, 214–234 (1982).Google Scholar
14.Aldon, M.J. & Liégeois, A., “Génération et Programmation Automatiques des Equations de Lagrange des Robots et Manipulators” Rapport de Recherche (INRIA, 1980).Google Scholar
15.Vukobratović, M. & Kiréanski, N., “Computer Assisted Generation of Robot Dynamic Models in Analytical Form” Acta Applicandae Mathematicae, International Journal of Applying Mathematics and Mathematical Applications 3, 49–70 (1985).CrossRefGoogle Scholar
16.Vukobratović, M. & Kirćanski, N., “A Method for Computer-Aided Construction of Analytical Models of Robotic Manipulators” First IEEE Conf. on Robotics (Atlanta, 1984).Google Scholar
17.Renaud, N., “An Efficient Iterative Analytical Procedure for Obtaining a Robot Manipulator Dynamic Model” Proc. of First International Symp. of Robotics Research (Bretton Woods, New Hampshire, MIT Press, 1983) pp. 749–762.Google Scholar
18.Fischer, O., Theoretische Grundlagen für eine Mechanik der lebenden Körper (TO Teubner, Berlin, 1906).Google Scholar
19.Wittenburg, J., Dynamics of Systems of Rigid Bodies (B.G. Teubner, 1977).CrossRefGoogle Scholar
20.Vukobratović, M. & Cvetković, V., “Computer-Oriented Algorithm of Variable Complexity for Mathematical Modeling of Active Mechanisms” IEEE Trans. on SMC SMC 12, No. 6, 838–848 (1982).Google Scholar
21.Paul, P.R., Robot Manipulators: Mathematics, Programming and Control (IMT Press, Cambridge, Massachusetts, 1981).Google Scholar