Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-31T20:27:12.501Z Has data issue: false hasContentIssue false
  • English
  • Français

VARIETIES OF POSITIVE MODAL ALGEBRAS AND STRUCTURAL COMPLETENESS

Published online by Cambridge University Press:  13 June 2019

TOMMASO MORASCHINI
TOMMASO MORASCHINI*
Affiliation:
Institute of Computer Science, Czech Academy of Science
*
*INSTITUTE OF COMPUTER SCIENCE CZECH ACADEMY OF SCIENCE PRAGUE, CZECH REPUBLIC E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Positive modal algebras are the 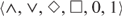$$\left\langle { \wedge , \vee ,\diamondsuit ,\square,0,1} \right\rangle $$-subreducts of modal algebras. We prove that the variety of positive S4-algebras is not locally finite. On the other hand, the free one-generated positive S4-algebra is shown to be finite. Moreover, we describe the bottom part of the lattice of varieties of positive S4-algebras. Building on this, we characterize (passively, hereditarily) structurally complete varieties of positive K4-algebras.

Keywords

03G2703B4554F05positive modal logicmodal logicstructural completenessadmissible ruleabstract algebraic logicalgebraization of Gentzen systems
Type
Research Article
Information
The Review of Symbolic Logic , Volume 12 , Issue 3 , September 2019 , pp. 557 - 588
Copyright
Copyright © Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Balan, A., Kurz, A., & Velebil, J. (2015). Positive fragments of coalgebraic logics. Logical Methods in Computer Science, 11(3), 1–51.CrossRefGoogle Scholar
Beklemishev, L. (2014). Positive provability logic for uniform reflection principles. Annals of Pure and Applied Logic, 165(1), 82–105.CrossRefGoogle Scholar
Beklemishev, L. (2018). A note on strictly positive logics and word rewriting systems. In Odintsov, S., editor. Larisa Maksimova on Implication, Interpolation, and Definability. Outstanding Contributions to Logic, Vol. 15. New York: Springer-Verlag, pp. 61–70.CrossRefGoogle Scholar
Bergman, C. (1991). Structural completeness in algebra and logic. In Andréka, H., Monk, J. D., and Nemeti, I., editors. Algebraic Logic (Budapest, 1988). Colloquia Mathematica Societatis János Bolyai, Vol. 54. Amsterdam: North-Holland, pp. 59–73.Google Scholar
Bergman, C. (2011). Universal Algebra: Fundamentals and Selected Topics. Chapman & Hall Pure and Applied Mathematics. Boca Raton, FL: Chapman and Hall/CRC.CrossRefGoogle Scholar
Bezhanishvili, G. & Grigolia, R. (2001). Locally tabular extensions of MIPC. In Zakharyaschev, M., Segerberg, K., de Rijke, M., and Wansing, H., editors. Advances in Modal Logic, Vol. 2. Stanford, CA: CSLI Publications, pp. 101–120.Google Scholar
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal Logic. Cambridge Tracts in Theoretical Computer Science, Vol. 53. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Blok, W. J. & Pigozzi, D. (1989). Algebraizable Logics. Memoirs of the American Mathematical Society, Vol. 396. Providence, RI: American Mathematical Society.Google Scholar
Burris, S. & Sankappanavar, H. P. (2012). A Course in Universal Algebra (millennium edition).Google Scholar
Celani, S. A. & Jansana, R. (1997). A new semantics for positive modal logic. Notre Dame Journal of Formal Logic, 38(1), 1–18.CrossRefGoogle Scholar
Celani, S. A. & Jansana, R. (1999). Priestley duality, a Sahlqvist theorem and a Goldblatt-Thomason theorem for positive modal logic. Logic Journal of the I.G.P.L., 7, 683–715.Google Scholar
Celani, S. A. (2006). Simple and subdirectly irreducibles bounded distributive lattices with unary operators. International Journal of Mathematics and Mathematical Sciences, 2006, 20.CrossRefGoogle Scholar
Chagrov, A. & Zakharyaschev, M. (1997). Modal Logic. Oxford Logic Guides, Vol. 35. Oxford: Oxford University Press.Google Scholar
Citkin, A. (1978). On structurally complete superintuitionistic logics. Soviet Mathematics Doklady, 19, 816–819.Google Scholar
Czelakowski, J. (2001). Protoalgebraic Logics. Trends in Logic—Studia Logica Library, Vol. 10. Dordrecht: Kluwer Academic Publishers.CrossRefGoogle Scholar
Czelakowski, J. & Dziobiak, W. (1990). Congruence distributive quasivarieties whose finitely subdirectly irreducible members form a universal class. Algebra Universalis, 27(1), 128–149.CrossRefGoogle Scholar
Davey, B. A. & Priestley, H. A. (2002). Introduction to Lattices and Order (second edition). New York: Cambridge University Press.CrossRefGoogle Scholar
Day, A. (1975). Splitting algebras and a weak notion of projectivity. Algebra Universalis, 5, 153–162.CrossRefGoogle Scholar
Dunn, J. M. (1995). Positive modal logic. Studia Logica, 55(2), 301–317CrossRefGoogle Scholar
Dzik, W. & Stronkowski, M. (2016). Almost structural completeness; an algebraic approach. Annals of Pure and Applied Logic, 167(7), 525–556.CrossRefGoogle Scholar
Dzik, W. & Wroński, A. (1973). Structural completeness of Gödel’s and Dummett’s propositional calculi. Studia Logica, 32, 69–73.CrossRefGoogle Scholar
Font, J. M. (2016). Abstract Algebraic Logic—An Introductory Textbook. Studies in Logic—Mathematical Logic and Foundations, Vol. 60. London: College Publications.Google Scholar
Font, J. M. & Jansana, R. (2009). A General Algebraic Semantics for Sentential Logics. A.S.L., second edition 2017 edition. Lecture Notes in Logic, Vol. 7. Cambridge: Cambridge University Press.Google Scholar
Freese, R., Kiss, E., & Valeriote, M. (2011). Universal Algebra Calculator. Available at: www.uacalc.org.Google Scholar
Gehrke, M., Nagahashi, H., & Venema, Y. (2005). A Sahlqvist theorem for distributive modal logic. Annals of Pure and Applied Logic, 131(1–3), 65–102.CrossRefGoogle Scholar
Gorbunov, V. A. (1976). Lattices of quasivarieties. Algebra and Logic, 15, 275–288.CrossRefGoogle Scholar
Gorbunov, V. A. (1998). Algebraic Theory of Quasivarieties. Siberian School of Algebra and Logic. New York: Consultants Bureau.Google Scholar
Hughes, G. E. & Cresswell, M. J. (1996). A New Introduction to Modal Logic. London: Routledge.CrossRefGoogle Scholar
Iemhoff, R. (2001). On the admissible rules of intuitionistic propositional logic. The Journal of Symbolic Logic, 66(1), 281–294.CrossRefGoogle Scholar
Jansana, R. (2002). Full models for positive modal logic. Mathematical Logic Quarterly, 48(3), 427–445.3.0.CO;2-T>CrossRefGoogle Scholar
Jeřábek, E. (2005). Admissible rules of modal logic. Journal of Logic and Computation, 15(4), 73–92.CrossRefGoogle Scholar
Johnstone, P. T. (1982). Stone Spaces. Cambridge Studies in Advanced Mathematics, Vol. 3. Cambridge: Cambridge University Press.Google Scholar
Johnstone, P. T. (1985). Vietoris locales and localic semilattices. In Hoffmann, R.-E. and Hofmann, K. H., editors. Continuous Lattices and their Applications. Lecture Notes in Pure and Applied Mathematics, Vol. 101. New York: Marcel Dekker, pp. 155–180.Google Scholar
Jónsson, B. (1970). Topics in Universal Algebra. Lecture Notes in Mathematics, Vol. 250. Berlin: Springer-Verlag.Google Scholar
Köhler, P. & Pigozzi, D. (1980). Varieties with equationally definable principal congruences. Algebra Universalis, 11, 213–219.CrossRefGoogle Scholar
Kracht, M. (1999). Tools and Techniques in Modal Logic. Studies in Logic and the Foundations of Mathematics, Vol. 142. Amsterdam: North-Holland.CrossRefGoogle Scholar
Kracht, M. (2006). Modal consequence relations. In Blackburn, P., van Benthem, J., and Wolter, F., editors. Handbook of Modal Logic, Vol. 3. New York: Elsevier, pp. 491–545.CrossRefGoogle Scholar
Maksimova, L. L. & Rybakov, V. V. (1974). A lattice of normal modal logics. Algebra and Logic, 13, 105–122.CrossRefGoogle Scholar
Mal’cev, A. I. (1971). The Metamathematics of Algebraic Systems, Collected Papers: 1936–1967. Amsterdam: North-Holland.Google Scholar
McKenzie, R. (1972). Equational bases and nonmodular lattice varieties. Transactions of the Americal Mathematical Society, 174, 1–43.CrossRefGoogle Scholar
McKenzie, R. N., McNulty, G. F., & Taylor, W. F. (1987). Algebras, Lattices, Varieties, Vol. I. The Wadsworth & Brooks/Cole Mathematics Series. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software.Google Scholar
McKinsey, J. C. C. & Tarski, A. (1944). The algebra of topology. Annals of Mathematics, 45, 141–191.CrossRefGoogle Scholar
Metcalfe, G. & Röthlisberger, C. (2013). Admissibility in finitely generated quasivarieties. Logical Methods in Computer Science, 9(2), 1–19.CrossRefGoogle Scholar
Moraschini, T., Raftery, J. G., & Wannenburg, J. J. (2019). Singly generated quasivarieties and residuated structures. Mathematical Logic Quarterly, to appear.Google Scholar
Nguyen, L. A. (2000). Constructing the least models for positive modal logic programs. Fundamenta Informaticae, 42(2), 29–60.Google Scholar
Nguyen, L. A. (2005). On the complexity of fragments of modal logics. In Schmidt, R., Pratt-Hartmann, I., Reynolds, M., and Wansing, H., editors. Advances in Modal Logic, Vol. 5. London: King’s College Publications, pp. 249–268.Google Scholar
Olson, J. S., Raftery, J. G., & van Alten, C. J. (2008). Structural completeness in substructural logics. Logic Journal of the I.G.P.L., 16(5), 455–495.Google Scholar
Palmigiano, A. (2003). Coalgebraic semantics for positive modal logic. In Gumm, H. P., editor. Electronic Notes in Theoretical Computer Science, Vol. 82. Amsterdam: Elsevier, pp. 221–236.Google Scholar
Priestley, H. A. (1970). Representation of distributive lattices by means of ordered Stone spaces. Bulletin of the London Mathematical Society, 2, 186–190.CrossRefGoogle Scholar
Priestley, H. A. (1972). Ordered topological spaces and the representation of distributive lattices. Proceedings of the London Mathematical Society. Third Series, 24, 507–530.CrossRefGoogle Scholar
Raftery, J. G. (2006). Correspondences between Gentzen and Hilbert systems. The Journal of Symbolic Logic, 71(3), 903–957.CrossRefGoogle Scholar
Raftery, J. G. (2016). Admissible rules and the Leibniz hierarchy. Notre Dame Journal of Formal Logic, 57(4), 569–606.CrossRefGoogle Scholar
Raftery, J. G. & Świrydowicz, K. (2016). Structural completeness in relevance logics. Studia Logica, 104(3), 381–387.CrossRefGoogle Scholar
Rautenberg, W. (1979). Klassische und nichklassische Aussagenlogik. Wiesbaden: Vieweg Verlag.CrossRefGoogle Scholar
Rebagliato, J. & Verdú, V. (1995). Algebraizable Gentzen Systems and the Deduction Theorem for Gentzen Systems. Mathematics Preprint Series, Vol. 175. Barcelona: University of Barcelona.Google Scholar
Rieger, L. (1957). Zamerka o t. naz. svobodnyh algebrah s zamykanijami. Czechoslovak Mathematical Journal, 7, 16–20.Google Scholar
Rybakov, V. V. (1995). Hereditarily structurally complete modals logics. The Journal of Symbolic Logic, 60(1), 266–288.CrossRefGoogle Scholar
Rybakov, V. V. (1997). Admissibility of Logical Inference Rules. Studies in Logic, Vol. 136. Amsterdam: Elsevier.CrossRefGoogle Scholar
Wroński, A. (2009). Overflow rules and a weakening of structural completeness. In Sytnik-Czetwertyński, J., editor. Rozwazania o Filozfii Prawdziwej. Jerezmu Perzanowskiemuw Darze. Kraków: Uniwersytetu Jagiellońskiego, pp. 67–71.Google Scholar