Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T07:18:01.988Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSITIVE PRIMAL INFON LOGIC

Published online by Cambridge University Press:  21 March 2013

CARLOS COTRINI  and
YURI GUREVICH
CARLOS COTRINI*
Affiliation:
Swiss Federal Institute of Technology
YURI GUREVICH*
Affiliation:
Microsoft Research
*
*CARLOS COTRINI, SWISS FEDERAL INSTITUTE OF TECHNOLOGY, ZÜ RICH, SWITZERLAND E-mail: [email protected]
†YURI GUREVICH, MICROSOFT RESEARCH, REDMOND, WA 98052 E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Primal infon logic was introduced in 2009 in connection with access control. In addition to traditional logic constructs, it contains unary connectives p said indispensable in the intended access control applications. Propositional primal infon logic is decidable in linear time, yet suffices for many common access control scenarios. The most obvious limitation on its expressivity is the failure of the transitivity law for implication: 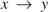$x \to y$ and 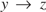$y \to z$ do not necessarily yield 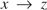$x \to z$. Here we introduce and investigate equiexpressive “transitive” extensions TPIL and TPIL* of propositional primal infon logic as well as their quote-free fragments TPIL0 and TPIL0* respectively. We prove the subformula property for TPIL0* and a similar property for TPIL*; we define Kripke models for the four logics and prove the corresponding soundness-and-completeness theorems; we show that, in all these logics, satisfiable formulas have small models; but our main result is a quadratic-time derivation algorithm for TPIL*.

Type
Research Article
Information
The Review of Symbolic Logic , Volume 6 , Issue 2 , June 2013 , pp. 281 - 304
Copyright
Copyright © Association for Symbolic Logic 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Avron, A., & Lahav, O. (2009). Canonical constructive systems. Proceedings of TABLEAUX 2009, 62–76.Google Scholar
Beklemishev, L., Blass, A., & Gurevich, Y.What is the logic of information? In preparation.Google Scholar
Beklemishev, L., & Gurevich, Y. (2012). Propositional primal logic with disjunction. Journal of Logic and Computation, published online May 29, 2012. doi:10.1093/logcom/exs018.Google Scholar
Bjørner, N., de Caso, G., & Gurevich, Y. (2012). From primal infon logic with individual variables to datalog. In Erdem, E., et al. ., editors. Correct Reasoning: Essays on Logic-Based AI in Honour of Vladimir Lifschitz, Springer Lecture Notes in Computer Science, Springer Verlag, Vol. 7265, pp. 72–86.CrossRefGoogle Scholar
Blass, A., & Gurevich, Y. (2010). Hilbertian deductive systems, infon logic, and datalog. Bulletin of the EATCS, 102, 122–150. A slightly revised version in Microsoft Research Tech, Report MSR-TR-2011-81, June 2011.Google Scholar
Blass, A., Gurevich, Y., Moskał, , & Neeman, I. (2011). Evidential authorization. In Nanz, S., editor. The Future of Software Engineering. Springer, 77–99.Google Scholar
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2001). Introduction to Algorithms (second edition). MIT Press and McGraw-Hill.Google Scholar
Cotrini, C., & Gurevich, Y. (2013). Basic primal infon logic. Journal of Logic and Computation.Google Scholar
Dantzin, E., Eiter, T., Gottlob, G., & Voronkov, A. (2001). Complexity and expressive power of logic programming. ACM Computing Surveys, 33(3), 374–425.CrossRefGoogle Scholar
DKAL at CodePlex. http://dkal.codeplex.com/, viewed August 10, 2012.Google Scholar
Dowling, W., & Gallier, J. (1984). Linear-time algorithms for testing the satisfiability of propositional Horn formulae. Journal of Logic Programming, 1, 267–284.CrossRefGoogle Scholar
Fortnow, L. (2009). Shaving logs with unit cost. http://blog.computationalcomplexity.org/2009/05/shaving-logs-with-unit-cost.html, seen July 22, 2012.Google Scholar
Gabbay, D., Kurucz, A., Wolter, F., & Zakharyaschev, M. (2003). Many-dimensional Modal Logics: Theory and Applications. Elsevier.Google Scholar
Gurevich, Y. (2011). Two Notes on Propositional Primal Logic. Technical Report MSR-TR-2011-70, Microsoft Research, May 2011.Google Scholar
Gurevich, Y., & Neeman, I. (2008). DKAL: Distributed-knowledge authorization language. In Proceedings of CSF 2008. IEEE Computer Society, pp. 149–162.Google Scholar
Gurevich, Y., & Neeman, I. (2009). DKAL 2 — A simplified and improved authorization language. Microsoft Research Tech Report MSR-TR-2009-11, February 2009.Google Scholar
Gurevich, Y., & Neeman, I. (2011). Infon logic: the propositional case. ACM Transactions on Computation Logic 12(2), Article 9, January 2011, and (slight revisied) Microsoft Research Tech. Report MSR-TR-2011-90, July 2011.Google Scholar
Halpern, J. (1995). The effect of bounding the number of primitive propositions and the depth of nesting on the complexity of modal logic. Artificial Intelligence, 75(2), 361–372.Google Scholar
Kurucz, A., Wolter, F., & Zakharyaschev, M. (2010). Islands of tractability for relational constraints: towards dichotomy results for the description logic EL, In Beklemishev, L., Goranko, V., and Shehtman, V., editors. Advances in Modal Logic, College Publications, Vol. 8, pp. 271–291.Google Scholar
Kurucz, A., Wolter, F., & Zakharyaschev, M. (2011). On P/NP dichotomies for EL subsumption under relational constraints. In Proceedings of DL 2011.Google Scholar
Minoux, M. (1988). LTUR: A simplified linear-time unit resolution algorithm for Horn formulae and computer implementation. Information Processing Letters, 29(1), 1–12.Google Scholar
Mints, G. (1992). Complexity of subclasses of the intuitionistic propositional calculus. BIT, 32, 64–69.Google Scholar
Savateev, Y. (2009). Investigation of Primal Logic. Unpublished internship (at Microsoft Research) report.Google Scholar
van Dalen, D. (2008). Logic and Structure (fourth edition). Springer.Google Scholar
Visser, A. (2012). Personal communication, January 7, 2012.Google Scholar
Visser, A., van Benthem, J., de Jongh, D., & de Lavalette, G. R. (2008). NNIL, a study in intuitionistic propositional logic. In Logic Group Preprint Series, Holland: Dept of Philosophy, Utrecht University, Vol. 111.Google Scholar
Wolter, F., & Zakharyaschev, M. (1999). Intuitionistic modal logic. In Cantini, A., Casari, E., and Minari, P., editors. Logic and Foundations of Mathematics. Kluwer Academic Publishers, pp. 227–238.Google Scholar