Article contents
SUBSTRUCTURAL INQUISITIVE LOGICS
Published online by Cambridge University Press: 01 February 2019
Abstract
This paper shows that any propositional logic that extends a basic substructural logic BSL (a weak, nondistributive, nonassociative, and noncommutative version of Full Lambek logic with a paraconsistent negation) can be enriched with questions in the style of inquisitive semantics and logic. We introduce a relational semantic framework for substructural logics that enables us to define the notion of an inquisitive extension of λ, denoted as 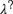 ${\lambda ^?}$, for any logic λ that is at least as strong as BSL. A general theory of these “inquisitive extensions” is worked out. In particular, it is shown how to axiomatize
${\lambda ^?}$, for any logic λ that is at least as strong as BSL. A general theory of these “inquisitive extensions” is worked out. In particular, it is shown how to axiomatize 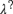 ${\lambda ^?}$, given the axiomatization of λ. Furthermore, the general theory is applied to some prominent logical systems in the class: classical logic Cl, intuitionistic logic Int, and t-norm based fuzzy logics, including for example Łukasiewicz fuzzy logic Ł. For the inquisitive extensions of these logics, axiomatization is provided and a suitable semantics found.
${\lambda ^?}$, given the axiomatization of λ. Furthermore, the general theory is applied to some prominent logical systems in the class: classical logic Cl, intuitionistic logic Int, and t-norm based fuzzy logics, including for example Łukasiewicz fuzzy logic Ł. For the inquisitive extensions of these logics, axiomatization is provided and a suitable semantics found.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2019
References
BIBLIOGRAPHY
- 16
- Cited by


