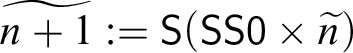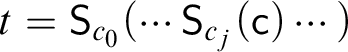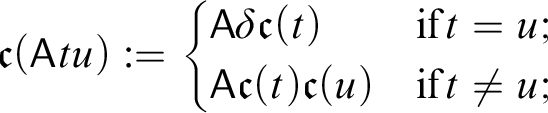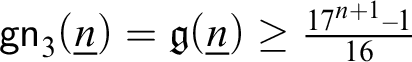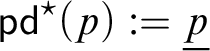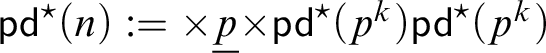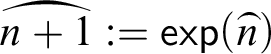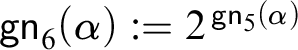1 Introduction
Notions of self-reference feature prominently in the philosophical literature, yet they are notoriously elusive and mostly left imprecise. The study of certain logical and philosophical issues, however, such as semantic paradoxes and the semantics of both natural and formal languages, requires a precise understanding of self-reference. For instance, an adequate evaluation of the contentious hypothesis that circularity lies at the root of all semantic paradoxes requires a satisfactory and precise explication of self-reference (see Reference Leitgeb[17]). Following the wide-spread custom of arithmetisation, the explication and investigation of self-reference is therefore typically carried out in a formal arithmetical framework.
There are essentially two ways an arithmetical sentence can be taken to (directly) refer to itself, namely, in virtue of containing a term denoting (the code of) itself, or by means of quantification Reference Leitgeb[17, Reference Picollo21].Footnote
1
In this paper we are only concerned with the first kind of self-reference, also called “self-reference by mention” or in short “m-self-reference” [Reference Picollo21, p. 581]. Halbach and Visser Reference Halbach and Visser[10] trace this notion of self-reference back to the famous exchange of Kreisel and Henkin regarding Henkin’s question as to whether sentences that state their own
![]() $\mathsf {PA}$
-provability are provable in
$\mathsf {PA}$
-provability are provable in
![]() $\mathsf {PA}$
. Heck Reference Heck[13], for instance, considers m-self-reference the only legitimate way to formalise truly self-referential reasoning in arithmetic. A precise notion of m-self-referentiality in an arithmetical framework rests on three formalisation choices:
$\mathsf {PA}$
. Heck Reference Heck[13], for instance, considers m-self-reference the only legitimate way to formalise truly self-referential reasoning in arithmetic. A precise notion of m-self-referentiality in an arithmetical framework rests on three formalisation choices:
-
i. a formal language
-
ii. a Gödel numbering
-
iii. a naming device
Given the central importance of m-self-reference in the literature, the primary concern of this paper is to examine the formalisation choices under which m-self-reference is attainable. That is, we ask for which choices of (i)–(iii) we can find for each formula
![]() $A(x)$
, with free variable x, a closed term t which denotes the Gödel code of
$A(x)$
, with free variable x, a closed term t which denotes the Gödel code of
![]() $A(t)$
.
$A(t)$
.
Let
![]() ${\mathcal {L}^0}$
be the arithmetical language which has
${\mathcal {L}^0}$
be the arithmetical language which has
![]() ${\sf 0}$
,
${\sf 0}$
,
![]() $\mathsf {S}$
,
$\mathsf {S}$
,
![]() $+$
and
$+$
and
![]() $\times $
as its non-logical vocabulary. Let
$\times $
as its non-logical vocabulary. Let
![]() $\xi $
be a standard numbering of
$\xi $
be a standard numbering of
![]() ${\mathcal {L}^0}$
and consider the canonical naming device which maps each number n to its standard numeral
${\mathcal {L}^0}$
and consider the canonical naming device which maps each number n to its standard numeral
![]() $\underline {n}$
. Taken together, these canonical formalisation choices do not, generally, permit the construction of m-self-referential sentences.Footnote
2
There are two well-known routes to overcome this.
$\underline {n}$
. Taken together, these canonical formalisation choices do not, generally, permit the construction of m-self-referential sentences.Footnote
2
There are two well-known routes to overcome this.
The first route consists in enriching the arithmetical language by function symbols for primitive recursive functions, such that the resulting language
![]() ${\mathcal {L}}^+$
contains a term
${\mathcal {L}}^+$
contains a term
![]() $\delta (x)$
which represents a diagonal function D. Given a standard numbering
$\delta (x)$
which represents a diagonal function D. Given a standard numbering
![]() $\xi ^+$
of
$\xi ^+$
of
![]() ${\mathcal {L}}^+$
, a diagonal function D, adequate for these choices, maps (the
${\mathcal {L}}^+$
, a diagonal function D, adequate for these choices, maps (the
![]() $\xi ^+$
-code of) an
$\xi ^+$
-code of) an
![]() ${\mathcal {L}}^+$
-formula
${\mathcal {L}}^+$
-formula
![]() $A(x)$
with x free to (the
$A(x)$
with x free to (the
![]() $\xi ^+$
-code of) its diagonalisation
$\xi ^+$
-code of) its diagonalisation
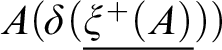 $A(\delta (\underline {\xi ^+(A)}))$
. This language extension can be achieved in different ways. Since D is primitive recursive, one may simply add a function symbol for D to
$A(\delta (\underline {\xi ^+(A)}))$
. This language extension can be achieved in different ways. Since D is primitive recursive, one may simply add a function symbol for D to
![]() ${\mathcal {L}^0}$
, or one can add function symbols for other p.r. functions such as the substitution function and the numeral function and then represent D as a complex term, etc. Let
${\mathcal {L}^0}$
, or one can add function symbols for other p.r. functions such as the substitution function and the numeral function and then represent D as a complex term, etc. Let
![]() $\mathsf {R}_{{\mathcal {L}}^+}$
be the result of adding all true equations of the form
$\mathsf {R}_{{\mathcal {L}}^+}$
be the result of adding all true equations of the form
![]() $t = \underline {n}$
to the Tarski–Mostowski–Robinson theory
$t = \underline {n}$
to the Tarski–Mostowski–Robinson theory
![]() $\mathsf {R}$
, where t is a closed
$\mathsf {R}$
, where t is a closed
![]() ${\mathcal {L}}^+$
-term. The Strong Diagonal Lemma then provides the existence of m-self-referential sentences:
${\mathcal {L}}^+$
-term. The Strong Diagonal Lemma then provides the existence of m-self-referential sentences:
Lemma 1.1. (Strong Diagonal Lemma for
 ${\mathcal {L}}^+$
)
${\mathcal {L}}^+$
)
For every
![]() ${\mathcal {L}}^+$
-formula
${\mathcal {L}}^+$
-formula
![]() $A(x)$
with x as a free variable, there exists a closed
$A(x)$
with x as a free variable, there exists a closed
![]() ${\mathcal {L}}^+$
-term t such that
${\mathcal {L}}^+$
-term t such that
 $\mathsf {R}_{{\mathcal {L}}^+} \vdash t = \underline {\xi (A(t))}$
.
$\mathsf {R}_{{\mathcal {L}}^+} \vdash t = \underline {\xi (A(t))}$
.
The second route is based on so-called self-referential Gödel numberings. A numbering
![]() $\xi $
is called self-referential if, for any formula
$\xi $
is called self-referential if, for any formula
![]() $A(x)$
, we can find a number n such that
$A(x)$
, we can find a number n such that
![]() $n = \xi (A(\underline {n}))$
. Self-referential numberings thus immediately provide m-self-referential sentences, without the need of extending the language (and the theory). The idea of self-referential Gödel numberings can be traced back to [Reference Kripke15, footnote 6] and [Reference Feferman5, p. 80]. Constructions of self-referential numberings are given in Kripke’s 1982 Princeton seminar (see footnote 1) and in his recent Reference Kripke[16], in Reference Visser, Gabbay and Guenthner[32, Reference Visser, Gabbay and Guenthner33], in Reference Heck[13] and in the Appendix of Reference Halbach and Visser[11]. The last construction is for efficient numerals: see below.
$n = \xi (A(\underline {n}))$
. Self-referential numberings thus immediately provide m-self-referential sentences, without the need of extending the language (and the theory). The idea of self-referential Gödel numberings can be traced back to [Reference Kripke15, footnote 6] and [Reference Feferman5, p. 80]. Constructions of self-referential numberings are given in Kripke’s 1982 Princeton seminar (see footnote 1) and in his recent Reference Kripke[16], in Reference Visser, Gabbay and Guenthner[32, Reference Visser, Gabbay and Guenthner33], in Reference Heck[13] and in the Appendix of Reference Halbach and Visser[11]. The last construction is for efficient numerals: see below.
The second route is typically taken to be contrived and unsatisfactory since the self-referential numberings existing in the literature to date do not satisfy certain desirable properties. One such property is monotonicity, which requires the Gödel number of an expression to be larger than the Gödel numbers of its sub-expressions. Halbach Reference Halbach[9], for instance, does not consider non-monotonic Gödel numberings as adequate formalisation choices.Footnote
3
Indeed, in the study of self-reference, monotonicity is prevalently required to hold for any reasonable or adequate numbering. It is, thus, widely believed that for adequate choices of Gödel numberings m-self-reference is not attainable in arithmetic formulated in
![]() ${\mathcal {L}^0}$
(see Reference Heck[13]). Accordingly, the natural setting to formalise self-referential reasoning is typically based on the first approach, by increasing the expressiveness of the language
${\mathcal {L}^0}$
(see Reference Heck[13]). Accordingly, the natural setting to formalise self-referential reasoning is typically based on the first approach, by increasing the expressiveness of the language
![]() ${\mathcal {L}^0}$
.
${\mathcal {L}^0}$
.
The aim of the present paper is to further investigate this trade-off between the (term-)expressiveness of the language and the naturalness of the underlying coding. In particular, we will show that the received view regarding the unattainability of m-self-reference in
![]() ${\mathcal {L}^0}$
is committed to much stronger assumptions on the coding apparatus than usually assumed in the literature.
${\mathcal {L}^0}$
is committed to much stronger assumptions on the coding apparatus than usually assumed in the literature.
We will start by investigating which requirements on Gödel numberings are sufficient to rule out self-referential numberings as admissible formalisation choices. We will first observe that when employing standard numerals, self-referential Gödel numberings indeed cannot be monotonic (see Section 3.2). Thus, by Halbach’s standards, self-referential Gödel numberings would be disqualified as adequate formalisation choices. They could be, at most, a technical tool providing an alternative proof of the Gödel Fixed Point Lemma and, thus, of the Incompleteness Theorems. (See for instance [Reference Grabmayr6, lemma 4.12].)
This is not the end of the story, however. While the attainability of m-self-referential sentences is not affected by the underlying naming device (as will become clear from inspection of Definition 3.2), we will show that the (in-)compatibility of monotonicity and self-referentiality of numberings depends crucially on this aspect of formalisation. In fact, we will show in this paper that we can produce effective self-referential monotonic numberings by basing the definition of self-referential on efficient instead of standard numerals (see Section 4 and Appendix A). That is, for any formula
![]() $A(x)$
, we can find a number n such that
$A(x)$
, we can find a number n such that
![]() $n = \xi (A(\overline {n}))$
, where
$n = \xi (A(\overline {n}))$
, where
![]() $\overline {n}$
denotes the efficient numeral of n (see Section 2.4). Setting
$\overline {n}$
denotes the efficient numeral of n (see Section 2.4). Setting
![]() $t := \overline {n}$
hence yields
$t := \overline {n}$
hence yields
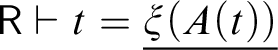 $\mathsf {R} \vdash t = \underline {\xi (A(t))}$
. The adequacy constraints on numberings have thus to be strictly more restrictive than effectiveness and monotonicity in order to rule out self-referential numberings and, in particular, m-self-referentiality in
$\mathsf {R} \vdash t = \underline {\xi (A(t))}$
. The adequacy constraints on numberings have thus to be strictly more restrictive than effectiveness and monotonicity in order to rule out self-referential numberings and, in particular, m-self-referentiality in
![]() ${\mathcal {L}^0}$
.
${\mathcal {L}^0}$
.
In Section 6, we introduce a strengthened notion of monotonicity put forward by Halbach Reference Halbach[9], which captures the idea that (efficient) numerals are arithmetical proxies for quotations. A monotonic coding is called strongly monotonic if the code of the Gödel numeral of an expression is larger than the code of the expression itself. This constraint on numberings is sufficiently restrictive to exclude self-referential numberings for any numeral system. However, we will show that even strong monotonicity is not restrictive enough to exclude m-self-referentiality, i.e., strong diagonalisation. In fact, we will construct an effective and strongly monotonic numbering which gives rise to the Strong Diagonal Lemma for
![]() $\mathcal {L}^0$
, thus providing m-self-referential sentences formulated in
$\mathcal {L}^0$
, thus providing m-self-referential sentences formulated in
![]() $\mathcal {L}^0$
.
$\mathcal {L}^0$
.
In Section 7, we introduce computational constraints which are more restrictive than effectiveness and which may serve as additional adequacy constraints for numberings. A Gödel numbering is called
![]() $\mathfrak {El}$
-adequate if it represents a large portion of syntactic relations and operations by elementary relations and operations on
$\mathfrak {El}$
-adequate if it represents a large portion of syntactic relations and operations by elementary relations and operations on
![]() $\omega $
. We show that the numberings constructed in this paper are
$\omega $
. We show that the numberings constructed in this paper are
![]() $\mathfrak {El}$
-adequate in this sense. Hence, strong monotonicity and
$\mathfrak {El}$
-adequate in this sense. Hence, strong monotonicity and
![]() $\mathfrak {El}$
-adequacy taken together, are once again not restrictive enough to exclude m-self-referentiality in
$\mathfrak {El}$
-adequacy taken together, are once again not restrictive enough to exclude m-self-referentiality in
![]() $\mathcal {L}^0$
.
$\mathcal {L}^0$
.
In Section 8, we briefly discuss the constraint of regularity on numberings for languages
![]() $\mathcal {L} \supseteq {\mathcal {L}^0}$
due to Heck Reference Heck[13]. Indeed, this constraint is sufficiently restrictive to rule out the existence of m-self-referential sentences formulated in
$\mathcal {L} \supseteq {\mathcal {L}^0}$
due to Heck Reference Heck[13]. Indeed, this constraint is sufficiently restrictive to rule out the existence of m-self-referential sentences formulated in
![]() $\mathcal {L}$
. However, we construct a decent numbering which is not regular for
$\mathcal {L}$
. However, we construct a decent numbering which is not regular for
![]() $\mathcal {L}^0$
. Regularity thus hardly serves as a necessary constraint for admissible numberings and m-self-referentiality in
$\mathcal {L}^0$
. Regularity thus hardly serves as a necessary constraint for admissible numberings and m-self-referentiality in
![]() $\mathcal {L}^0$
is in the clear.
$\mathcal {L}^0$
is in the clear.
The obtained results suggest the following disjunctive conclusion: when formalising m-self-reference in arithmetic, the adequacy constraints on reasonable numberings are more restrictive than widely assumed, or m-self-reference can be adequately formalised in a less expressive language than usually believed.Footnote
4
More specifically, we conclude that either the constraints on reasonable numberings are more restrictive than
![]() $\mathfrak {El}$
-adequacy and strong monotonicity taken together, or m-self-reference is already attainable in
$\mathfrak {El}$
-adequacy and strong monotonicity taken together, or m-self-reference is already attainable in
![]() ${\mathcal {L}^0}$
.
${\mathcal {L}^0}$
.
We close, in Section 9, by showing how these results bear on the study of axiomatic truth theories. In particular, we show that the constraints of
![]() $\mathfrak {El}$
-adequacy and (strong) monotonicity taken together are not sufficient to determine the consistency of certain type-free truth theories. Thus, the formalisation of certain informal principles of truth in an arithmetical setting is highly sensitive to the underlying formalisation choices. These results raise doubts as to what extent such axiomatic theories can be taken to faithfully reflect informal reasoning regarding the underlying principles of truth.
$\mathfrak {El}$
-adequacy and (strong) monotonicity taken together are not sufficient to determine the consistency of certain type-free truth theories. Thus, the formalisation of certain informal principles of truth in an arithmetical setting is highly sensitive to the underlying formalisation choices. These results raise doubts as to what extent such axiomatic theories can be taken to faithfully reflect informal reasoning regarding the underlying principles of truth.
Finally, we hope to provide entertaining examples of Gödel numberings which bring to light some surprising subtleties regarding the interaction between self-reference and the employed formalisation devices.
2 Technical Preliminaries
In this section, we introduce the necessary basic notions concerning syntax, theories and numberings.
2.1 Languages
Languages can be represented in many ways: as free algebras, as sets of strings, as labeled directed acyclic graphs, as … These choices are both philosophically and technically important. In our context of the study of Gödel numberings, the choice of a format for the language will often suggest a particular choice of numerical representation. E.g., labeled directed acyclic graphs can be modeled in the hereditarily finite sets and we can map these sets into numbers using the Ackermann coding. It would be very natural to base a Gödel numbering on this idea. In this paper, we will mainly employ the algebraic perspective and on the string perspective. This does not reflect a philosophical standpoint, but is just a limitation dictated by length. In Section 8.2.2, we will briefly consider the idea of sharing material in syntax.
Let
![]() $\mathcal {L}^0$
be the language of first-order arithmetic, which contains
$\mathcal {L}^0$
be the language of first-order arithmetic, which contains
![]() $\bot $
,
$\bot $
,
![]() $\top $
,
$\top $
,
![]() ${=}$
,
${=}$
,
![]() $\neg $
,
$\neg $
,
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
,
$\vee $
,
![]() ${\rightarrow }$
,
${\rightarrow }$
,
![]() $\forall $
and
$\forall $
and
![]() $\exists $
as logical constants, as well as the non-logical symbols
$\exists $
as logical constants, as well as the non-logical symbols
![]() ${\sf 0}$
,
${\sf 0}$
,
![]() $\mathsf {S}$
,
$\mathsf {S}$
,
![]() $+$
and
$+$
and
![]() $\times $
. The infix expressions of
$\times $
. The infix expressions of
![]() ${\mathcal {L}^0}$
are given as follows.
${\mathcal {L}^0}$
are given as follows.
-
•
 $x::= {\sf v} \mid x'$
$x::= {\sf v} \mid x'$
-
•
 $t ::= x \mid {\sf 0} \mid {\sf S}t \mid (t+t) \mid (t\times t)$
$t ::= x \mid {\sf 0} \mid {\sf S}t \mid (t+t) \mid (t\times t)$
-
•
 $A ::= \bot \mid \top \mid t=t \mid \neg A \mid (A \wedge A) \mid (A \vee A) \mid (A \to A) \mid \forall x\,A \mid \exists x\, A$
$A ::= \bot \mid \top \mid t=t \mid \neg A \mid (A \wedge A) \mid (A \vee A) \mid (A \to A) \mid \forall x\,A \mid \exists x\, A$
Alternatively, we will sometimes consider
![]() ${\mathcal {L}^0}$
to be given in Polish notation:
${\mathcal {L}^0}$
to be given in Polish notation:
-
•
 $x::= {\sf v} \mid x'$
$x::= {\sf v} \mid x'$
-
•
 $t ::= x \mid {\sf 0} \mid {\sf S}t \mid {\sf A} t t \mid {\sf M} t t$
$t ::= x \mid {\sf 0} \mid {\sf S}t \mid {\sf A} t t \mid {\sf M} t t$
-
•
 $A ::= \bot \mid \top \mid {=}tt \mid \neg A \mid \wedge A A \mid \vee A A \mid {\to } A A \mid \forall x\,A \mid \exists x\, A$
$A ::= \bot \mid \top \mid {=}tt \mid \neg A \mid \wedge A A \mid \vee A A \mid {\to } A A \mid \forall x\,A \mid \exists x\, A$
Let
![]() $\mathbb {N}$
be the standard interpretation of
$\mathbb {N}$
be the standard interpretation of
![]() $\mathcal {L}^0$
, with
$\mathcal {L}^0$
, with
![]() $\omega $
as its domain. In this paper, we consider arbitrary languages
$\omega $
as its domain. In this paper, we consider arbitrary languages
![]() $\mathcal {L} \supseteq {\mathcal {L}^0}$
with finite signature such that each constant symbol c and function symbol f of
$\mathcal {L} \supseteq {\mathcal {L}^0}$
with finite signature such that each constant symbol c and function symbol f of
![]() $\mathcal {L}$
has an intended interpretation
$\mathcal {L}$
has an intended interpretation
![]() $c^{\mathbb {N}}$
and
$c^{\mathbb {N}}$
and
![]() $f^{\mathbb {N}}$
in
$f^{\mathbb {N}}$
in
![]() $\mathbb {N}$
. Thus, in particular, the evaluation function
$\mathbb {N}$
. Thus, in particular, the evaluation function
![]() $\mathsf {ev}$
is well-defined on closed terms of
$\mathsf {ev}$
is well-defined on closed terms of
![]() $\mathcal {L}$
. For any such language
$\mathcal {L}$
. For any such language
![]() $\mathcal {L}$
, both definitions above extend in the obvious way. When we do not specify the employed notation system, we assume
$\mathcal {L}$
, both definitions above extend in the obvious way. When we do not specify the employed notation system, we assume
![]() $\mathcal {L}$
to be given in infix notation.
$\mathcal {L}$
to be given in infix notation.
2.2 Theories
We will mainly consider theories in the language of arithmetic. Our basic theory is be the Tarski–Mostowski–Robinson theory
![]() $\mathsf {R}$
(see [Reference Tarski, Mostowski and Robinson30, p. 53]). We will extend
$\mathsf {R}$
(see [Reference Tarski, Mostowski and Robinson30, p. 53]). We will extend
![]() $\mathsf {R}$
in a standard way to
$\mathsf {R}$
in a standard way to
![]() $\mathsf {R}_{{\mathcal {L}}}$
by adding all true equations of the form
$\mathsf {R}_{{\mathcal {L}}}$
by adding all true equations of the form
![]() $t = \underline {n}$
to
$t = \underline {n}$
to
![]() $\mathsf {R}$
, where t is a closed
$\mathsf {R}$
, where t is a closed
![]() ${\mathcal {L}}$
-term. Of course, this requires the intended interpretations of the new function symbols in the background.
${\mathcal {L}}$
-term. Of course, this requires the intended interpretations of the new function symbols in the background.
2.3 Gödel numberings
Let S be a domain which permits a robust notion of effectiveness for functions
![]() $\xi \colon S \to \omega $
.Footnote
5
We say that a function
$\xi \colon S \to \omega $
.Footnote
5
We say that a function
![]() $\xi \colon S \to \omega $
is a Gödel numbering or coding of S, if
$\xi \colon S \to \omega $
is a Gödel numbering or coding of S, if
![]() $\xi $
is injective and effective.Footnote
6
We also call
$\xi $
is injective and effective.Footnote
6
We also call
![]() $\xi (A)$
the (
$\xi (A)$
the (
![]() $\xi $
-)code of A (for terms and formulæ A). In this paper we consider numberings of languages
$\xi $
-)code of A (for terms and formulæ A). In this paper we consider numberings of languages
![]() $\mathcal {L}$
given in infix or Polish notation. We note that choice of infix language versus Polish language is, in a sense, immaterial, since the two languages/representations of the language are connected by a standard bijection.
$\mathcal {L}$
given in infix or Polish notation. We note that choice of infix language versus Polish language is, in a sense, immaterial, since the two languages/representations of the language are connected by a standard bijection.
We occasionally also consider a language as embedded in a set of strings. Then, a numbering of the strings over the given finite alphabet will induce a numbering of the language. For instance, the infix expressions of
![]() ${\mathcal {L}^0}$
can be conceived of as strings over an alphabet containing
${\mathcal {L}^0}$
can be conceived of as strings over an alphabet containing
![]() $17$
symbols, while its Polish notations can be formulated as strings over an alphabet with
$17$
symbols, while its Polish notations can be formulated as strings over an alphabet with
![]() $15$
symbols. (So, when we consider the language as embedded in strings the difference between infix and Polish suddenly does have some role.)
$15$
symbols. (So, when we consider the language as embedded in strings the difference between infix and Polish suddenly does have some role.)
We note that, e.g., if we would think of formulæ as labeled directed acyclic graphs (dags), the numbering’s domain S could be the totality of all finite labeled dags with labels in a fixed alphabet. Such choices often reflect a syntax theory. If we view syntax as sui generis, S will usually be the set of expressions itself. If we view the syntactic objects as specima of a wider variety X, we will usually take
![]() $S :=X$
.
$S :=X$
.
Remark 2.1. We could allow one extra degree of freedom for Gödel numberings: we could drop functionality. For example, suppose we want to an existing coding of syntax in the finite sets to define our Gödel numbering via coding the finite sets as numbers. There are various ways to code the finite sets. Suppose we do it by interpreting sequences first and then ignoring the order of the components. This gives us a non-functional Gödel numbering. Note that it would still be injective. For the purposes of the present paper we will not need the extra flexibility of non-functionality.
Remark 2.2. The Gödel numbering employed in Reference Feferman[4] is a nice example of a Gödel numbering that looks directly at the language-as-algebra without considering it as embedded in strings. For Feferman’s coding, the choice between infix and Polish is irrelevant.
An important example of a numbering of strings is the length-first ordering. Let
![]() ${\mathcal A}^{\ast }$
be a finite alphabet and suppose some ordering of
${\mathcal A}^{\ast }$
be a finite alphabet and suppose some ordering of
![]() ${\mathcal A}$
is given. We order the strings of
${\mathcal A}$
is given. We order the strings of
![]() ${\mathcal A}$
using the length-first ordering
${\mathcal A}$
using the length-first ordering
![]() $(\alpha _n)_{n\in \omega }$
in which we enumerate the strings according to increasing length, where the strings of same length are ordered alphabetically. We set
$(\alpha _n)_{n\in \omega }$
in which we enumerate the strings according to increasing length, where the strings of same length are ordered alphabetically. We set
![]() ${\mathfrak g}(\alpha ) = n$
if
${\mathfrak g}(\alpha ) = n$
if
![]() $\alpha = \alpha _n$
.Footnote
7
We write
$\alpha = \alpha _n$
.Footnote
7
We write
![]() $|\alpha |$
for the length of
$|\alpha |$
for the length of
![]() $\alpha $
.
$\alpha $
.
Throughout this paper, we will use the following basic fact about the length-first ordering.
Lemma 2.3. Suppose the alphabet
![]() ${\mathcal A}$
has
${\mathcal A}$
has
![]() $N \geq 2$
letters. We then have:
$N \geq 2$
letters. We then have:
 $$ \begin{align*} \frac{N^{|\alpha|}-1}{N-1} \leq {\mathfrak g} (\alpha) < \frac{N^{|\alpha|+1}-1}{N-1}. \\[-15pt]\end{align*} $$
$$ \begin{align*} \frac{N^{|\alpha|}-1}{N-1} \leq {\mathfrak g} (\alpha) < \frac{N^{|\alpha|+1}-1}{N-1}. \\[-15pt]\end{align*} $$
It follows that
![]() $|\alpha | \leq {\mathfrak g}(\alpha )$
. Moreover, whenever
$|\alpha | \leq {\mathfrak g}(\alpha )$
. Moreover, whenever
![]() $|\alpha | < |\beta |$
, then
$|\alpha | < |\beta |$
, then
![]() ${\mathfrak g}(\alpha ) < {\mathfrak g}(\beta )$
.
${\mathfrak g}(\alpha ) < {\mathfrak g}(\beta )$
.
Proof. Clearly, for any string
![]() $\alpha $
of
$\alpha $
of
![]() ${\mathcal A}$
we have
${\mathcal A}$
we have
 $$ \begin{align*} \overbrace{1\cdots 1}^{|\alpha| \times} \leq {\mathfrak g}(\alpha) \leq \overbrace{1\cdots 1}^{|\alpha|+1\; \times}, \\[-15pt]\end{align*} $$
$$ \begin{align*} \overbrace{1\cdots 1}^{|\alpha| \times} \leq {\mathfrak g}(\alpha) \leq \overbrace{1\cdots 1}^{|\alpha|+1\; \times}, \\[-15pt]\end{align*} $$
where, for any m,
 $\overbrace {1\cdots 1}^{m \times }$
is considered as an N-adic notation. The claim follows immediately from a well-known property of geometric series:
$\overbrace {1\cdots 1}^{m \times }$
is considered as an N-adic notation. The claim follows immediately from a well-known property of geometric series:
 $$ \begin{align*} \overbrace{1\cdots 1}^{m \times} = \sum_{i=0}^{m - 1} N^i = \frac{N^m-1}{N-1}. \\[-42pt]\end{align*} $$
$$ \begin{align*} \overbrace{1\cdots 1}^{m \times} = \sum_{i=0}^{m - 1} N^i = \frac{N^m-1}{N-1}. \\[-42pt]\end{align*} $$
□
2.4 Naming devices
Let
![]() $\mathsf {ClTerm}_{\mathcal {L}}$
denote the set of closed
$\mathsf {ClTerm}_{\mathcal {L}}$
denote the set of closed
![]() ${\mathcal {L}}$
-terms. We call a function
${\mathcal {L}}$
-terms. We call a function
![]() ${\nu \colon \omega \to \mathsf {ClTerm}_{\mathcal {L}}}$
a numeral function for
${\nu \colon \omega \to \mathsf {ClTerm}_{\mathcal {L}}}$
a numeral function for
![]() $\mathcal {L}$
, if
$\mathcal {L}$
, if
![]() $\nu $
is injective and effective and the closed term
$\nu $
is injective and effective and the closed term
![]() $\nu (n)$
has value n, for each
$\nu (n)$
has value n, for each
![]() $n \in \omega $
. We call
$n \in \omega $
. We call
![]() $\nu (n)$
the
$\nu (n)$
the
![]() $\nu $
-numeral of n. Standard numerals form a canonical choice of a numeral function and are defined as follows.
$\nu $
-numeral of n. Standard numerals form a canonical choice of a numeral function and are defined as follows.
-
•
 $\alpha ::= {\sf 0} \mid {\sf S}\alpha $
.
$\alpha ::= {\sf 0} \mid {\sf S}\alpha $
.
We write
![]() $\underline {n}$
for the ordinary, or standard, numeral with value n, and also write
$\underline {n}$
for the ordinary, or standard, numeral with value n, and also write
![]() $\underline {\cdot }$
for the standard numeral function. These numerals provide unique normal forms for the natural numbers. These normal forms reflect the fact that we naturally read the axioms for addition and multiplication as directed. We have
$\underline {\cdot }$
for the standard numeral function. These numerals provide unique normal forms for the natural numbers. These normal forms reflect the fact that we naturally read the axioms for addition and multiplication as directed. We have
![]() $(x+{\sf 0}) \rightsquigarrow x$
,
$(x+{\sf 0}) \rightsquigarrow x$
,
![]() $(x+{\sf S}y) \rightsquigarrow {\sf S}(x+y)$
,
$(x+{\sf S}y) \rightsquigarrow {\sf S}(x+y)$
,
![]() $(x\times {\sf 0}) \rightsquigarrow {\sf 0}$
,
$(x\times {\sf 0}) \rightsquigarrow {\sf 0}$
,
![]() $(x \times {\sf S}y) \rightsquigarrow ((x\times y)+x)$
. The numerals are the normal forms for the closed terms in this reduction system.
$(x \times {\sf S}y) \rightsquigarrow ((x\times y)+x)$
. The numerals are the normal forms for the closed terms in this reduction system.
In the literature on weak systems, however, another kind of numeral is used that corresponds to binary or dyadic notations. The main reason for this is simply that the arithmetisation of the numeral function for standard numerals and the usual Gödel numberings exhibits exponential growth. This holds for example for the Gödel numbering
![]() ${\mathfrak g}$
based on the length-first ordering. The numeral function for the numerals in the other style is more efficient. Thus, these alternative numerals are also called efficient numerals. We define efficient numerals for dyadic representations as follows.
${\mathfrak g}$
based on the length-first ordering. The numeral function for the numerals in the other style is more efficient. Thus, these alternative numerals are also called efficient numerals. We define efficient numerals for dyadic representations as follows.
-
•
 $\alpha ::= {\sf 0} \mid {\sf S}({\sf SS}{\sf 0} \times \alpha ) \mid {\sf SS}({\sf SS}{\sf 0} \times \alpha )$
.
$\alpha ::= {\sf 0} \mid {\sf S}({\sf SS}{\sf 0} \times \alpha ) \mid {\sf SS}({\sf SS}{\sf 0} \times \alpha )$
.
We write
![]() $\overline {n}$
for the efficient numeral with value n and write
$\overline {n}$
for the efficient numeral with value n and write
![]() $\overline {\cdot }$
for the efficient numeral function. We note that efficient numerals also correspond more naturally to reduction systems in a different signature, e.g., a theory of strings formulated with two successors.
$\overline {\cdot }$
for the efficient numeral function. We note that efficient numerals also correspond more naturally to reduction systems in a different signature, e.g., a theory of strings formulated with two successors.
Remark 2.4. Consider the Gödel numbering
![]() ${\mathfrak g}$
for the language
${\mathfrak g}$
for the language
![]() $\mathcal {L}^0$
based on the length-first ordering, where we assume we used infix notations. We note that the cardinality of the alphabet is 17. Consider any number n.
$\mathcal {L}^0$
based on the length-first ordering, where we assume we used infix notations. We note that the cardinality of the alphabet is 17. Consider any number n.
Clearly, we have
![]() $|\underline {n}|= n+1$
. So,
$|\underline {n}|= n+1$
. So,
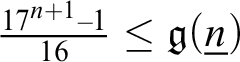 $\frac {17^{n+1}-1}{16} \leq {\mathfrak g}(\underline {n})$
. So
$\frac {17^{n+1}-1}{16} \leq {\mathfrak g}(\underline {n})$
. So
![]() ${\mathfrak g}(\underline {n})$
has an exponential lower bound in n.
${\mathfrak g}(\underline {n})$
has an exponential lower bound in n.
We give an upper bound for
![]() ${\mathfrak g}(\overline {n})$
. Let the length of the dyadic notation of n be k. We have:
${\mathfrak g}(\overline {n})$
. Let the length of the dyadic notation of n be k. We have:
![]() $ 2^k-1 \leq n < 2^{k+1}-1$
. We can estimate the length of the dyadic numeral
$ 2^k-1 \leq n < 2^{k+1}-1$
. We can estimate the length of the dyadic numeral
![]() $\overline {n}$
by considering the worst case where the dyadic notation of n is a string of 2’s. We find that
$\overline {n}$
by considering the worst case where the dyadic notation of n is a string of 2’s. We find that
![]() $|\overline {n}| \leq 8k+1$
. Thus, using that
$|\overline {n}| \leq 8k+1$
. Thus, using that
![]() $17<2^5$
, we see that:
$17<2^5$
, we see that:
 $$ \begin{align*} {\mathfrak g}(\overline{n}) < \frac{17^{8k+2} -1}{16} \leq 64\cdot 2^{40k} \leq 64\cdot (n+1)^{40}. \end{align*} $$
$$ \begin{align*} {\mathfrak g}(\overline{n}) < \frac{17^{8k+2} -1}{16} \leq 64\cdot 2^{40k} \leq 64\cdot (n+1)^{40}. \end{align*} $$
So, we see that
![]() $ {\mathfrak g}(\overline {n})$
has a polynomial upper bound in n.
$ {\mathfrak g}(\overline {n})$
has a polynomial upper bound in n.
3 Formalisations of m-Self-Reference
The notion of self-reference considered here is defined by means of a reference relation on sentences. According to Leitgeb Reference Leitgeb[17], “a singular sentence might […] be defined to refer to all the referents of all of its singular terms, and only to them” (p. 4). A sentence is then said to be self-referential if and only if it refers to itself. By employing a Gödel numbering, this notion of self-reference can be formalised in an arithmetical framework according to the following definition.Footnote 8
Definition 3.1. A sentence of the form
![]() $A(t)$
is called m-self-referential with respect to the formula
$A(t)$
is called m-self-referential with respect to the formula
![]() $A(x)$
, if the closed term t denotes (the code of)
$A(x)$
, if the closed term t denotes (the code of)
![]() $A(t)$
.
$A(t)$
.
This notion of self-reference is for example captured by the Kreisel–Henkin Criterion for self-reference (see [Reference Halbach and Visser10, p. 684]). According to this criterion, given a formula
![]() $A(x)$
expressing a property P, a sentence
$A(x)$
expressing a property P, a sentence
![]() $A(t)$
says of itself that it has property P iff
$A(t)$
says of itself that it has property P iff
![]() $A(t)$
is m-self-referential with respect to
$A(t)$
is m-self-referential with respect to
![]() $A(x)$
(in the sense of the above definition).
$A(x)$
(in the sense of the above definition).
In order to make this notion of m-self-reference mathematically precise, Definition 3.1 has to be specified with respect to the formalisation choices (i)–(iii). Accordingly, we call a triple
![]() $\langle \mathcal {L}, \xi , \nu \rangle $
a formalisation choice, if
$\langle \mathcal {L}, \xi , \nu \rangle $
a formalisation choice, if
-
•
 $\mathcal {L}$
is a language as specified in Section 2.1;
$\mathcal {L}$
is a language as specified in Section 2.1; -
•
 $\xi $
is a Gödel numbering of
$\xi $
is a Gödel numbering of
 $\mathcal {L}$
; and
$\mathcal {L}$
; and -
•
 $\nu $
is a numeral function for
$\nu $
is a numeral function for
 $\mathcal {L}$
.
$\mathcal {L}$
.
Definition 3.2. We say that m-self-reference is attainable for a formalisation choice
![]() $\langle \mathcal {L}, \xi , \nu \rangle $
, if for each
$\langle \mathcal {L}, \xi , \nu \rangle $
, if for each
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $A(x)$
there exists a closed
$A(x)$
there exists a closed
![]() $\mathcal {L}$
-term t such that
$\mathcal {L}$
-term t such that
![]() ${\mathsf {R}_{\mathcal {L}} \vdash t = \nu (\xi (A(t)))}$
.Footnote
9
${\mathsf {R}_{\mathcal {L}} \vdash t = \nu (\xi (A(t)))}$
.Footnote
9
It is easy to see that the attainability of m-self-reference is invariant regarding the choice of the numeral function. That is, m-self-reference is attainable for
![]() $\langle \mathcal {L}, \xi , \nu _1 \rangle $
iff m-self-reference is attainable for
$\langle \mathcal {L}, \xi , \nu _1 \rangle $
iff m-self-reference is attainable for
![]() $\langle \mathcal {L}, \xi , \nu _2 \rangle $
, for any language
$\langle \mathcal {L}, \xi , \nu _2 \rangle $
, for any language
![]() $\mathcal {L}$
, numbering
$\mathcal {L}$
, numbering
![]() $\xi $
and numeral functions
$\xi $
and numeral functions
![]() $\nu _1$
and
$\nu _1$
and
![]() $\nu _2$
for
$\nu _2$
for
![]() $\mathcal {L}$
. Hence, instead of requiring the provability of
$\mathcal {L}$
. Hence, instead of requiring the provability of
![]() $t = \nu (\xi (A(t)))$
in Definition 3.2, one may equivalently require that
$t = \nu (\xi (A(t)))$
in Definition 3.2, one may equivalently require that
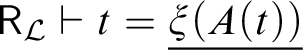 ${\mathsf {R}_{\mathcal {L}} \vdash t = \underline {\xi (A(t))}}$
. The reason for considering arbitrary numeral functions as parameters in formalisation choices is that certain adequacy conditions on numberings will be shown to be sensitive to this aspect of formalisation.
${\mathsf {R}_{\mathcal {L}} \vdash t = \underline {\xi (A(t))}}$
. The reason for considering arbitrary numeral functions as parameters in formalisation choices is that certain adequacy conditions on numberings will be shown to be sensitive to this aspect of formalisation.
Moreover, instead of using provability in
![]() $\mathsf {R}_{\mathcal {L}}$
, one can equivalently require in Definition 3.2 that
$\mathsf {R}_{\mathcal {L}}$
, one can equivalently require in Definition 3.2 that
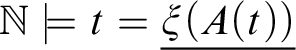 $\mathbb {N} \models t = \underline {\xi (A(t))}$
, since
$\mathbb {N} \models t = \underline {\xi (A(t))}$
, since
![]() $\mathsf {R}_{\mathcal {L}}$
proves every true equation of closed
$\mathsf {R}_{\mathcal {L}}$
proves every true equation of closed
![]() $\mathcal {L}$
-terms.
$\mathcal {L}$
-terms.
3.1 Adequacy of formalisation
In formal studies of truth, self-reference and the semantic paradoxes, it is common practice to employ natural numbers as theoretical proxies for syntactic expressions. Accordingly, certain designated arithmetical domains or theories serve as domains of expressions or syntax theories respectively. This practice of arithmetisation rests on Gödel numberings, which can be seen as translation devices between expressions and numbers. However, as a consequence of intensionality phenomena in metamathematics, not every numbering, i.e., injective and effective function, can be considered an equally adequate candidate.
When formalising notions such as truth or (self-)reference over an arithmetical domain or theory, it is therefore essential that the underlying Gödel numbering constitutes an adequate translation device between expressions and numbers. Only then are we justified in considering the given arithmetical framework a domain or theory of expressions and in taking the formalised notions to apply to linguistic expressions as intended. In order to guarantee a faithful formalisation of the given philosophical notions, adequate choices of formalisation are thus required.
It is notoriously difficult to precisely characterise the notion of adequacy for numberings for a given metamathematical or philosophical purpose. We will therefore adopt a more modest approach in this paper by discussing certain necessary conditions for adequate numberings which can be found in the literature on self-reference and axiomatic truth theories.
3.1.1 Monotonicity
Perhaps, the most prominent adequacy constraint is monotonicity. Let S be a set and let
![]() $\vartriangleleft $
be a strict partial order relation on S. A Gödel numbering
$\vartriangleleft $
be a strict partial order relation on S. A Gödel numbering
![]() $\xi $
of S is called monotonic with respect to
$\xi $
of S is called monotonic with respect to
![]() $\vartriangleleft $
, if
$\vartriangleleft $
, if
![]() $\alpha \vartriangleleft \beta $
implies
$\alpha \vartriangleleft \beta $
implies
![]() $\xi (\alpha ) < \xi (\beta )$
, for all
$\xi (\alpha ) < \xi (\beta )$
, for all
![]() $\alpha , \beta \in S$
. Let
$\alpha , \beta \in S$
. Let
![]() $\mathcal {L}$
be a language given in infix or Polish notion (see Section 2.1). We call a numbering
$\mathcal {L}$
be a language given in infix or Polish notion (see Section 2.1). We call a numbering
![]() $\xi $
of
$\xi $
of
![]() $\mathcal {L}$
monotonic, if it is monotonic with respect to the strict sub-expression relation
$\mathcal {L}$
monotonic, if it is monotonic with respect to the strict sub-expression relation
![]() $\prec $
given on infix or Polish notations respectively. Monotonicity in this context can therefore be equivalently characterised by requiring a numbering
$\prec $
given on infix or Polish notations respectively. Monotonicity in this context can therefore be equivalently characterised by requiring a numbering
![]() $\xi $
of
$\xi $
of
![]() $\mathcal {L}$
to satisfy the following three conditions:
$\mathcal {L}$
to satisfy the following three conditions:
-
M1. for all
 $\mathcal {L}$
-terms
$\mathcal {L}$
-terms
 $s,t$
, if
$s,t$
, if
 $s \prec t$
then
$s \prec t$
then
 $\xi (s) < \xi (t)$
;
$\xi (s) < \xi (t)$
; -
M2. for all
 $\mathcal {L}$
-formulæ
$\mathcal {L}$
-formulæ
 $A, B$
, if
$A, B$
, if
 $A \prec B$
then
$A \prec B$
then
 $\xi (A) < \xi (B)$
; and
$\xi (A) < \xi (B)$
; and -
M3. for all
 $\mathcal {L}$
-terms s and formulæ A, if
$\mathcal {L}$
-terms s and formulæ A, if
 $s \prec A$
then
$s \prec A$
then
 $\xi (s) < \xi (A)$
.
$\xi (s) < \xi (A)$
.
Thus, when we consider numberings of well-formed expressions, we do not demand monotonicity with respect to sub-strings. E.g., in case
![]() $\xi ((A \wedge B))$
would be
$\xi ((A \wedge B))$
would be
![]() ${\langle 7,{\langle \xi (A),\xi (B) \rangle } \rangle }$
, where
${\langle 7,{\langle \xi (A),\xi (B) \rangle } \rangle }$
, where
![]() ${\langle \cdot ,\cdot \rangle }$
is the Cantor Pairing, the brackets do not appear in the code, so we do not need a Gödel number for a bracket. However, when considering numberings of strings, monotonicity may be also required with respect to the (strict) sub-string relation. Clearly, any numbering which is monotonic in this sense also satisfies the conditions M1–M3.
${\langle \cdot ,\cdot \rangle }$
is the Cantor Pairing, the brackets do not appear in the code, so we do not need a Gödel number for a bracket. However, when considering numberings of strings, monotonicity may be also required with respect to the (strict) sub-string relation. Clearly, any numbering which is monotonic in this sense also satisfies the conditions M1–M3.
Halbach Reference Halbach[9] for instance does not consider non-monotonic Gödel numerings as adequate formalisation choices. Indeed, the study of self-reference is typically based on numberings which are required to be monotonic. This requirement is explicit for instance in [Reference Milne19, footnote 4], [Reference Halbach8, p. 33], [Reference Picollo21, pp. 573f.], [Reference Picollo22, footnote 4] and [Reference Picollo23, footnote 3] (where Milne requires monotonicity with respect to the sub-string relation). A good example of an application of (a strengthened version of) monotonicity is the proof of the falsity of the
![]() $\Sigma ^0_1$
-truth teller for fixed-point operators with certain good properties. See [Reference Halbach and Visser11, theorem 7.7].
$\Sigma ^0_1$
-truth teller for fixed-point operators with certain good properties. See [Reference Halbach and Visser11, theorem 7.7].
One way to motivate this constraint as a necessary condition of adequacy for numberings proceeds as follows. Let
![]() $\leq $
be the usual less-than (or equal) relation on numbers and let
$\leq $
be the usual less-than (or equal) relation on numbers and let
![]() $\preceq $
denote the sub-expression relation on the given domain
$\preceq $
denote the sub-expression relation on the given domain
![]() $\mathcal {L}$
of expressions. One may conceive of
$\mathcal {L}$
of expressions. One may conceive of
![]() $\preceq $
as a parthood relation on
$\preceq $
as a parthood relation on
![]() $\mathcal {L}$
. One may endow
$\mathcal {L}$
. One may endow
![]() $\leq $
with such a mereological interpretation by representing numbers as strings of strokes. Another approach is to represent numbers as Von Neumann ordinals, and to understand the parthood relation on sets as the containment relation
$\leq $
with such a mereological interpretation by representing numbers as strings of strokes. Another approach is to represent numbers as Von Neumann ordinals, and to understand the parthood relation on sets as the containment relation
![]() $\subseteq $
(see e.g., Reference Lewis[18]). Then
$\subseteq $
(see e.g., Reference Lewis[18]). Then
![]() $\leq $
is indeed a parthood relation on numbers.Footnote
10
Taking parthood as an important structural feature of the domain of expressions, adequate numberings may then be required to preserve structure in virtue of representing the parthood relation
$\leq $
is indeed a parthood relation on numbers.Footnote
10
Taking parthood as an important structural feature of the domain of expressions, adequate numberings may then be required to preserve structure in virtue of representing the parthood relation
![]() $\preceq $
on
$\preceq $
on
![]() $\mathcal {L}$
by a relation on
$\mathcal {L}$
by a relation on
![]() $\omega $
contained in the parthood relation
$\omega $
contained in the parthood relation
![]() $\leq $
on numbers, which is tantamount to requiring monotonicity. We will introduce further adequacy conditions for numberings in later sections of this paper.
$\leq $
on numbers, which is tantamount to requiring monotonicity. We will introduce further adequacy conditions for numberings in later sections of this paper.
3.1.2 Numerals
Thus far, we have only discussed adequacy with respect to Gödel numberings. It remains to be clarified which numeral functions constitute adequate formalisation choices. One approach is to characterise a numeral function as adequate iff it corresponds to an acceptable or canonical naming system for the natural numbers (see [Reference Horsten14, Reference Shapiro27]). Note that on this approach, standard numerals as well as efficient numerals qualify as adequate numeral systems.
One way to view the natural numbers is as the free algebra for a unary function and one generator. Addition and multiplication are, then, defined by recursion, where the possibility of such recursions is guaranteed by the fact that we have a free algebra. From this point of view, the standard or tally numbers indeed seem to have a preferred status: they are the standard syntactic representations of the elements of the free algebra. However, we would like to point out that the point of view of this specific free algebra is not the only way to think of the natural numbers. In a sense, viewing the natural numbers as this free algebra is taking the tally numerals to be the basic numerals. Alternatively, we could take the dyadic representation to be primary and work with a theory with two successors. In such a context, the dyadic numerals would be the usual syntactic representations. Similarly, the notion of natural number as finite cardinal does not automatically dictate zero and successor to be the preferred signature.
We will not deal with the question of the status of numerals in this paper and simply assume that both standard numerals as well as efficient numerals are adequate choices of a naming device. For a further discussion the reader is referred to Reference Auerbach[1].
3.2 Monotonicity and self-referentiality
The notion of self-referential numberings can be generalised to arbitrary numeral functions.
Definition 3.3. A numbering
![]() $\xi $
is called self-referential for a numeral function
$\xi $
is called self-referential for a numeral function
![]() $\nu $
if, for any formula
$\nu $
if, for any formula
![]() $A(x)$
, there exists
$A(x)$
, there exists
![]() $n \in \omega $
such that
$n \in \omega $
such that
![]() $n=\xi ( A(\nu (n)) )$
.
$n=\xi ( A(\nu (n)) )$
.
As opposed to the notion of m-self-reference for sentences (see Definition 3.1), self-reference for numberings is a mere technical concept and not intended to capture a pre-theoretical or philosophical notion. However, as we have seen, self-referential numberings immediately yield m-self-referential sentences.
In the following sections we will investigate whether adequate numberings can be self-referential, i.e., whether self-referential numberings are indeed as contrived as typically believed. We will first examine whether monotonicity serves as an adequacy condition on numberings which is sufficiently restrictive to exclude self-referential numberings and will then turn to additional more restrictive adequacy constraints for numberings.
We start by showing that a monotonic numbering cannot be self-referential for a numeral function
![]() $\nu $
, if the number of subterms of
$\nu $
, if the number of subterms of
![]() $\nu (n)$
grows sufficiently fast. In order to make this precise, let
$\nu (n)$
grows sufficiently fast. In order to make this precise, let
![]() $\mathsf {st} \colon \mathsf {ClTerm}_{\mathcal {L}} \to \omega $
be the function assigning to each closed
$\mathsf {st} \colon \mathsf {ClTerm}_{\mathcal {L}} \to \omega $
be the function assigning to each closed
![]() $\mathcal {L}$
-term the number of its proper subterms-qua-type. We then get the following incompatibility result.
$\mathcal {L}$
-term the number of its proper subterms-qua-type. We then get the following incompatibility result.
Lemma 3.4. Let
![]() $\nu $
be a numeral function and suppose that there is a constant
$\nu $
be a numeral function and suppose that there is a constant
![]() $c \in \omega $
such that
$c \in \omega $
such that
![]() ${\sf st}(\nu(n))< c$
, for all
${\sf st}(\nu(n))< c$
, for all
![]() $n \in \omega $
. Then, there is no monotonic numbering which is self-referential for
$n \in \omega $
. Then, there is no monotonic numbering which is self-referential for
![]() $\nu $
.
$\nu $
.
Proof. Assume that
![]() $\xi $
is monotonic and self-referential for
$\xi $
is monotonic and self-referential for
![]() $\nu $
. Let
$\nu $
. Let
![]() $B(x)$
be an
$B(x)$
be an
![]() $\mathcal {L}$
-formula in which x does occur freely at least once. Set
$\mathcal {L}$
-formula in which x does occur freely at least once. Set
 $$ \begin{align*} A(x) := \underbrace{B(x) \vee \cdots \vee B(x)}_{(c+1) \times}. \end{align*} $$
$$ \begin{align*} A(x) := \underbrace{B(x) \vee \cdots \vee B(x)}_{(c+1) \times}. \end{align*} $$
Then there exists
![]() $n \in \omega $
such that
$n \in \omega $
such that
![]() $\xi (A(\nu (n))) = n$
. By monotonicity we then get
$\xi (A(\nu (n))) = n$
. By monotonicity we then get
 $$ \begin{align*} n & = \xi(A(\nu(n)))\\ & = \xi(\underbrace{B(\nu(n)) \vee \cdots \vee B(\nu(n))}_{(c+1) \times})\\ & \geq \xi(\underbrace{B(\nu(n)) \vee \cdots \vee B(\nu(n))}_{c \times}) +1 \geq \cdots\\ & \geq \xi(B(\nu(n))) + c\\ & \geq \xi(\nu(n)) +c\\ & \geq \mathsf{st}(\nu(n)) + c, \end{align*} $$
$$ \begin{align*} n & = \xi(A(\nu(n)))\\ & = \xi(\underbrace{B(\nu(n)) \vee \cdots \vee B(\nu(n))}_{(c+1) \times})\\ & \geq \xi(\underbrace{B(\nu(n)) \vee \cdots \vee B(\nu(n))}_{c \times}) +1 \geq \cdots\\ & \geq \xi(B(\nu(n))) + c\\ & \geq \xi(\nu(n)) +c\\ & \geq \mathsf{st}(\nu(n)) + c, \end{align*} $$
in contradiction to the assumption that
![]() $n - \mathsf {st}(\nu (n)) < c$
.□
$n - \mathsf {st}(\nu (n)) < c$
.□
Since
![]() $n - \mathsf {st}(\underline {n}) < 1$
for all
$n - \mathsf {st}(\underline {n}) < 1$
for all
![]() $n \in \omega $
, we conclude from the above lemma:
$n \in \omega $
, we conclude from the above lemma:
Corollary 3.5. There is no self-referential numbering for standard numerals which is monotonic.
After the second author’s lecture on Cogwheels of Self-reference at the workshop Ouroboros, Formal Criteria of Self-Reference in Mathematics and Philosophy on February 17, 2018, Joel Hamkins asked whether the result on the non-monotonicity of self-referential Gödel numberings also holds when we consider efficient numerals.
We first note that Lemma 3.4 does not apply to efficient numerals. We define:
-
•
 $\widetilde 0 := {\sf 0}$
and
$\widetilde 0 := {\sf 0}$
and -
•
 $\widetilde {n+1} := {\sf S}({\sf SS}{\sf 0} \times \widetilde {n})$
.
$\widetilde {n+1} := {\sf S}({\sf SS}{\sf 0} \times \widetilde {n})$
.
Let ev be the evaluation function for arithmetical closed terms and let
![]() $|\alpha |$
denote the length of the string
$|\alpha |$
denote the length of the string
![]() $\alpha $
. We find:
$\alpha $
. We find:
Lemma 3.6. For every
![]() $n \in \omega $
$n \in \omega $
-
•
 ${\sf ev}(\widetilde {n} ) = 2^n -1$
;
${\sf ev}(\widetilde {n} ) = 2^n -1$
; -
•
 $|\widetilde {n}| = 7n+1$
; and
$|\widetilde {n}| = 7n+1$
; and -
• the number of subterms-qua-type of
 $\widetilde {n}$
is
$\widetilde {n}$
is
 $\leq 2n+3$
.
$\leq 2n+3$
.
From this lemma we conclude that the function
![]() $\lambda n.2^n -1$
grows exponentially while the number of subterms of
$\lambda n.2^n -1$
grows exponentially while the number of subterms of
![]() $\overline {2^n -1}$
is not larger than
$\overline {2^n -1}$
is not larger than
![]() $2n+3$
and thus only grows linearly. Hence, the assumption of Lemma 3.4 cannot be satisfied for efficient numerals, since there is no constant c such that
$2n+3$
and thus only grows linearly. Hence, the assumption of Lemma 3.4 cannot be satisfied for efficient numerals, since there is no constant c such that
![]() $n - {\sf st}(\overline {n}) < c$
for all
$n - {\sf st}(\overline {n}) < c$
for all
![]() $n \in \omega $
.
$n \in \omega $
.
Indeed, in what follows we show that the answer to Hamkins’ question is no, by constructing a monotonic numbering which is self-referential for efficient numerals.
4 A Monotonic Self-Referential Numbering
Let
![]() ${\mathcal L}$
be an arithmetical language, as introduced in Section 2.1, and let
${\mathcal L}$
be an arithmetical language, as introduced in Section 2.1, and let
![]() ${\mathcal L}(\mathsf {c})$
be
${\mathcal L}(\mathsf {c})$
be
![]() ${\mathcal L}$
extended with a fresh constant
${\mathcal L}$
extended with a fresh constant
![]() $\mathsf {c}$
. Let
$\mathsf {c}$
. Let
![]() $A_0,A_1,\dots $
be an effective enumeration of all expressions of
$A_0,A_1,\dots $
be an effective enumeration of all expressions of
![]() ${\mathcal L}(\mathsf {c})$
. We assume that if
${\mathcal L}(\mathsf {c})$
. We assume that if
![]() $C \preceq A_n$
, then, for some
$C \preceq A_n$
, then, for some
![]() $k\leq n$
, we have
$k\leq n$
, we have
![]() $C=A_k$
.
$C=A_k$
.
We define
![]() ${\lceil A \rceil }$
as the number of sub-expressions-qua-type of A, in other words,
${\lceil A \rceil }$
as the number of sub-expressions-qua-type of A, in other words,
![]() ${\lceil A \rceil } $
is the cardinality of
${\lceil A \rceil } $
is the cardinality of
![]() $\{ B\mid B\preceq A \}$
. The following trivial observation is very useful:
$\{ B\mid B\preceq A \}$
. The following trivial observation is very useful:
Lemma 4.1.
![]() ${\lceil A_k \rceil } \leq k+1$
.
${\lceil A_k \rceil } \leq k+1$
.
Let
![]() $A [{\sf c} := t]$
denote the result of substituting t for all occurrences of
$A [{\sf c} := t]$
denote the result of substituting t for all occurrences of
![]() ${\sf c}$
in A. Here is our construction.
${\sf c}$
in A. Here is our construction.
We construct a list
![]() $\Lambda :=(B_n)_{n\in \omega }$
in stages k. Let
$\Lambda :=(B_n)_{n\in \omega }$
in stages k. Let
![]() ${\mathfrak n}(k) := 2^{k+4}+1$
. Each stage k will result in a list
${\mathfrak n}(k) := 2^{k+4}+1$
. Each stage k will result in a list
![]() $\Lambda _k = B_0,\dots , B_{{\mathfrak n}(k)-1}$
. To simplify the presentation, we make
$\Lambda _k = B_0,\dots , B_{{\mathfrak n}(k)-1}$
. To simplify the presentation, we make
![]() $\Lambda _{-1}$
the empty list and
$\Lambda _{-1}$
the empty list and
![]() ${\mathfrak n}(-1) := 0$
.
${\mathfrak n}(-1) := 0$
.
In stage k, we act as follows. Let
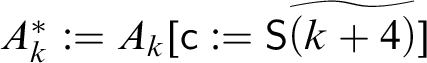 $A_k^{\ast } := A_k [{\sf c} := {\sf S}\widetilde {(k+4)}]$
. Let the sub-expressions of
$A_k^{\ast } := A_k [{\sf c} := {\sf S}\widetilde {(k+4)}]$
. Let the sub-expressions of
![]() $A_k^{\ast }$
that do not occur in
$A_k^{\ast }$
that do not occur in
![]() $\Lambda _{k-1}$
and are not of the form
$\Lambda _{k-1}$
and are not of the form
![]() $\underline {m}$
be
$\underline {m}$
be
![]() $A_{i_0},\dots , A_{i_{\ell -1}}$
, where the sequence
$A_{i_0},\dots , A_{i_{\ell -1}}$
, where the sequence
![]() $i_j$
is strictly increasing. We note that
$i_j$
is strictly increasing. We note that
![]() $\ell $
could be 0. We define
$\ell $
could be 0. We define
![]() $B_{{\mathfrak n}(k)-\ell +j} := A_{i_j}$
, for
$B_{{\mathfrak n}(k)-\ell +j} := A_{i_j}$
, for
![]() $j <\ell $
. Let s be the smallest number such that
$j <\ell $
. Let s be the smallest number such that
![]() $\underline s$
is not in
$\underline s$
is not in
![]() $\Lambda _{k-1}$
. We set
$\Lambda _{k-1}$
. We set
![]() $B_{{\mathfrak n}(k-1)+p} := \underline {s+p}$
, for
$B_{{\mathfrak n}(k-1)+p} := \underline {s+p}$
, for
![]() $p< {\mathfrak n}(k)-{\mathfrak n}(k-1)-\ell $
.
$p< {\mathfrak n}(k)-{\mathfrak n}(k-1)-\ell $
.
The construction in stage k of the list
![]() $\Lambda _k$
can be illustrated as follows:
$\Lambda _k$
can be illustrated as follows:

It follows from the construction that if
![]() $A^{\ast }_k$
is not in
$A^{\ast }_k$
is not in
![]() $\Lambda _{k-1}$
, then
$\Lambda _{k-1}$
, then
 $$ \begin{align} B_{{\mathfrak n}(k)-1} = A_k^{\ast} = A_k[\mathsf{c} := \mathsf{S}(\widetilde{k+4})]. \end{align} $$
$$ \begin{align} B_{{\mathfrak n}(k)-1} = A_k^{\ast} = A_k[\mathsf{c} := \mathsf{S}(\widetilde{k+4})]. \end{align} $$
We will show in Lemma 4.6 that (1) holds for each
![]() $A_k$
which contains
$A_k$
which contains
![]() $\mathsf {c}$
.
$\mathsf {c}$
.
To see that our construction is well-defined it is sufficient that
![]() ${\mathfrak n}(k)-\ell \geq {\mathfrak n}(k-1)$
or, equivalently,
${\mathfrak n}(k)-\ell \geq {\mathfrak n}(k-1)$
or, equivalently,
![]() $\ell \leq {\mathfrak n}(k)-{\mathfrak n}(k-1)$
. We note that:
$\ell \leq {\mathfrak n}(k)-{\mathfrak n}(k-1)$
. We note that:
 $$ \begin{align*} \ell \leq {\lceil A_k^{\ast} \rceil} \leq {\lceil A_k \rceil}+{\lceil {\sf S}\widetilde {(k+4)} \rceil}-1 \leq k +1 + 2(k+4)+3 = 3 k + 12. \end{align*} $$
$$ \begin{align*} \ell \leq {\lceil A_k^{\ast} \rceil} \leq {\lceil A_k \rceil}+{\lceil {\sf S}\widetilde {(k+4)} \rceil}-1 \leq k +1 + 2(k+4)+3 = 3 k + 12. \end{align*} $$
(The
![]() $-1$
in the right-hand-side of the second inequality can be seen as follows. In case c occurs in
$-1$
in the right-hand-side of the second inequality can be seen as follows. In case c occurs in
![]() $A_k$
it is subtracted in the substitution. If c does not occur, we have
$A_k$
it is subtracted in the substitution. If c does not occur, we have
![]() $A_k = A_k^{\ast }$
and, from this, the inequality follows immediately.)
$A_k = A_k^{\ast }$
and, from this, the inequality follows immediately.)
If
![]() $k=0$
, we have
$k=0$
, we have
![]() $3\cdot 0 +12 = 12 < 17 = 2^{0+4}+1-0 = {\mathfrak n}(0) - {\mathfrak n}(-1)$
. Let
$3\cdot 0 +12 = 12 < 17 = 2^{0+4}+1-0 = {\mathfrak n}(0) - {\mathfrak n}(-1)$
. Let
![]() $k>0$
. We find:
$k>0$
. We find:
Lemma 4.2. Suppose
![]() $A_k \in {\mathcal L}$
. Then,
$A_k \in {\mathcal L}$
. Then,
![]() $A_k$
is in
$A_k$
is in
![]() $\Lambda _k$
and, hence, in
$\Lambda _k$
and, hence, in
![]() $\Lambda $
.
$\Lambda $
.
Proof. Consider stage k. We note that
![]() $A_k^{\ast } = A_k$
. In case
$A_k^{\ast } = A_k$
. In case
![]() $A_k$
occurs in
$A_k$
occurs in
![]() $\Lambda _{k-1}$
, we are done. In case
$\Lambda _{k-1}$
, we are done. In case
![]() $A_k$
is not in
$A_k$
is not in
![]() $\Lambda _{k-1}$
and not of the form
$\Lambda _{k-1}$
and not of the form
![]() $\underline {m}$
, clearly,
$\underline {m}$
, clearly,
![]() $A_k$
will be added, so we are again done. Suppose
$A_k$
will be added, so we are again done. Suppose
![]() $A_k = \underline {m}$
, for some m. It follows that
$A_k = \underline {m}$
, for some m. It follows that
![]() $m+1={\lceil \underline {m} \rceil } \leq k+1$
. We note that all sub-expressions of
$m+1={\lceil \underline {m} \rceil } \leq k+1$
. We note that all sub-expressions of
![]() $A_k$
are all of the form
$A_k$
are all of the form
![]() $\underline {m}'$
, for
$\underline {m}'$
, for
![]() $m'\leq m$
. So
$m'\leq m$
. So
![]() $\ell = 0$
. Clearly,
$\ell = 0$
. Clearly,
![]() $m+1 \leq k+1 < {\mathfrak n}(k) - {\mathfrak n}(k-1)$
. So, all sub-expressions of
$m+1 \leq k+1 < {\mathfrak n}(k) - {\mathfrak n}(k-1)$
. So, all sub-expressions of
![]() $A_k$
are either in
$A_k$
are either in
![]() $\Lambda _{k-1}$
or will be added.□
$\Lambda _{k-1}$
or will be added.□
Lemma 4.3. Suppose
![]() $C \preceq B_n$
. Then, for some
$C \preceq B_n$
. Then, for some
![]() $j\leq n$
, we have
$j\leq n$
, we have
![]() $C = B_j$
.
$C = B_j$
.
Proof. Let
![]() $C \preceq B_n$
. Suppose
$C \preceq B_n$
. Suppose
![]() $B_n$
is added in stage k. Then,
$B_n$
is added in stage k. Then,
![]() $B_n$
is either of the form
$B_n$
is either of the form
![]() $\underline {m}$
or a sub-expression of
$\underline {m}$
or a sub-expression of
![]() $A^{\ast }_k$
not of the form
$A^{\ast }_k$
not of the form
![]() $\underline {m}$
.
$\underline {m}$
.
Suppose
![]() $B_n = \underline {m}$
. Let s be the smallest number such that
$B_n = \underline {m}$
. Let s be the smallest number such that
![]() $\underline s$
is not in
$\underline s$
is not in
![]() $\Lambda _{k-1}$
. For all
$\Lambda _{k-1}$
. For all
![]() $s'< s$
, we have
$s'< s$
, we have
![]() $\underline s'\in \Lambda _{k-1}$
. By our construction, all
$\underline s'\in \Lambda _{k-1}$
. By our construction, all
![]() $\underline s''$
, for
$\underline s''$
, for
![]() $s\leq s''\leq m$
are added at stage k in ascending order. So, for all
$s\leq s''\leq m$
are added at stage k in ascending order. So, for all
![]() $s^{\circ } \leq m$
, we find that
$s^{\circ } \leq m$
, we find that
![]() $\underline s^{\circ }$
precedes
$\underline s^{\circ }$
precedes
![]() $\underline {m}$
in
$\underline {m}$
in
![]() $ \Lambda _k$
. Finally, each sub-expression C of
$ \Lambda _k$
. Finally, each sub-expression C of
![]() $\underline {m}$
is of the form
$\underline {m}$
is of the form
![]() $\underline s^{\circ }$
, for some
$\underline s^{\circ }$
, for some
![]() $s^{\circ } \leq m$
.
$s^{\circ } \leq m$
.
Suppose
![]() $B_n$
is added as a sub-expression of
$B_n$
is added as a sub-expression of
![]() $A^{\ast }_k$
not of the form
$A^{\ast }_k$
not of the form
![]() $\underline {m}$
. First suppose
$\underline {m}$
. First suppose
![]() $C= \underline p$
. We note that
$C= \underline p$
. We note that
![]() $p+1 = {\lceil \underline p \rceil } < {\lceil A_k \rceil } \leq k+1$
. This tells us, by Lemma 4.2, that
$p+1 = {\lceil \underline p \rceil } < {\lceil A_k \rceil } \leq k+1$
. This tells us, by Lemma 4.2, that
![]() $\underline p$
is in
$\underline p$
is in
![]() $\Lambda _{k-1}$
. Hence, it is added to
$\Lambda _{k-1}$
. Hence, it is added to
![]() $\Lambda $
before
$\Lambda $
before
![]() $B_n$
. Now suppose that C is not of the form
$B_n$
. Now suppose that C is not of the form
![]() $\underline p$
. Then either C is in
$\underline p$
. Then either C is in
![]() $\Lambda _{k-1}$
or added to
$\Lambda _{k-1}$
or added to
![]() $\Lambda _k$
before
$\Lambda _k$
before
![]() $B_n$
.□
$B_n$
.□
Lemma 4.4. The enumeration
![]() $\Lambda $
is without repetitions.
$\Lambda $
is without repetitions.
Proof. Consider any
![]() $C \in {\mathcal L}$
. If C is not of the form
$C \in {\mathcal L}$
. If C is not of the form
![]() $\underline {m}$
by our construction it will be only added once.
$\underline {m}$
by our construction it will be only added once.
Suppose
![]() $ C = \underline {m}$
. We note that, by Lemma 4.3, the n such that
$ C = \underline {m}$
. We note that, by Lemma 4.3, the n such that
![]() $\underline {n} \in \Lambda _{k-1}$
are downwards closed. This means that, in our construction, there is no
$\underline {n} \in \Lambda _{k-1}$
are downwards closed. This means that, in our construction, there is no
![]() $m\geq s$
, such that
$m\geq s$
, such that
![]() $\underline {m} \in \Lambda _{k-1}$
. So all the
$\underline {m} \in \Lambda _{k-1}$
. So all the
![]() $\underline {m}$
that are added in any stage k are new.□
$\underline {m}$
that are added in any stage k are new.□
Lemma 4.5. Suppose
![]() ${\sf S}\widetilde {n}$
occurs in
${\sf S}\widetilde {n}$
occurs in
![]() $\Lambda _k$
, then
$\Lambda _k$
, then
![]() $n \leq k+4$
.
$n \leq k+4$
.
Proof. We prove this by induction on k. In stage 0, we easily verify that the largest term of the form
![]() $\mathsf {S}\widetilde {n}$
can be at most
$\mathsf {S}\widetilde {n}$
can be at most
![]() $\mathsf {S} \widetilde {4}$
.
$\mathsf {S} \widetilde {4}$
.
Suppose, we have our desired estimate for
![]() $k-1$
, where
$k-1$
, where
![]() $k>0$
. We prove our estimate for k. Clearly, the
$k>0$
. We prove our estimate for k. Clearly, the
![]() $\mathsf {S}\widetilde {n}$
occurring in
$\mathsf {S}\widetilde {n}$
occurring in
![]() $\Lambda _{k-1}$
do satisfy our estimate. Moreover, all the
$\Lambda _{k-1}$
do satisfy our estimate. Moreover, all the
![]() $\underline p$
added in stage k do not provide new elements of the form
$\underline p$
added in stage k do not provide new elements of the form
![]() $\mathsf {S}\widetilde {n}$
. So, the only interesting case is the case where
$\mathsf {S}\widetilde {n}$
. So, the only interesting case is the case where
![]() $A_k$
is not a standard numeral. Suppose it is not. The
$A_k$
is not a standard numeral. Suppose it is not. The
![]() ${\sf S}\widetilde {n}$
that are added are all sub-expressions of
${\sf S}\widetilde {n}$
that are added are all sub-expressions of
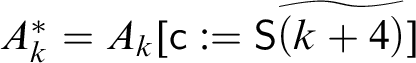 $ A^{\ast }_k= A_k[{\sf c} := {\sf S}\widetilde {(k+4)}]$
. So, we should focus on the largest such subterm. Suppose
$ A^{\ast }_k= A_k[{\sf c} := {\sf S}\widetilde {(k+4)}]$
. So, we should focus on the largest such subterm. Suppose
![]() ${\sf S}\widetilde {n} \preceq A^{\ast }_k$
. There are two possibilities:
${\sf S}\widetilde {n} \preceq A^{\ast }_k$
. There are two possibilities:
-
i.
 ${\sf S}\widetilde {n}\preceq A_k$
. In this case, we have
${\sf S}\widetilde {n}\preceq A_k$
. In this case, we have
 $n < {\lceil \mathsf {S}\widetilde {n} \rceil } \leq {\lceil A_k \rceil } \leq k+1 \leq k +4$
.
$n < {\lceil \mathsf {S}\widetilde {n} \rceil } \leq {\lceil A_k \rceil } \leq k+1 \leq k +4$
. -
ii.
 $n= k+4$
, since the subterm results from the substitution for c.
$n= k+4$
, since the subterm results from the substitution for c.
In each of the possible cases, we are done.□
Lemma 4.6. Consider any A such that c occurs in A. Then, for some n,
![]() $B_n = A[{\sf c}:= \overline {n}]$
.
$B_n = A[{\sf c}:= \overline {n}]$
.
Proof. Suppose c occurs in A. Let
![]() $A := A_k$
. The only thing we have to show is that
$A := A_k$
. The only thing we have to show is that
![]() $A^{\ast }_k$
is not in
$A^{\ast }_k$
is not in
![]() $\Lambda _{k-1}$
. This is certainly true for
$\Lambda _{k-1}$
. This is certainly true for
![]() $k=0$
. Suppose
$k=0$
. Suppose
![]() $k>0$
. We note that
$k>0$
. We note that
 ${\sf S}\widetilde {(k+4)}$
occurs in
${\sf S}\widetilde {(k+4)}$
occurs in
![]() $A^{\ast }_k$
. So, it is sufficient to show that
$A^{\ast }_k$
. So, it is sufficient to show that
 ${\sf S}\widetilde {(k+4)}$
does not occur in
${\sf S}\widetilde {(k+4)}$
does not occur in
![]() $\Lambda _{k-1}$
. By Lemma 4.5, whenever
$\Lambda _{k-1}$
. By Lemma 4.5, whenever
![]() $\mathsf {S}\widetilde {n}$
occurs in
$\mathsf {S}\widetilde {n}$
occurs in
![]() $\Lambda _{k-1}$
, we have
$\Lambda _{k-1}$
, we have
![]() $n \leq k+3$
. We may conclude that
$n \leq k+3$
. We may conclude that
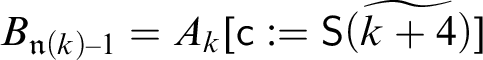 $B_{{\mathfrak n}(k)-1} = A_k[\mathsf {c} := \mathsf {S}(\widetilde {k+4})]$
. Let
$B_{{\mathfrak n}(k)-1} = A_k[\mathsf {c} := \mathsf {S}(\widetilde {k+4})]$
. Let
![]() $n := {\mathfrak n}(k)-1$
. Since
$n := {\mathfrak n}(k)-1$
. Since
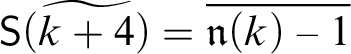 $\mathsf {S}(\widetilde {k+4}) = \overline {{\mathfrak n}(k)-1}$
, we are done.□
$\mathsf {S}(\widetilde {k+4}) = \overline {{\mathfrak n}(k)-1}$
, we are done.□
Setting
![]() ${\sf gn}_0(A)$
to be the unique n such that
${\sf gn}_0(A)$
to be the unique n such that
![]() $A = B_n$
, we have found a monotonic self-referential Gödel numbering
$A = B_n$
, we have found a monotonic self-referential Gödel numbering
![]() ${\sf gn}_0$
, where monotonicity is defined with respect to the sub-expression relation.
${\sf gn}_0$
, where monotonicity is defined with respect to the sub-expression relation.
5 Strings
Let
![]() ${\mathcal L}$
be an arithmetical language, as introduced in Section 2.1, and let
${\mathcal L}$
be an arithmetical language, as introduced in Section 2.1, and let
![]() ${\mathcal A}$
be the alphabet of
${\mathcal A}$
be the alphabet of
![]() ${\mathcal L}$
. Let
${\mathcal L}$
. Let
![]() $\mathsf {c}$
be a fresh letter. We define:
$\mathsf {c}$
be a fresh letter. We define:
-
•
 ${\mathcal A}^{\ast }$
is the set of all strings of
${\mathcal A}^{\ast }$
is the set of all strings of
 ${\mathcal A}$
, including the empty string
${\mathcal A}$
, including the empty string
 $\varepsilon $
.
$\varepsilon $
. -
•
 ${\mathcal A}_{\sf c}$
is
${\mathcal A}_{\sf c}$
is
 ${\mathcal A}$
extended with c and
${\mathcal A}$
extended with c and
 ${\mathcal A}_{\sf c}^{\ast }$
is the set of all strings of
${\mathcal A}_{\sf c}^{\ast }$
is the set of all strings of
 ${\mathcal A}_{\sf c}$
. (In
${\mathcal A}_{\sf c}$
. (In
 ${\mathcal L}({\sf c})$
viewed as a subset of
${\mathcal L}({\sf c})$
viewed as a subset of
 ${\mathcal A}_{\sf c}^{\ast }$
, we treat c as a constant-symbol.)
${\mathcal A}_{\sf c}^{\ast }$
, we treat c as a constant-symbol.) -
•
 $\alpha \sqsubseteq \beta $
iff
$\alpha \sqsubseteq \beta $
iff
 $\alpha $
is a sub-string of
$\alpha $
is a sub-string of
 $\beta $
.
$\beta $
. -
•
 $|\alpha |$
is the length of
$|\alpha |$
is the length of
 $\alpha $
.
$\alpha $
. -
•
 ${\lfloor \alpha \rfloor }$
is the number of sub-strings-qua-type of
${\lfloor \alpha \rfloor }$
is the number of sub-strings-qua-type of
 $\alpha $
, in other words,
$\alpha $
, in other words,
 ${\lfloor \alpha \rfloor } $
is the cardinality of
${\lfloor \alpha \rfloor } $
is the cardinality of
 $\{ \beta \mid \beta \sqsubseteq \alpha \}$
.
$\{ \beta \mid \beta \sqsubseteq \alpha \}$
.
We have the following well-known fact.
Lemma 5.1. Suppose
![]() $|\alpha | = n$
. Then, the number of non-empty-sub-string-occurrences in
$|\alpha | = n$
. Then, the number of non-empty-sub-string-occurrences in
![]() $\alpha $
is
$\alpha $
is
 $\frac {n(n+1)}{2}$
. As a consequence,
$\frac {n(n+1)}{2}$
. As a consequence,
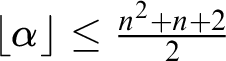 ${\lfloor \alpha \rfloor } \leq \frac {n^2+n+2}{2}$
.
${\lfloor \alpha \rfloor } \leq \frac {n^2+n+2}{2}$
.
Proof. Suppose
![]() $|\alpha | = n$
. Let us number the spaces before and after the letter-occurrences in
$|\alpha | = n$
. Let us number the spaces before and after the letter-occurrences in
![]() $\alpha $
:
$\alpha $
:
![]() $1,\dots ,n+1$
. Each non-empty-sub-string-occurrence corresponds uniquely to the pair of the space before and the space after the occurrence. So, the number of such occurrences is
$1,\dots ,n+1$
. Each non-empty-sub-string-occurrence corresponds uniquely to the pair of the space before and the space after the occurrence. So, the number of such occurrences is
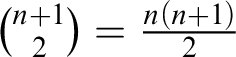 $\binom {n+1}{2} = \frac {n(n+1)}{2}$
.□
$\binom {n+1}{2} = \frac {n(n+1)}{2}$
.□
Since we are not striving for maximal efficiency, we will estimate
![]() ${\lfloor \alpha \rfloor }$
by
${\lfloor \alpha \rfloor }$
by
![]() $|\alpha |^2+1$
. Let
$|\alpha |^2+1$
. Let
![]() $\mathfrak a := {\sf S}({\sf SS}{\sf 0}\times {}$
. Then,
$\mathfrak a := {\sf S}({\sf SS}{\sf 0}\times {}$
. Then,
![]() ${\sf S}\widetilde {n} = {\sf S}\mathfrak a^n{\sf 0}{})^n$
. So,
${\sf S}\widetilde {n} = {\sf S}\mathfrak a^n{\sf 0}{})^n$
. So,
![]() $| {\sf S}\widetilde {n} | = 1+6n +1+n = 7n+2$
and, thus,
$| {\sf S}\widetilde {n} | = 1+6n +1+n = 7n+2$
and, thus,
![]() ${\lfloor {\sf S}\widetilde {n} \rfloor } \leq (7n+2)^2+1 = 49 n^2+ 28 n +5$
.
${\lfloor {\sf S}\widetilde {n} \rfloor } \leq (7n+2)^2+1 = 49 n^2+ 28 n +5$
.
Remark 5.2. We note that a much better estimate of
![]() ${\lfloor {\sf S}\widetilde {n} \rfloor }$
is possible but that its growth rate will still be quadratic. In case we switch to Polish notation, this becomes linear. Such notational choices like infix versus Polish are irrelevant in our construction and its verification when we are considering sub-expressions. In the sub-string format, they become active.
${\lfloor {\sf S}\widetilde {n} \rfloor }$
is possible but that its growth rate will still be quadratic. In case we switch to Polish notation, this becomes linear. Such notational choices like infix versus Polish are irrelevant in our construction and its verification when we are considering sub-expressions. In the sub-string format, they become active.
We provide the estimate in the Polish case. For the rest of this remark we work with Polish notation. As in Section 2.1, we write
![]() $\mathsf {M}$
for multiplication.
$\mathsf {M}$
for multiplication.
Let
![]() $\mathfrak b := {\sf SMSS}{\sf 0}$
. We have
$\mathfrak b := {\sf SMSS}{\sf 0}$
. We have
![]() ${\sf S}\widetilde {n} ={\sf S} \mathfrak b^n {\sf 0}$
. We note that, unlike
${\sf S}\widetilde {n} ={\sf S} \mathfrak b^n {\sf 0}$
. We note that, unlike
![]() $\mathfrak a$
, the string
$\mathfrak a$
, the string
![]() $\mathfrak b$
stands for a meaningful entity, to wit
$\mathfrak b$
stands for a meaningful entity, to wit
![]() $\lambda k\in \omega. 2k+1$
. See Reference Visser[34]. We count
$\lambda k\in \omega. 2k+1$
. See Reference Visser[34]. We count
![]() ${\lfloor {\sf S}\widetilde {n} \rfloor }$
as follows. Clearly
${\lfloor {\sf S}\widetilde {n} \rfloor }$
as follows. Clearly
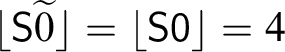 ${\lfloor {\sf S}\widetilde 0 \rfloor } = {\lfloor {\sf S} {\sf 0} \rfloor } = 4$
. Suppose
${\lfloor {\sf S}\widetilde 0 \rfloor } = {\lfloor {\sf S} {\sf 0} \rfloor } = 4$
. Suppose
![]() $n>0$
. We have:
$n>0$
. We have:
-
• The empty string: 1.
-
• The number of non-empty sub-strings of
 $\mathfrak b$
:
$\mathfrak b$
:
 $\frac {5\cdot 6}{2} -2 = 13$
. (We subtract 2, since
$\frac {5\cdot 6}{2} -2 = 13$
. (We subtract 2, since
 $\mathsf {S}$
occurs three times.)
$\mathsf {S}$
occurs three times.) -
• All strings of the form
 $\alpha \mathfrak b^i \beta $
, where
$\alpha \mathfrak b^i \beta $
, where
 $i< n-1$
,
$i< n-1$
,
 $\alpha $
is a non-empty final string of
$\alpha $
is a non-empty final string of
 $\mathfrak b$
and
$\mathfrak b$
and
 $\beta $
is a non-empty initial string of
$\beta $
is a non-empty initial string of
 $\mathfrak b$
:
$\mathfrak b$
:
 $25(n-1)$
.
$25(n-1)$
. -
• All sub-strings that contain the the final occurrence of
 ${\sf 0}$
, except
${\sf 0}$
, except
 ${\sf 0}$
itself:
${\sf 0}$
itself:
 $5n+1$
. (We note that all these strings do not occur elsewhere, since they end with
$5n+1$
. (We note that all these strings do not occur elsewhere, since they end with
 ${\sf 0} {\sf 0}$
.)
${\sf 0} {\sf 0}$
.) -
• All sub-strings that contain the initial occurrence of
 $\mathsf {S}$
, except
$\mathsf {S}$
, except
 ${\sf S}\widetilde {n}$
itself,
${\sf S}\widetilde {n}$
itself,
 $\mathsf {S}$
and
$\mathsf {S}$
and
 $\mathsf {SS}$
:
$\mathsf {SS}$
:
 $5n-1$
. (We note that the strings considered are unique since they start with
$5n-1$
. (We note that the strings considered are unique since they start with
 $\mathsf {SSM}$
. Only
$\mathsf {SSM}$
. Only
 ${\sf S}\widetilde {n}$
is an exception, since we already counted it in the previous case.)
${\sf S}\widetilde {n}$
is an exception, since we already counted it in the previous case.)
So, in toto, we have:
![]() ${\lfloor {\sf S}\widetilde {n} \rfloor } = 1+13+25(n-1)+5n+1+5n-1 = 35n-11$
. A similar estimate is also possible in the infix case, of course. However, the closing brackets will force the number to be quadratic in n.
${\lfloor {\sf S}\widetilde {n} \rfloor } = 1+13+25(n-1)+5n+1+5n-1 = 35n-11$
. A similar estimate is also possible in the infix case, of course. However, the closing brackets will force the number to be quadratic in n.
We will use the following insights.
Lemma 5.3. Suppose
![]() $m\neq 0$
and
$m\neq 0$
and
![]() $n \neq 0$
. Suppose a string
$n \neq 0$
. Suppose a string
![]() $\alpha \in {\mathcal A}^{\ast }_{\sf c}$
contains overlapping occurrences o of
$\alpha \in {\mathcal A}^{\ast }_{\sf c}$
contains overlapping occurrences o of
![]() ${\sf S}\widetilde {n}$
and p of
${\sf S}\widetilde {n}$
and p of
![]() ${\sf S} \widetilde {m}$
. Then,
${\sf S} \widetilde {m}$
. Then,
![]() $o=p$
.
$o=p$
.
Proof. Without loss of generality we may assume that p starts at the same place as or at a later place than o. Since o does not end with either
![]() $\mathsf {S}$
, or
$\mathsf {S}$
, or
![]() $\mathsf {SS}$
, the initial string
$\mathsf {SS}$
, the initial string
![]() ${\sf SS}({}$
of p must lie in o. But the only sub-string of o of the form
${\sf SS}({}$
of p must lie in o. But the only sub-string of o of the form
![]() ${\sf SS}({}$
is the intial one. Hence o and p start at the same place. By balance considerations, the matching closing brackets of the initial
${\sf SS}({}$
is the intial one. Hence o and p start at the same place. By balance considerations, the matching closing brackets of the initial
![]() ${\sf SS}({}$
in o and p should coincide. So,
${\sf SS}({}$
in o and p should coincide. So,
![]() $o=p$
□
$o=p$
□
Lemma 5.4. Suppose
![]() $\alpha \in {\mathcal A}^{\ast }_{\sf c}$
and
$\alpha \in {\mathcal A}^{\ast }_{\sf c}$
and
![]() $\beta \in {\mathcal A}^{\ast }$
, where c occurs in
$\beta \in {\mathcal A}^{\ast }$
, where c occurs in
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
is non-empty. Let
$\beta $
is non-empty. Let
![]() ${\lfloor \alpha \rfloor } = p$
,
${\lfloor \alpha \rfloor } = p$
,
![]() ${\lfloor \beta \rfloor }=q$
and
${\lfloor \beta \rfloor }=q$
and
![]() $|\beta | = r$
. Then,
$|\beta | = r$
. Then,
![]() ${\lfloor \alpha [{\sf c}:= \beta ] \rfloor } \leq (p-1)r^2+q$
. Since
${\lfloor \alpha [{\sf c}:= \beta ] \rfloor } \leq (p-1)r^2+q$
. Since
![]() $q\leq r^2+1$
, it follows that
$q\leq r^2+1$
, it follows that
![]() ${\lfloor \alpha [{\sf c}:= \beta ] \rfloor } \leq pr^2+1$
.
${\lfloor \alpha [{\sf c}:= \beta ] \rfloor } \leq pr^2+1$
.
Proof. Let
![]() $\alpha ^{\ast }$
be
$\alpha ^{\ast }$
be
![]() $\alpha [{\sf c}:= \beta ]$
where the original string
$\alpha [{\sf c}:= \beta ]$
where the original string
![]() $\alpha $
is supposed to be black and where we colored each sub-string occurrence of
$\alpha $
is supposed to be black and where we colored each sub-string occurrence of
![]() $\beta $
that resulted from the substitution with a unique color. We will consider black not to be a color here. Consider any non-empty sub-string
$\beta $
that resulted from the substitution with a unique color. We will consider black not to be a color here. Consider any non-empty sub-string
![]() $\gamma ^{\ast }$
of
$\gamma ^{\ast }$
of
![]() $\alpha ^{\ast }$
. We replace all maximal sub-string occurrences of the same color by a single occurrence of c. This corresponds to a unique sub-string occurrence of
$\alpha ^{\ast }$
. We replace all maximal sub-string occurrences of the same color by a single occurrence of c. This corresponds to a unique sub-string occurrence of
![]() $\gamma $
in
$\gamma $
in
![]() $\alpha $
. If
$\alpha $
. If
![]() $\gamma $
is c, it has
$\gamma $
is c, it has
![]() $q-1$
originals-qua-type. If
$q-1$
originals-qua-type. If
![]() $\gamma \neq {\sf c}$
, the largest number of originals-qua-type obtains when
$\gamma \neq {\sf c}$
, the largest number of originals-qua-type obtains when
![]() $\gamma $
both begins and ends with a c. This number of originals is
$\gamma $
both begins and ends with a c. This number of originals is
![]() $\leq r^2$
. So,
$\leq r^2$
. So,
![]() ${\lfloor \alpha [{\sf c} := \beta ] \rfloor } \leq (p-1)r^2 + q-1 +1 = (p-1)r^2 + q$
.□
${\lfloor \alpha [{\sf c} := \beta ] \rfloor } \leq (p-1)r^2 + q-1 +1 = (p-1)r^2 + q$
.□
Let
![]() $\alpha _0,\alpha _1,\dots $
be an effective enumeration of the strings in
$\alpha _0,\alpha _1,\dots $
be an effective enumeration of the strings in
![]() ${\mathcal A}^{\ast }_{\sf c}$
. We assume that if
${\mathcal A}^{\ast }_{\sf c}$
. We assume that if
![]() $\gamma \sqsubseteq \alpha _n$
, then, for some
$\gamma \sqsubseteq \alpha _n$
, then, for some
![]() $k\leq n$
, we have
$k\leq n$
, we have
![]() $\gamma = \alpha _k$
. The following trivial observation is very useful:
$\gamma = \alpha _k$
. The following trivial observation is very useful:
Lemma 5.5.
![]() ${\lfloor \alpha _k \rfloor } \leq k+1$
.
${\lfloor \alpha _k \rfloor } \leq k+1$
.
Here is our construction.
We construct a list
![]() $\Lambda :=(\beta _n)_{n\in \omega }$
in stages k. Let
$\Lambda :=(\beta _n)_{n\in \omega }$
in stages k. Let
![]() ${\mathfrak n}(k) := 2^{k+15}+1$
. Each stage k will result in a list
${\mathfrak n}(k) := 2^{k+15}+1$
. Each stage k will result in a list
![]() $\Lambda _k = \beta _0,\dots , \beta _{{\mathfrak n}(k)-1}$
. To simplify the presentation, we make
$\Lambda _k = \beta _0,\dots , \beta _{{\mathfrak n}(k)-1}$
. To simplify the presentation, we make
![]() $\Lambda _{-1}$
the empty list and
$\Lambda _{-1}$
the empty list and
![]() ${\mathfrak n}(-1) := 0$
.
${\mathfrak n}(-1) := 0$
.
In stage k, we act as follows. Let
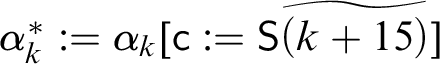 $\alpha _k^{\ast } := \alpha _k [{\sf c} := {\sf S}\widetilde {(k+15)}]$
. Let the sub-strings of
$\alpha _k^{\ast } := \alpha _k [{\sf c} := {\sf S}\widetilde {(k+15)}]$
. Let the sub-strings of
![]() $\alpha _k^{\ast }$
that do not occur in
$\alpha _k^{\ast }$
that do not occur in
![]() $\Lambda _{k-1}$
and are not of the form
$\Lambda _{k-1}$
and are not of the form
![]() $\bot ^m$
be
$\bot ^m$
be
![]() $\alpha _{i_0},\dots , \alpha _{i_{\ell -1}}$
, where the sequence
$\alpha _{i_0},\dots , \alpha _{i_{\ell -1}}$
, where the sequence
![]() $i_j$
is strictly increasing. We note that
$i_j$
is strictly increasing. We note that
![]() $\ell $
could be 0. We define
$\ell $
could be 0. We define
![]() $\beta _{{\mathfrak n}(k)-\ell +j} := \alpha _{i_j}$
, for
$\beta _{{\mathfrak n}(k)-\ell +j} := \alpha _{i_j}$
, for
![]() $j <\ell $
. Let s be the smallest number such that
$j <\ell $
. Let s be the smallest number such that
![]() $\bot ^s$
is not in
$\bot ^s$
is not in
![]() $\Lambda _{k-1}$
. We set
$\Lambda _{k-1}$
. We set
![]() $\beta _{{\mathfrak n}(k-1)+p} := \bot ^{s+p}$
, for
$\beta _{{\mathfrak n}(k-1)+p} := \bot ^{s+p}$
, for
![]() $p< {\mathfrak n}(k)-{\mathfrak n}(k-1)-\ell $
.
$p< {\mathfrak n}(k)-{\mathfrak n}(k-1)-\ell $
.
To see that our construction is well-defined it is sufficient that
![]() ${\mathfrak n}(k)-\ell \geq {\mathfrak n}(k-1)$
or, equivalently,
${\mathfrak n}(k)-\ell \geq {\mathfrak n}(k-1)$
or, equivalently,
![]() $\ell \leq {\mathfrak n}(k)-{\mathfrak n}(k-1)$
. We note that, if
$\ell \leq {\mathfrak n}(k)-{\mathfrak n}(k-1)$
. We note that, if
![]() $k=0$
, we have
$k=0$
, we have
![]() $\alpha _{0} = \varepsilon $
, and hence
$\alpha _{0} = \varepsilon $
, and hence
![]() $\ell =1$
. Moreover,
$\ell =1$
. Moreover,
![]() ${\mathfrak n}(0)-{\mathfrak n}(0-1)= 2^{15}+1$
. So, we are done. Suppose
${\mathfrak n}(0)-{\mathfrak n}(0-1)= 2^{15}+1$
. So, we are done. Suppose
![]() $k>0$
. Clearly,
$k>0$
. Clearly,
![]() ${\mathfrak n}(k)-{\mathfrak n}(k-1)= 2^{k+14}$
. In case c does not occur in
${\mathfrak n}(k)-{\mathfrak n}(k-1)= 2^{k+14}$
. In case c does not occur in
![]() $\alpha _k$
, we have
$\alpha _k$
, we have
 $\ell \leq {\lfloor \alpha _k^{\ast } \rfloor }= {\lfloor \alpha _k \rfloor } \leq k+1 \leq 2^{k+14}$
. In case c does occur
$\ell \leq {\lfloor \alpha _k^{\ast } \rfloor }= {\lfloor \alpha _k \rfloor } \leq k+1 \leq 2^{k+14}$
. In case c does occur
![]() $\alpha _k$
, we have:
$\alpha _k$
, we have:
 $$ \begin{align*} \ell \leq {\lfloor \alpha_k^{\ast} \rfloor} \leq {\lfloor \alpha_k \rfloor}|{\sf S}\widetilde {k+15}|^2 + 1 \leq (k+1)(7(k+15)+2)^2+1 \leq 2^{k+14} \end{align*} $$
$$ \begin{align*} \ell \leq {\lfloor \alpha_k^{\ast} \rfloor} \leq {\lfloor \alpha_k \rfloor}|{\sf S}\widetilde {k+15}|^2 + 1 \leq (k+1)(7(k+15)+2)^2+1 \leq 2^{k+14} \end{align*} $$
We leave the verification of the last inequality to the diligent reader.
Lemma 5.6. Suppose
![]() $\alpha _k \in {\mathcal A}^{\ast }$
. Then,
$\alpha _k \in {\mathcal A}^{\ast }$
. Then,
![]() $\alpha _k$
is in
$\alpha _k$
is in
![]() $\Lambda _k$
and, hence, in
$\Lambda _k$
and, hence, in
![]() $\Lambda $
.
$\Lambda $
.
Proof. Consider stage k. We note that
![]() $\alpha _k^{\ast } = \alpha _k$
. In case
$\alpha _k^{\ast } = \alpha _k$
. In case
![]() $\alpha _k$
occurs in
$\alpha _k$
occurs in
![]() $\Lambda _{k-1}$
, we are done. In case
$\Lambda _{k-1}$
, we are done. In case
![]() $\alpha _k$
is not in
$\alpha _k$
is not in
![]() $\Lambda _{k-1}$
and not of the form
$\Lambda _{k-1}$
and not of the form
![]() $\bot ^m$
, clearly,
$\bot ^m$
, clearly,
![]() $\alpha _k$
will be added, so we are again done. Suppose
$\alpha _k$
will be added, so we are again done. Suppose
![]() $\alpha _k = \bot ^m$
, for some m. It follows that
$\alpha _k = \bot ^m$
, for some m. It follows that
![]() $m+1={\lfloor \bot ^m \rfloor } \leq k+1$
. We note that all sub-strings of
$m+1={\lfloor \bot ^m \rfloor } \leq k+1$
. We note that all sub-strings of
![]() $\alpha _k$
are all of the form
$\alpha _k$
are all of the form
![]() $\bot ^{m'}$
, for
$\bot ^{m'}$
, for
![]() $m'\leq m$
. So
$m'\leq m$
. So
![]() $\ell = 0$
. Clearly,
$\ell = 0$
. Clearly,
![]() $m+1 \leq k+1 < {\mathfrak n}(k) - {\mathfrak n}(k-1)$
. So, all sub-expressions of
$m+1 \leq k+1 < {\mathfrak n}(k) - {\mathfrak n}(k-1)$
. So, all sub-expressions of
![]() $\alpha _k$
are either in
$\alpha _k$
are either in
![]() $\Lambda _{k-1}$
or will be added.□
$\Lambda _{k-1}$
or will be added.□
Lemma 5.7. Suppose
![]() $\gamma \sqsubseteq \beta _n$
. Then, for some
$\gamma \sqsubseteq \beta _n$
. Then, for some
![]() $j\leq n$
, we have
$j\leq n$
, we have
![]() $\gamma = \beta _j$
.
$\gamma = \beta _j$
.
Proof. Let
![]() $\gamma \sqsubseteq \beta _n$
. Suppose
$\gamma \sqsubseteq \beta _n$
. Suppose
![]() $\beta _n$
is added in stage k. Then,
$\beta _n$
is added in stage k. Then,
![]() $\beta _n$
is either of the form
$\beta _n$
is either of the form
![]() $\bot ^m$
or a sub-string of
$\bot ^m$
or a sub-string of
![]() $\alpha ^{\ast }_k$
not of the form
$\alpha ^{\ast }_k$
not of the form
![]() $\bot ^m$
.
$\bot ^m$
.
Suppose
![]() $\beta _n = \bot ^m$
. Let s be the smallest number such that
$\beta _n = \bot ^m$
. Let s be the smallest number such that
![]() $\bot ^s$
is not in
$\bot ^s$
is not in
![]() $\Lambda _{k-1}$
. For all
$\Lambda _{k-1}$
. For all
![]() $s'< s$
, we have
$s'< s$
, we have
![]() $\bot ^{s'}\in \Lambda _{k-1}$
. By our construction, all
$\bot ^{s'}\in \Lambda _{k-1}$
. By our construction, all
![]() $\bot ^{s''}$
, for
$\bot ^{s''}$
, for
![]() $s\leq s''\leq m$
are added at stage k in ascending order. So, for all
$s\leq s''\leq m$
are added at stage k in ascending order. So, for all
![]() $s^{\circ } \leq m$
, we find that
$s^{\circ } \leq m$
, we find that
![]() $\bot ^{s^{\circ }}$
precedes
$\bot ^{s^{\circ }}$
precedes
![]() $\bot ^m$
in
$\bot ^m$
in
![]() $ \Lambda _k$
. Finally,
$ \Lambda _k$
. Finally,
![]() $\gamma $
as a sub-string of
$\gamma $
as a sub-string of
![]() $\bot ^m$
is of the form
$\bot ^m$
is of the form
![]() $\bot ^{s^{\circ }}$
, for some
$\bot ^{s^{\circ }}$
, for some
![]() $s^{\circ } \leq m$
.
$s^{\circ } \leq m$
.
Suppose
![]() $\beta _n$
is added as a sub-string of
$\beta _n$
is added as a sub-string of
![]() $\alpha ^{\ast }_k$
not of the form
$\alpha ^{\ast }_k$
not of the form
![]() $\bot ^m$
. First suppose
$\bot ^m$
. First suppose
![]() $\gamma = \bot ^p$
. We note that
$\gamma = \bot ^p$
. We note that
![]() $p+1 = {\lfloor \bot ^p \rfloor } < {\lfloor \alpha _k \rfloor } \leq k+1$
. This tells us, by Lemma 5.6, that
$p+1 = {\lfloor \bot ^p \rfloor } < {\lfloor \alpha _k \rfloor } \leq k+1$
. This tells us, by Lemma 5.6, that
![]() $\bot ^p$
is in
$\bot ^p$
is in
![]() $\Lambda _{k-1}$
. Hence, it is added to
$\Lambda _{k-1}$
. Hence, it is added to
![]() $\Lambda $
before
$\Lambda $
before
![]() $\beta _n$
. Now suppose that
$\beta _n$
. Now suppose that
![]() $\gamma $
is not of the form
$\gamma $
is not of the form
![]() $\bot ^p$
. Then, either
$\bot ^p$
. Then, either
![]() $\gamma $
is in
$\gamma $
is in
![]() $\Lambda _{k-1}$
or added to
$\Lambda _{k-1}$
or added to
![]() $\Lambda _k$
before
$\Lambda _k$
before
![]() $\beta _n$
.□
$\beta _n$
.□
Lemma 5.8. The enumeration
![]() $\Lambda $
is without repetitions.
$\Lambda $
is without repetitions.
Proof. Consider any
![]() $\gamma \in {\mathcal A}^{\ast }$
. If
$\gamma \in {\mathcal A}^{\ast }$
. If
![]() $\gamma $
is not of the form
$\gamma $
is not of the form
![]() $\bot ^m$
by our construction it will be only added once. Suppose
$\bot ^m$
by our construction it will be only added once. Suppose
![]() $ \gamma = \bot ^m$
. We note that, by Lemma 5.7, the n such that
$ \gamma = \bot ^m$
. We note that, by Lemma 5.7, the n such that
![]() $\bot ^n \in \Lambda _{k-1}$
are downwards closed. This means that, in our construction, there is no
$\bot ^n \in \Lambda _{k-1}$
are downwards closed. This means that, in our construction, there is no
![]() $m\geq s$
, such that
$m\geq s$
, such that
![]() $\bot ^m \in \Lambda _{k-1}$
. So all the
$\bot ^m \in \Lambda _{k-1}$
. So all the
![]() $\bot ^m$
that are added in any stage k are new.□
$\bot ^m$
that are added in any stage k are new.□
Lemma 5.9. Suppose
![]() ${\sf S}\widetilde {n}$
occurs in
${\sf S}\widetilde {n}$
occurs in
![]() $\Lambda _k$
, then
$\Lambda _k$
, then
![]() $n \leq k+15$
.
$n \leq k+15$
.
Proof. We prove this by induction on k. In stage 0, we easily verify that the largest term of the form
![]() $\mathsf {S}\widetilde {n}$
can be at most
$\mathsf {S}\widetilde {n}$
can be at most
![]() $\mathsf {S} \widetilde {15}$
.
$\mathsf {S} \widetilde {15}$
.
Suppose, we have our desired estimate for
![]() $k-1$
, where
$k-1$
, where
![]() $k>0$
. We prove our estimate for k. Clearly, the
$k>0$
. We prove our estimate for k. Clearly, the
![]() $\mathsf {S}\widetilde {n}$
occurring in
$\mathsf {S}\widetilde {n}$
occurring in
![]() $\Lambda _{k-1}$
do satisfy our estimate. Moreover, all the
$\Lambda _{k-1}$
do satisfy our estimate. Moreover, all the
![]() $\bot ^p$
added in stage k do not provide new elements of the form
$\bot ^p$
added in stage k do not provide new elements of the form
![]() $\mathsf {S}\widetilde {n}$
. So, the only interesting case is the case where
$\mathsf {S}\widetilde {n}$
. So, the only interesting case is the case where
![]() $\alpha _k$
is not a string of
$\alpha _k$
is not a string of
![]() $\bot $
’s. Suppose it is not. The
$\bot $
’s. Suppose it is not. The
![]() ${\sf S}\widetilde {n}$
that are added are all sub-strings of
${\sf S}\widetilde {n}$
that are added are all sub-strings of
 $ \alpha ^{\ast }_k= \alpha _k[{\sf c} := {\sf S}\widetilde {(k+15)}]$
. So, we should focus on the largest such sub-string. Suppose
$ \alpha ^{\ast }_k= \alpha _k[{\sf c} := {\sf S}\widetilde {(k+15)}]$
. So, we should focus on the largest such sub-string. Suppose
![]() ${\sf S}\widetilde {n} \sqsubseteq \alpha ^{\ast }_k$
. There are two possibilities:
${\sf S}\widetilde {n} \sqsubseteq \alpha ^{\ast }_k$
. There are two possibilities:
-
i.
 ${\sf S}\widetilde {n}\sqsubseteq \alpha _k$
. In this case, we have
${\sf S}\widetilde {n}\sqsubseteq \alpha _k$
. In this case, we have
 $n < {\lfloor \mathsf {S}\widetilde {n} \rfloor } \leq {\lfloor \alpha _k \rfloor } \leq k+1 \leq k +15$
.
$n < {\lfloor \mathsf {S}\widetilde {n} \rfloor } \leq {\lfloor \alpha _k \rfloor } \leq k+1 \leq k +15$
. -
ii.
 $n= k+15$
, since the sub-string results from the substitution for c.
$n= k+15$
, since the sub-string results from the substitution for c.
In each of the possible cases, we are done.□
Lemma 5.10. Consider any
![]() $\alpha $
such that c occurs in
$\alpha $
such that c occurs in
![]() $\beta $
. Then, for some n,
$\beta $
. Then, for some n,
![]() $\beta _n = \alpha [{\sf c}:= \overline {n}]$
.
$\beta _n = \alpha [{\sf c}:= \overline {n}]$
.
Proof. Suppose c occurs in
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\alpha := \alpha _k$
. The only thing we have to show is that
$\alpha := \alpha _k$
. The only thing we have to show is that
![]() $\alpha ^{\ast }_k$
is not in
$\alpha ^{\ast }_k$
is not in
![]() $\Lambda _{k-1}$
. This is certainly true for
$\Lambda _{k-1}$
. This is certainly true for
![]() $k=0$
. Suppose
$k=0$
. Suppose
![]() $k>0$
. We note that
$k>0$
. We note that
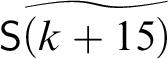 ${\sf S}\widetilde {(k+15)}$
occurs in
${\sf S}\widetilde {(k+15)}$
occurs in
![]() $\alpha ^{\ast }_k$
. So, it is sufficient to show that
$\alpha ^{\ast }_k$
. So, it is sufficient to show that
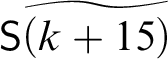 ${\sf S}\widetilde {(k+15)}$
does not occur in
${\sf S}\widetilde {(k+15)}$
does not occur in
![]() $\Lambda _{k-1}$
. By Lemma 5.9, whenever
$\Lambda _{k-1}$
. By Lemma 5.9, whenever
![]() $\mathsf {S}\widetilde {n}$
occurs in
$\mathsf {S}\widetilde {n}$
occurs in
![]() $\Lambda _{k-1}$
, we have
$\Lambda _{k-1}$
, we have
![]() $n \leq k+14$
. We may conclude that
$n \leq k+14$
. We may conclude that
 $\beta _{{\mathfrak n}(k)-1} = \alpha _k[\mathsf {c} := \mathsf {S}(\widetilde {k+15})]$
. Since
$\beta _{{\mathfrak n}(k)-1} = \alpha _k[\mathsf {c} := \mathsf {S}(\widetilde {k+15})]$
. Since
 $\mathsf {S}(\widetilde {k+15}) = \overline {{\mathfrak n}(k)-1}$
, we are done.□
$\mathsf {S}(\widetilde {k+15}) = \overline {{\mathfrak n}(k)-1}$
, we are done.□
Setting
![]() ${\sf gn}_1(\alpha )$
to be the unique n such that
${\sf gn}_1(\alpha )$
to be the unique n such that
![]() $\alpha = \beta _n$
, we have found a monotonic self-referential Gödel numbering
$\alpha = \beta _n$
, we have found a monotonic self-referential Gödel numbering
![]() ${\sf gn}_1$
. Here monotonicity is defined with respect to the sub-string relation.
${\sf gn}_1$
. Here monotonicity is defined with respect to the sub-string relation.
6 Gödel Numerals as Quotations
In the philosophical literature, Gödel numerals are typically conceived of as canonical names for their coded expressions. One of the most canonical naming devices is quotation, assigning to each expression A its name “
![]() $A.$
” Accordingly, the Tarski biconditional
$A.$
” Accordingly, the Tarski biconditional
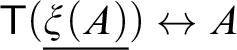 $\mathsf {T}(\underline {\xi (A)}) \leftrightarrow A$
for instance is often taken as an arithmetical proxy for the sentence “‘A’ is true iff
$\mathsf {T}(\underline {\xi (A)}) \leftrightarrow A$
for instance is often taken as an arithmetical proxy for the sentence “‘A’ is true iff
![]() $A.$
”
$A.$
”
The standard numeral
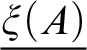 $\underline {\xi (A)}$
is prima facie not the only candidate for an arithmetical proxy for quotation. As there are different adequate ways to quote an expression A, such as “A”, ‘A’,
$\underline {\xi (A)}$
is prima facie not the only candidate for an arithmetical proxy for quotation. As there are different adequate ways to quote an expression A, such as “A”, ‘A’,
![]() , etc., different numerals may be reasonably taken as adequate arithmetical proxies of A’s quotation, such as
, etc., different numerals may be reasonably taken as adequate arithmetical proxies of A’s quotation, such as
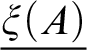 $\underline {\xi (A)}$
,
$\underline {\xi (A)}$
,
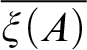 $\overline {\xi (A)}$
, etc.Footnote
11
$\overline {\xi (A)}$
, etc.Footnote
11
Once
![]() $\nu $
-numerals are taken as adequate arithmetical proxies for quotations, another criterion for numberings may be extracted from the basic idea underlying monotonicity, which has been suggested by Halbach Reference Halbach[9]. Recall that monotonic numberings have the property that the code of an expression A is larger than the code of any expression (strictly) contained in A. Since each quotation properly contains its quoted expression, it may be argued, along the lines of Section 3.1, that adequate numberings should preserve this structural feature by requiring that the code of the Gödel
$\nu $
-numerals are taken as adequate arithmetical proxies for quotations, another criterion for numberings may be extracted from the basic idea underlying monotonicity, which has been suggested by Halbach Reference Halbach[9]. Recall that monotonic numberings have the property that the code of an expression A is larger than the code of any expression (strictly) contained in A. Since each quotation properly contains its quoted expression, it may be argued, along the lines of Section 3.1, that adequate numberings should preserve this structural feature by requiring that the code of the Gödel
![]() $\nu $
-numeral of an expression A is larger than the code of A itself:
$\nu $
-numeral of an expression A is larger than the code of A itself:
-
M4
 $(\nu )$
.
$(\nu )$
.
 $\ \xi (A) < \xi ( \nu (\xi (A)) )$
for all
$\ \xi (A) < \xi ( \nu (\xi (A)) )$
for all
 $A \in \mathcal {L}$
,
$A \in \mathcal {L}$
,
We call a numbering
![]() $\xi $
of
$\xi $
of
![]() $\mathcal {L}$
strongly monotonic for
$\mathcal {L}$
strongly monotonic for
![]() $\nu $
-numerals, if
$\nu $
-numerals, if
![]() $\xi $
satisfies M1–M3 as well as M4(
$\xi $
satisfies M1–M3 as well as M4(
![]() $\nu $
).
$\nu $
).
We note that M4(
![]() $\nu $
) rules out that
$\nu $
) rules out that
![]() $\xi ({\sf 0}) = 0$
and
$\xi ({\sf 0}) = 0$
and
![]() $\nu (0) = {\sf 0}$
, which holds for certain length-first orderings and standard numerals. These standard numberings are not excluded by its weakened version M4
$\nu (0) = {\sf 0}$
, which holds for certain length-first orderings and standard numerals. These standard numberings are not excluded by its weakened version M4
![]() $^{\ast }$
(
$^{\ast }$
(
![]() $\nu $
), which is obtained by replacing
$\nu $
), which is obtained by replacing
![]() $<$
by
$<$
by
![]() $\leq $
in M4(
$\leq $
in M4(
![]() $\nu $
). In what follows, we will always employ the version of M4(
$\nu $
). In what follows, we will always employ the version of M4(
![]() $\nu $
) which yields the stronger result.
$\nu $
) which yields the stronger result.
Since the standard numeral
![]() $\underline {n}$
has n-many proper subterms, any numbering satisfying M1 also satisfies M4(
$\underline {n}$
has n-many proper subterms, any numbering satisfying M1 also satisfies M4(
![]() $\underline {\cdot }$
). Strong monotonicity is however not entailed by monotonicity when efficient numerals are employed. For instance, as will follow from the next lemma, the numbering
$\underline {\cdot }$
). Strong monotonicity is however not entailed by monotonicity when efficient numerals are employed. For instance, as will follow from the next lemma, the numbering
![]() ${\sf gn}_0$
is monotonic but not strongly monotonic for efficient numerals. In fact, strong monotonicity is incompatible with the self-referentiality of numberings.
${\sf gn}_0$
is monotonic but not strongly monotonic for efficient numerals. In fact, strong monotonicity is incompatible with the self-referentiality of numberings.
Lemma 6.1. Let
![]() $\nu $
be a numeral function for
$\nu $
be a numeral function for
![]() $\mathcal {L}$
. There is no numbering of
$\mathcal {L}$
. There is no numbering of
![]() $\mathcal {L}$
which is self-referential for
$\mathcal {L}$
which is self-referential for
![]() $\nu $
and satisfies M3 and M4
$\nu $
and satisfies M3 and M4
![]() $^{\ast }$
(
$^{\ast }$
(
![]() $\nu $
).
$\nu $
).
Proof. Suppose
![]() $\xi $
is a self-referential numbering of
$\xi $
is a self-referential numbering of
![]() $\mathcal {L}$
. Consider any formula
$\mathcal {L}$
. Consider any formula
![]() $A(x)$
with free variable x and
$A(x)$
with free variable x and
![]() $n \in \omega $
such that
$n \in \omega $
such that
![]() $\xi (A(\nu (n))) = n$
. Since
$\xi (A(\nu (n))) = n$
. Since
![]() $\nu (n) \prec A(\nu (n))$
, using M3 and M4
$\nu (n) \prec A(\nu (n))$
, using M3 and M4
![]() $^{\ast }$
(
$^{\ast }$
(
![]() $\nu $
) yields the contradiction
$\nu $
) yields the contradiction
□
Thus, if we strengthen the conception of monotonicity in the above manner, then, by Halbach’s standards, there are no reasonable numberings which are self-referential.
6.1 A critical remark
We are somewhat sceptical whether strong monotonicity really is a necessary constraint for reasonable numberings (see also footnote 11). For instance, we now show that the length-first numbering is not strongly monotonic for a fairly reasonable numeral function based on prime decomposition. Any philosophically stable view which excludes self-referential numberings as adequate formalisation choices along the above lines, hence appears to be committed to render the introduced numeral function below an inadequate naming device.
Example 6.2. Let
![]() $\mathcal {L}^{\sf Q} := \mathcal {L}^0 \cup \{ {\sf Q} \}$
, where
$\mathcal {L}^{\sf Q} := \mathcal {L}^0 \cup \{ {\sf Q} \}$
, where
![]() ${\sf Q}$
is a unary function symbol for taking the square. Let
${\sf Q}$
is a unary function symbol for taking the square. Let
![]() ${\mathfrak g}$
be a numbering of
${\mathfrak g}$
be a numbering of
![]() $\mathcal {L}^{\sf Q}$
based on the length-first ordering.
$\mathcal {L}^{\sf Q}$
based on the length-first ordering.
Are there plausible numerals for which strong monotonicity fails w.r.t.
![]() ${\mathfrak g}$
? This is indeed the case. We give an example of such numerals that seems reasonably natural.
${\mathfrak g}$
? This is indeed the case. We give an example of such numerals that seems reasonably natural.
We consider the following numeral function
![]() $\mathsf {pd}$
. (‘
$\mathsf {pd}$
. (‘
![]() $\mathsf {pd}$
’ stands for prime decomposition.)
$\mathsf {pd}$
’ stands for prime decomposition.)
-
i.
 ${\sf pd}(0) := {\sf 0}$
and
${\sf pd}(0) := {\sf 0}$
and
 ${\sf pd}(1) := {\sf S}{\sf 0}$
.
${\sf pd}(1) := {\sf S}{\sf 0}$
. -
ii. Suppose
 $n> 1$
, and n is not a power of a prime. Let p be the smallest prime that divides n. Say
$n> 1$
, and n is not a power of a prime. Let p be the smallest prime that divides n. Say
 $n = p^i\cdot m$
, where p does not divide m and
$n = p^i\cdot m$
, where p does not divide m and
 $i>0$
. Then,
$i>0$
. Then,
 ${\sf pd}(n) := \times {\sf pd}(p^i){\sf pd}(m)$
.
${\sf pd}(n) := \times {\sf pd}(p^i){\sf pd}(m)$
. -
iii. Suppose
 $n = p^i$
, where p is prime and
$n = p^i$
, where p is prime and
 $i>0$
. We take
$i>0$
. We take
 ${\sf pd}(p) := \underline p$
. In case
${\sf pd}(p) := \underline p$
. In case
 $i = 2k$
, for
$i = 2k$
, for
 $k>0$
, we set
$k>0$
, we set
 ${\sf pd}(n) := {\sf Q}\,{\sf pd}(p^k)$
. In case
${\sf pd}(n) := {\sf Q}\,{\sf pd}(p^k)$
. In case
 $i = 2k+1$
, for
$i = 2k+1$
, for
 $k>0$
, we set
$k>0$
, we set
 ${\sf pd}(n) := \times \underline p\, {\sf Q}\,{\sf pd}(p^k)$
.
${\sf pd}(n) := \times \underline p\, {\sf Q}\,{\sf pd}(p^k)$
.
We find that, e.g.,
 $$ \begin{align*} {\sf pd}(2^{2^m}) = \overbrace{{\sf Q} \cdots {\sf Q}}^{m \times}\underline 2. \end{align*} $$
$$ \begin{align*} {\sf pd}(2^{2^m}) = \overbrace{{\sf Q} \cdots {\sf Q}}^{m \times}\underline 2. \end{align*} $$
It follows that
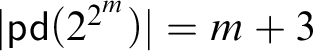 $|{\sf pd}(2^{2^m})| = m + 3$
. Hence, by Lemma 2.3,
$|{\sf pd}(2^{2^m})| = m + 3$
. Hence, by Lemma 2.3,
 $$ \begin{align*} {\mathfrak g}({\sf pd}(2^{2^m})) \leq \frac{16^{m+4}-1}{15}. \end{align*} $$
$$ \begin{align*} {\mathfrak g}({\sf pd}(2^{2^m})) \leq \frac{16^{m+4}-1}{15}. \end{align*} $$
Since
![]() $2^{2^m}$
has double exponential growth, the failure of strong monotonicity is immediate.
$2^{2^m}$
has double exponential growth, the failure of strong monotonicity is immediate.
We note that
![]() ${\sf pd}$
has good properties for multiplication but does not seem to be very friendly towards successor and addition.
${\sf pd}$
has good properties for multiplication but does not seem to be very friendly towards successor and addition.
One can imagine many variants of
![]() ${\sf pd}$
. For example, we can replace
${\sf pd}$
. For example, we can replace
![]() $\underline p$
by
$\underline p$
by
![]() $\overline p$
in the definition. Alternatively, we can make
$\overline p$
in the definition. Alternatively, we can make
![]() $\mathfrak {p}$
where we replace clause (iii) by:
$\mathfrak {p}$
where we replace clause (iii) by:
-
• Suppose
 $n = p^i$
, where p is prime and
$n = p^i$
, where p is prime and
 $i>0$
. We take
$i>0$
. We take
 ${\mathfrak p}(p) := {\sf S}{\mathfrak p}(p-1)$
. In case
${\mathfrak p}(p) := {\sf S}{\mathfrak p}(p-1)$
. In case
 $i = 2k$
, for
$i = 2k$
, for
 $k>0$
, we set
$k>0$
, we set
 $\mathfrak p(n) := {\sf Q}\,\mathfrak p(p^k)$
. In case
$\mathfrak p(n) := {\sf Q}\,\mathfrak p(p^k)$
. In case
 $i = 2k+1$
, for
$i = 2k+1$
, for
 $k>0$
, we set
$k>0$
, we set
 $\mathfrak p(n) := \times {\sf S}\mathfrak p(p-1)\,{\sf Q}\,\mathfrak p(p^k)$
.
$\mathfrak p(n) := \times {\sf S}\mathfrak p(p-1)\,{\sf Q}\,\mathfrak p(p^k)$
.
We leave an in-depth discussion of this constraint’s adequacy for another occasion and, from now on, simply assume that there are good reasons to consider strong monotonicity to be a necessary constraint for reasonable numberings. In the next section we further examine the implications of this constraint on the attainability of self-reference.
6.2 A strongly monotonic numbering with strong diagonalisation
While strong monotonicity excludes self-referential numberings (Lemma 6.1), we now show that this constraint is not sufficiently restrictive to rule out m-self-reference in
![]() $\mathcal {L}^0$
. In particular, we construct a strongly monotonic numbering
$\mathcal {L}^0$
. In particular, we construct a strongly monotonic numbering
![]() ${\sf gn}_2$
for efficient numerals which satisfies the Strong Diagonal Lemma for
${\sf gn}_2$
for efficient numerals which satisfies the Strong Diagonal Lemma for
![]() $\mathcal {L} \supseteq \mathcal {L}^0$
:
$\mathcal {L} \supseteq \mathcal {L}^0$
:
Lemma 6.3 (Strong Diagonal Lemma for
 ${\mathcal {L}}$
)
${\mathcal {L}}$
)
Let C be an
![]() $\mathcal {L}$
-expression with x as a free variable. Then there exists a closed term t in
$\mathcal {L}$
-expression with x as a free variable. Then there exists a closed term t in
![]() $\mathcal {L}$
such that
$\mathcal {L}$
such that
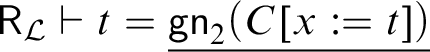 ${\mathsf {R}_{\mathcal {L}} \vdash t = \underline {{\sf gn}_2(C[x := t])}}$
.
${\mathsf {R}_{\mathcal {L}} \vdash t = \underline {{\sf gn}_2(C[x := t])}}$
.
We note that we escape Lemma 6.1 here by allowing t to be different from the efficient numeral of the value of t.
Let
![]() ${\mathcal L}$
be an arithmetical language, as introduced in Section 2.1, and let
${\mathcal L}$
be an arithmetical language, as introduced in Section 2.1, and let
![]() ${\mathcal L}(\mathsf {c})$
be
${\mathcal L}(\mathsf {c})$
be
![]() ${\mathcal L}$
extended with a fresh constant
${\mathcal L}$
extended with a fresh constant
![]() $\mathsf {c}$
. Let
$\mathsf {c}$
. Let
![]() $A_0,A_1,\dots $
be an effective enumeration of all expressions of
$A_0,A_1,\dots $
be an effective enumeration of all expressions of
![]() ${\mathcal L}(\mathsf {c})$
. We assume that if
${\mathcal L}(\mathsf {c})$
. We assume that if
![]() $C \preceq A_n$
, then, for some
$C \preceq A_n$
, then, for some
![]() $k\leq n$
, we have
$k\leq n$
, we have
![]() $C=A_k$
.
$C=A_k$
.
We define
![]() ${\lceil A \rceil }$
as the number of subexpressions-qua-type of A, in other words,
${\lceil A \rceil }$
as the number of subexpressions-qua-type of A, in other words,
![]() ${\lceil A \rceil } $
is the cardinality of
${\lceil A \rceil } $
is the cardinality of
![]() $\{ B\mid B\preceq A \}$
. The following trivial observation is very useful:
$\{ B\mid B\preceq A \}$
. The following trivial observation is very useful:
Lemma 6.4.
![]() ${\lceil A_k \rceil } \leq k+1$
.
${\lceil A_k \rceil } \leq k+1$
.
Let the function
![]() $\widehat {\cdot } \colon \omega \to \mathcal {L}$
be given by setting
$\widehat {\cdot } \colon \omega \to \mathcal {L}$
be given by setting
![]() $\widehat {0} := \mathsf {v}$
and
$\widehat {0} := \mathsf {v}$
and
 $\widehat {n+1} := \widehat {n} '$
. As in the case of standard numerals, expressions of the form
$\widehat {n+1} := \widehat {n} '$
. As in the case of standard numerals, expressions of the form
![]() $\widehat m$
are downwards closed with regard to the sub-expression relation and we have that
$\widehat m$
are downwards closed with regard to the sub-expression relation and we have that
![]() ${\lceil \widehat m \rceil } = m+1$
. In the following construction, we use expressions of the form
${\lceil \widehat m \rceil } = m+1$
. In the following construction, we use expressions of the form
![]() $\widehat m$
instead of standard numerals as fillers. This ensures that the constructed enumeration does not start with
$\widehat m$
instead of standard numerals as fillers. This ensures that the constructed enumeration does not start with
![]() $\overline 0$
and thus that the resulting numbering is strongly monotonic.
$\overline 0$
and thus that the resulting numbering is strongly monotonic.
Here is our construction.
We construct a list
![]() $\Lambda :=(B_n)_{n\in \omega }$
in stages k. Let
$\Lambda :=(B_n)_{n\in \omega }$
in stages k. Let
![]() ${\mathfrak n}(k) := 2^{2k+4}+1$
. Each stage k will result in a list
${\mathfrak n}(k) := 2^{2k+4}+1$
. Each stage k will result in a list
![]() $\Lambda _k = B_0,\dots , B_{{\mathfrak n}(k)-1}$
. To simplify the presentation, we make
$\Lambda _k = B_0,\dots , B_{{\mathfrak n}(k)-1}$
. To simplify the presentation, we make
![]() $\Lambda _{-1}$
the empty list and
$\Lambda _{-1}$
the empty list and
![]() ${\mathfrak n}(-1) := 0$
.
${\mathfrak n}(-1) := 0$
.
In stage k, we act as follows. Let
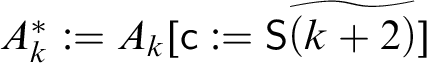 $A_k^{\ast } := A_k [{\sf c} := {\sf S}\widetilde {(k+2)}]$
. Let the sub-expressions of
$A_k^{\ast } := A_k [{\sf c} := {\sf S}\widetilde {(k+2)}]$
. Let the sub-expressions of
![]() $A_k^{\ast }$
that do not occur in
$A_k^{\ast }$
that do not occur in
![]() $\Lambda _{k-1}$
and are not of the form
$\Lambda _{k-1}$
and are not of the form
![]() $\widehat m$
be
$\widehat m$
be
![]() $A_{i_0},\dots , A_{i_{\ell -1}}$
, where the sequence
$A_{i_0},\dots , A_{i_{\ell -1}}$
, where the sequence
![]() $i_j$
is strictly increasing. We note that
$i_j$
is strictly increasing. We note that
![]() $\ell $
could be 0. We define
$\ell $
could be 0. We define
![]() $B_{{\mathfrak n}(k)-\ell +j} := A_{i_j}$
, for
$B_{{\mathfrak n}(k)-\ell +j} := A_{i_j}$
, for
![]() $j <\ell $
. Let s be the smallest number such that
$j <\ell $
. Let s be the smallest number such that
![]() $\widehat s$
is not in
$\widehat s$
is not in
![]() $\Lambda _{k-1}$
. We set
$\Lambda _{k-1}$
. We set
 $B_{{\mathfrak n}(k-1)+p} := \widehat {s+p}$
, for
$B_{{\mathfrak n}(k-1)+p} := \widehat {s+p}$
, for
![]() $p< {\mathfrak n}(k)-{\mathfrak n}(k-1)-\ell $
.
$p< {\mathfrak n}(k)-{\mathfrak n}(k-1)-\ell $
.
To see that our construction is well-defined it is sufficient that
![]() ${\mathfrak n}(k)-\ell \geq {\mathfrak n}(k-1)$
or, equivalently,
${\mathfrak n}(k)-\ell \geq {\mathfrak n}(k-1)$
or, equivalently,
![]() $\ell \leq {\mathfrak n}(k)-{\mathfrak n}(k-1)$
. We note that:
$\ell \leq {\mathfrak n}(k)-{\mathfrak n}(k-1)$
. We note that:
 $$ \begin{align} \ell \leq {\lceil A_k^{\ast} \rceil} \leq {\lceil A_k \rceil}+{\lceil {\sf S}\widetilde {(k+2)} \rceil}-1 \leq k +1 + 2(k+2)+3 = 3 k + 8. \end{align} $$
$$ \begin{align} \ell \leq {\lceil A_k^{\ast} \rceil} \leq {\lceil A_k \rceil}+{\lceil {\sf S}\widetilde {(k+2)} \rceil}-1 \leq k +1 + 2(k+2)+3 = 3 k + 8. \end{align} $$
(The
![]() $-1$
in the right-hand-side of the second inequality can be seen as follows. In case c occurs in
$-1$
in the right-hand-side of the second inequality can be seen as follows. In case c occurs in
![]() $A_k$
it is subtracted in the substitution. If c does not occur, we have
$A_k$
it is subtracted in the substitution. If c does not occur, we have
![]() $A_k = A_k^{\ast }$
and, from this, the inequality follows immediately.)
$A_k = A_k^{\ast }$
and, from this, the inequality follows immediately.)
If
![]() $k=0$
, we have
$k=0$
, we have
![]() $3\cdot 0 +8 = 8 < 17 = 2^{2(0+2)}+1-0 = {\mathfrak n}(0) - {\mathfrak n}(-1)$
. Let
$3\cdot 0 +8 = 8 < 17 = 2^{2(0+2)}+1-0 = {\mathfrak n}(0) - {\mathfrak n}(-1)$
. Let
![]() $k>0$
. We find:
$k>0$
. We find:
Lemma 6.5. Suppose
![]() $A_k \in {\mathcal L}$
. Then,
$A_k \in {\mathcal L}$
. Then,
![]() $A_k$
is in
$A_k$
is in
![]() $\Lambda _k$
and, hence, in
$\Lambda _k$
and, hence, in
![]() $\Lambda $
.
$\Lambda $
.
Proof. Consider stage k. We note that
![]() $A_k^{\ast } = A_k$
. In case
$A_k^{\ast } = A_k$
. In case
![]() $A_k$
occurs in
$A_k$
occurs in
![]() $\Lambda _{k-1}$
, we are done. In case
$\Lambda _{k-1}$
, we are done. In case
![]() $A_k$
is not in
$A_k$
is not in
![]() $\Lambda _{k-1}$
and not of the form
$\Lambda _{k-1}$
and not of the form
![]() $\widehat m$
, clearly,
$\widehat m$
, clearly,
![]() $A_k$
will be added, so we are again done. Suppose
$A_k$
will be added, so we are again done. Suppose
![]() $A_k = \widehat m$
, for some m. It follows that
$A_k = \widehat m$
, for some m. It follows that
![]() $m+1={\lceil \widehat m \rceil } \leq k+1$
. We note that all sub-expressions of
$m+1={\lceil \widehat m \rceil } \leq k+1$
. We note that all sub-expressions of
![]() $A_k$
are of the form
$A_k$
are of the form
![]() $\widehat {n}$
, for
$\widehat {n}$
, for
![]() $n\leq m$
. So
$n\leq m$
. So
![]() $\ell = 0$
. Clearly,
$\ell = 0$
. Clearly,
![]() $m+1 \leq k+1 < {\mathfrak n}(k) - {\mathfrak n}(k-1)$
. So, all sub-expressions of
$m+1 \leq k+1 < {\mathfrak n}(k) - {\mathfrak n}(k-1)$
. So, all sub-expressions of
![]() $A_k$
are either in
$A_k$
are either in
![]() $\Lambda _{k-1}$
or will be added.□
$\Lambda _{k-1}$
or will be added.□
Lemma 6.6. Suppose
![]() $C \preceq B_n$
. Then, for some
$C \preceq B_n$
. Then, for some
![]() $j\leq n$
, we have
$j\leq n$
, we have
![]() $C = B_j$
.
$C = B_j$
.
Proof. Let
![]() $C \preceq B_n$
. Suppose
$C \preceq B_n$
. Suppose
![]() $B_n$
is added in stage k. Then,
$B_n$
is added in stage k. Then,
![]() $B_{n}$
is either of the form
$B_{n}$
is either of the form
![]() $\widehat m$
or a sub-expression of
$\widehat m$
or a sub-expression of
![]() $A^{\ast }_k$
not of the form
$A^{\ast }_k$
not of the form
![]() $\widehat m$
.
$\widehat m$
.
Suppose
![]() $B_n = \widehat m$
. Let s be the smallest number such that
$B_n = \widehat m$
. Let s be the smallest number such that
![]() $\widehat s$
is not in
$\widehat s$
is not in
![]() $\Lambda _{k-1}$
. For all
$\Lambda _{k-1}$
. For all
![]() $u< s$
, we have
$u< s$
, we have
![]() $\widehat u\in \Lambda _{k-1}$
. By our construction, all
$\widehat u\in \Lambda _{k-1}$
. By our construction, all
![]() $\widehat v$
, for
$\widehat v$
, for
![]() $s\leq v \leq m$
are added at stage k in ascending order. So, for all
$s\leq v \leq m$
are added at stage k in ascending order. So, for all
![]() $w \leq m$
, we find that
$w \leq m$
, we find that
![]() $\widehat w$
precedes
$\widehat w$
precedes
![]() $\widehat m$
in
$\widehat m$
in
![]() $ \Lambda _k$
. Finally, each sub-expression C of
$ \Lambda _k$
. Finally, each sub-expression C of
![]() $\widehat m$
is of the form
$\widehat m$
is of the form
![]() $\widehat w$
, for some
$\widehat w$
, for some
![]() $w \leq m$
.
$w \leq m$
.
Suppose
![]() $B_n$
is added as a sub-expression of
$B_n$
is added as a sub-expression of
![]() $A^{\ast }_k$
not of the form
$A^{\ast }_k$
not of the form
![]() $\widehat m$
. First suppose
$\widehat m$
. First suppose
![]() $C= \widehat p$
. We note that
$C= \widehat p$
. We note that
![]() $p+1 = {\lceil \widehat p \rceil } < {\lceil A_k \rceil } \leq k+1$
. This tells us, by Lemma 6.5, that
$p+1 = {\lceil \widehat p \rceil } < {\lceil A_k \rceil } \leq k+1$
. This tells us, by Lemma 6.5, that
![]() $\widehat p$
is in
$\widehat p$
is in
![]() $\Lambda _{k-1}$
. Hence, it is added to
$\Lambda _{k-1}$
. Hence, it is added to
![]() $\Lambda $
before
$\Lambda $
before
![]() $B_n$
. Now suppose that C is not of the form
$B_n$
. Now suppose that C is not of the form
![]() $\widehat p$
. Then, either C is in
$\widehat p$
. Then, either C is in
![]() $\Lambda _{k-1}$
or added to
$\Lambda _{k-1}$
or added to
![]() $\Lambda _k$
before
$\Lambda _k$
before
![]() $B_n$
.□
$B_n$
.□
Lemma 6.7. The enumeration
![]() $\Lambda $
is without repetitions.
$\Lambda $
is without repetitions.
Proof. Consider any
![]() $C \in {\mathcal L}$
. If C is not of the form
$C \in {\mathcal L}$
. If C is not of the form
![]() $\widehat m$
by our construction it will be only added once.
$\widehat m$
by our construction it will be only added once.
Suppose
![]() $ C = \widehat m$
. We note that, by Lemma 6.6, the n such that
$ C = \widehat m$
. We note that, by Lemma 6.6, the n such that
![]() $\widehat n \in \Lambda _{k-1}$
are downwards closed. This means that, in our construction, there is no
$\widehat n \in \Lambda _{k-1}$
are downwards closed. This means that, in our construction, there is no
![]() $m\geq s$
, such that
$m\geq s$
, such that
![]() $\widehat m \in \Lambda _{k-1}$
. So all the
$\widehat m \in \Lambda _{k-1}$
. So all the
![]() $\widehat m$
that are added in any stage k are new.□
$\widehat m$
that are added in any stage k are new.□
Lemma 6.8. Suppose
![]() ${\sf S}\widetilde {n}$
occurs in
${\sf S}\widetilde {n}$
occurs in
![]() $\Lambda _k$
, then
$\Lambda _k$
, then
![]() $n \leq k+2$
.
$n \leq k+2$
.
Proof. We prove this by induction on k. In stage 0, we easily verify that the largest term of the form
![]() $\mathsf {S}\widetilde {n}$
can be at most
$\mathsf {S}\widetilde {n}$
can be at most
![]() $\mathsf {S} \widetilde 2$
.
$\mathsf {S} \widetilde 2$
.
Suppose, we have our desired estimate for
![]() $k-1$
, where
$k-1$
, where
![]() $k>0$
. We prove our estimate for k. Clearly, the
$k>0$
. We prove our estimate for k. Clearly, the
![]() $\mathsf {S}\widetilde {n}$
occurring in
$\mathsf {S}\widetilde {n}$
occurring in
![]() $\Lambda _{k-1}$
do satisfy our estimate. Moreover, all the
$\Lambda _{k-1}$
do satisfy our estimate. Moreover, all the
![]() $\widehat p$
added in stage k do not provide new elements of the form
$\widehat p$
added in stage k do not provide new elements of the form
![]() $\mathsf {S}\widetilde {n}$
. So, the only interesting case is the case where
$\mathsf {S}\widetilde {n}$
. So, the only interesting case is the case where
![]() $A_k$
is not of the form
$A_k$
is not of the form
![]() $\widehat p$
. Suppose it is not. The
$\widehat p$
. Suppose it is not. The
![]() ${\sf S}\widetilde {n}$
that are added are all sub-expressions of
${\sf S}\widetilde {n}$
that are added are all sub-expressions of
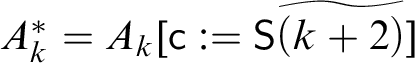 $ A^{\ast }_{k}= A_k[{\sf c} := {\sf S}\widetilde {(k+2)}]$
. So, we should focus on the largest such subterm. Suppose
$ A^{\ast }_{k}= A_k[{\sf c} := {\sf S}\widetilde {(k+2)}]$
. So, we should focus on the largest such subterm. Suppose
![]() ${\sf S}\widetilde {n} \preceq A^{\ast }_k$
. There are two possibilities:
${\sf S}\widetilde {n} \preceq A^{\ast }_k$
. There are two possibilities:
-
i.
 ${\sf S}\widetilde {n}\preceq A_k$
. In this case, we have
${\sf S}\widetilde {n}\preceq A_k$
. In this case, we have
 $n < {\lceil \mathsf {S}\widetilde {n} \rceil } \leq {\lceil A_k \rceil } \leq k+1 \leq k +2$
.
$n < {\lceil \mathsf {S}\widetilde {n} \rceil } \leq {\lceil A_k \rceil } \leq k+1 \leq k +2$
. -
ii.
 $n= k+2$
, since the subterm results from the substitution for c.
$n= k+2$
, since the subterm results from the substitution for c.
In each of the possible cases, we are done.□
Setting
![]() ${\sf gn}_2(A)$
to be the unique n such that
${\sf gn}_2(A)$
to be the unique n such that
![]() $A = B_n$
, we have found a monotonic Gödel numbering
$A = B_n$
, we have found a monotonic Gödel numbering
![]() ${\sf gn}_2$
.
${\sf gn}_2$
.
In order to show that
![]() ${\sf gn}_2$
satisfies M4(
${\sf gn}_2$
satisfies M4(
![]() $\overline {\cdot }$
), i.e., that
$\overline {\cdot }$
), i.e., that
![]() ${\sf gn}_2$
is strongly monotonic for efficient numerals, we prove the following auxiliary lemma.
${\sf gn}_2$
is strongly monotonic for efficient numerals, we prove the following auxiliary lemma.
Lemma 6.9. Suppose
![]() $\overline {p} \preceq A_k[\mathsf {c} := \overline r]$
, for some
$\overline {p} \preceq A_k[\mathsf {c} := \overline r]$
, for some
![]() $p,r \in \omega $
. Then,
$p,r \in \omega $
. Then,
![]() $p < 2^{k}(r+2)$
.
$p < 2^{k}(r+2)$
.
Proof. Let
![]() $p,r \in \omega $
be given such that
$p,r \in \omega $
be given such that
![]() $\overline {p} \preceq A_k[\mathsf {c} := \overline r]$
. Then (i)
$\overline {p} \preceq A_k[\mathsf {c} := \overline r]$
. Then (i)
![]() $\overline {p} \preceq A_k$
or (ii)
$\overline {p} \preceq A_k$
or (ii)
![]() $\overline {p}\preceq \overline r$
or (iii) there exists
$\overline {p}\preceq \overline r$
or (iii) there exists
![]() $t \preceq A_k$
containing
$t \preceq A_k$
containing
![]() $\mathsf {c}$
such that
$\mathsf {c}$
such that
![]() $\overline p = t[\mathsf {c} := \overline r]$
. In case (i), we have,
$\overline p = t[\mathsf {c} := \overline r]$
. In case (i), we have,
![]() $p < 2^{{\lceil \overline p \rceil }} \leq 2^{{\lceil A_k \rceil }} \leq 2^{k+1} \leq 2^{k}(r+2)$
. In case (ii), we have
$p < 2^{{\lceil \overline p \rceil }} \leq 2^{{\lceil A_k \rceil }} \leq 2^{k+1} \leq 2^{k}(r+2)$
. In case (ii), we have
![]() $p\leq r$
. So both in Case (i) and (ii), we find
$p\leq r$
. So both in Case (i) and (ii), we find
![]() $p< 2^{k}(r+2)$
.
$p< 2^{k}(r+2)$
.
Suppose we are are in case (iii). Since
![]() $\overline {r}$
and
$\overline {r}$
and
![]() $t[\mathsf {c} := \overline r]$
are efficient numerals, there exist
$t[\mathsf {c} := \overline r]$
are efficient numerals, there exist
![]() $k,j$
such that
$k,j$
such that
![]() $\overline {r}$
and t are of the following forms:
$\overline {r}$
and t are of the following forms:
-
•
 $\overline {r} = \mathsf {S}_{a_0}( \cdots \mathsf {S}_{a_k}({\sf 0}) \cdots )$
;
$\overline {r} = \mathsf {S}_{a_0}( \cdots \mathsf {S}_{a_k}({\sf 0}) \cdots )$
; -
•
 $t = \mathsf {S}_{c_0}( \cdots \mathsf {S}_{c_j}(\mathsf {c}) \cdots )$
;
$t = \mathsf {S}_{c_0}( \cdots \mathsf {S}_{c_j}(\mathsf {c}) \cdots )$
;
where
![]() $a_p, c_q \in \{ 1, 2 \}$
for each
$a_p, c_q \in \{ 1, 2 \}$
for each
![]() $p \leq k$
and
$p \leq k$
and
![]() $q \leq j$
, and
$q \leq j$
, and
![]() $\mathsf {S}_1(x) := \mathsf {S} (\mathsf {S}\mathsf {S} \mathsf {0} \times x)$
and
$\mathsf {S}_1(x) := \mathsf {S} (\mathsf {S}\mathsf {S} \mathsf {0} \times x)$
and
![]() $\mathsf {S}_2(x) := \mathsf {S} \mathsf {S} (\mathsf {S}\mathsf {S} \mathsf {0} \times x)$
. Moreover,
$\mathsf {S}_2(x) := \mathsf {S} \mathsf {S} (\mathsf {S}\mathsf {S} \mathsf {0} \times x)$
. Moreover,
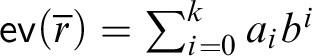 $\mathsf {ev}(\overline {r}) = \sum ^k_{i = 0} a_i b^i$
. Since
$\mathsf {ev}(\overline {r}) = \sum ^k_{i = 0} a_i b^i$
. Since
 $$ \begin{align*} t(\overline{r}) = \mathsf{S}_{c_0}( \cdots \mathsf{S}_{c_j}(\mathsf{S}_{a_0}( \cdots \mathsf{S}_{a_k}(\mathsf{0}) \cdots )) \cdots ), \end{align*} $$
$$ \begin{align*} t(\overline{r}) = \mathsf{S}_{c_0}( \cdots \mathsf{S}_{c_j}(\mathsf{S}_{a_0}( \cdots \mathsf{S}_{a_k}(\mathsf{0}) \cdots )) \cdots ), \end{align*} $$
we have
 $$ \begin{align*} p & = \mathsf{ev}(t(\overline{r}))\\ & = \sum^j_{i = 0} c_i 2^i + \sum^k_{i = 0} a_i 2^{i + j +1}\\ & = \sum^j_{i = 0} c_i 2^i + 2^{j +1} \sum^k_{i = 0} a_i 2^{i}\\ & < 2^{j+2} + 2^{j +1} r\\ & = 2^{j+1}(r+2). \end{align*} $$
$$ \begin{align*} p & = \mathsf{ev}(t(\overline{r}))\\ & = \sum^j_{i = 0} c_i 2^i + \sum^k_{i = 0} a_i 2^{i + j +1}\\ & = \sum^j_{i = 0} c_i 2^i + 2^{j +1} \sum^k_{i = 0} a_i 2^{i}\\ & < 2^{j+2} + 2^{j +1} r\\ & = 2^{j+1}(r+2). \end{align*} $$
For each
![]() $i \leq j$
, the expression
$i \leq j$
, the expression
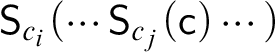 $\mathsf {S}_{c_i}( \cdots \mathsf {S}_{c_{j}}(\mathsf {c}) \cdots )$
is a subterm of
$\mathsf {S}_{c_i}( \cdots \mathsf {S}_{c_{j}}(\mathsf {c}) \cdots )$
is a subterm of
![]() $A_k$
. Since also
$A_k$
. Since also
![]() $\mathsf {c}$
is a subterm of
$\mathsf {c}$
is a subterm of
![]() $A_k$
, we have
$A_k$
, we have
![]() $j+2 \leq {\lceil A_k \rceil } \leq k+1$
. We thus conclude that
$j+2 \leq {\lceil A_k \rceil } \leq k+1$
. We thus conclude that
![]() $p < 2^{k}(r+2)$
.□
$p < 2^{k}(r+2)$
.□
We now show that
![]() ${\sf gn}_2$
satisfies M4(
${\sf gn}_2$
satisfies M4(
![]() $\overline {\cdot }$
).
$\overline {\cdot }$
).
Lemma 6.10.
![]() $m < {\sf gn}_2( \overline {m} )$
for all
$m < {\sf gn}_2( \overline {m} )$
for all
![]() $m \in \omega $
.
$m \in \omega $
.
Proof. Let
![]() $\overline m$
be added in stage k, i.e.,
$\overline m$
be added in stage k, i.e.,
![]() $\overline m \in \Lambda _k \setminus \Lambda _{k-1}$
. We then have
$\overline m \in \Lambda _k \setminus \Lambda _{k-1}$
. We then have
![]() $B_{{\mathfrak n}(k) - \ell + j} = \overline {m}$
, for some
$B_{{\mathfrak n}(k) - \ell + j} = \overline {m}$
, for some
![]() $j < \ell $
. (We use here the fact that no filler is of the form
$j < \ell $
. (We use here the fact that no filler is of the form
![]() $\overline {m}$
). We have
$\overline {m}$
). We have
![]() $\ell \leq 3k + 8$
, as noted in (*) subsequent to presenting our construction. Hence,
$\ell \leq 3k + 8$
, as noted in (*) subsequent to presenting our construction. Hence,
We moreover have
 $\overline {m} \preceq A_k [{\sf c} := {\sf S}\widetilde {(k+2)}]$
. Since
$\overline {m} \preceq A_k [{\sf c} := {\sf S}\widetilde {(k+2)}]$
. Since
 ${\sf S}\widetilde {(k+2)} = \overline {2^{k+2}}$
we get
${\sf S}\widetilde {(k+2)} = \overline {2^{k+2}}$
we get
by Lemma 6.9. It is easy to check that
![]() $3 \cdot 2^{k+1} < 2^{2k+4} - 3k - 7$
. Hence,
$3 \cdot 2^{k+1} < 2^{2k+4} - 3k - 7$
. Hence,
![]() $m < {\sf gn}_2( \overline {m} )$
.□
$m < {\sf gn}_2( \overline {m} )$
.□
Even though
![]() ${\sf gn}_2$
cannot be self-referential for efficient numerals by Lemma 6.1, the following modification holds.
${\sf gn}_2$
cannot be self-referential for efficient numerals by Lemma 6.1, the following modification holds.
Lemma 6.11. Consider any A such that c occurs in A. Then there exists n such that
![]() ${\sf gn}_2(A[{\sf c}:= \overline {n}]) = n^2$
.
${\sf gn}_2(A[{\sf c}:= \overline {n}]) = n^2$
.
Proof. Suppose c occurs in A. Let
![]() $A := A_k$
. The only thing we have to show is that
$A := A_k$
. The only thing we have to show is that
![]() $A^{\ast }_k$
is not in
$A^{\ast }_k$
is not in
![]() $\Lambda _{k-1}$
. This is certainly true for
$\Lambda _{k-1}$
. This is certainly true for
![]() $k=0$
. Suppose
$k=0$
. Suppose
![]() $k>0$
. We note that
$k>0$
. We note that
 ${\sf S}\widetilde {(k+2)}$
occurs in
${\sf S}\widetilde {(k+2)}$
occurs in
![]() $A^{\ast }_k$
. So, it is sufficient to show that
$A^{\ast }_k$
. So, it is sufficient to show that
 ${\sf S}\widetilde {(k+2)}$
does not occur in
${\sf S}\widetilde {(k+2)}$
does not occur in
![]() $\Lambda _{k-1}$
. By Lemma 6.8, whenever
$\Lambda _{k-1}$
. By Lemma 6.8, whenever
![]() $\mathsf {S}\widetilde {n}$
occurs in
$\mathsf {S}\widetilde {n}$
occurs in
![]() $\Lambda _{k-1}$
, we have
$\Lambda _{k-1}$
, we have
![]() $n \leq k+1$
. We may conclude that
$n \leq k+1$
. We may conclude that
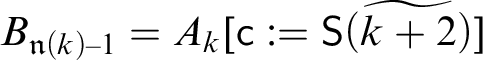 $B_{{\mathfrak n}(k)-1} = A_k[\mathsf {c} := \mathsf {S}(\widetilde {k+2})]$
. Let
$B_{{\mathfrak n}(k)-1} = A_k[\mathsf {c} := \mathsf {S}(\widetilde {k+2})]$
. Let
![]() $n := 2^{k+2}$
. Since
$n := 2^{k+2}$
. Since
![]() $n^2 = {\mathfrak n}(k)-1$
and
$n^2 = {\mathfrak n}(k)-1$
and
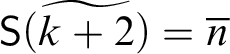 $\mathsf {S}(\widetilde {k+2}) = \overline {n}$
, we are done.□
$\mathsf {S}(\widetilde {k+2}) = \overline {n}$
, we are done.□
We now can immediately derive the Strong Diagonal Lemma.
Proof of Lemma 6.3
Let
![]() $C(x)$
be given and set
$C(x)$
be given and set
![]() $A := C[x := \mathsf {c} \times \mathsf {c}]$
. By Lemma 6.11 there exists
$A := C[x := \mathsf {c} \times \mathsf {c}]$
. By Lemma 6.11 there exists
![]() $n \in \omega $
such that
$n \in \omega $
such that
![]() ${\sf gn}_2(A[\mathsf {c} := \overline {n}]) = n^2$
. Set
${\sf gn}_2(A[\mathsf {c} := \overline {n}]) = n^2$
. Set
![]() $t := \overline {n} \times \overline {n}$
. We then have
$t := \overline {n} \times \overline {n}$
. We then have
![]() $A[\mathsf {c} := \overline {n}] = C[x := t]$
. Moreover
$A[\mathsf {c} := \overline {n}] = C[x := t]$
. Moreover
![]() $\mathsf {R}_{\mathcal {L}} \vdash t = \underline {n^2}$
. Hence
$\mathsf {R}_{\mathcal {L}} \vdash t = \underline {n^2}$
. Hence
 ${\mathsf {R}_{\mathcal {L}} \vdash t = \underline {{\sf gn}_2(C[x := t])}}$
.□
${\mathsf {R}_{\mathcal {L}} \vdash t = \underline {{\sf gn}_2(C[x := t])}}$
.□
By suitably adapting the above construction, we obtain a numbering which is monotonic with respect to the sub-string relation, satisfies M4(
![]() $\overline {\cdot }$
) and provides the existence of m-self-referential sentences for
$\overline {\cdot }$
) and provides the existence of m-self-referential sentences for
![]() $\mathcal {L}$
(i.e., satisfies Lemma 6.3). We leave the details to the diligent reader.
$\mathcal {L}$
(i.e., satisfies Lemma 6.3). We leave the details to the diligent reader.
7 Computational Constraints
In addition to requiring monotonicity, other adequacy constraints for Gödel numberings can be extracted from the literature. Let
![]() $\mathfrak {Po}$
,
$\mathfrak {Po}$
,
![]() $\mathfrak {El}$
and
$\mathfrak {El}$
and
![]() $\mathfrak {Pr}$
denote the classes of p-time, (Kalmár) elementary and primitive recursive functions respectively. As usual, these classes can be extended to relations and partial functions on
$\mathfrak {Pr}$
denote the classes of p-time, (Kalmár) elementary and primitive recursive functions respectively. As usual, these classes can be extended to relations and partial functions on
![]() $\omega $
as follows.
$\omega $
as follows.
Definition 7.1. Let
![]() $\mathcal {C} \in \{\mathfrak {Po},\mathfrak {El},\mathfrak {Pr}\}$
. We say that a subset of
$\mathcal {C} \in \{\mathfrak {Po},\mathfrak {El},\mathfrak {Pr}\}$
. We say that a subset of
![]() $\omega ^k$
or a relation on
$\omega ^k$
or a relation on
![]() $\omega $
is in
$\omega $
is in
![]() $\mathcal {C}$
, if its characteristic function is in
$\mathcal {C}$
, if its characteristic function is in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Let
![]() $R \subseteq \omega ^k$
be given. We say that a function
$R \subseteq \omega ^k$
be given. We say that a function
![]() $f \colon R \to \omega $
is in
$f \colon R \to \omega $
is in
![]() $\mathcal {C}$
, if the total function
$\mathcal {C}$
, if the total function
![]() $f' \colon \omega ^k \to \omega $
given by
$f' \colon \omega ^k \to \omega $
given by
 $$ \begin{align*} f'(m_1, \ldots, m_k) := \begin{cases} f(m_1, \ldots, m_k) +1 & \text{if } m_1, \ldots, m_k \in R;\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} f'(m_1, \ldots, m_k) := \begin{cases} f(m_1, \ldots, m_k) +1 & \text{if } m_1, \ldots, m_k \in R;\\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
is in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Reasonable numberings are commonly required to represent certain syntactic relations and operations by primitive recursive relations and operations on
![]() $\omega $
(see [Reference Halbach8, sec. 5.1]). The usual definitions of the syntactic relations (i.e., their extensions)
$\omega $
(see [Reference Halbach8, sec. 5.1]). The usual definitions of the syntactic relations (i.e., their extensions)
![]() $\mathsf {Var}_{\mathcal {L}}$
(“is a variable”),
$\mathsf {Var}_{\mathcal {L}}$
(“is a variable”),
![]() $\mathsf {Ter}_{\mathcal {L}}$
(“is a term”),
$\mathsf {Ter}_{\mathcal {L}}$
(“is a term”),
![]() $\mathsf {AtFml}_{\mathcal {L}}$
(“is an atomic formula”),
$\mathsf {AtFml}_{\mathcal {L}}$
(“is an atomic formula”),
![]() $\mathsf {Fml}_{\mathcal {L}}$
(“is an a formula”),
$\mathsf {Fml}_{\mathcal {L}}$
(“is an a formula”),
![]() $\mathsf {Sent}_{\mathcal {L}}$
(“is a sentence”), “is a free variable in,” “is a
$\mathsf {Sent}_{\mathcal {L}}$
(“is a sentence”), “is a free variable in,” “is a
![]() $\mathsf {PA}$
-derivation of” etc., are either explicit or of simple recursive structure. Adequate numberings may be required to preserve this simple algorithmic nature, in virtue of representing these relations by primitive recursive relations on
$\mathsf {PA}$
-derivation of” etc., are either explicit or of simple recursive structure. Adequate numberings may be required to preserve this simple algorithmic nature, in virtue of representing these relations by primitive recursive relations on
![]() $\omega $
. More precisely, for any adequate numbering
$\omega $
. More precisely, for any adequate numbering
![]() $\xi $
, the characteristic functions of the sets of
$\xi $
, the characteristic functions of the sets of
![]() $\xi $
-codes of
$\xi $
-codes of
![]() $\mathsf {Var}_{\mathcal {L}}$
,
$\mathsf {Var}_{\mathcal {L}}$
,
![]() $\mathsf {Ter}_{\mathcal {L}}$
, etc. are required to be primitive recursive. A similar constraint can be extracted for the syntactic functions
$\mathsf {Ter}_{\mathcal {L}}$
, etc. are required to be primitive recursive. A similar constraint can be extracted for the syntactic functions
![]() $\dot {=}$
,
$\dot {=}$
,
![]() $\dot \neg $
,
$\dot \neg $
,
![]() $\dot \wedge $
,
$\dot \wedge $
,
![]() $\dot \vee $
,
$\dot \vee $
,
![]() $\dot \forall $
,
$\dot \forall $
,
![]() $\dot \exists $
,
$\dot \exists $
,
![]() $\dot {\mathsf {S}}$
,
$\dot {\mathsf {S}}$
,
![]() $\dot {+}$
,
$\dot {+}$
,
![]() $\dot \times $
,
$\dot \times $
,
![]() $\mathsf {Sub}$
etc., where for instance,
$\mathsf {Sub}$
etc., where for instance,
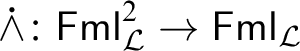 $\dot {\wedge } \colon \mathsf {Fml}_{\mathcal {L}}^2 \to \mathsf {Fml}_{\mathcal {L}}$
maps a pair
$\dot {\wedge } \colon \mathsf {Fml}_{\mathcal {L}}^2 \to \mathsf {Fml}_{\mathcal {L}}$
maps a pair
![]() $\langle A,B \rangle $
of formulæ to the conjunction
$\langle A,B \rangle $
of formulæ to the conjunction
![]() $A \wedge B$
,
$A \wedge B$
,
![]() $\dot {\forall } \colon \mathsf {Fml}_{\mathcal {L}} \times \mathsf {Var}_{\mathcal {L}} \to \mathsf {Fml}_{\mathcal {L}}$
maps a pair
$\dot {\forall } \colon \mathsf {Fml}_{\mathcal {L}} \times \mathsf {Var}_{\mathcal {L}} \to \mathsf {Fml}_{\mathcal {L}}$
maps a pair
![]() $\langle A,x \rangle $
to the universal formula
$\langle A,x \rangle $
to the universal formula
![]() $\forall x A$
, etc., and where
$\forall x A$
, etc., and where
![]() $\mathsf {Sub}(A,x,t)$
is the result of substituting the term t for the variable x in the formula A. Once again, adequate numberings may be required to represent these syntactic functions by primitive recursive functions on
$\mathsf {Sub}(A,x,t)$
is the result of substituting the term t for the variable x in the formula A. Once again, adequate numberings may be required to represent these syntactic functions by primitive recursive functions on
![]() $\omega $
. Finally, the standard and the efficient numeral function may be required to be represented primitive recursively.
$\omega $
. Finally, the standard and the efficient numeral function may be required to be represented primitive recursively.
The arithmetisation of syntax in weaker theories, like Buss’
![]() ${\sf S}^1_2$
and
${\sf S}^1_2$
and
![]() $\mathrm{I}\Delta _0+\Omega _1$
, requires representation of the syntactic relations and functions in weaker theories.Footnote
12
A closer inspection of what is going on shows that, in the presence of a reasonable Gödel numbering like the one based on the length-first ordering, the syntactic relations and functions can be made p-time without extra effort. See [Reference Buss2, Reference Hájek and Pudlák7]. The Gödel numberings we construct here fit most naturally in the intermediate function class
$\mathrm{I}\Delta _0+\Omega _1$
, requires representation of the syntactic relations and functions in weaker theories.Footnote
12
A closer inspection of what is going on shows that, in the presence of a reasonable Gödel numbering like the one based on the length-first ordering, the syntactic relations and functions can be made p-time without extra effort. See [Reference Buss2, Reference Hájek and Pudlák7]. The Gödel numberings we construct here fit most naturally in the intermediate function class
![]() $\mathfrak {El}$
.
$\mathfrak {El}$
.
Definition 7.2. Let
![]() $\mathcal {C} \in \{\mathfrak {Po},\mathfrak {El},\mathfrak {Pr}\}$
and let
$\mathcal {C} \in \{\mathfrak {Po},\mathfrak {El},\mathfrak {Pr}\}$
and let
![]() $\nu $
be a numeral function. We say that a numbering
$\nu $
be a numeral function. We say that a numbering
![]() $\xi $
of
$\xi $
of
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $\mathcal {C},\nu $
-adequate, if
$\mathcal {C},\nu $
-adequate, if
-
1. the set of
 $\xi $
-codes of each syntactic relation specified above is in
$\xi $
-codes of each syntactic relation specified above is in
 $\mathcal {C}$
;
$\mathcal {C}$
; -
2. the
 $\xi $
-tracking function of each syntactic function specified above is in
$\xi $
-tracking function of each syntactic function specified above is in
 $\mathcal {C}$
, i.e., for each k-ary syntactic function f, the function
$\mathcal {C}$
, i.e., for each k-ary syntactic function f, the function
 $\xi (f)$
given by
$\xi (f)$
given by
 $\xi (f)(m_1, \ldots , m_k) := \xi (f(\xi ^{-1}(m_1), \ldots , \xi ^{-1}(m_k) ) )$
is in
$\xi (f)(m_1, \ldots , m_k) := \xi (f(\xi ^{-1}(m_1), \ldots , \xi ^{-1}(m_k) ) )$
is in
 $\mathcal {C}$
; and
$\mathcal {C}$
; and -
3. the function
 $\xi \circ \nu $
is in
$\xi \circ \nu $
is in
 ${\mathcal C}$
.
${\mathcal C}$
.
We say that
![]() $\xi $
is
$\xi $
is
![]() ${\mathcal C}$
-adequate iff (
${\mathcal C}$
-adequate iff (
![]() ${\mathcal C}\in \{ \mathfrak {El},\mathfrak {Pr} \}$
and
${\mathcal C}\in \{ \mathfrak {El},\mathfrak {Pr} \}$
and
![]() $\xi $
is both
$\xi $
is both
![]() ${\mathcal C},(\overline \cdot )$
-adequate and
${\mathcal C},(\overline \cdot )$
-adequate and
![]() ${\mathcal C},(\underline \cdot )$
-adequate) or (
${\mathcal C},(\underline \cdot )$
-adequate) or (
![]() ${\mathcal C} = \mathfrak {Po}$
and
${\mathcal C} = \mathfrak {Po}$
and
![]() $\xi $
is
$\xi $
is
![]() ${\mathcal C},(\overline \cdot )$
-adequate).
${\mathcal C},(\overline \cdot )$
-adequate).
The definition of
![]() ${\mathcal C}$
-adequate is somewhat awkward since, for a good numbering like the one based on the length-first ordering, the function
${\mathcal C}$
-adequate is somewhat awkward since, for a good numbering like the one based on the length-first ordering, the function
![]() $\xi \circ (\underline \cdot )$
will be exponential. This is the reason for the use of efficient numerals in the context of weak theories. It would be interesting, and conceivably genuinely useful, to explore whether there are
$\xi \circ (\underline \cdot )$
will be exponential. This is the reason for the use of efficient numerals in the context of weak theories. It would be interesting, and conceivably genuinely useful, to explore whether there are
![]() $\mathfrak {Po}$
-adequate numberings
$\mathfrak {Po}$
-adequate numberings
![]() $\xi $
for which
$\xi $
for which
![]() $\xi \circ (\underline \cdot )$
is p-time.
$\xi \circ (\underline \cdot )$
is p-time.
Remark 7.3. Feferman’s Gödel numbering, say
![]() ${\sf fef}$
, in Reference Feferman[4] is a good example to reflect on. The tracking functions are all elementary. The code for 0 is 3 and the code for successor is 7. We have
${\sf fef}$
, in Reference Feferman[4] is a good example to reflect on. The tracking functions are all elementary. The code for 0 is 3 and the code for successor is 7. We have
![]() ${\sf fef}({\sf S}t) = 2^7\cdot 3^{{\sf fef}(t)}$
. So, the numeral function for standard numerals will be superexponential and not elementary. Similarly, for efficient numerals.
${\sf fef}({\sf S}t) = 2^7\cdot 3^{{\sf fef}(t)}$
. So, the numeral function for standard numerals will be superexponential and not elementary. Similarly, for efficient numerals.
Suppose we replace Feferman’s coding for the terms by an efficient coding but leave his code formation for formulæ in place (taking appropriate measures to insure disjointness). Then, we obtain an
![]() $\mathfrak {El}$
-adequate Gödel numbering
$\mathfrak {El}$
-adequate Gödel numbering
![]() $\digamma $
. However, we still would have:
$\digamma $
. However, we still would have:
![]() $\digamma (\neg \, A ) := 2\cdot 3^{\,\digamma (A)}$
. This means that, if we iterate negations, we run up an exponential tower.
$\digamma (\neg \, A ) := 2\cdot 3^{\,\digamma (A)}$
. This means that, if we iterate negations, we run up an exponential tower.
The example of
![]() $\digamma $
illustrates that it is possible that a Gödel numbering is
$\digamma $
illustrates that it is possible that a Gödel numbering is
![]() $\mathfrak {El}$
-adequate but not elementary in the length of expressions. This observation suggests that, where p-time and primitive recursive satisfy a certain equilibrium, possibly elementary does not. If the tracking function for function application is exponential, the codes of numerals, both standard and efficient, grow too fast. So, the tracking function for function application is severely constrained. But if this function is so slow, it seems a certain imbalance to make other forms of application much faster. So, why is this numbering not already
$\mathfrak {El}$
-adequate but not elementary in the length of expressions. This observation suggests that, where p-time and primitive recursive satisfy a certain equilibrium, possibly elementary does not. If the tracking function for function application is exponential, the codes of numerals, both standard and efficient, grow too fast. So, the tracking function for function application is severely constrained. But if this function is so slow, it seems a certain imbalance to make other forms of application much faster. So, why is this numbering not already
![]() $\mathfrak {Po}$
-adequate? …
$\mathfrak {Po}$
-adequate? …
We now introduce a useful proof-theoretical characterisation of the classes
![]() $\mathfrak {Po}$
,
$\mathfrak {Po}$
,
![]() $\mathfrak {El}$
and
$\mathfrak {El}$
and
![]() $\mathfrak {Pr}$
. This will result in a specification of the theories in which
$\mathfrak {Pr}$
. This will result in a specification of the theories in which
![]() ${\mathcal C}$
-adequate numberings permit the arithmetisation of syntax. To this end, we first introduce so-called provably recursive functions.
${\mathcal C}$
-adequate numberings permit the arithmetisation of syntax. To this end, we first introduce so-called provably recursive functions.
Definition 7.4. Let T be an
![]() $\mathcal {L}$
-theory. A function
$\mathcal {L}$
-theory. A function
![]() $f \colon \omega ^k \to \omega $
is called
$f \colon \omega ^k \to \omega $
is called
![]() $\Sigma _n$
-definable in T, if there exists a
$\Sigma _n$
-definable in T, if there exists a
![]() $\Sigma _n$
-formula
$\Sigma _n$
-formula
![]() $A(x_1, \ldots , x_k,y)$
such that
$A(x_1, \ldots , x_k,y)$
such that
-
•
 $\mathbb {N} \models A(\underline {m_1}, \ldots , \underline {m_k},\underline {p})$
iff
$\mathbb {N} \models A(\underline {m_1}, \ldots , \underline {m_k},\underline {p})$
iff
 $f(m_1, \ldots , m_k)=p$
, for all
$f(m_1, \ldots , m_k)=p$
, for all
 $m_1, \ldots , m_k,p \in \omega $
and
$m_1, \ldots , m_k,p \in \omega $
and -
•
 $T \vdash \forall x_1, \ldots , x_k \exists ! y\, A(x_1, \ldots , x_k,y)$
.
$T \vdash \forall x_1, \ldots , x_k \exists ! y\, A(x_1, \ldots , x_k,y)$
.
The function f is called provably recursive in T if f is
![]() $\Sigma _1$
-definable in T.
$\Sigma _1$
-definable in T.
Remark 7.5. We note that there is some awkwardness to this definition since the provably recursive functions of all
![]() $\Sigma _1$
-unsound theories extending
$\Sigma _1$
-unsound theories extending
![]() ${\sf EA}$
, like
${\sf EA}$
, like
![]() $\mathrm{I}\Sigma _1+{\sf incon}({\sf ZF})$
, are precisely all recursive functions. This creates the mistaken impression that, e.g.,
$\mathrm{I}\Sigma _1+{\sf incon}({\sf ZF})$
, are precisely all recursive functions. This creates the mistaken impression that, e.g.,
![]() $\mathrm{I}\Sigma _1+{\sf incon}({\sf ZF})$
is stronger than
$\mathrm{I}\Sigma _1+{\sf incon}({\sf ZF})$
is stronger than
![]() ${\sf PA}$
.
${\sf PA}$
.
With an extra argument, one can show that this malaise persists even when we replace ‘
 $\mathbb N \models A(\underline {m_1}, \ldots , \underline {m_k},\underline {p})$
’ in the definition by ‘
$\mathbb N \models A(\underline {m_1}, \ldots , \underline {m_k},\underline {p})$
’ in the definition by ‘
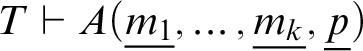 $T \vdash A(\underline {m_1}, \ldots , \underline {m_k},\underline {p})$
’.
$T \vdash A(\underline {m_1}, \ldots , \underline {m_k},\underline {p})$
’.
We are unaware of attempts to address this awkwardness.
The classes
![]() $\mathfrak {El}$
and
$\mathfrak {El}$
and
![]() $\mathfrak {Pr}$
can now be characterised as exactly the functions which are provably recursive in a certain theory. The situation for the p-time computable functions is a bit more delicate.
$\mathfrak {Pr}$
can now be characterised as exactly the functions which are provably recursive in a certain theory. The situation for the p-time computable functions is a bit more delicate.
Theorem 7.6. Let f be a number-theoretic function. Then
-
• f is p-time iff f is
 $\Sigma _1^{\sf b}$
-definable in
$\Sigma _1^{\sf b}$
-definable in
 $\mathsf {S}^1_2$
, where
$\mathsf {S}^1_2$
, where
 $\Sigma _1^{\sf b}$
is the special formula class introduced in Reference Buss[2];
$\Sigma _1^{\sf b}$
is the special formula class introduced in Reference Buss[2]; -
• f is elementary iff f is provably recursive in
 $\mathsf {EA}$
;
$\mathsf {EA}$
; -
• f is primitive recursive iff f is is provably recursive in
 $\mathsf {I \Sigma _1}$
.
$\mathsf {I \Sigma _1}$
.
Hence, for example, for any
![]() $\mathfrak {Pr}$
-adequate numbering
$\mathfrak {Pr}$
-adequate numbering
![]() $\xi $
there exists a
$\xi $
there exists a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\mathsf {Conj}(x,y,z) \in \mathcal {L}$
, such that
$\mathsf {Conj}(x,y,z) \in \mathcal {L}$
, such that
-
•
 $\mathbb {N} \models \mathsf {Conj}(\underline {\xi (A)},\underline {\xi (B)},\underline {\xi (C)}) $
iff
$\mathbb {N} \models \mathsf {Conj}(\underline {\xi (A)},\underline {\xi (B)},\underline {\xi (C)}) $
iff
 $C = A \wedge B$
, for all formulæ
$C = A \wedge B$
, for all formulæ
 $A,B,C \in \mathcal {L}$
;
$A,B,C \in \mathcal {L}$
; -
•
 $\mathsf {I \Sigma _1} \vdash \forall x,y \exists ! z \, \mathsf {Conj}(x,y,z) $
;
$\mathsf {I \Sigma _1} \vdash \forall x,y \exists ! z \, \mathsf {Conj}(x,y,z) $
;
i.e., the
![]() $\xi $
-tracking function of
$\xi $
-tracking function of
![]() $\dot \wedge $
is provably recursive in
$\dot \wedge $
is provably recursive in
![]() $\mathsf {I \Sigma _1}$
. Indeed, the representation of
$\mathsf {I \Sigma _1}$
. Indeed, the representation of
![]() $\dot \wedge $
by a provably recursive function (in
$\dot \wedge $
by a provably recursive function (in
![]() $\mathsf {PA}$
) is required as a necessary condition for reasonable numberings in [Reference Halbach8, p. 33]. As a result of the above theorem,
$\mathsf {PA}$
) is required as a necessary condition for reasonable numberings in [Reference Halbach8, p. 33]. As a result of the above theorem,
![]() $\mathfrak {Pr}$
-adequate numberings allow a large portion of syntax to be formalised in the theory
$\mathfrak {Pr}$
-adequate numberings allow a large portion of syntax to be formalised in the theory
![]() $\mathsf {I \Sigma _1}$
and, similarly, for
$\mathsf {I \Sigma _1}$
and, similarly, for
![]() $\mathfrak {El}$
and EA and for
$\mathfrak {El}$
and EA and for
![]() $\mathfrak {Po}$
and
$\mathfrak {Po}$
and
![]() ${\sf S}^1_2$
.Footnote
13
${\sf S}^1_2$
.Footnote
13
Recall that the constructions of the numberings
![]() ${\sf gn}_0$
,
${\sf gn}_0$
,
![]() ${\sf gn}_1$
and
${\sf gn}_1$
and
![]() ${\sf gn}_2$
rely on an enumeration
${\sf gn}_2$
rely on an enumeration
![]() $(A_n)_{n \in \omega }$
of
$(A_n)_{n \in \omega }$
of
![]() $\mathcal {L}$
-expressions. Thus far, assuming
$\mathcal {L}$
-expressions. Thus far, assuming
![]() $(A_n)_{n \in \omega }$
to be effective has sufficed to ensure the effectiveness of the resulting numberings
$(A_n)_{n \in \omega }$
to be effective has sufficed to ensure the effectiveness of the resulting numberings
![]() ${\sf gn}_0$
,
${\sf gn}_0$
,
![]() ${\sf gn}_1$
and
${\sf gn}_1$
and
![]() ${\sf gn}_2$
. Since no further computational constraint has been imposed on
${\sf gn}_2$
. Since no further computational constraint has been imposed on
![]() $(A_n)_{n \in \omega }$
, there is however no reason to expect these numberings to be even
$(A_n)_{n \in \omega }$
, there is however no reason to expect these numberings to be even
![]() $\mathfrak {Pr}$
-adequate. In the remainder of this paper, we will assume that the enumeration
$\mathfrak {Pr}$
-adequate. In the remainder of this paper, we will assume that the enumeration
![]() $(A_n)_{n \in \omega }$
(without repetitions) employed in the constructions of the numberings
$(A_n)_{n \in \omega }$
(without repetitions) employed in the constructions of the numberings
![]() ${\sf gn}_0$
,
${\sf gn}_0$
,
![]() ${\sf gn}_1$
and
${\sf gn}_1$
and
![]() ${\sf gn}_2$
is obtained from a standard numbering which is
${\sf gn}_2$
is obtained from a standard numbering which is
![]() $\mathfrak {El}$
-adequate, such that
$\mathfrak {El}$
-adequate, such that
![]() $(A_n)_{n \in \omega }$
also satisfies the remaining assumptions imposed in the constructions of
$(A_n)_{n \in \omega }$
also satisfies the remaining assumptions imposed in the constructions of
![]() ${\sf gn}_0$
,
${\sf gn}_0$
,
![]() ${\sf gn}_1$
and
${\sf gn}_1$
and
![]() ${\sf gn}_2$
respectively. That is,
${\sf gn}_2$
respectively. That is,
![]() $(A_n)_{n \in \omega } = ( \mathsf {gn}_{\ast }^{-1}(n))_{n \in \omega }$
, for some suitable standard numbering
$(A_n)_{n \in \omega } = ( \mathsf {gn}_{\ast }^{-1}(n))_{n \in \omega }$
, for some suitable standard numbering
![]() $\mathsf {gn}_{\ast }$
.
$\mathsf {gn}_{\ast }$
.
Under the assumption that
![]() $(A_n)_{n \in \omega }$
is
$(A_n)_{n \in \omega }$
is
![]() $\mathfrak {El}$
-adequate, we now show that the numberings
$\mathfrak {El}$
-adequate, we now show that the numberings
![]() ${\sf gn}_0$
,
${\sf gn}_0$
,
![]() ${\sf gn}_1$
and
${\sf gn}_1$
and
![]() ${\sf gn}_2$
are
${\sf gn}_2$
are
![]() $\mathfrak {El}$
-adequate, and, thus, also
$\mathfrak {El}$
-adequate, and, thus, also
![]() $\mathfrak {Pr}$
-adequate. This will follow from the fact that the standard numbering
$\mathfrak {Pr}$
-adequate. This will follow from the fact that the standard numbering
![]() $\mathsf {gn}_{\ast }$
is
$\mathsf {gn}_{\ast }$
is
![]() $\mathfrak {El}$
-adequate and that
$\mathfrak {El}$
-adequate and that
![]() $\mathsf {gn}_{\ast }$
,
$\mathsf {gn}_{\ast }$
,
![]() ${\sf gn}_0$
,
${\sf gn}_0$
,
![]() ${\sf gn}_1$
and
${\sf gn}_1$
and
![]() ${\sf gn}_2$
are elementarily intertranslatable. Let
${\sf gn}_2$
are elementarily intertranslatable. Let
 $\mathsf {tr}_{i,j} \colon \mathsf {gn}_j(\mathcal {L}) \to \omega $
be the translation function, given by
$\mathsf {tr}_{i,j} \colon \mathsf {gn}_j(\mathcal {L}) \to \omega $
be the translation function, given by
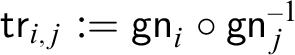 $\mathsf {tr}_{i,j} := \mathsf {gn}_i \circ \mathsf {gn}_j^{-1}$
, for each
$\mathsf {tr}_{i,j} := \mathsf {gn}_i \circ \mathsf {gn}_j^{-1}$
, for each
![]() $i, j \in \{ \ast ,0,1,2 \}$
. We then have:
$i, j \in \{ \ast ,0,1,2 \}$
. We then have:
Lemma 7.7. For each
![]() $i, j \in \{ \ast ,0,1,2 \}$
, the translation functions
$i, j \in \{ \ast ,0,1,2 \}$
, the translation functions
![]() $\mathsf {tr}_{i,j}$
are elementary.
$\mathsf {tr}_{i,j}$
are elementary.
Proof. We treat the case of the intertranslation of
![]() $\ast $
and 2. To show that
$\ast $
and 2. To show that
![]() $\mathsf {tr}_{\ast ,i}$
and
$\mathsf {tr}_{\ast ,i}$
and
![]() $\mathsf {tr}_{i,\ast }$
are elementary for
$\mathsf {tr}_{i,\ast }$
are elementary for
![]() $i = 0,1$
proceeds similarly. From these cases we can conclude that
$i = 0,1$
proceeds similarly. From these cases we can conclude that
![]() $\mathsf {tr}_{i,j}$
is elementary for
$\mathsf {tr}_{i,j}$
is elementary for
![]() $i,j \leq 2$
.
$i,j \leq 2$
.
We use the fact that the coding machinery for finite sequences can be developed in
![]() $\mathfrak {El}$
(see, for example, [Reference Schwichtenberg and Wainer26, chap. 2]). Let
$\mathfrak {El}$
(see, for example, [Reference Schwichtenberg and Wainer26, chap. 2]). Let
![]() $\# \colon \omega ^{< \omega } \to \omega $
be an elementary coding function of finite sequences and let
$\# \colon \omega ^{< \omega } \to \omega $
be an elementary coding function of finite sequences and let
![]() ${\sf lh}$
be the length function. Let
${\sf lh}$
be the length function. Let
![]() $g \colon \omega \to \omega $
serve as a parameter. We define the function
$g \colon \omega \to \omega $
serve as a parameter. We define the function
![]() $\sigma _g \colon \omega \to \omega $
, by setting
$\sigma _g \colon \omega \to \omega $
, by setting
![]() $\sigma _g(k) := \# \langle i_0, \ldots , i_{\ell -1} \rangle $
, where
$\sigma _g(k) := \# \langle i_0, \ldots , i_{\ell -1} \rangle $
, where
![]() $A_{i_0}, \ldots , A_{i_{\ell -1}}$
are exactly the sub-expressions of
$A_{i_0}, \ldots , A_{i_{\ell -1}}$
are exactly the sub-expressions of
 $A_k [{\sf c} := {\sf S}\widetilde {(k+2)}]$
which are not of the form
$A_k [{\sf c} := {\sf S}\widetilde {(k+2)}]$
which are not of the form
![]() $\widehat {m}$
such that
$\widehat {m}$
such that
![]() $g(n) \neq i_j$
for all
$g(n) \neq i_j$
for all
![]() $n < {\mathfrak n}(k-1)$
and
$n < {\mathfrak n}(k-1)$
and
![]() $j < {\sf lh}(\sigma _g(k)) = \ell $
. Since
$j < {\sf lh}(\sigma _g(k)) = \ell $
. Since
![]() ${\mathfrak n} \in \mathfrak {El}$
and
${\mathfrak n} \in \mathfrak {El}$
and
![]() ${\sf gn}_{\ast }$
is
${\sf gn}_{\ast }$
is
![]() $\mathfrak {El}$
-adequate,
$\mathfrak {El}$
-adequate,
![]() $g \in \mathfrak {El}$
implies
$g \in \mathfrak {El}$
implies
![]() $\sigma \in \mathfrak {El}$
, by the usual closure properties of elementary functions. In case that
$\sigma \in \mathfrak {El}$
, by the usual closure properties of elementary functions. In case that
![]() $g := \mathsf {tr}_{2,\ast }$
, the last clause is equivalent to
$g := \mathsf {tr}_{2,\ast }$
, the last clause is equivalent to
![]() $A_{i_j} \notin \Lambda _{k-1}$
for each
$A_{i_j} \notin \Lambda _{k-1}$
for each
![]() $j < \ell $
.
$j < \ell $
.
Set
![]() $\sigma := \sigma _{\mathsf {tr}_{2,\ast }}$
. For any
$\sigma := \sigma _{\mathsf {tr}_{2,\ast }}$
. For any
![]() $n \in \omega $
, we compute
$n \in \omega $
, we compute
![]() $\mathsf {tr}_{2,\ast }(n)$
by course-of-values recursion as follows. As usual, we will take the empty sum to be 0.
$\mathsf {tr}_{2,\ast }(n)$
by course-of-values recursion as follows. As usual, we will take the empty sum to be 0.
Compute the smallest k (
![]() ${\leq } n$
) such that
${\leq } n$
) such that
![]() $n\leq 2^{2k+4}$
. Is
$n\leq 2^{2k+4}$
. Is
![]() $p := 2^{2k+4}-n < {\sf lh}(\sigma (k))$
?
$p := 2^{2k+4}-n < {\sf lh}(\sigma (k))$
?
If
yes,
set
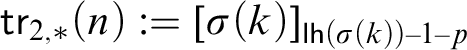 $\mathsf {tr}_{2,\ast }(n) := [\sigma (k)]_{{\sf lh}(\sigma (k)) -1 -p}$
.
$\mathsf {tr}_{2,\ast }(n) := [\sigma (k)]_{{\sf lh}(\sigma (k)) -1 -p}$
.
If no, take
 $$ \begin{align*} m := n - \sum_{i=0}^{k-1}{\sf lh}(\sigma(i)). \end{align*} $$
$$ \begin{align*} m := n - \sum_{i=0}^{k-1}{\sf lh}(\sigma(i)). \end{align*} $$
Set
![]() $\mathsf {tr}_{2,\ast }(n) := {\sf gn}_{\ast }(\widehat {m})$
.
$\mathsf {tr}_{2,\ast }(n) := {\sf gn}_{\ast }(\widehat {m})$
.
It is left to the reader to verify that this computation really defines the function
![]() $\mathsf {tr}_{2,\ast }$
. Note that when computing
$\mathsf {tr}_{2,\ast }$
. Note that when computing
![]() $\mathsf {tr}_{2,\ast }(n)$
, we only resort to values of
$\mathsf {tr}_{2,\ast }(n)$
, we only resort to values of
![]() $\mathsf {tr}_{2,\ast }$
for arguments smaller than n, since
$\mathsf {tr}_{2,\ast }$
for arguments smaller than n, since
![]() ${\mathfrak n}(k-1) \leq n$
. Moreover, let
${\mathfrak n}(k-1) \leq n$
. Moreover, let
![]() $\mathsf {B} \colon \omega \to \omega $
the elementary function given by
$\mathsf {B} \colon \omega \to \omega $
the elementary function given by
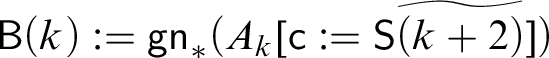 $\mathsf {B}(k) := \mathsf {gn}_{\ast }(A_k [{\sf c} := {\sf S}\widetilde {(k+2)}])$
. Note that
$\mathsf {B}(k) := \mathsf {gn}_{\ast }(A_k [{\sf c} := {\sf S}\widetilde {(k+2)}])$
. Note that
![]() $\mathsf {tr}_{2,\ast }(n)$
codes a filler expression of the form
$\mathsf {tr}_{2,\ast }(n)$
codes a filler expression of the form
![]() $\widehat {m}$
, or a sub-expression of
$\widehat {m}$
, or a sub-expression of
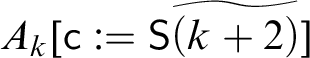 $A_k [{\sf c} := {\sf S}\widetilde {(k+2)}]$
. Since in each stage k, there are less than
$A_k [{\sf c} := {\sf S}\widetilde {(k+2)}]$
. Since in each stage k, there are less than
![]() ${\mathfrak n}(k)$
-many fillers added, we obtain the estimate
${\mathfrak n}(k)$
-many fillers added, we obtain the estimate
 $\mathsf {tr}_{2,\ast }(n) \leq \max ({\sf gn}_{\ast }(\widehat {(k+1) \cdot {\mathfrak n}(k)},\mathsf {B}(k))$
. Hence, the employed recursion is limited. Since elementary functions are closed under limited course-of-values recursion, we conclude that
$\mathsf {tr}_{2,\ast }(n) \leq \max ({\sf gn}_{\ast }(\widehat {(k+1) \cdot {\mathfrak n}(k)},\mathsf {B}(k))$
. Hence, the employed recursion is limited. Since elementary functions are closed under limited course-of-values recursion, we conclude that
![]() $\mathsf {tr}_{2,\ast } \in \mathfrak {El}$
.
$\mathsf {tr}_{2,\ast } \in \mathfrak {El}$
.
In order to show that
![]() $\mathsf {tr}_{\ast ,2}$
is elementary, we use the fact that a function is elementary if (1) its graph is elementary and (2) it can be dominated by an elementary function. Since
$\mathsf {tr}_{\ast ,2}$
is elementary, we use the fact that a function is elementary if (1) its graph is elementary and (2) it can be dominated by an elementary function. Since
![]() $\mathsf {tr}_{2,\ast }$
is elementary, it is easy to check that the graph of
$\mathsf {tr}_{2,\ast }$
is elementary, it is easy to check that the graph of
![]() $\mathsf {tr}_{\ast ,2}$
is elementary. Hence, it is sufficient to show (2). Let
$\mathsf {tr}_{\ast ,2}$
is elementary. Hence, it is sufficient to show (2). Let
![]() $A_k \in \mathcal {L}$
. By Lemma 6.5,
$A_k \in \mathcal {L}$
. By Lemma 6.5,
![]() $A_k \in \Lambda _k$
. Hence,
$A_k \in \Lambda _k$
. Hence,
![]() $\mathsf {tr}_{\ast ,2}(k) < {\mathfrak n}(k)$
and we are done.□
$\mathsf {tr}_{\ast ,2}(k) < {\mathfrak n}(k)$
and we are done.□
It is easy to show that the elementary (or primitive recursive) relations and functions are invariant regarding numberings which are elementarily (or primitive recursively) intertranslatable.
Lemma 7.8. Let
![]() $\mathcal {C} \in \{\mathfrak {Po},\mathfrak {El},\mathfrak {Pr} \}$
. Let
$\mathcal {C} \in \{\mathfrak {Po},\mathfrak {El},\mathfrak {Pr} \}$
. Let
![]() $S_i$
be sets and let
$S_i$
be sets and let
![]() $\alpha _i, \beta _i \colon S_i \to \omega $
be injective functions such that the translation functions
$\alpha _i, \beta _i \colon S_i \to \omega $
be injective functions such that the translation functions
![]() $\alpha _i \circ \beta _i^{-1}$
and
$\alpha _i \circ \beta _i^{-1}$
and
![]() $\beta _i \circ \alpha _i^{-1}$
are in
$\beta _i \circ \alpha _i^{-1}$
are in
![]() $\mathcal {C}$
, for
$\mathcal {C}$
, for
![]() $i \in \{1, \ldots ,k\}$
and
$i \in \{1, \ldots ,k\}$
and
![]() $k \in \omega $
. For every
$k \in \omega $
. For every
![]() $R \subseteq S_1 \times \cdots \times S_k$
,
$R \subseteq S_1 \times \cdots \times S_k$
,
![]() $Q \subseteq S_{k+1}$
and function
$Q \subseteq S_{k+1}$
and function
![]() $f \colon R \to Q$
we then have:
$f \colon R \to Q$
we then have:
-
• The relation
is in $$ \begin{align*} \vec\alpha (R) := \{ \langle \alpha_1(s_1), \ldots, \alpha_k(s_k) \rangle \mid \langle s_1,\ldots,s_k \rangle \in R \} \end{align*} $$
$$ \begin{align*} \vec\alpha (R) := \{ \langle \alpha_1(s_1), \ldots, \alpha_k(s_k) \rangle \mid \langle s_1,\ldots,s_k \rangle \in R \} \end{align*} $$
 $\mathcal {C}$
iff
$\mathcal {C}$
iff
 $\vec \beta (R)$
is in
$\vec \beta (R)$
is in
 $\mathcal {C}$
.
$\mathcal {C}$
.
-
• The function
 $f_{\vec \alpha } \colon \vec \alpha (R) \to \omega $
given by is in
$f_{\vec \alpha } \colon \vec \alpha (R) \to \omega $
given by is in $$ \begin{align*} f_{\vec\alpha}(m_1, \ldots, m_k) := \alpha_{k+1}f(\alpha_1^{-1}(m_1), \ldots, \alpha_k^{-1}(m_k)) \end{align*} $$
$$ \begin{align*} f_{\vec\alpha}(m_1, \ldots, m_k) := \alpha_{k+1}f(\alpha_1^{-1}(m_1), \ldots, \alpha_k^{-1}(m_k)) \end{align*} $$
 $\mathcal {C}$
iff the function
$\mathcal {C}$
iff the function
 $f_{\vec \beta } \colon \vec \beta (R) \to \omega $
is in
$f_{\vec \beta } \colon \vec \beta (R) \to \omega $
is in
 $\mathcal {C}$
.
$\mathcal {C}$
.
We have seen in this section that
![]() $\mathfrak {Pr}$
-adequacy can be extracted as a necessary condition for reasonable numberings from the literature. Since
$\mathfrak {Pr}$
-adequacy can be extracted as a necessary condition for reasonable numberings from the literature. Since
![]() $\mathsf {gn}_{\ast }$
is
$\mathsf {gn}_{\ast }$
is
![]() $\mathfrak {El}$
-adequate we conclude from Lemmas 7.7 and 7.8 that the numberings
$\mathfrak {El}$
-adequate we conclude from Lemmas 7.7 and 7.8 that the numberings
![]() ${\sf gn}_0$
,
${\sf gn}_0$
,
![]() ${\sf gn}_1$
and
${\sf gn}_1$
and
![]() ${\sf gn}_2$
are
${\sf gn}_2$
are
![]() $\mathfrak {El}$
-adequate and, in particular,
$\mathfrak {El}$
-adequate and, in particular,
![]() $\mathfrak {Pr}$
-adequate. Thus, the computational constraint of
$\mathfrak {Pr}$
-adequate. Thus, the computational constraint of
![]() $\mathfrak {Pr}$
-adequacy (or
$\mathfrak {Pr}$
-adequacy (or
![]() $\mathfrak {El}$
-adequacy) is not sufficiently restrictive to deny these numberings the status of adequate formalisation choices.
$\mathfrak {El}$
-adequacy) is not sufficiently restrictive to deny these numberings the status of adequate formalisation choices.
Open Question 7.9 It remains open whether there are
![]() $\mathfrak {Po}$
-adequate versions of the constructions given in this paper. More specifically:
$\mathfrak {Po}$
-adequate versions of the constructions given in this paper. More specifically:
-
• Can we find
 $\mathfrak {Po}$
-adequate self-referential Gödel numberings that are monotonic?
$\mathfrak {Po}$
-adequate self-referential Gödel numberings that are monotonic? -
• Can we find
 $\mathfrak {Po}$
-adequate Gödel numberings which satisfy the Strong Diagonal Lemma 6.3 that are strongly monotonic?
$\mathfrak {Po}$
-adequate Gödel numberings which satisfy the Strong Diagonal Lemma 6.3 that are strongly monotonic?
8 Domination and Regularity
We have seen in Section 6 that strong monotonicity is not sufficient to rule out m-self-referential sentences formulated in
![]() $\mathcal {L}$
. This is due to the fact that the “fixed point” term t used in the proof of Lemma 6.3 is not an efficient numeral. Hence, conditions M3 and M4(
$\mathcal {L}$
. This is due to the fact that the “fixed point” term t used in the proof of Lemma 6.3 is not an efficient numeral. Hence, conditions M3 and M4(
![]() $\overline {\cdot }$
) do not force the value of t to be smaller than the code of the formula containing t.
$\overline {\cdot }$
) do not force the value of t to be smaller than the code of the formula containing t.
For the remainder of this section, let
![]() $\mathcal {L}$
,
$\mathcal {L}$
,
![]() $\mathcal {K}$
be fixed languages with
$\mathcal {K}$
be fixed languages with
![]() $\mathcal {L}^0 \subseteq \mathcal {K} \subseteq \mathcal {L}$
, as specified in Section 2.1. We introduce two related constraints on numberings of
$\mathcal {L}^0 \subseteq \mathcal {K} \subseteq \mathcal {L}$
, as specified in Section 2.1. We introduce two related constraints on numberings of
![]() $\mathcal {L}$
which prohibit the code of a closed
$\mathcal {L}$
which prohibit the code of a closed
![]() $\mathcal {K}$
-term to be smaller than its value. We will see that together with requiring monotonicity, these constraints, applied to
$\mathcal {K}$
-term to be smaller than its value. We will see that together with requiring monotonicity, these constraints, applied to
![]() $\mathcal {L}$
, rule out m-self-referential sentences formulated in
$\mathcal {L}$
, rule out m-self-referential sentences formulated in
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
8.1 Domination
We start by defining the constraint of domination.
Definition 8.1. Let
![]() $\xi $
be a numbering of
$\xi $
be a numbering of
![]() $\mathcal {L}$
. We say that
$\mathcal {L}$
. We say that
![]() $\xi $
is
$\xi $
is
![]() $\mathcal {K}$
-dominating, if it satisfies the following principle:
$\mathcal {K}$
-dominating, if it satisfies the following principle:
-
M5(
 $\mathcal {K}$
). For all
$\mathcal {K}$
). For all
 $t \in \mathsf {ClTerm}_{\mathcal {K}}$
whose value is in
$t \in \mathsf {ClTerm}_{\mathcal {K}}$
whose value is in
 $\xi (\mathcal {L})$
:
$\xi (\mathcal {L})$
:
 $\mathsf {ev}(t) \leq \xi ( t )$
.
$\mathsf {ev}(t) \leq \xi ( t )$
.
We say that
![]() $\xi $
is dominating, if it is
$\xi $
is dominating, if it is
![]() $\mathcal {L}$
-dominating.
$\mathcal {L}$
-dominating.
Monotonic dominating numberings are strongly monotonic. More precisely, M5(
![]() $\mathcal {K}$
) implies M4
$\mathcal {K}$
) implies M4
![]() $^{\ast }$
(
$^{\ast }$
(
![]() $\nu $
) for every numeral function
$\nu $
) for every numeral function
![]() $\nu $
for
$\nu $
for
![]() $\mathcal K$
(cf. Section 6):
$\mathcal K$
(cf. Section 6):
Corollary 8.2. Let
![]() $\nu $
be a numeral function for
$\nu $
be a numeral function for
![]() $\mathcal {K}$
and let
$\mathcal {K}$
and let
![]() $\xi $
be a numbering of
$\xi $
be a numbering of
![]() $\mathcal {L}$
. If
$\mathcal {L}$
. If
![]() $\xi $
satisfies M5
$\xi $
satisfies M5
![]() $(\mathcal {K})$
, then
$(\mathcal {K})$
, then
![]() $\xi $
satisfies M4
$\xi $
satisfies M4
![]() $^{\ast }(\nu )$
.
$^{\ast }(\nu )$
.
Proof. We have
![]() $n = \mathsf {ev}(\nu (n)) \leq \xi (\nu (n))$
for all
$n = \mathsf {ev}(\nu (n)) \leq \xi (\nu (n))$
for all
![]() $n \in \omega $
. Hence,
$n \in \omega $
. Hence,
![]() $\xi (A) \leq \xi ( \nu (\xi (A)) )$
for all
$\xi (A) \leq \xi ( \nu (\xi (A)) )$
for all
![]() $A \in \mathcal {L}$
.□
$A \in \mathcal {L}$
.□
We now show that when employing monotonic and
![]() $\mathcal {K}$
-dominating numberings, m-self-reference is not attainable in
$\mathcal {K}$
-dominating numberings, m-self-reference is not attainable in
![]() $\mathcal {K}$
. That is, taken together, these two constraints rule out the existence of strong fixed point terms in
$\mathcal {K}$
. That is, taken together, these two constraints rule out the existence of strong fixed point terms in
![]() $\mathcal K$
.
$\mathcal K$
.
Lemma 8.3. Let
![]() $\xi $
be a numbering of
$\xi $
be a numbering of
![]() $\mathcal {L}$
satisfying M3 and M5(
$\mathcal {L}$
satisfying M3 and M5(
![]() ${\mathcal {K}})$
. Then for all
${\mathcal {K}})$
. Then for all
![]() $\mathcal {L}$
-formulæ
$\mathcal {L}$
-formulæ
![]() $A(x)$
and closed
$A(x)$
and closed
![]() ${\mathcal {K}}$
-terms t,
${\mathcal {K}}$
-terms t,
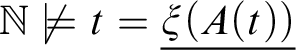 $\mathbb {N} \not \models t = \underline {\xi (A(t))}$
.
$\mathbb {N} \not \models t = \underline {\xi (A(t))}$
.
Proof. Assume that there exists an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $A(x)$
and a closed
$A(x)$
and a closed
![]() $\mathcal {K}$
-term t such that
$\mathcal {K}$
-term t such that
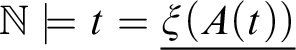 $\mathbb {N} \models t = \underline {\xi (A(t))}$
. Using M3 and M5(
$\mathbb {N} \models t = \underline {\xi (A(t))}$
. Using M3 and M5(
![]() ${\mathcal {K}}$
), we then derive the contradiction
${\mathcal {K}}$
), we then derive the contradiction
![]() $\mathsf {ev}(t) = \xi (A(t))> \xi (t) \geq \mathsf {ev}(t)$
.□
$\mathsf {ev}(t) = \xi (A(t))> \xi (t) \geq \mathsf {ev}(t)$
.□
Let
![]() $\xi $
be a standard numbering of
$\xi $
be a standard numbering of
![]() $\mathcal {L}^+$
, where
$\mathcal {L}^+$
, where
![]() $\mathcal {L}^+$
contains a term which represents the canonical strong diagonal function. That is,
$\mathcal {L}^+$
contains a term which represents the canonical strong diagonal function. That is,
![]() $\mathcal {L}^+$
represents the function which maps (the
$\mathcal {L}^+$
represents the function which maps (the
![]() $\xi $
-code of) an
$\xi $
-code of) an
![]() ${\mathcal {L}}^+$
-formula
${\mathcal {L}}^+$
-formula
![]() $A(x)$
with x free to (the
$A(x)$
with x free to (the
![]() $\xi $
-code of) its diagonalisation
$\xi $
-code of) its diagonalisation
 $A(\underline {\xi (A)})$
. As we have seen already, there exists an
$A(\underline {\xi (A)})$
. As we have seen already, there exists an
![]() $\mathcal {L}^+$
-formula
$\mathcal {L}^+$
-formula
![]() $A(x)$
and a term
$A(x)$
and a term
![]() $t \in {\mathcal {L}}^+$
such that
$t \in {\mathcal {L}}^+$
such that
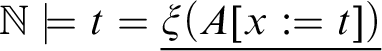 $\mathbb {N} \models t = \underline {\xi (A[ x := t])}$
(Lemma 1.1).
$\mathbb {N} \models t = \underline {\xi (A[ x := t])}$
(Lemma 1.1).
The reason to define the constraints of domination with respect to a sub-language of the domain of a numbering can be illustrated as follows. While
![]() $\xi $
cannot be dominating with respect to
$\xi $
cannot be dominating with respect to
![]() $\xi $
’s domain (namely,
$\xi $
’s domain (namely,
![]() $\mathcal {L}^+$
) by Lemma 8.3, it is possibly dominating with respect to the sub-language
$\mathcal {L}^+$
) by Lemma 8.3, it is possibly dominating with respect to the sub-language
![]() $\mathcal {L}^0$
(for instance in case that
$\mathcal {L}^0$
(for instance in case that
![]() $\xi $
is the length-first ordering).
$\xi $
is the length-first ordering).
However, as we will show in Section 8.2.2, there are reasonable numberings which even fail to be
![]() $\mathcal {L}^0$
-dominating. Moreover, there is a large class of standard numberings found in the literature which is not dominating with respect to languages which contain a function symbol for exponentiation or the smash function (see Section 8.2.3). These examples put considerable pressure on the view that domination is a necessary condition for reasonable choices of numberings. This constraint thus appears to be of no use to a philosophically adequate approach which aims to block the attainability of m-self-reference in arithmetic formulated in
$\mathcal {L}^0$
-dominating. Moreover, there is a large class of standard numberings found in the literature which is not dominating with respect to languages which contain a function symbol for exponentiation or the smash function (see Section 8.2.3). These examples put considerable pressure on the view that domination is a necessary condition for reasonable choices of numberings. This constraint thus appears to be of no use to a philosophically adequate approach which aims to block the attainability of m-self-reference in arithmetic formulated in
![]() $\mathcal {L}^0$
.
$\mathcal {L}^0$
.
Exactly the same remarks apply to the constraint of regularity, introduced in the next section.
8.2 Regularity
We now introduce another constraint on numberings, along the lines of a notion put forward in [Reference Heck13, p. 17].Footnote 14
Definition 8.4. Let
![]() $\xi $
be a numbering of
$\xi $
be a numbering of
![]() $\mathcal {L}$
. We say that
$\mathcal {L}$
. We say that
![]() $\xi $
is
$\xi $
is
![]() $\mathcal {K}$
-regular if
$\mathcal {K}$
-regular if
-
•
 $\xi (c) \geq c^{\mathbb {N}}$
for all constant symbols
$\xi (c) \geq c^{\mathbb {N}}$
for all constant symbols
 $c \in \mathcal {K}$
$c \in \mathcal {K}$
-
•
 $\xi (f(t_1,\ldots ,t_k))> f^{\mathbb {N}}(\xi (t_1),\ldots ,\xi (t_k))$
for all k-ary function symbols
$\xi (f(t_1,\ldots ,t_k))> f^{\mathbb {N}}(\xi (t_1),\ldots ,\xi (t_k))$
for all k-ary function symbols
 $f \in \mathcal {K}$
$f \in \mathcal {K}$
Moreover, we call
![]() $\xi $
regular, if it is
$\xi $
regular, if it is
![]() $\mathcal {L}$
-regular.
$\mathcal {L}$
-regular.
By induction we immediately get
Lemma 8.5. Let
![]() $\xi $
be a
$\xi $
be a
![]() $\mathcal {K}$
-regular numbering of
$\mathcal {K}$
-regular numbering of
![]() $\mathcal {L}$
. Then
$\mathcal {L}$
. Then
![]() $\xi $
satisfies M5
$\xi $
satisfies M5
![]() $(\mathcal {K})$
.
$(\mathcal {K})$
.
Thus,
![]() $\mathcal {K}$
-regular numberings are
$\mathcal {K}$
-regular numberings are
![]() $\mathcal {K}$
-dominating.
$\mathcal {K}$
-dominating.
8.2.1 Example of a regular numbering
A large class of standard numberings found in the literature are
![]() ${\mathcal {L}^0}$
-regular and hence in particular
${\mathcal {L}^0}$
-regular and hence in particular
![]() ${\mathcal {L}^0}$
-dominating. As an example, we show that the length-first numbering of
${\mathcal {L}^0}$
-dominating. As an example, we show that the length-first numbering of
![]() ${\mathcal {L}}$
is
${\mathcal {L}}$
is
![]() ${\mathcal {L}^0}$
-regular, where
${\mathcal {L}^0}$
-regular, where
![]() ${\mathcal L}$
is given in Polish notation (see Section 2.1). This follows as a corollary from a more general observation which has been suggested to us by Fedor Pakhomov.
${\mathcal L}$
is given in Polish notation (see Section 2.1). This follows as a corollary from a more general observation which has been suggested to us by Fedor Pakhomov.
Let S be a set of strings that is closed under the constructor operations
![]() $\dot {{\sf A}}$
and
$\dot {{\sf A}}$
and
![]() $\dot {{\sf M}}$
, given by
$\dot {{\sf M}}$
, given by
![]() $\langle \alpha ,\beta \rangle \mapsto {\sf A} \alpha \beta $
and
$\langle \alpha ,\beta \rangle \mapsto {\sf A} \alpha \beta $
and
![]() $\langle \alpha ,\beta \rangle \mapsto {\sf M} \alpha \beta $
respectively.
$\langle \alpha ,\beta \rangle \mapsto {\sf M} \alpha \beta $
respectively.
Let
![]() $\xi \colon S \to \omega $
be a numbering of S and let
$\xi \colon S \to \omega $
be a numbering of S and let
![]() $g \colon S^2 \to S$
be a binary operation on S. We call the function which maps
$g \colon S^2 \to S$
be a binary operation on S. We call the function which maps
![]() $\xi $
-codes
$\xi $
-codes
![]() $\langle m,n \rangle $
to
$\langle m,n \rangle $
to
![]() $\xi (g(\xi ^{-1}(m),\xi ^{-1}(n)))$
the
$\xi (g(\xi ^{-1}(m),\xi ^{-1}(n)))$
the
![]() $\xi $
-tracking function of g. As usual, we call a function
$\xi $
-tracking function of g. As usual, we call a function
![]() $f \colon \omega ^2 \to \omega $
monotonic, if
$f \colon \omega ^2 \to \omega $
monotonic, if
![]() $f(x_1, x_2) \leq f(y_1, y_2)$
for all
$f(x_1, x_2) \leq f(y_1, y_2)$
for all
![]() $x_1 \leq y_1$
and
$x_1 \leq y_1$
and
![]() $x_2 \leq y_2$
.
$x_2 \leq y_2$
.
Lemma 8.6 (Pakhomov)
Let
![]() $\xi \colon S \to \omega $
be a bijection such that the
$\xi \colon S \to \omega $
be a bijection such that the
![]() $\xi $
-tracking functions of
$\xi $
-tracking functions of
![]() $\dot {{\sf A}}$
and
$\dot {{\sf A}}$
and
![]() $\dot {{\sf M}}$
are monotonic. We have for all
$\dot {{\sf M}}$
are monotonic. We have for all
![]() $\alpha , \beta \in S$
:
$\alpha , \beta \in S$
:
Proof. We show the claim for
![]() ${\sf M} \alpha \beta $
. Let
${\sf M} \alpha \beta $
. Let
![]() $\alpha , \beta \in S$
. Since
$\alpha , \beta \in S$
. Since
![]() $\xi $
is bijective, there are
$\xi $
is bijective, there are
![]() $(\xi (\alpha )+1) \cdot (\xi (\beta )+1)$
-many pairs of expressions
$(\xi (\alpha )+1) \cdot (\xi (\beta )+1)$
-many pairs of expressions
![]() $\langle \alpha ',\beta ' \rangle $
such that
$\langle \alpha ',\beta ' \rangle $
such that
![]() $\xi (\alpha ') \leq \xi (\alpha )$
and
$\xi (\alpha ') \leq \xi (\alpha )$
and
![]() $\xi (\beta ') \leq \xi (\beta )$
. For each such pair
$\xi (\beta ') \leq \xi (\beta )$
. For each such pair
![]() $\langle \alpha ',\beta ' \rangle $
, we have
$\langle \alpha ',\beta ' \rangle $
, we have
![]() $\xi ({\sf M} \alpha ' \beta ') \leq \xi ({\sf M} \alpha \beta )$
, since the tracking function of
$\xi ({\sf M} \alpha ' \beta ') \leq \xi ({\sf M} \alpha \beta )$
, since the tracking function of
![]() $\dot {{\sf M}}$
is monotonic. Moreover, for any
$\dot {{\sf M}}$
is monotonic. Moreover, for any
![]() $\langle \alpha ',\beta ' \rangle \neq \langle \alpha '',\beta '' \rangle $
we have
$\langle \alpha ',\beta ' \rangle \neq \langle \alpha '',\beta '' \rangle $
we have
![]() $\xi ({\sf M} \alpha ' \beta ') \neq \xi ({\sf M} \alpha '' \beta '')$
by the injectivity of
$\xi ({\sf M} \alpha ' \beta ') \neq \xi ({\sf M} \alpha '' \beta '')$
by the injectivity of
![]() $\dot {{\sf M}}$
and
$\dot {{\sf M}}$
and
![]() $\xi $
. We thus conclude
$\xi $
. We thus conclude
In particular,
![]() $\xi (\alpha ) \cdot \xi (\beta ) < \xi ({\sf M} \alpha \beta )$
, if one of
$\xi (\alpha ) \cdot \xi (\beta ) < \xi ({\sf M} \alpha \beta )$
, if one of
![]() $\xi (\alpha )$
,
$\xi (\alpha )$
,
![]() $\xi (\beta )$
is
$\xi (\beta )$
is
![]() $> 0$
. Moreover, if both of
$> 0$
. Moreover, if both of
![]() $\xi (\alpha )$
,
$\xi (\alpha )$
,
![]() $\xi (\beta )$
are
$\xi (\beta )$
are
![]() $0$
, then, by injectivity,
$0$
, then, by injectivity,
![]() ${\sf M}\alpha \beta $
cannot be 0, so we have
${\sf M}\alpha \beta $
cannot be 0, so we have
![]() $\xi ({\sf M}\alpha \beta )>0 = \xi (\alpha )\cdot \xi (\beta )$
.□
$\xi ({\sf M}\alpha \beta )>0 = \xi (\alpha )\cdot \xi (\beta )$
.□
Let
![]() ${\mathcal L}$
be given in Polish notation and let
${\mathcal L}$
be given in Polish notation and let
![]() ${\mathcal A}$
be the alphabet of
${\mathcal A}$
be the alphabet of
![]() ${\mathcal L}$
. Let
${\mathcal L}$
. Let
![]() ${\mathfrak g}$
be the length-first numbering of
${\mathfrak g}$
be the length-first numbering of
![]() $\mathcal {A}^{\ast }$
. Note that since
$\mathcal {A}^{\ast }$
. Note that since
![]() ${\mathfrak g}$
is bijective and monotonic with respect to the sub-string relation, the assumptions of Lemma 8.6 are satisfied (for
${\mathfrak g}$
is bijective and monotonic with respect to the sub-string relation, the assumptions of Lemma 8.6 are satisfied (for
![]() $S := \mathcal {A}^{\ast }$
). It is then easy to derive the
$S := \mathcal {A}^{\ast }$
). It is then easy to derive the
![]() $\mathcal {L}^0$
-regularity of
$\mathcal {L}^0$
-regularity of
![]() ${\mathfrak g}$
.
${\mathfrak g}$
.
Corollary 8.7. The length-first numbering
![]() ${\mathfrak g}$
is
${\mathfrak g}$
is
![]() $\mathcal {L}^0$
-regular.
$\mathcal {L}^0$
-regular.
For any infinite subset Y of
![]() $\omega $
we define
$\omega $
we define
![]() ${\sf coll}_Y$
to be the unique order preserving bijection from Y to
${\sf coll}_Y$
to be the unique order preserving bijection from Y to
![]() $\omega $
.
$\omega $
.
Remark 8.8. Let
![]() $X := {\mathfrak g}({\mathcal L})$
. Consider the numbering
$X := {\mathfrak g}({\mathcal L})$
. Consider the numbering
![]() ${\mathfrak h} := {\sf coll}_X \circ {\mathfrak g}$
of
${\mathfrak h} := {\sf coll}_X \circ {\mathfrak g}$
of
![]() $\mathcal {L}$
. The numbering
$\mathcal {L}$
. The numbering
![]() ${\mathfrak h}$
can be seen as a length-first enumeration of the well-formed expressions in
${\mathfrak h}$
can be seen as a length-first enumeration of the well-formed expressions in
![]() $\mathcal {L}$
(as opposed to considering arbitrary strings of
$\mathcal {L}$
(as opposed to considering arbitrary strings of
![]() ${\mathcal A}$
). Arguably,
${\mathcal A}$
). Arguably,
![]() ${\mathfrak h}$
is a reasonable choice of a Gödel numbering.
${\mathfrak h}$
is a reasonable choice of a Gödel numbering.
Is
![]() ${{\mathfrak h}} \ \mathcal {L}^0$
-regular? Note that Lemma 8.6 cannot be applied to
${{\mathfrak h}} \ \mathcal {L}^0$
-regular? Note that Lemma 8.6 cannot be applied to
![]() ${\mathfrak h}$
. This is because its domain
${\mathfrak h}$
. This is because its domain
![]() $\mathcal {L}$
is not single-sorted as it contains both terms and formulæ. Hence,
$\mathcal {L}$
is not single-sorted as it contains both terms and formulæ. Hence,
![]() $\mathcal {L}$
is not closed under the constructor operations
$\mathcal {L}$
is not closed under the constructor operations
![]() $\dot {{\sf A}}$
and
$\dot {{\sf A}}$
and
![]() $\dot {{\sf M}}$
. However, we can use this lemma to show that the length-first enumeration of the closed-term fragment of
$\dot {{\sf M}}$
. However, we can use this lemma to show that the length-first enumeration of the closed-term fragment of
![]() $\mathcal {L}^0$
is
$\mathcal {L}^0$
is
![]() $\mathcal {L}^0$
-regular. Let
$\mathcal {L}^0$
-regular. Let
![]() $\mathcal {L}^{\circ }$
be given by
$\mathcal {L}^{\circ }$
be given by
-
•
 $t ::= {\sf 0} \mid {\sf S}t \mid {\sf A} t t \mid {\sf M} t t$
.
$t ::= {\sf 0} \mid {\sf S}t \mid {\sf A} t t \mid {\sf M} t t$
.
Let
![]() $X^{\circ } := {\mathfrak g}({\mathcal L}^{\circ })$
. We take
$X^{\circ } := {\mathfrak g}({\mathcal L}^{\circ })$
. We take
![]() ${\mathfrak h}^{\circ } := {\sf coll}_{X^{\circ }} \circ {\mathfrak g}$
to be the numbering of
${\mathfrak h}^{\circ } := {\sf coll}_{X^{\circ }} \circ {\mathfrak g}$
to be the numbering of
![]() $\mathcal {L}^{\circ }$
. Note
$\mathcal {L}^{\circ }$
. Note
![]() $\mathcal {L}^{\circ }$
is closed under both
$\mathcal {L}^{\circ }$
is closed under both
![]() $\dot {{\sf A}}$
and
$\dot {{\sf A}}$
and
![]() $\dot {{\sf M}}$
. Hence, we can conclude from Lemma 8.6 that
$\dot {{\sf M}}$
. Hence, we can conclude from Lemma 8.6 that
![]() ${\mathfrak h}^{\circ }$
is
${\mathfrak h}^{\circ }$
is
![]() $\mathcal {L}^0$
-regular.
$\mathcal {L}^0$
-regular.
8.2.2 Example of a non-regular numbering
We define a non-regular numbering of
![]() $\mathcal {L}^0$
, given in Polish notation (see Section 2.1).Footnote
15
Let
$\mathcal {L}^0$
, given in Polish notation (see Section 2.1).Footnote
15
Let
![]() $\mathcal {L}^{\star }$
denote the following extension of
$\mathcal {L}^{\star }$
denote the following extension of
![]() $\mathcal {L}^0$
:
$\mathcal {L}^0$
:
-
•
 $x::= {\sf v} \mid x'$
$x::= {\sf v} \mid x'$
-
•
 $t ::= {\sf 0} \mid x \mid {\sf S}t \mid {\sf A}tt \mid {\sf A}d \mid {\sf M}tt \mid {\sf M} d$
$t ::= {\sf 0} \mid x \mid {\sf S}t \mid {\sf A}tt \mid {\sf A}d \mid {\sf M}tt \mid {\sf M} d$
-
•
 $A ::= \bot \mid \top \mid {=}tt \mid {=}d \mid \neg A \mid \wedge A A \mid \wedge D \mid \vee A A \mid \vee D \mid {\to } A A \mid {\to } D \mid \forall x\,A \mid \exists x\, A$
$A ::= \bot \mid \top \mid {=}tt \mid {=}d \mid \neg A \mid \wedge A A \mid \wedge D \mid \vee A A \mid \vee D \mid {\to } A A \mid {\to } D \mid \forall x\,A \mid \exists x\, A$
-
•
 $d ::= \delta t$
$d ::= \delta t$
-
•
 $D ::= \Delta A$
$D ::= \Delta A$
The language
![]() $\mathcal {L}^{\star }$
can be seen to implement the sharing of certain sub-expressions. That is,
$\mathcal {L}^{\star }$
can be seen to implement the sharing of certain sub-expressions. That is,
![]() $\mathcal {L}^0$
-expressions of the form
$\mathcal {L}^0$
-expressions of the form
![]() $Bt t$
, for any binary constructor symbol B, are “contracted” to expressions of the form
$Bt t$
, for any binary constructor symbol B, are “contracted” to expressions of the form
![]() $B \delta t$
. This contraction and its reversal is performed by the translation functions
$B \delta t$
. This contraction and its reversal is performed by the translation functions
![]() $\mathfrak c \colon \mathcal {L}^0 \to \mathcal {L^{\star }}$
and
$\mathfrak c \colon \mathcal {L}^0 \to \mathcal {L^{\star }}$
and
![]() ${\mathfrak t} \colon \mathcal {L^{\star }} \to \mathcal {L}^0$
, defined recursively as follows: Both translations commute with all construction steps for t and A involving the zero-ary operations, the unary operations and the quantifiers. Moreover:
${\mathfrak t} \colon \mathcal {L^{\star }} \to \mathcal {L}^0$
, defined recursively as follows: Both translations commute with all construction steps for t and A involving the zero-ary operations, the unary operations and the quantifiers. Moreover:
-
•
 $\mathfrak c({\sf A} t u) := \begin {cases} {\sf A} \delta \mathfrak c(t) & \mathrm{if } t = u;\\ {\sf A} \mathfrak c(t) \mathfrak c(u) & \mathrm{if } t \neq u;\\ \end {cases}$
$\mathfrak c({\sf A} t u) := \begin {cases} {\sf A} \delta \mathfrak c(t) & \mathrm{if } t = u;\\ {\sf A} \mathfrak c(t) \mathfrak c(u) & \mathrm{if } t \neq u;\\ \end {cases}$
-
similarly, for M;
-
•
 $\mathfrak c({=} t u) := \begin {cases} {=} \delta \mathfrak c(t) & \mathrm{if } t = u;\\ {=} \mathfrak c(t) \mathfrak c(u) & \mathrm{if } t \neq u;\\ \end {cases}$
$\mathfrak c({=} t u) := \begin {cases} {=} \delta \mathfrak c(t) & \mathrm{if } t = u;\\ {=} \mathfrak c(t) \mathfrak c(u) & \mathrm{if } t \neq u;\\ \end {cases}$
-
•
 $\mathfrak c(\wedge AB) := \begin {cases} \wedge \Delta \mathfrak c(A) & \mathrm{if } A = B;\\ \wedge \mathfrak c(A) \mathfrak c(B) & \mathrm{if } A \neq B;\\ \end {cases}$
$\mathfrak c(\wedge AB) := \begin {cases} \wedge \Delta \mathfrak c(A) & \mathrm{if } A = B;\\ \wedge \mathfrak c(A) \mathfrak c(B) & \mathrm{if } A \neq B;\\ \end {cases}$
-
similarly, for
 $\vee $
and
$\vee $
and
 $\to $
.
$\to $
. -
•
 ${\mathfrak t}(\mathsf {A} \delta t) := \mathsf {A} {\mathfrak t}(t) {\mathfrak t} (t)$
;
${\mathfrak t}(\mathsf {A} \delta t) := \mathsf {A} {\mathfrak t}(t) {\mathfrak t} (t)$
; -
similarly, for M;
-
•
 ${\mathfrak t}({=} \delta t) := {=} {\mathfrak t}(t) {\mathfrak t} (t)$
;
${\mathfrak t}({=} \delta t) := {=} {\mathfrak t}(t) {\mathfrak t} (t)$
; -
•
 ${\mathfrak t}(\wedge \Delta A) := \wedge {\mathfrak t}(A) {\mathfrak t}(A)$
;
${\mathfrak t}(\wedge \Delta A) := \wedge {\mathfrak t}(A) {\mathfrak t}(A)$
; -
similarly for
 $\vee $
and
$\vee $
and
 $\to $
.
$\to $
.
The translation
![]() ${\mathfrak t}$
is well-defined. This follows from unique readability, which is proved in the lemma below.
${\mathfrak t}$
is well-defined. This follows from unique readability, which is proved in the lemma below.
Lemma 8.9.
![]() $\mathcal {L}^{\star }$
satisfies unique readability.
$\mathcal {L}^{\star }$
satisfies unique readability.
First Proof. Consider the language
![]() $\hat {{\mathcal L}}$
that consists of the arithmetical language extended with a new constant
$\hat {{\mathcal L}}$
that consists of the arithmetical language extended with a new constant
![]() $\delta $
and a new (zero-ary) proposition symbol
$\delta $
and a new (zero-ary) proposition symbol
![]() $\Delta $
. We prove by an easy induction that every syntactical string of
$\Delta $
. We prove by an easy induction that every syntactical string of
![]() ${\mathcal L}^{\star }$
is a syntactical string of
${\mathcal L}^{\star }$
is a syntactical string of
![]() $\hat {{\mathcal L}}$
. Now suppose an
$\hat {{\mathcal L}}$
. Now suppose an
![]() ${\mathcal L}^{\star }$
syntactical object has two readings. We consider e.g., the case where one of those readings is
${\mathcal L}^{\star }$
syntactical object has two readings. We consider e.g., the case where one of those readings is
![]() ${\sf M}\delta t$
. Clearly, the other reading can only be of the form
${\sf M}\delta t$
. Clearly, the other reading can only be of the form
![]() ${\sf M}\delta t$
since no
${\sf M}\delta t$
since no
![]() ${\mathcal L}^{\star }$
-term can begin with
${\mathcal L}^{\star }$
-term can begin with
![]() $\delta $
. Now consider the case where one reading is
$\delta $
. Now consider the case where one reading is
![]() ${\sf M}t_1t_2$
. The other reading must be of the form
${\sf M}t_1t_2$
. The other reading must be of the form
![]() ${\sf M}u_1u_2$
. We apply the embedding into
${\sf M}u_1u_2$
. We apply the embedding into
![]() $\hat {{\mathcal L}}$
and unique reading in
$\hat {{\mathcal L}}$
and unique reading in
![]() $\hat {{\mathcal L}}$
, to see that
$\hat {{\mathcal L}}$
, to see that
![]() $t_1=u_1$
and
$t_1=u_1$
and
![]() $t_2=u_2$
.□
$t_2=u_2$
.□
Second Proof. Consider the language
![]() $\breve {{\mathcal L}}$
that consists of the arithmetical language extended with new unary functions
$\breve {{\mathcal L}}$
that consists of the arithmetical language extended with new unary functions
![]() ${\sf A}_{\delta }$
and
${\sf A}_{\delta }$
and
![]() ${\sf M}_{\delta }$
, a new unary predicate symbol
${\sf M}_{\delta }$
, a new unary predicate symbol
![]() $=_{\delta }$
and new unary connectives
$=_{\delta }$
and new unary connectives
![]() $\wedge _{\Delta }$
,
$\wedge _{\Delta }$
,
![]() $\vee _{\Delta }$
and
$\vee _{\Delta }$
and
![]() $\to _{\Delta }$
. We map
$\to _{\Delta }$
. We map
![]() ${\mathcal L}^{\star }$
into
${\mathcal L}^{\star }$
into
![]() $\breve {{\mathcal L}}$
by the obvious mapping
$\breve {{\mathcal L}}$
by the obvious mapping
![]() ${\mathfrak d}$
that sends, e.g.,
${\mathfrak d}$
that sends, e.g.,
![]() ${\sf A}t_1t_2$
to
${\sf A}t_1t_2$
to
![]() ${\sf A}{\mathfrak d}(t_1) {\mathfrak d}(t_2)$
and
${\sf A}{\mathfrak d}(t_1) {\mathfrak d}(t_2)$
and
![]() ${\sf A}\delta t $
to
${\sf A}\delta t $
to
![]() ${\sf A}_{\delta } {\mathfrak d}(t)$
. It is easy to see that
${\sf A}_{\delta } {\mathfrak d}(t)$
. It is easy to see that
![]() ${\mathfrak d}$
is well-defined (since no
${\mathfrak d}$
is well-defined (since no
![]() ${\mathcal L}^{\star }$
-term can start with
${\mathcal L}^{\star }$
-term can start with
![]() $\delta $
and no
$\delta $
and no
![]() ${\mathcal L}^{\star }$
-formula can start with
${\mathcal L}^{\star }$
-formula can start with
![]() $\Delta $
) and injective.
$\Delta $
) and injective.
Now suppose an
![]() ${\mathcal L}^{\star }$
syntactical object has two readings. We consider, e.g., the case where one of those readings is
${\mathcal L}^{\star }$
syntactical object has two readings. We consider, e.g., the case where one of those readings is
![]() ${\sf M}\delta t$
. Clearly, the other reading can only be of the form
${\sf M}\delta t$
. Clearly, the other reading can only be of the form
![]() ${\sf M}\delta t$
since no
${\sf M}\delta t$
since no
![]() ${\mathcal L}^{\star }$
-term can begin with
${\mathcal L}^{\star }$
-term can begin with
![]() $\delta $
. Now consider the case where one reading is
$\delta $
. Now consider the case where one reading is
![]() ${\sf M}t_1t_2$
. The other reading must be of the form
${\sf M}t_1t_2$
. The other reading must be of the form
![]() ${\sf M}u_1u_2$
. We apply the embedding
${\sf M}u_1u_2$
. We apply the embedding
![]() ${\mathfrak d}$
into
${\mathfrak d}$
into
![]() $\hat {{\mathcal L}}$
and unique reading in
$\hat {{\mathcal L}}$
and unique reading in
![]() $\hat {{\mathcal L}}$
, to see that
$\hat {{\mathcal L}}$
, to see that
![]() ${\mathfrak d}(t_1)={\mathfrak d}(u_1)$
and
${\mathfrak d}(t_1)={\mathfrak d}(u_1)$
and
![]() ${\mathfrak d}(t_2)={\mathfrak d}(u_2)$
. By the injectivity of
${\mathfrak d}(t_2)={\mathfrak d}(u_2)$
. By the injectivity of
![]() ${\mathfrak d}$
, we find
${\mathfrak d}$
, we find
![]() $t_1=u_1$
and
$t_1=u_1$
and
![]() $t_2=u_2$
.□
$t_2=u_2$
.□
Let
![]() ${\mathcal A}$
be the alphabet of
${\mathcal A}$
be the alphabet of
![]() ${\mathcal L}^{\star }$
with some fixed ordering. Let
${\mathcal L}^{\star }$
with some fixed ordering. Let
![]() $\mathfrak {g}$
be the length-first numbering of
$\mathfrak {g}$
be the length-first numbering of
![]() ${\mathcal A}^{\ast }$
. We define our numbering
${\mathcal A}^{\ast }$
. We define our numbering
![]() ${\sf gn}_3$
of
${\sf gn}_3$
of
![]() $\mathcal {L}^0$
by setting
$\mathcal {L}^0$
by setting
![]() ${\sf gn}_3(\varphi ) := \mathfrak {g}(\mathfrak c(\varphi ))$
. Clearly,
${\sf gn}_3(\varphi ) := \mathfrak {g}(\mathfrak c(\varphi ))$
. Clearly,
![]() ${\sf gn}_3$
is injective, effective and (strongly) monotonic. We show that
${\sf gn}_3$
is injective, effective and (strongly) monotonic. We show that
![]() ${\sf gn}_3$
is not regular.
${\sf gn}_3$
is not regular.
Theorem 8.10.
![]() ${\sf gn}_3$
is not regular.
${\sf gn}_3$
is not regular.
Proof. Since the size of
![]() ${\mathcal A}$
is 17, by Lemma 2.3 we have for each
${\mathcal A}$
is 17, by Lemma 2.3 we have for each
![]() $\alpha \in {\mathcal A}^{\ast }$
$\alpha \in {\mathcal A}^{\ast }$
 $$ \begin{align*} \frac{17^{|\alpha|}-1}{16} \leq \mathfrak{g}(\alpha) < \frac{17^{|\alpha|+1}-1}{16}. \end{align*} $$
$$ \begin{align*} \frac{17^{|\alpha|}-1}{16} \leq \mathfrak{g}(\alpha) < \frac{17^{|\alpha|+1}-1}{16}. \end{align*} $$
Hence,
-
•
 ${\sf gn}_3(\underline {n}) = \mathfrak {g}(\underline {n}) \geq \frac {17^{n+1}-1}{16}$
and
${\sf gn}_3(\underline {n}) = \mathfrak {g}(\underline {n}) \geq \frac {17^{n+1}-1}{16}$
and -
•
 ${\sf gn}_3(\mathsf {M}\underline {n} \, \underline {n}) = \mathfrak {g}(\mathsf {M} \delta \underline {n}) < \frac {17^{n+4}-1}{16}$
.
${\sf gn}_3(\mathsf {M}\underline {n} \, \underline {n}) = \mathfrak {g}(\mathsf {M} \delta \underline {n}) < \frac {17^{n+4}-1}{16}$
.
But then, for all
![]() $n> 4$
,
$n> 4$
,
 $$ \begin{align*} {\sf gn}_3(\underline{n}) \cdot {\sf gn}_3(\underline{n}) & \geq \left(\frac{17^{n+1}-1}{16}\right)^{2}\\ & \geq \left(\frac{17^{n}}{16}\right)^{2}\\ & \geq \frac{17^{2n-1}}{16}\\ & \geq \frac{17^{n+4}-1}{16}\\ &> {\sf gn}_3(\mathsf{M}\underline{n} \, \underline{n}). \\[-32pt]\end{align*} $$
$$ \begin{align*} {\sf gn}_3(\underline{n}) \cdot {\sf gn}_3(\underline{n}) & \geq \left(\frac{17^{n+1}-1}{16}\right)^{2}\\ & \geq \left(\frac{17^{n}}{16}\right)^{2}\\ & \geq \frac{17^{2n-1}}{16}\\ & \geq \frac{17^{n+4}-1}{16}\\ &> {\sf gn}_3(\mathsf{M}\underline{n} \, \underline{n}). \\[-32pt]\end{align*} $$
□
We note that the computation in the above proof does not depend on the specific size of the alphabet, here represented by the numbers
![]() $17$
and
$17$
and
![]() $16=17-1$
. It works as long as the alphabet has at least two symbols. So, certainly, it works for all extensions for
$16=17-1$
. It works as long as the alphabet has at least two symbols. So, certainly, it works for all extensions for
![]() $\mathcal {L}^0$
.
$\mathcal {L}^0$
.
Remark 8.11. The present example of a non-regular Gödel numbering touches lightly upon a theme that we do not discuss in this paper: Gödel numberings based on alternative notions of syntax. Our treatment is mainly inspired by string approaches and algebraic approaches. In our example we look at sharing in the narrowest possible sense, but there are more principled and more encompassing approaches to sharing involving directed acyclic graphs and the like.
Similarly, there are different approaches to variables like de Bruijn notations and the Peirce–Quine linking notation. In Peirce diagrams and in the clause-set notation, we abstract away from the order of finite conjunctions. Etcetera.
We think that
![]() ${\sf gn}_3$
is a perfectly reasonable Gödel numbering. We strengthen this intuition by showing that
${\sf gn}_3$
is a perfectly reasonable Gödel numbering. We strengthen this intuition by showing that
![]() ${\sf gn}_3$
has good properties. Of course, even with the insights below, one may still have doubts about the naturality of
${\sf gn}_3$
has good properties. Of course, even with the insights below, one may still have doubts about the naturality of
![]() ${\sf gn}_3$
. Taking for a moment the standpoint of such a skeptic, one could say that we show how not to argue against
${\sf gn}_3$
. Taking for a moment the standpoint of such a skeptic, one could say that we show how not to argue against
![]() ${\sf gn}_3$
.
${\sf gn}_3$
.
Theorem 8.12.
![]() ${\sf gn}_3$
is monotonic. Moreover, it is strongly monotonic w.r.t. standard and efficient numerals.
${\sf gn}_3$
is monotonic. Moreover, it is strongly monotonic w.r.t. standard and efficient numerals.
Proof. We note that
![]() $\mathfrak c$
preserves direct sub-expressions, in other words, if
$\mathfrak c$
preserves direct sub-expressions, in other words, if
![]() $\tau $
is a direct sub-expression of
$\tau $
is a direct sub-expression of
![]() $\rho $
, then
$\rho $
, then
![]() $\mathfrak {c}(\tau )$
is a direct sub-expression of
$\mathfrak {c}(\tau )$
is a direct sub-expression of
![]() $\mathfrak c(\rho )$
. It follows that
$\mathfrak c(\rho )$
. It follows that
![]() $\mathfrak c$
preserves sub-expressions. Since
$\mathfrak c$
preserves sub-expressions. Since
![]() ${\mathfrak g}$
is monotonic, we may conclude that
${\mathfrak g}$
is monotonic, we may conclude that
![]() ${\sf gn}_3 = {\mathfrak g} \circ \mathfrak c$
is also monotonic. Moreover, it is easy to see that
${\sf gn}_3 = {\mathfrak g} \circ \mathfrak c$
is also monotonic. Moreover, it is easy to see that
![]() $\mathfrak c$
transforms standard numerals and efficient numerals identically. Hence,
$\mathfrak c$
transforms standard numerals and efficient numerals identically. Hence,
![]() ${\sf gn}_3$
inherits strong monotonicity both with respect to standard numerals and to efficient numerals from
${\sf gn}_3$
inherits strong monotonicity both with respect to standard numerals and to efficient numerals from
![]() ${\mathfrak g}$
.□
${\mathfrak g}$
.□
Remark 8.13. We can easily adapt the numerals introduced in Section 6.2 to the present situation in order to obtain numerals for which strong monotonicity fails w.r.t.
![]() ${\sf gn}_3$
. The numeral function on
${\sf gn}_3$
. The numeral function on
![]() $\mathcal {L}^0$
would look as follows.
$\mathcal {L}^0$
would look as follows.
-
i.
 ${\sf pd}^{\star }(0) := {\sf 0}$
and
${\sf pd}^{\star }(0) := {\sf 0}$
and
 ${\sf pd}^{\star }(1) := {\sf S}{\sf 0}$
.
${\sf pd}^{\star }(1) := {\sf S}{\sf 0}$
. -
ii. Suppose
 $n> 1$
, and n is not a power of a prime. Let p be the smallest prime that divides n. Say
$n> 1$
, and n is not a power of a prime. Let p be the smallest prime that divides n. Say
 $n = p^i\cdot m$
, were p does not divide m and
$n = p^i\cdot m$
, were p does not divide m and
 $i>0$
. Then
$i>0$
. Then
 ${\sf pd}^{\star }(n) := \times {\sf pd}^{\star }(p^i){\sf pd}^{\star }(m)$
.
${\sf pd}^{\star }(n) := \times {\sf pd}^{\star }(p^i){\sf pd}^{\star }(m)$
. -
iii. Suppose
 $n = p^i$
, where p is prime and
$n = p^i$
, where p is prime and
 $i>0$
. We take
$i>0$
. We take
 ${\sf pd}^{\star }(p) := \underline p$
. In case
${\sf pd}^{\star }(p) := \underline p$
. In case
 $i = 2k$
, for
$i = 2k$
, for
 $k>0$
, we set
$k>0$
, we set
 ${\sf pd}^{\star }(n) := \times {\sf pd}^{\star }(p^k){\sf pd}^{\star }(p^k)$
. In case
${\sf pd}^{\star }(n) := \times {\sf pd}^{\star }(p^k){\sf pd}^{\star }(p^k)$
. In case
 $i = 2k+1$
, for
$i = 2k+1$
, for
 $k>0$
, we set
$k>0$
, we set
 ${\sf pd}^{\star }(n) := \times \underline p {\times } {\sf pd}^{\star }(p^k){\sf pd}^{\star }(p^k)$
.
${\sf pd}^{\star }(n) := \times \underline p {\times } {\sf pd}^{\star }(p^k){\sf pd}^{\star }(p^k)$
.
It is easy to see that
![]() ${\sf pd}^{\circ } := \mathfrak c \circ {\sf pd}^{\star }$
behaves like
${\sf pd}^{\circ } := \mathfrak c \circ {\sf pd}^{\star }$
behaves like
![]() $\mathsf {pd}$
from Example 6.2 with
$\mathsf {pd}$
from Example 6.2 with
![]() ${\sf M}\delta $
in the role of
${\sf M}\delta $
in the role of
![]() $\mathsf {Q}$
. It follows that
$\mathsf {Q}$
. It follows that
 ${\sf gn}_3(2^{2^n})$
grows exponentially in n.
${\sf gn}_3(2^{2^n})$
grows exponentially in n.
8.2.3 Smash and exponentiation
Let
![]() $\#$
be a binary function symbol with Nelson’s Reference Nelson[20] smash function, given by
$\#$
be a binary function symbol with Nelson’s Reference Nelson[20] smash function, given by
![]() $(m,n) \mapsto 2^{|m| \cdot |n|}$
, as its intended interpretation. Let
$(m,n) \mapsto 2^{|m| \cdot |n|}$
, as its intended interpretation. Let
![]() ${\sf exp}$
be a unary function symbol for exponentiation. We set
${\sf exp}$
be a unary function symbol for exponentiation. We set
![]() $\mathcal {L}^{\#} := \mathcal {L}^0 \cup \{ \# \}$
and
$\mathcal {L}^{\#} := \mathcal {L}^0 \cup \{ \# \}$
and
![]() $\mathcal {L^{\sf exp}} := \mathcal {L}^0 \cup \{ {\sf exp} \}$
. We now show that there are standard numberings found in the literature which are neither
$\mathcal {L^{\sf exp}} := \mathcal {L}^0 \cup \{ {\sf exp} \}$
. We now show that there are standard numberings found in the literature which are neither
![]() $\mathcal {L}^{\#}$
-regular nor
$\mathcal {L}^{\#}$
-regular nor
![]() ${\mathcal {L}}^{\mathsf {exp}}$
-regular.
${\mathcal {L}}^{\mathsf {exp}}$
-regular.
Let
![]() $\xi $
be a numbering such that there exists a polynomial P with
$\xi $
be a numbering such that there exists a polynomial P with
 $$ \begin{align} \xi(A) < 2^{P(|A|)} \text{ for all } A. \end{align} $$
$$ \begin{align} \xi(A) < 2^{P(|A|)} \text{ for all } A. \end{align} $$
For instance, [Reference Buss2, Reference Buss3] contain numberings of
![]() $\mathcal {L}^{\#}$
with this property. Moreover, length-first numberings, such as our numbering
$\mathcal {L}^{\#}$
with this property. Moreover, length-first numberings, such as our numbering
![]() ${\mathfrak g}$
, satisfy (*). To see this, let
${\mathfrak g}$
, satisfy (*). To see this, let
![]() ${\mathfrak g}$
be a length-first numbering over an alphabet with size
${\mathfrak g}$
be a length-first numbering over an alphabet with size
![]() $N> 1$
. Consider any
$N> 1$
. Consider any
![]() $m \in \omega $
such that
$m \in \omega $
such that
![]() $N \leq 2^m$
. By Lemma 2.3 we find, for all A:
$N \leq 2^m$
. By Lemma 2.3 we find, for all A:
 $$ \begin{align*} {\mathfrak g}(A) < \frac{N^{|A|+1}-1}{N-1} < N^{|A|+1} \leq (2^m)^{|A|+1} = 2^{m \cdot |A|+m}. \end{align*} $$
$$ \begin{align*} {\mathfrak g}(A) < \frac{N^{|A|+1}-1}{N-1} < N^{|A|+1} \leq (2^m)^{|A|+1} = 2^{m \cdot |A|+m}. \end{align*} $$
We now show that any numbering
![]() $\xi $
satisfying (
$\xi $
satisfying (
![]() $\ast $
) is neither
$\ast $
) is neither
![]() $\mathcal {L}^{\#}$
-regular, nor
$\mathcal {L}^{\#}$
-regular, nor
![]() $\mathcal {L}^{\mathsf {exp}}$
-regular.
$\mathcal {L}^{\mathsf {exp}}$
-regular.
Theorem 8.14.
![]() $\xi $
is not
$\xi $
is not
![]() $\mathcal {L}^{\#}$
-regular.
$\mathcal {L}^{\#}$
-regular.
Proof. We define:
-
•
 $\widehat 1 := ({\sf SS}{\sf 0} \mathbin {\#} {\sf SS}{\sf 0})$
and
$\widehat 1 := ({\sf SS}{\sf 0} \mathbin {\#} {\sf SS}{\sf 0})$
and -
•
 $\widehat {n+1} := ({\sf SS}{\sf 0} \mathbin {\#} \widehat {n})$
.
$\widehat {n+1} := ({\sf SS}{\sf 0} \mathbin {\#} \widehat {n})$
.
It is easy to check that
 ${\sf ev}(\widehat n ) = 2^{2^{n+1}}$
and
${\sf ev}(\widehat n ) = 2^{2^{n+1}}$
and
![]() $|\widehat n| = 6n+3$
. Since P is a polynomial there exists
$|\widehat n| = 6n+3$
. Since P is a polynomial there exists
![]() $n \in \omega $
such that
$n \in \omega $
such that
![]() $P(6n+3) < 2^{n+1}$
and hence
$P(6n+3) < 2^{n+1}$
and hence
 $$ \begin{align*} \xi(\widehat{n}) < 2^{P(6n+3)} < 2^{2^{n+1}} = {\sf ev}(\widehat n ). \end{align*} $$
$$ \begin{align*} \xi(\widehat{n}) < 2^{P(6n+3)} < 2^{2^{n+1}} = {\sf ev}(\widehat n ). \end{align*} $$
Thus by, Lemma 8.5,
![]() $\xi $
is not
$\xi $
is not
![]() $\mathcal {L}^{\#}$
-regular.□
$\mathcal {L}^{\#}$
-regular.□
Theorem 8.15.
![]() $\xi $
is not
$\xi $
is not
![]() $\mathcal {L}^{\mathsf {exp}}$
-regular.
$\mathcal {L}^{\mathsf {exp}}$
-regular.
Proof. We define:
-
•
 and
and -
•
 .
.
We then have
and
.Footnote
16
Since P is a polynomial there exists
![]() $n \in \omega $
such that
$n \in \omega $
such that

Thus, by Lemma 8.5,
![]() $\xi $
is not
$\xi $
is not
![]() $\mathcal {L}^{\mathsf {exp}}$
-regular.□
$\mathcal {L}^{\mathsf {exp}}$
-regular.□
9 Type-free Truth Theories
Building on work by Heck Reference Heck[13] and Schindler Reference Schindler[25], we now apply the results obtained in this paper to the study of type-free axiomatic truth theories. More specifically, we show that the consistency of certain type-free truth theories depends on the employed formalisation choices. Consider for instance the following two important principles of truth:Footnote 17
-
NOT: The negation of a sentence A is true iff A is not true;
-
DISQ: A sentence of the form
 ${\ulcorner t\ \mathrm{ is\ true} \urcorner }$
is true iff t denotes a true sentence.
${\ulcorner t\ \mathrm{ is\ true} \urcorner }$
is true iff t denotes a true sentence.
Taken together, these principles can intuitively be shown to be inconsistent. In order to show this, consider the Liar sentence
-
 $(L)$
: L is not true.
$(L)$
: L is not true.
Since L is the sentence “L is not true”, L is true iff “L is not true” is true. By (NOT), “L is not true” is true iff “L is true” is not true. By (DISQ), “L is true” is not true iff, L is not true. Hence, L is true iff L is not true. Contradiction (see [Reference Heck13, p. 12]).
Using a similar argument, we can intuitively also show the inconsistency of the following truth principle:
-
NDISQ: A sentence of the form
 ${\ulcorner t\ \mathrm{ is\ not\ true} \urcorner }$
is true iff t denotes a sentence which is not true.
${\ulcorner t\ \mathrm{ is\ not\ true} \urcorner }$
is true iff t denotes a sentence which is not true.
Following Heck Reference Heck[13] and Schindler Reference Schindler[25] we ask in which arithmetical framework this informal reasoning can be captured. Let
![]() $\mathcal {L}$
be any primitive recursive extension of
$\mathcal {L}$
be any primitive recursive extension of
![]() ${\mathcal {L}^0}$
, i.e., the result of adding function symbols for certain primitive recursive functions to
${\mathcal {L}^0}$
, i.e., the result of adding function symbols for certain primitive recursive functions to
![]() ${\mathcal {L}^0}$
. We set
${\mathcal {L}^0}$
. We set
![]() $\mathcal {L}_{\mathsf {T}} := \mathcal {L} \cup \{ \mathsf {T} \}$
, where
$\mathcal {L}_{\mathsf {T}} := \mathcal {L} \cup \{ \mathsf {T} \}$
, where
![]() $\mathsf {T}$
is a new unary predicate symbol. The theory
$\mathsf {T}$
is a new unary predicate symbol. The theory
![]() $\mathsf {R}_{{\mathcal {L}}}$
serves as a (weak) syntax theory in the formalisation of informal truth principles. Let moreover
$\mathsf {R}_{{\mathcal {L}}}$
serves as a (weak) syntax theory in the formalisation of informal truth principles. Let moreover
![]() $\nu $
be a numeral function for
$\nu $
be a numeral function for
![]() $\mathcal {L}$
and let
$\mathcal {L}$
and let
![]() $\xi $
be a numbering of
$\xi $
be a numbering of
![]() $\mathcal {L}_{\mathsf {T}}$
. We now consider the following arithmetical formalisations of (NOT), (DISQ) and (NDISQ):
$\mathcal {L}_{\mathsf {T}}$
. We now consider the following arithmetical formalisations of (NOT), (DISQ) and (NDISQ):
 $$ \begin{align*} &\textbf{Not}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\neg A))) \leftrightarrow \neg \mathsf{T}(\nu(\xi(A))); \\ &\textbf{Disq}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\mathsf{T}(t)))) \leftrightarrow \mathsf{T}(t); \\ &\textbf{Disq}^{\ast}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\mathsf{T}(\nu(\xi(A)))))) \leftrightarrow \mathsf{T}(\nu(\xi(A))); \\ &\textbf{NDisq}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\neg \mathsf{T}(t)))) \leftrightarrow \neg \mathsf{T}(t); \\ &\textbf{NDisq}^{\ast}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\neg \mathsf{T}(\nu(\xi(A)))))) \leftrightarrow \neg \mathsf{T}(\nu(\xi(A))); \end{align*} $$
$$ \begin{align*} &\textbf{Not}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\neg A))) \leftrightarrow \neg \mathsf{T}(\nu(\xi(A))); \\ &\textbf{Disq}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\mathsf{T}(t)))) \leftrightarrow \mathsf{T}(t); \\ &\textbf{Disq}^{\ast}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\mathsf{T}(\nu(\xi(A)))))) \leftrightarrow \mathsf{T}(\nu(\xi(A))); \\ &\textbf{NDisq}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\neg \mathsf{T}(t)))) \leftrightarrow \neg \mathsf{T}(t); \\ &\textbf{NDisq}^{\ast}(\nu,\xi): \ \mathsf{T}(\nu(\xi(\neg \mathsf{T}(\nu(\xi(A)))))) \leftrightarrow \neg \mathsf{T}(\nu(\xi(A))); \end{align*} $$
where A is any
![]() $\mathcal {L}_{\mathsf {T}}$
-sentence and t is any closed
$\mathcal {L}_{\mathsf {T}}$
-sentence and t is any closed
![]() $\mathcal {L}$
-term. Roughly speaking, Disq
$\mathcal {L}$
-term. Roughly speaking, Disq
![]() $(\nu ,\xi )$
formalises (DISQ) by using all singular terms (of the given language) as names of sentences, while the formalisation Disq
$(\nu ,\xi )$
formalises (DISQ) by using all singular terms (of the given language) as names of sentences, while the formalisation Disq
![]() $^{\ast }(\nu ,\xi )$
only employs certain canonical names, namely,
$^{\ast }(\nu ,\xi )$
only employs certain canonical names, namely,
![]() $\nu $
-numerals. The same holds for NDisq
$\nu $
-numerals. The same holds for NDisq
![]() $(\nu ,\xi )$
and NDisq
$(\nu ,\xi )$
and NDisq
![]() $^{\ast }(\nu ,\xi )$
. For every formalisation choice
$^{\ast }(\nu ,\xi )$
. For every formalisation choice
![]() $\langle \mathcal {L}_{\mathsf {T}}, \nu , \xi \rangle $
we consider the formal truth theories
$\langle \mathcal {L}_{\mathsf {T}}, \nu , \xi \rangle $
we consider the formal truth theories
 $$ \begin{align*} \mathcal{S}(\mathcal{L}_{\mathsf{T}},\nu,\xi) & := \mathsf{R}_{{\mathcal{L}}_{\mathsf{T}}} + \text{Not}(\nu,\xi) + \text{Disq}(\nu,\xi);\\ \mathcal{S}^{\ast}(\mathcal{L}_{\mathsf{T}},\nu,\xi) & := \mathsf{R}_{{\mathcal{L}}_{\mathsf{T}}} + \text{Not}(\nu,\xi) + \text{Disq}^{\ast}(\nu,\xi);\\ \mathcal{T}(\mathcal{L}_{\mathsf{T}},\nu,\xi) & := \mathsf{R}_{{\mathcal{L}}_{\mathsf{T}}} + \text{NDisq}(\nu,\xi);\\ \mathcal{T}^{\ast}(\mathcal{L}_{\mathsf{T}},\nu,\xi) & := \mathsf{R}_{{\mathcal{L}}_{\mathsf{T}}} + \text{NDisq}^{\ast}(\nu,\xi). \end{align*} $$
$$ \begin{align*} \mathcal{S}(\mathcal{L}_{\mathsf{T}},\nu,\xi) & := \mathsf{R}_{{\mathcal{L}}_{\mathsf{T}}} + \text{Not}(\nu,\xi) + \text{Disq}(\nu,\xi);\\ \mathcal{S}^{\ast}(\mathcal{L}_{\mathsf{T}},\nu,\xi) & := \mathsf{R}_{{\mathcal{L}}_{\mathsf{T}}} + \text{Not}(\nu,\xi) + \text{Disq}^{\ast}(\nu,\xi);\\ \mathcal{T}(\mathcal{L}_{\mathsf{T}},\nu,\xi) & := \mathsf{R}_{{\mathcal{L}}_{\mathsf{T}}} + \text{NDisq}(\nu,\xi);\\ \mathcal{T}^{\ast}(\mathcal{L}_{\mathsf{T}},\nu,\xi) & := \mathsf{R}_{{\mathcal{L}}_{\mathsf{T}}} + \text{NDisq}^{\ast}(\nu,\xi). \end{align*} $$
In general, different formalisation choices
![]() $\langle \mathcal {L}_{\mathsf {T}}, \nu , \xi \rangle $
yield different theories.
$\langle \mathcal {L}_{\mathsf {T}}, \nu , \xi \rangle $
yield different theories.
We now address the question under which constraints on the underlying formalisation choices
![]() $\langle \mathcal {L}_{\mathsf {T}}, \nu , \xi \rangle $
the
$\langle \mathcal {L}_{\mathsf {T}}, \nu , \xi \rangle $
the
![]() $\mathcal {L}_{\mathsf {T}}$
-theories
$\mathcal {L}_{\mathsf {T}}$
-theories
![]() $\mathcal {S}(\mathcal {L}_{\mathsf {T}},\nu ,\xi )$
,
$\mathcal {S}(\mathcal {L}_{\mathsf {T}},\nu ,\xi )$
,
![]() $\mathcal {S}^{\ast }(\mathcal {L}_{\mathsf {T}},\nu ,\xi )$
,
$\mathcal {S}^{\ast }(\mathcal {L}_{\mathsf {T}},\nu ,\xi )$
,
![]() $\mathcal {T}(\mathcal {L}_{\mathsf {T}},\nu ,\xi )$
and
$\mathcal {T}(\mathcal {L}_{\mathsf {T}},\nu ,\xi )$
and
![]() $\mathcal {T}^{\ast }(\mathcal {L}_{\mathsf {T}},\nu ,\xi )$
are inconsistent. That is, under which conditions do these theories provide a faithful formalisation of the intuitive reasoning regarding (NOT) and (DISQ) as well as (NDISQ)?
$\mathcal {T}^{\ast }(\mathcal {L}_{\mathsf {T}},\nu ,\xi )$
are inconsistent. That is, under which conditions do these theories provide a faithful formalisation of the intuitive reasoning regarding (NOT) and (DISQ) as well as (NDISQ)?
The reader is reminded that
![]() ${\mathcal {L}}^+$
is a language which results from adding function symbols for primitive recursive functions to
${\mathcal {L}}^+$
is a language which results from adding function symbols for primitive recursive functions to
![]() $\mathcal {L}^0$
, such that
$\mathcal {L}^0$
, such that
![]() ${\mathcal {L}}^+$
contains a term which represents the canonical strong diagonal function. Building on work by Heck and Schindler, the following answer can be extracted from the results of this paper.
${\mathcal {L}}^+$
contains a term which represents the canonical strong diagonal function. Building on work by Heck and Schindler, the following answer can be extracted from the results of this paper.
Theorem 9.1. Let
![]() $\nu $
be given such that
$\nu $
be given such that
![]() $\nu = \underline {\cdot }$
or
$\nu = \underline {\cdot }$
or
![]() $\nu = \overline {\cdot }$
. Let
$\nu = \overline {\cdot }$
. Let
![]() $\gamma $
be an
$\gamma $
be an
![]() $\mathfrak {El}$
-adequate and strongly monotonic numbering of
$\mathfrak {El}$
-adequate and strongly monotonic numbering of
![]() ${\mathcal {L}}^+_{\mathsf {T}}$
for efficient numerals, which is
${\mathcal {L}}^+_{\mathsf {T}}$
for efficient numerals, which is
![]() $\mathcal {L}^0$
-regular. We then have
$\mathcal {L}^0$
-regular. We then have
 $$ \begin{align*} \begin{array}{ll@{\quad\qquad}ll} 1. &\mathcal{S}({\mathcal{L}^0_{\mathsf{T}}},\nu,{\sf gn}_2) \vdash \bot &5. &\mathcal{T}({\mathcal{L}^0_{\mathsf{T}}},\nu,{\sf gn}_2) \vdash \bot \\ 2. &\mathcal{S}^{\ast}({\mathcal{L}}^+_{\mathsf{T}},\overline{\cdot},{\sf gn}_0) \vdash \bot &6. &\mathcal{T}^{\ast}({\mathcal{L}}^+_{\mathsf{T}},\overline{\cdot},{\sf gn}_0) \vdash \bot \\ 3. &\mathcal{S}({\mathcal{L}^0_{\mathsf{T}}},\nu,\gamma) \not\vdash \bot &7. &\mathcal{T}({\mathcal{L}^0_{\mathsf{T}}},\nu,\gamma) \not\vdash \bot \\ 4. &\mathcal{S}^{\ast}({\mathcal{L}}^+_{\mathsf{T}},\nu,\gamma) \not\vdash \bot &8. &\mathcal{T}^{\ast}({\mathcal{L}}^+_{\mathsf{T}},\nu,\gamma) \not\vdash \bot \end{array} \\[-16pt]\end{align*} $$
$$ \begin{align*} \begin{array}{ll@{\quad\qquad}ll} 1. &\mathcal{S}({\mathcal{L}^0_{\mathsf{T}}},\nu,{\sf gn}_2) \vdash \bot &5. &\mathcal{T}({\mathcal{L}^0_{\mathsf{T}}},\nu,{\sf gn}_2) \vdash \bot \\ 2. &\mathcal{S}^{\ast}({\mathcal{L}}^+_{\mathsf{T}},\overline{\cdot},{\sf gn}_0) \vdash \bot &6. &\mathcal{T}^{\ast}({\mathcal{L}}^+_{\mathsf{T}},\overline{\cdot},{\sf gn}_0) \vdash \bot \\ 3. &\mathcal{S}({\mathcal{L}^0_{\mathsf{T}}},\nu,\gamma) \not\vdash \bot &7. &\mathcal{T}({\mathcal{L}^0_{\mathsf{T}}},\nu,\gamma) \not\vdash \bot \\ 4. &\mathcal{S}^{\ast}({\mathcal{L}}^+_{\mathsf{T}},\nu,\gamma) \not\vdash \bot &8. &\mathcal{T}^{\ast}({\mathcal{L}}^+_{\mathsf{T}},\nu,\gamma) \not\vdash \bot \end{array} \\[-16pt]\end{align*} $$
Proof. (3) follows from [Reference Heck13, theorem 1] and (7) is Proposition 2.2.6 in Reference Schindler[25]. (4) and (8) can be shown similarly, using the observation that
![]() $\nu $
-numerals are
$\nu $
-numerals are
![]() $\mathcal {L}^0$
-terms. See also [Reference Heck13, p. 13].
$\mathcal {L}^0$
-terms. See also [Reference Heck13, p. 13].
We prove (2). By Lemma 4.6 there exists
![]() $n \in \omega $
such that (Eq)
$n \in \omega $
such that (Eq)
![]() $n = {\sf gn}_0(\neg \mathsf {T}(\overline {n}))$
. We can then derive in
$n = {\sf gn}_0(\neg \mathsf {T}(\overline {n}))$
. We can then derive in
![]() $\mathcal {S}^{\ast }({\mathcal {L}}^+_{\mathsf {T}},\overline {\cdot },{\sf gn}_0)$
the following contradiction
$\mathcal {S}^{\ast }({\mathcal {L}}^+_{\mathsf {T}},\overline {\cdot },{\sf gn}_0)$
the following contradiction
 $$ \begin{align*} \mathsf{T}(\overline{n}) & \leftrightarrow \mathsf{T}(\overline{{\sf gn}_0(\neg \mathsf{T}(\overline{n}))}), \text{ using (Eq)}\\ & \leftrightarrow \neg \mathsf{T}(\overline{{\sf gn}_0(\mathsf{T}(\overline{n}))}), \text{ using Not} (\overline{\cdot},{\sf gn}_0)\\ & \leftrightarrow \neg \mathsf{T}(\overline{{\sf gn}_0(\mathsf{T}(\overline{{\sf gn}_0(\neg \mathsf{T}(\overline{n}))}))}), \text{ using (Eq)}\\ & \leftrightarrow \neg \mathsf{T}(\overline{{\sf gn}_0(\neg \mathsf{T}(\overline{n}))}), \text{ using Disq}^{\ast}(\overline{\cdot},{\sf gn}_0)\\ & \leftrightarrow \neg \mathsf{T}(\overline{n}), \text{ using (Eq)}. \\[-16pt]\end{align*} $$
$$ \begin{align*} \mathsf{T}(\overline{n}) & \leftrightarrow \mathsf{T}(\overline{{\sf gn}_0(\neg \mathsf{T}(\overline{n}))}), \text{ using (Eq)}\\ & \leftrightarrow \neg \mathsf{T}(\overline{{\sf gn}_0(\mathsf{T}(\overline{n}))}), \text{ using Not} (\overline{\cdot},{\sf gn}_0)\\ & \leftrightarrow \neg \mathsf{T}(\overline{{\sf gn}_0(\mathsf{T}(\overline{{\sf gn}_0(\neg \mathsf{T}(\overline{n}))}))}), \text{ using (Eq)}\\ & \leftrightarrow \neg \mathsf{T}(\overline{{\sf gn}_0(\neg \mathsf{T}(\overline{n}))}), \text{ using Disq}^{\ast}(\overline{\cdot},{\sf gn}_0)\\ & \leftrightarrow \neg \mathsf{T}(\overline{n}), \text{ using (Eq)}. \\[-16pt]\end{align*} $$
The proof of (6) proceeds similarly. (1) and (5) can be shown by applying Lemma 6.3.□
The results of the theorem can be summarised in the following table:

Thus, the conditions of
![]() $\mathfrak {El}$
-adequacy and monotonicity taken together are not restrictive enough to determine the consistency of
$\mathfrak {El}$
-adequacy and monotonicity taken together are not restrictive enough to determine the consistency of
![]() $\mathcal {S}^{\ast }({\mathcal {L}}^+_{\mathsf {T}},\overline {\cdot },\xi )$
and of
$\mathcal {S}^{\ast }({\mathcal {L}}^+_{\mathsf {T}},\overline {\cdot },\xi )$
and of
![]() $\mathcal {T}^{\ast }({\mathcal {L}}^+_{\mathsf {T}},\overline {\cdot },\xi )$
. Moreover, the conditions of
$\mathcal {T}^{\ast }({\mathcal {L}}^+_{\mathsf {T}},\overline {\cdot },\xi )$
. Moreover, the conditions of
![]() $\mathfrak {El}$
-adequacy and strong monotonicity for efficient numerals are together not restrictive enough to determine the consistency of
$\mathfrak {El}$
-adequacy and strong monotonicity for efficient numerals are together not restrictive enough to determine the consistency of
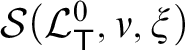 $\mathcal {S}(\mathcal {L}^0_{\mathsf {T}},\nu ,\xi )$
and of
$\mathcal {S}(\mathcal {L}^0_{\mathsf {T}},\nu ,\xi )$
and of
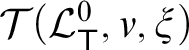 $\mathcal {T}(\mathcal {L}^0_{\mathsf {T}},\nu ,\xi )$
.
$\mathcal {T}(\mathcal {L}^0_{\mathsf {T}},\nu ,\xi )$
.
10 Summary and Perspectives
In our paper we have studied various requirements on formalisation choices, such as the Gödel numbering, under which m-self-reference is attainable in arithmetic. In particular, we have examined the admissibility of self-referential numberings, which provide immediate means to formalise m-self-reference. We have shown that monotonicity and
![]() $\mathfrak {El}$
-adequacy taken together do not exclude the self-referentiality of a numbering. While the constraint of strong monotonicity excludes the self-referentiality of numberings, we have shown that it does not block the attainability of m-self-reference in the basic language
$\mathfrak {El}$
-adequacy taken together do not exclude the self-referentiality of a numbering. While the constraint of strong monotonicity excludes the self-referentiality of numberings, we have shown that it does not block the attainability of m-self-reference in the basic language
![]() $\mathcal {L}^0$
. As a counterpoint, we have shown that the demand that the numbering is regular does indeed render m-self-reference in
$\mathcal {L}^0$
. As a counterpoint, we have shown that the demand that the numbering is regular does indeed render m-self-reference in
![]() $\mathcal {L}^0$
unattainable, but that, on the other hand, some completely decent numberings are non-regular. The obtained results show that the attainability of m-self-reference in
$\mathcal {L}^0$
unattainable, but that, on the other hand, some completely decent numberings are non-regular. The obtained results show that the attainability of m-self-reference in
![]() $\mathcal {L}^0$
is more sensitive to the underlying formalisation choices than widely believed. Finally, we have shown that this sensitivity also impinges on the formal study of certain principles of self-referential truth. Namely, whether or not certain axiomatic theories of self-referential truth are consistent is not determined by the constraints of
$\mathcal {L}^0$
is more sensitive to the underlying formalisation choices than widely believed. Finally, we have shown that this sensitivity also impinges on the formal study of certain principles of self-referential truth. Namely, whether or not certain axiomatic theories of self-referential truth are consistent is not determined by the constraints of
![]() $\mathfrak {El}$
-adequacy and (strong) monotonicity alone.
$\mathfrak {El}$
-adequacy and (strong) monotonicity alone.
In the paper we formulated some open questions that we repeat here.
-
A. Are there
 $\mathfrak {Po}$
-adequate numberings
$\mathfrak {Po}$
-adequate numberings
 $\xi $
for which
$\xi $
for which
 $\xi \circ (\underline \cdot )$
is p-time?
$\xi \circ (\underline \cdot )$
is p-time? -
B. Can we find
 $\mathfrak {Po}$
-adequate self-referential Gödel numberings that are monotonic?
$\mathfrak {Po}$
-adequate self-referential Gödel numberings that are monotonic? -
C. Can we find
 $\mathfrak {Po}$
-adequate Gödel numberings which satisfy the Strong Diagonal Lemma 6.3 that are strongly monotonic?
$\mathfrak {Po}$
-adequate Gödel numberings which satisfy the Strong Diagonal Lemma 6.3 that are strongly monotonic? -
D. Is the numbering
 ${\mathfrak h}$
(defined in Remark 8.8)
${\mathfrak h}$
(defined in Remark 8.8)
 $\mathcal {L}^0$
-regular?
$\mathcal {L}^0$
-regular?
Our paper is a primarily technical contribution providing data for philosophy. We have only gestured at philosophical motivations of the various constraints. We do believe that the motivations given in the literature for various constraints are extremely thin. However, we submit that this does not undermine the value of our contribution too much, since our work will still provide a philosopher who sets out to carefully argue for a constraint with an impression of what such a contraint does or does not mean. Moreover, both the self-referential numberings themselves and the study of various constraints on numberings have some technical interest entirely independent of the philosophical motivation of various constraints.
Acknowledgements
We thank Arnon Avron, Volker Halbach, Joel D. Hamkins, Fedor Pakhomov and two referees for valuable comments and suggestions. We would also like to thank the participants of Tel Aviv University’s Logic Seminar, of Carl Posy’s research seminar and of the workshop Ouroboros, Formal Criteria of Self-Reference in Mathematics and Philosophy. Balthasar Grabmayr’s work was partially supported by the Israeli Council for Higher Education (CHE).
A Appendix: An Alternative Construction of a Monotonic Self-Referential Numbering for Strings
We provide an alternative construction of a coding for strings which is self-referential for efficient numerals and monotonic with respect to the sub-expression relation. We believe that the inclusion of this construction is instructive, since in some sense it proceeds in a “bottom-up” and more direct fashion than the constructions given in Sections 4 and 5.
A.1 The length-first ordering and
 ${\sf gn}_4$
${\sf gn}_4$
Let
![]() ${\mathcal A}$
be the alphabet of the arithmetical language
${\mathcal A}$
be the alphabet of the arithmetical language
![]() $\mathcal {L}^0$
introduced in Subsection 2.1 and let
$\mathcal {L}^0$
introduced in Subsection 2.1 and let
![]() ${\mathcal A}^+$
be
${\mathcal A}^+$
be
![]() ${\mathcal A}$
extended with a fresh constant
${\mathcal A}$
extended with a fresh constant
![]() $\mathsf {c}$
and a fresh separator-symbol ;. We remind the reader of the fact that
$\mathsf {c}$
and a fresh separator-symbol ;. We remind the reader of the fact that
![]() ${\mathcal A}$
has 17 letters. Thus,
${\mathcal A}$
has 17 letters. Thus,
![]() ${\mathcal A}^+$
has 19 letters. We suppose some ordering of
${\mathcal A}^+$
has 19 letters. We suppose some ordering of
![]() ${\mathcal A}^+$
is given. Let
${\mathcal A}^+$
is given. Let
![]() ${\sf gn}_4$
be the length-first ordering of strings of
${\sf gn}_4$
be the length-first ordering of strings of
![]() ${\mathcal A}^+$
. Let
${\mathcal A}^+$
. Let
![]() $\alpha _n$
denote the string of
$\alpha _n$
denote the string of
![]() ${\mathcal A}^+$
with
${\mathcal A}^+$
with
![]() ${\sf gn}_4$
-code n. We write
${\sf gn}_4$
-code n. We write
![]() $|\alpha |$
for the length of
$|\alpha |$
for the length of
![]() $\alpha $
as before.
$\alpha $
as before.
We remind the reader that, by Lemma 2.3, we have
 $$ \begin{align*} \frac{19^{|\alpha|}-1}{18} \leq {\sf gn}_4(\alpha) < \frac{19^{|\alpha|+1}-1}{18}.\\[-16pt]\end{align*} $$
$$ \begin{align*} \frac{19^{|\alpha|}-1}{18} \leq {\sf gn}_4(\alpha) < \frac{19^{|\alpha|+1}-1}{18}.\\[-16pt]\end{align*} $$
It follows that
![]() $|\alpha | \leq {\sf gn}_4(\alpha )$
. Moreover, whenever
$|\alpha | \leq {\sf gn}_4(\alpha )$
. Moreover, whenever
![]() $|\alpha | < |\beta |$
, then
$|\alpha | < |\beta |$
, then
![]() ${\sf gn}_4(\alpha ) < {\sf gn}_4(\beta )$
.
${\sf gn}_4(\alpha ) < {\sf gn}_4(\beta )$
.
We define
![]() $\widetilde {n}$
as before and remind the reader that
$\widetilde {n}$
as before and remind the reader that
![]() ${\sf ev}(\widetilde {n} ) = 2^n -1$
and
${\sf ev}(\widetilde {n} ) = 2^n -1$
and
![]() $|\widetilde {n}| = 7n+1$
(see Lemma 3.6).
$|\widetilde {n}| = 7n+1$
(see Lemma 3.6).
A.2 On
 ${\sf gn}_5$
${\sf gn}_5$
We say that
![]() $\alpha $
is acceptable if it is of the form
$\alpha $
is acceptable if it is of the form
![]() $\gamma ;\delta $
, where
$\gamma ;\delta $
, where
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
are ;-free and where
$\delta $
are ;-free and where
![]() $\gamma $
is a sub-string of
$\gamma $
is a sub-string of
![]() $\delta $
. (Here we allow
$\delta $
. (Here we allow
![]() $\gamma = \delta $
.)
$\gamma = \delta $
.)
Suppose
![]() $\alpha _n=\gamma ;\delta $
is acceptable. We take
$\alpha _n=\gamma ;\delta $
is acceptable. We take
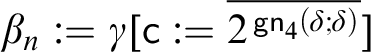 $\beta _n := \gamma [\mathsf {c}:= \overline {2^{\,{\sf gn}_4(\delta ;\delta )}}]$
. In other words, when
$\beta _n := \gamma [\mathsf {c}:= \overline {2^{\,{\sf gn}_4(\delta ;\delta )}}]$
. In other words, when
![]() $\delta ;\delta = \alpha _k$
, then
$\delta ;\delta = \alpha _k$
, then
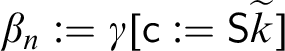 $\beta _n := \gamma [\mathsf {c}:= {\sf S}\widetilde k]$
. In all other cases we set
$\beta _n := \gamma [\mathsf {c}:= {\sf S}\widetilde k]$
. In all other cases we set
![]() $\beta _n$
to a don’t care value, say
$\beta _n$
to a don’t care value, say
![]() $\varepsilon $
, the empty string.
$\varepsilon $
, the empty string.
Lemma A.1.
![]() $(\beta _n)_{n\in \omega }$
enumerates the
$(\beta _n)_{n\in \omega }$
enumerates the
![]() ${\mathcal A}$
-strings.
${\mathcal A}$
-strings.
Proof. Clearly the
![]() $\beta _n$
neither contain ; nor
$\beta _n$
neither contain ; nor
![]() $\mathsf {c}$
, so they are
$\mathsf {c}$
, so they are
![]() $ {\mathcal A}$
-strings.
$ {\mathcal A}$
-strings.
Conversely, suppose
![]() $\theta $
is an
$\theta $
is an
![]() ${\mathcal A}$
-string. Let
${\mathcal A}$
-string. Let
![]() $\alpha _k = \theta ;\theta $
. Then, clearly,
$\alpha _k = \theta ;\theta $
. Then, clearly,
![]() $\beta _k = \theta $
.□
$\beta _k = \theta $
.□
We note that the enumeration
![]() $(\beta _n)_{n\in \omega }$
has repetitions. We proceed with a technical lemma.
$(\beta _n)_{n\in \omega }$
has repetitions. We proceed with a technical lemma.
Lemma A.2. Suppose
![]() $\gamma ;\delta $
is adequate and
$\gamma ;\delta $
is adequate and
![]() ${\sf gn}_4(\delta ;\delta )= n$
. Then,
${\sf gn}_4(\delta ;\delta )= n$
. Then,
![]() $|\widetilde {n}|> |\delta ;\delta | > |\gamma |$
, and, hence,
$|\widetilde {n}|> |\delta ;\delta | > |\gamma |$
, and, hence,
![]() ${\sf S}\widetilde {n}$
does not occur in
${\sf S}\widetilde {n}$
does not occur in
![]() $\gamma $
.
$\gamma $
.
Proof. We have:
 $$ \begin{align*} |\gamma| & < |\delta; \delta| \\ & \leq \frac{19^{|\delta;\delta|}-1}{18}\\ &\leq n \\ & < 7n+1\\ & = |\widetilde{n}|. \\[-33pt]\end{align*} $$
$$ \begin{align*} |\gamma| & < |\delta; \delta| \\ & \leq \frac{19^{|\delta;\delta|}-1}{18}\\ &\leq n \\ & < 7n+1\\ & = |\widetilde{n}|. \\[-33pt]\end{align*} $$
□
Lemma A.3. Consider acceptable
![]() $\zeta := \gamma ;\delta $
and
$\zeta := \gamma ;\delta $
and
![]() $\theta := \mu ;\eta $
. Let
$\theta := \mu ;\eta $
. Let
![]() ${\sf gn}_4(\delta ;\delta )=n$
and
${\sf gn}_4(\delta ;\delta )=n$
and
![]() ${\sf gn}_4(\eta ;\eta )=m$
. Suppose that
${\sf gn}_4(\eta ;\eta )=m$
. Suppose that
![]() $\mathsf {c}$
occurs both in
$\mathsf {c}$
occurs both in
![]() $\gamma $
and in
$\gamma $
and in
![]() $\mu $
and
$\mu $
and
![]() $\nu := \gamma [\mathsf {c} := {\sf S} \widetilde {n}] = \mu [\mathsf {c}:= {\sf S} \widetilde m]$
. Then,
$\nu := \gamma [\mathsf {c} := {\sf S} \widetilde {n}] = \mu [\mathsf {c}:= {\sf S} \widetilde m]$
. Then,
![]() $\zeta = \theta $
.
$\zeta = \theta $
.
Proof. We assume the conditions of the lemma. Note that n and m cannot be 0. In case
![]() $n=m$
, we see, by Lemmas 5.3 and A.2, that both
$n=m$
, we see, by Lemmas 5.3 and A.2, that both
![]() $\gamma $
and
$\gamma $
and
![]() $\epsilon $
are the result of replacing
$\epsilon $
are the result of replacing
![]() ${\sf S}\widetilde {n}$
in
${\sf S}\widetilde {n}$
in
![]() $\nu $
by
$\nu $
by
![]() $\mathsf {c}$
. It follows that
$\mathsf {c}$
. It follows that
![]() $\gamma = \mu $
. Trivially,
$\gamma = \mu $
. Trivially,
![]() $\delta = \eta $
. So,
$\delta = \eta $
. So,
![]() $\zeta =\theta $
.
$\zeta =\theta $
.
Suppose
![]() $m\neq n$
. This contradicts the fact that the largest term of the form
$m\neq n$
. This contradicts the fact that the largest term of the form
![]() ${\sf S}\widetilde {k}$
in
${\sf S}\widetilde {k}$
in
![]() $\nu = \gamma [\mathsf {c}:= {\sf S}\widetilde {n}]$
is
$\nu = \gamma [\mathsf {c}:= {\sf S}\widetilde {n}]$
is
![]() ${\sf S}\widetilde {n}$
and that the largest term of the form
${\sf S}\widetilde {n}$
and that the largest term of the form
![]() ${\sf S}\widetilde {k}$
in
${\sf S}\widetilde {k}$
in
![]() $\nu = \mu [\mathsf {c}:= {\sf S}\widetilde {m}]$
is
$\nu = \mu [\mathsf {c}:= {\sf S}\widetilde {m}]$
is
![]() ${\sf S}\widetilde m$
.□
${\sf S}\widetilde m$
.□
Lemma A.4. Consider any
![]() ${\mathcal A}$
-string
${\mathcal A}$
-string
![]() $\theta \neq \varepsilon $
. Let
$\theta \neq \varepsilon $
. Let
![]() $\alpha _m = \theta ;\theta $
. We have
$\alpha _m = \theta ;\theta $
. We have
![]() $\beta _m =\theta $
. Suppose
$\beta _m =\theta $
. Suppose
![]() $\alpha _n = \gamma ;\delta $
is acceptable and
$\alpha _n = \gamma ;\delta $
is acceptable and
![]() $\mathsf {c}$
occurs in
$\mathsf {c}$
occurs in
![]() $\gamma $
and
$\gamma $
and
![]() $\beta _n = \theta $
. Then
$\beta _n = \theta $
. Then
![]() $n<m$
.
$n<m$
.
Proof. The first claim is trivial. Suppose the conditions of the second claim. Let
![]() $\alpha _k = \delta ;\delta $
. We have, by Lemma A.2, that
$\alpha _k = \delta ;\delta $
. We have, by Lemma A.2, that
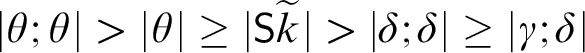 $|\theta ;\theta |> |\theta | \geq |{\sf S}\widetilde k| > |\delta ;\delta | \geq |\gamma ;\delta |$
.□
$|\theta ;\theta |> |\theta | \geq |{\sf S}\widetilde k| > |\delta ;\delta | \geq |\gamma ;\delta |$
.□
Consider any
![]() ${\mathcal A}$
-string
${\mathcal A}$
-string
![]() $\zeta $
. Let us say that
$\zeta $
. Let us say that
![]() $\zeta $
is essential if, for some n, we have
$\zeta $
is essential if, for some n, we have
![]() $\zeta =\beta _n$
and
$\zeta =\beta _n$
and
![]() $\alpha _n = \gamma ;\delta $
, where
$\alpha _n = \gamma ;\delta $
, where
![]() $\mathsf {c}$
occurs in
$\mathsf {c}$
occurs in
![]() $\gamma $
. Otherwise, we call
$\gamma $
. Otherwise, we call
![]() $\zeta $
inessential.
$\zeta $
inessential.
The combination of Lemmas A.3 and A.4 tells us that the enumeration of the
![]() $\beta _n$
looks as follows. Suppose
$\beta _n$
looks as follows. Suppose
![]() $\zeta $
is non-empty. If
$\zeta $
is non-empty. If
![]() $\zeta $
is inessential it will be enumerated first as
$\zeta $
is inessential it will be enumerated first as
![]() $\beta _{{\sf gn}_4(\zeta ;\zeta )}$
. All occurrences of
$\beta _{{\sf gn}_4(\zeta ;\zeta )}$
. All occurrences of
![]() $\zeta $
in the enumeration will have the form
$\zeta $
in the enumeration will have the form
![]() $\beta _{{\sf gn}_4(\zeta ;\eta )}$
, where
$\beta _{{\sf gn}_4(\zeta ;\eta )}$
, where
![]() $\zeta $
is a sub-string of
$\zeta $
is a sub-string of
![]() $\eta $
. If
$\eta $
. If
![]() $\zeta $
is essential, its first occurrence will be
$\zeta $
is essential, its first occurrence will be
![]() $\beta _{{\sf gn}_4(\gamma ,\delta )}$
, where
$\beta _{{\sf gn}_4(\gamma ,\delta )}$
, where
![]() $\gamma ,\delta $
is adequate and
$\gamma ,\delta $
is adequate and
![]() $\mathsf {c}$
occurs in
$\mathsf {c}$
occurs in
![]() $\gamma $
and
$\gamma $
and
 $\zeta = \gamma [\mathsf {c}:= {\sf S}(\widetilde {{\sf gn}_4(\delta ;\delta )})]$
. After that the enumeration mirrors the inessential case.
$\zeta = \gamma [\mathsf {c}:= {\sf S}(\widetilde {{\sf gn}_4(\delta ;\delta )})]$
. After that the enumeration mirrors the inessential case.
Remark A.5. We note that we could define a many-valued Gödel numbering
![]() ${\sf gn}^{\ast }(\zeta ) := \{ n\mid \zeta = \beta _n \}$
. There are no fundamental objections to many-valued Gödel numberings as long as they are total, in the sense that to each string a non-empty set of values is assigned, and injective, in the sense that the sets of values assigned to two different strings are disjoint. However, since in our framework, we opted for the more conventional choice of functional Gödel numberings, we will not consider a Gödel numbering like
${\sf gn}^{\ast }(\zeta ) := \{ n\mid \zeta = \beta _n \}$
. There are no fundamental objections to many-valued Gödel numberings as long as they are total, in the sense that to each string a non-empty set of values is assigned, and injective, in the sense that the sets of values assigned to two different strings are disjoint. However, since in our framework, we opted for the more conventional choice of functional Gödel numberings, we will not consider a Gödel numbering like
![]() ${\sf gn}^{\ast }$
.
${\sf gn}^{\ast }$
.
We define, for an
![]() ${\mathcal A}$
-string
${\mathcal A}$
-string
![]() $\theta $
:
$\theta $
:
![]() ${\sf gn}_5(\theta )$
is the smallest n such that
${\sf gn}_5(\theta )$
is the smallest n such that
![]() $\beta _n= \theta $
.
$\beta _n= \theta $
.
We could compute
![]() ${\sf gn}_5$
as follows. Let an
${\sf gn}_5$
as follows. Let an
![]() ${\mathcal A}$
-string
${\mathcal A}$
-string
![]() $\zeta $
be given.
$\zeta $
be given.
Is
![]() $\zeta $
the empty string? If yes,
$\zeta $
the empty string? If yes,
![]() ${\sf gn}_5(\zeta ) :=0$
. If no, does
${\sf gn}_5(\zeta ) :=0$
. If no, does
![]() $\zeta $
have a sub-string of the form
$\zeta $
have a sub-string of the form
![]() ${\sf S}\widetilde {k}$
? If no, set
${\sf S}\widetilde {k}$
? If no, set
![]() ${\sf gn}_5(\zeta ) := {\sf gn}_4(\zeta ;\zeta )$
. If yes, find the largest such k, say it is n. Let
${\sf gn}_5(\zeta ) := {\sf gn}_4(\zeta ;\zeta )$
. If yes, find the largest such k, say it is n. Let
![]() $\gamma $
be the result of replacing all occurrences of
$\gamma $
be the result of replacing all occurrences of
![]() ${\sf S}\widetilde {n}$
in
${\sf S}\widetilde {n}$
in
![]() $\zeta $
by
$\zeta $
by
![]() $\mathsf {c}$
. Is
$\mathsf {c}$
. Is
![]() $\alpha _n$
of the form
$\alpha _n$
of the form
![]() $\,\delta ;\delta $
, where
$\,\delta ;\delta $
, where
![]() $\gamma ;\delta $
is adequate? If no, set
$\gamma ;\delta $
is adequate? If no, set
![]() ${\sf gn}_5(\zeta ) := {\sf gn}_4(\zeta ;\zeta )$
. If yes, put
${\sf gn}_5(\zeta ) := {\sf gn}_4(\zeta ;\zeta )$
. If yes, put
![]() ${\sf gn}_5(\zeta ):= {\sf gn}_4(\gamma ;\delta )$
.
${\sf gn}_5(\zeta ):= {\sf gn}_4(\gamma ;\delta )$
.
The Gödel numbering
![]() ${\sf gn}_5$
is not monotonic with respect to the sub-string ordering and
${\sf gn}_5$
is not monotonic with respect to the sub-string ordering and
![]() $\leq $
. Suppose, e.g.,
$\leq $
. Suppose, e.g.,
![]() $n = {\sf gn}_4(\delta ;\delta )$
. Clearly,
$n = {\sf gn}_4(\delta ;\delta )$
. Clearly,
![]() $\widetilde {n}$
is inessential, since it does not contain any sub-string of the form
$\widetilde {n}$
is inessential, since it does not contain any sub-string of the form
![]() ${\sf S}\widetilde k$
. We remind the reader that
${\sf S}\widetilde k$
. We remind the reader that
![]() $|\widetilde {n}|= 7n+1$
. So, we have:
$|\widetilde {n}|= 7n+1$
. So, we have:
 $$ \begin{align*} {\sf gn}_5(\widetilde{n}) & = {\sf gn}_4(\widetilde{n};\widetilde{n}) \geq \frac{19^{14n+3}-1}{18}>n, \\ {\sf gn}_5({\sf S}\widetilde{n}) & = {\sf gn}_4(c;\delta)< {\sf gn}_4(\delta;\delta) = n. \end{align*} $$
$$ \begin{align*} {\sf gn}_5(\widetilde{n}) & = {\sf gn}_4(\widetilde{n};\widetilde{n}) \geq \frac{19^{14n+3}-1}{18}>n, \\ {\sf gn}_5({\sf S}\widetilde{n}) & = {\sf gn}_4(c;\delta)< {\sf gn}_4(\delta;\delta) = n. \end{align*} $$
So,
![]() ${\sf gn}_5({\sf S}\widetilde {n}) < {\sf gn}_5(\widetilde {n})$
.
${\sf gn}_5({\sf S}\widetilde {n}) < {\sf gn}_5(\widetilde {n})$
.
We will prove two lemmas about classes of cases where
![]() ${\sf gn}_5$
is monotonic.
${\sf gn}_5$
is monotonic.
Lemma A.6. Suppose
![]() $\zeta $
is inessential and
$\zeta $
is inessential and
![]() $\theta $
is a sub-string of
$\theta $
is a sub-string of
![]() $\zeta $
. Then,
$\zeta $
. Then,
![]() ${\sf gn}_5(\theta ) \leq {\sf gn}_5(\zeta )$
.
${\sf gn}_5(\theta ) \leq {\sf gn}_5(\zeta )$
.
Proof. Suppose
![]() $\zeta $
is inessential. Then,
$\zeta $
is inessential. Then,
![]() ${\sf gn}_5(\theta ) \leq {\sf gn}_4(\theta ;\theta ) \leq {\sf gn}_4(\zeta ;\zeta )= {\sf gn}_5(\zeta )$
.□
${\sf gn}_5(\theta ) \leq {\sf gn}_4(\theta ;\theta ) \leq {\sf gn}_4(\zeta ;\zeta )= {\sf gn}_5(\zeta )$
.□
Let
![]() ${\mathscr W\ }$
be the set of well-formed expressions of the arithmetical language. We partition
${\mathscr W\ }$
be the set of well-formed expressions of the arithmetical language. We partition
![]() ${\mathscr W\ }$
in two classes
${\mathscr W\ }$
in two classes
![]() ${\mathscr W}_0$
and
${\mathscr W}_0$
and
![]() ${\mathscr W}_1$
. Here:
${\mathscr W}_1$
. Here:
-
•
 ${\mathscr W}_0 := \{ {\sf SS}{\sf 0} \} \cup \{ \widetilde {n} \mid n \in \omega \} \cup \{ ({\sf SS}{\sf 0} \times \widetilde {n}) \mid n \in \omega \}$
${\mathscr W}_0 := \{ {\sf SS}{\sf 0} \} \cup \{ \widetilde {n} \mid n \in \omega \} \cup \{ ({\sf SS}{\sf 0} \times \widetilde {n}) \mid n \in \omega \}$
-
•
 ${\mathscr W}_1 := {\mathscr W}\ \setminus {\mathscr W}_0$
${\mathscr W}_1 := {\mathscr W}\ \setminus {\mathscr W}_0$
Lemma A.7. Suppose
![]() $\theta \in {\mathscr W}_1$
and
$\theta \in {\mathscr W}_1$
and
![]() $\zeta \in {\mathscr W}$
. Suppose further that
$\zeta \in {\mathscr W}$
. Suppose further that
![]() $\theta $
is a sub-expression of
$\theta $
is a sub-expression of
![]() $\zeta $
. Then,
$\zeta $
. Then,
![]() ${\sf gn}_5(\theta ) \leq {\sf gn}_5(\zeta )$
.
${\sf gn}_5(\theta ) \leq {\sf gn}_5(\zeta )$
.
Proof. Suppose
![]() ${\sf gn}_5(\zeta )= {\sf gn}_4(\gamma ;\delta )$
. Let
${\sf gn}_5(\zeta )= {\sf gn}_4(\gamma ;\delta )$
. Let
![]() $n := {\sf gn}_4(\delta ;\delta )$
and let
$n := {\sf gn}_4(\delta ;\delta )$
and let
![]() $\theta _0$
be the result of replacing all occurrences of
$\theta _0$
be the result of replacing all occurrences of
![]() ${\sf S} \widetilde {n}$
in
${\sf S} \widetilde {n}$
in
![]() $\theta $
by
$\theta $
by
![]() $\mathsf {c}$
. (We include the case here where there are no such occurrences.)
$\mathsf {c}$
. (We include the case here where there are no such occurrences.)
We claim that
![]() $\theta _0$
is a sub-expression of
$\theta _0$
is a sub-expression of
![]() $\gamma $
. To see this consider the parse-tree of
$\gamma $
. To see this consider the parse-tree of
![]() $\zeta $
. Since
$\zeta $
. Since
![]() $\theta $
is in
$\theta $
is in
![]() ${\mathscr W}_1$
, it cannot occur strictly below a node labeled
${\mathscr W}_1$
, it cannot occur strictly below a node labeled
![]() ${\sf S} \widetilde {n}$
. So, relabeling the nodes labeled
${\sf S} \widetilde {n}$
. So, relabeling the nodes labeled
![]() ${\sf S} \widetilde {n}$
with
${\sf S} \widetilde {n}$
with
![]() $\mathsf {c}$
and removing all nodes below them in the parse-tree of
$\mathsf {c}$
and removing all nodes below them in the parse-tree of
![]() $\zeta $
will result in occurrences of
$\zeta $
will result in occurrences of
![]() $\theta _0$
at the places where we originally had occurrences of
$\theta _0$
at the places where we originally had occurrences of
![]() $\theta $
.
$\theta $
.
It follows that
![]() ${\sf gn}_5(\theta ) \leq {\sf gn}_4(\theta _0;\delta ) \leq {\sf gn}_4(\gamma ;\delta )= {\sf gn}_5(\zeta )$
.□
${\sf gn}_5(\theta ) \leq {\sf gn}_4(\theta _0;\delta ) \leq {\sf gn}_4(\gamma ;\delta )= {\sf gn}_5(\zeta )$
.□
A.3 On
 ${\sf gn}_6$
${\sf gn}_6$
Finally, we are ready and set to define the desired Gödel numbering
![]() ${\sf gn}_6$
.
${\sf gn}_6$
.
-
•
 ${\sf gn}_6({\sf SS}{\sf 0}) = 2$
${\sf gn}_6({\sf SS}{\sf 0}) = 2$
-
•
 ${\sf gn}_6(\widetilde {n}) := 4n+1$
${\sf gn}_6(\widetilde {n}) := 4n+1$
-
•
 ${\sf gn}_6(({\sf SS}{\sf 0} \times \widetilde {n})):= 4n+3$
${\sf gn}_6(({\sf SS}{\sf 0} \times \widetilde {n})):= 4n+3$
-
•
 ${\sf gn}_6(\alpha ) := 2^{\,{\sf gn}_5(\alpha )}$
, if
${\sf gn}_6(\alpha ) := 2^{\,{\sf gn}_5(\alpha )}$
, if
 $\alpha $
is in
$\alpha $
is in
 ${\mathscr W}_1$
.
${\mathscr W}_1$
.
We have:
Lemma A.8.
![]() ${\sf gn}_6$
is injective on
${\sf gn}_6$
is injective on
![]() ${\mathscr W}$
.
${\mathscr W}$
.
Proof. Suppose
![]() $\alpha $
is well-formed. The only case where we could go wrong is where
$\alpha $
is well-formed. The only case where we could go wrong is where
![]() ${\sf gn}_5(\alpha )$
is 0 or 1. Since
${\sf gn}_5(\alpha )$
is 0 or 1. Since
![]() $\alpha $
is well-formed, it is not the empty string. So, for some adequate
$\alpha $
is well-formed, it is not the empty string. So, for some adequate
![]() $\gamma ;\delta $
, where
$\gamma ;\delta $
, where
![]() $\gamma $
is well-formed, we have
$\gamma $
is well-formed, we have
![]() ${\sf gn}_5(\alpha ) ={\sf gn}_4(\gamma ;\delta )$
. We note that
${\sf gn}_5(\alpha ) ={\sf gn}_4(\gamma ;\delta )$
. We note that
![]() $|\gamma ;\delta |\geq 3$
, so
$|\gamma ;\delta |\geq 3$
, so
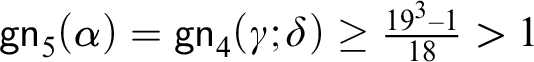 ${\sf gn}_5(\alpha ) ={\sf gn}_4(\gamma ;\delta ) \geq \frac {19^3-1}{18}> 1$
.□
${\sf gn}_5(\alpha ) ={\sf gn}_4(\gamma ;\delta ) \geq \frac {19^3-1}{18}> 1$
.□
So
![]() ${\sf gn}_6$
is indeed a Gödel numbering.
${\sf gn}_6$
is indeed a Gödel numbering.
Lemma A.9. Suppose
![]() $\alpha $
is in
$\alpha $
is in
![]() ${\mathscr W}_0$
. Then,
${\mathscr W}_0$
. Then,
![]() ${\sf gn}_6(\alpha ) \leq |\alpha | \leq {\sf gn}_4(\alpha ) \leq {\sf gn}_5(\alpha ) $
.
${\sf gn}_6(\alpha ) \leq |\alpha | \leq {\sf gn}_4(\alpha ) \leq {\sf gn}_5(\alpha ) $
.
Proof. Suppose
![]() $\alpha $
is in
$\alpha $
is in
![]() ${\mathscr W}_0$
. We note that, for no k, we have
${\mathscr W}_0$
. We note that, for no k, we have
![]() ${\sf S}\widetilde k$
is a sub-string of
${\sf S}\widetilde k$
is a sub-string of
![]() $\alpha $
. So,
$\alpha $
. So,
![]() ${\sf gn}_5(\alpha ) = {\sf gn}_4(\alpha ;\alpha )$
. It follows that
${\sf gn}_5(\alpha ) = {\sf gn}_4(\alpha ;\alpha )$
. It follows that
![]() $|\alpha | \leq {\sf gn}_4(\alpha ) \leq {\sf gn}_4(\alpha ;\alpha )= {\sf gn}_5(\alpha )$
. Moreover, we have:
$|\alpha | \leq {\sf gn}_4(\alpha ) \leq {\sf gn}_4(\alpha ;\alpha )= {\sf gn}_5(\alpha )$
. Moreover, we have:
 $$ \begin{align*} {\sf gn}_6({\sf SS}{\sf 0}) & = 2 < |{\sf SS}{\sf 0}| \\ {\sf gn}_6(\widetilde{n})& = 4n+1 \leq 7n+1 = |\widetilde{n}|\\ {\sf gn}_6(({\sf SS}{\sf 0} \times \widetilde{n})) & = 4n+3 < 7n+6 = |({\sf SS}{\sf 0} \times \widetilde{n})|. \\[-33pt]\end{align*} $$
$$ \begin{align*} {\sf gn}_6({\sf SS}{\sf 0}) & = 2 < |{\sf SS}{\sf 0}| \\ {\sf gn}_6(\widetilde{n})& = 4n+1 \leq 7n+1 = |\widetilde{n}|\\ {\sf gn}_6(({\sf SS}{\sf 0} \times \widetilde{n})) & = 4n+3 < 7n+6 = |({\sf SS}{\sf 0} \times \widetilde{n})|. \\[-33pt]\end{align*} $$
□
Lemma A.10. Suppose
![]() ${\sf S}\widetilde {n}$
is essential. Then,
${\sf S}\widetilde {n}$
is essential. Then,
![]() ${\sf gn}_6(\widetilde {n})<{\sf gn}_6({\sf S}\widetilde {n})$
${\sf gn}_6(\widetilde {n})<{\sf gn}_6({\sf S}\widetilde {n})$
Proof. Suppose
![]() ${\sf S}\widetilde {n}$
is essential. Since
${\sf S}\widetilde {n}$
is essential. Since
![]() ${\sf S}\widetilde {n}$
cannot have a proper subterm of the form
${\sf S}\widetilde {n}$
cannot have a proper subterm of the form
![]() ${\sf S}\widetilde m$
, we find that
${\sf S}\widetilde m$
, we find that
![]() ${\sf gn}_5({\sf S}\widetilde {n}) = {\sf gn}_4(c;\delta )$
for some
${\sf gn}_5({\sf S}\widetilde {n}) = {\sf gn}_4(c;\delta )$
for some
![]() $\delta $
that contains
$\delta $
that contains
![]() $\mathsf {c}$
. Moreover,
$\mathsf {c}$
. Moreover,
![]() $n = {\sf gn}_4(\delta ;\delta )$
. We have:
$n = {\sf gn}_4(\delta ;\delta )$
. We have:
 $$ \begin{align*} {\sf gn}_6(\widetilde{n}) & = 4n+1 \\ & < 4\frac{19^{2|\delta|+2}-1}{18} + 1 \\ & < 2^{\frac{19^{|\delta|+2}-1}{18}} \\ & \leq 2^n. \\[-33pt]\end{align*} $$
$$ \begin{align*} {\sf gn}_6(\widetilde{n}) & = 4n+1 \\ & < 4\frac{19^{2|\delta|+2}-1}{18} + 1 \\ & < 2^{\frac{19^{|\delta|+2}-1}{18}} \\ & \leq 2^n. \\[-33pt]\end{align*} $$
□
Lemma A.11.
![]() ${\sf gn}_6$
restricted to
${\sf gn}_6$
restricted to
![]() ${\mathscr W\ }$
is monotonic w.r.t. the sub-expression ordering and
${\mathscr W\ }$
is monotonic w.r.t. the sub-expression ordering and
![]() $<$
.
$<$
.
Proof. Suppose
![]() $\theta $
is a sub-expression of
$\theta $
is a sub-expression of
![]() $\zeta $
.
$\zeta $
.
Case 1: Suppose
![]() $\theta \in {\mathscr W}_1$
. Then, we are immediately done by Lemma A.7.
$\theta \in {\mathscr W}_1$
. Then, we are immediately done by Lemma A.7.
Case 2: Suppose
![]() $\theta \in {\mathscr W}_0$
.
$\theta \in {\mathscr W}_0$
.
Case 2.1: Suppose
![]() $\zeta \in {\mathscr W}_0$
. Then, we are done, by inspection of the definition of
$\zeta \in {\mathscr W}_0$
. Then, we are done, by inspection of the definition of
![]() ${\sf gn}_6$
on
${\sf gn}_6$
on
![]() ${\mathscr W}_0$
.
${\mathscr W}_0$
.
Case 2.2: Suppose
![]() $\zeta \in {\mathscr W}_1$
.
$\zeta \in {\mathscr W}_1$
.
Case 2.2.1: Suppose
![]() $\zeta $
is inessential. Then, by Lemma A.9,
$\zeta $
is inessential. Then, by Lemma A.9,
![]() ${\sf gn}_6(\theta ) \leq {\sf gn}_5(\theta )$
and, by Lemma A.6,
${\sf gn}_6(\theta ) \leq {\sf gn}_5(\theta )$
and, by Lemma A.6,
![]() ${\sf gn}_5(\theta ) \leq {\sf gn}_5(\zeta )$
. Hence,
${\sf gn}_5(\theta ) \leq {\sf gn}_5(\zeta )$
. Hence,
 $$ \begin{align*} {\sf gn}_6(\theta) \leq {\sf gn}_5(\theta) \leq {\sf gn}_5(\zeta) < 2^{{\sf gn}_5(\zeta)}= {\sf gn}_6(\zeta).\\[-15pt]\end{align*} $$
$$ \begin{align*} {\sf gn}_6(\theta) \leq {\sf gn}_5(\theta) \leq {\sf gn}_5(\zeta) < 2^{{\sf gn}_5(\zeta)}= {\sf gn}_6(\zeta).\\[-15pt]\end{align*} $$
Case 2.2.2: Suppose
![]() $\zeta $
is essential. It follows that
$\zeta $
is essential. It follows that
![]() ${\sf gn}_5(\zeta )= {\sf gn}_4(\gamma ;\delta )$
, where
${\sf gn}_5(\zeta )= {\sf gn}_4(\gamma ;\delta )$
, where
![]() $\mathsf {c}$
occurs in
$\mathsf {c}$
occurs in
![]() $\gamma $
. Let
$\gamma $
. Let
![]() $n := {\sf gn}_4(\delta ;\delta )$
. By Lemma A.2, we see that
$n := {\sf gn}_4(\delta ;\delta )$
. By Lemma A.2, we see that
![]() $|\widetilde {n}|> |\gamma |$
. It follows that any subterm of
$|\widetilde {n}|> |\gamma |$
. It follows that any subterm of
![]() $\gamma $
that is in
$\gamma $
that is in
![]() ${\mathscr W}_0$
must be a subterm of
${\mathscr W}_0$
must be a subterm of
![]() $\widetilde {n}$
. Hence, any subterm of
$\widetilde {n}$
. Hence, any subterm of
![]() $\zeta $
that is in
$\zeta $
that is in
![]() ${\mathscr W}_0$
must be in
${\mathscr W}_0$
must be in
![]() $\widetilde {n}$
. So, by Case 2.1,
$\widetilde {n}$
. So, by Case 2.1,
![]() ${\sf gn}_6(\theta ) \leq {\sf gn}_6(\widetilde {n})$
. Also, clearly,
${\sf gn}_6(\theta ) \leq {\sf gn}_6(\widetilde {n})$
. Also, clearly,
![]() ${\sf S} \widetilde {n}$
is essential, so, by Lemma A.10,
${\sf S} \widetilde {n}$
is essential, so, by Lemma A.10,
![]() ${\sf gn}_6(\widetilde {n}) < {\sf gn}_6({\sf S}\widetilde {n})$
. Finally, by Case 1:
${\sf gn}_6(\widetilde {n}) < {\sf gn}_6({\sf S}\widetilde {n})$
. Finally, by Case 1:
![]() ${\sf gn}_6({\sf S}\widetilde {n})\leq {\sf gn}_6(\zeta )$
. So,
${\sf gn}_6({\sf S}\widetilde {n})\leq {\sf gn}_6(\zeta )$
. So,
![]() ${\sf gn}_6(\theta ) \leq {\sf gn}_6(\zeta )$
.□
${\sf gn}_6(\theta ) \leq {\sf gn}_6(\zeta )$
.□
We end with the obvious insight that
![]() ${\sf gn}_6$
is self-referential.
${\sf gn}_6$
is self-referential.
Lemma A.12. Consider any arithmetical formula
![]() $A(x)$
in which there is a free occurrence of x. Let
$A(x)$
in which there is a free occurrence of x. Let
![]() $n = {\sf gn}_4(A(\mathsf {c});A(\mathsf {c}))$
and let
$n = {\sf gn}_4(A(\mathsf {c});A(\mathsf {c}))$
and let
![]() $k = 2^n$
. Then,
$k = 2^n$
. Then,
![]() $k = {\sf gn}_6(A(\overline k))$
.
$k = {\sf gn}_6(A(\overline k))$
.
Proof. We have
![]() ${\sf gn}_5(A(\overline k)) = {\sf gn}_4(A(\mathsf {c});A(\mathsf {c}))$
by the definition of
${\sf gn}_5(A(\overline k)) = {\sf gn}_4(A(\mathsf {c});A(\mathsf {c}))$
by the definition of
![]() ${\sf gn}_5$
. By the definition of
${\sf gn}_5$
. By the definition of
![]() ${\sf gn}_6$
, we get
${\sf gn}_6$
, we get
 ${\sf gn}_6(A(\overline k)) = 2^{\,{\sf gn}_5(A(\overline k))} = 2^n = k$
.□
${\sf gn}_6(A(\overline k)) = 2^{\,{\sf gn}_5(A(\overline k))} = 2^n = k$
.□
We may conclude:
Theorem A.13. The function
![]() ${\sf gn}_6$
is a monotonic Gödel numbering that is self-referential for dyadic numerals.
${\sf gn}_6$
is a monotonic Gödel numbering that is self-referential for dyadic numerals.
We note that our Gödel numbering is elementary and the tracking functions for the connectives also will be elementary.