Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T22:01:00.513Z Has data issue: false hasContentIssue false
  • English
  • Français

REPRESENTING CONJUNCTIVE DEDUCTIONS BY DISJUNCTIVE DEDUCTIONS

Published online by Cambridge University Press:  25 October 2016

KOSTA DOŠEN  and
ZORAN PETRIĆ
KOSTA DOŠEN*
Affiliation:
Mathematical Institute SANU
ZORAN PETRIĆ*
Affiliation:
Mathematical Institute SANU
*
*MATHEMATICAL INSTITUTE SANU KNEZ MIHAILOVA 36, P.F. 367 11001 BELGRADE, SERBIA E-mail: [email protected]
†MATHEMATICAL INSTITUTE SANU KNEZ MIHAILOVA 36, P.F. 367 11001 BELGRADE, SERBIA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A skeleton of the category with finite coproducts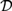${\cal D}$ freely generated by a single object has a subcategory isomorphic to a skeleton of the category with finite products 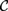${\cal C}$ freely generated by a countable set of objects. As a consequence, we obtain that 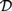${\cal D}$ has a subcategory equivalent with 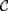${\cal C}$. From a proof-theoretical point of view, this means that up to some identifications of formulae the deductions of pure conjunctive logic with a countable set of propositional letters can be represented by deductions in pure disjunctive logic with just one propositional letter. By taking opposite categories, one can replace coproduct by product, i.e., disjunction by conjunction, and the other way round, to obtain the dual results.

Type
Research Article
Information
The Review of Symbolic Logic , Volume 10 , Issue 1 , March 2017 , pp. 145 - 157
Copyright
Copyright © Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Čubrić, Dj. (1998). Embedding of a free cartesian closed category into the category of sets. Journal of Pure and Applied Algebra, 126, 121–147.CrossRefGoogle Scholar
Došen, K. (1998). Functions redefined. The American Mathematical Monthly, 105, 631–635.CrossRefGoogle Scholar
Došen, K. (1999). Cut Elimination in Categories. Dordrecht: Kluwer.CrossRefGoogle Scholar
Došen, K. (2014). Algebras of deductions in category theory. In Jokanović, D., editor. Third Mathematical Conference of the Republic of Srpska, Proceedings, Trebinje 2013, Zbornik radova, Vol. I. Trebinje: Univerzitet u Istočnom Sarajevu, Fakultet za proizvodnju i menadžment, pp. 11–18 (available at: http://www.mi.sanu.ac.rs/∼kosta/publications.htm).Google Scholar
Došen, K. (2015). General proof theory. In Schroeder-Heister, P., Heinzmann, G., Hodges, W., and Bour, P. E., editors. Logic, Methodology and Philosophy of Science - Proceedings of the 14th International Congress (Nancy): Logic and Science Facing the New Technologies. Introduction to the Symposium on General Proof Theory. London: College Publications, pp. 149–151 (preprint available at: http://www.mi.sanu.ac.rs/∼kosta/publications.htm).Google Scholar
Došen, K. (2016). On the paths of categories: An introduction to deduction. In Piecha, T. and Schroeder-Heister, P., editors. Advances in Proof-Theoretic Semantics. Cham: Springer, pp. 65–77 (available at: http://www.mi.sanu.ac.rs/∼kosta/publications.htm).CrossRefGoogle Scholar
Došen, K. & Petrić, Z. (2001). The maximality of cartesian categories. Mathematical Logic Quarterly, 47, 137–144.Google Scholar
Došen, K. & Petrić, Z. (2003a). A Brauerian representation of split preorders. Mathematical Logic Quarterly, 49, 579–586 (version with misprints corrected available at arXiv).Google Scholar
Došen, K. & Petrić, Z. (2003b). Generality of proofs and its Brauerian representation. The Journal of Symbolic Logic, 68, 740–750.Google Scholar
Došen, K. & Petrić, Z. (2004). Proof-Theoretical Coherence. London: KCL Publications (College Publications) (revised version of 2007 available at: http://www.mi.sanu.ac.rs/∼kosta/coh.pdf).Google Scholar
Došen, K. & Petrić, Z. (2007). Proof-Net Categories. Monza: Polimetrica (preprint of 2005 available at: http://www.mi.sanu.ac.rs/kosta/pn.pdf).Google Scholar
Došen, K. & Petrić, Z. (2013). Syntax for split preorders. Annals of Pure and Applied Logic, 164, 443–481.Google Scholar
Kelly, G. M. (1972). An abstract approach to coherence. In Mac Lane, S., editor. Coherence in Categories. Lecture Notes in Mathematics, Vol. 281. Berlin: Springer, pp. 106–147.Google Scholar
Lambek, J. (1972). Deductive systems and categories III: Cartesian closed categories, intuitionist propositional calculus, and combinatory logic. In Lawvere, F. W., editor. Toposes, Algebraic Geometry and Logic. Lecture Notes in Mathematics, Vol. 274. Berlin: Springer, pp. 57–82.CrossRefGoogle Scholar
Lambek, J. & Scott, P. J. (1986). Introduction to Higher-Order Categorical Logic. Cambridge: Cambridge University Press.Google Scholar
Lawvere, F. W. (1969). Adjointness in foundations. Dialectica, 23, 281–296.CrossRefGoogle Scholar
Mac Lane, S. (1965). Categorical algebra. Bulletin of the American Mathematical Society, 71, 40–106.Google Scholar
Mac Lane, S. (1971). Categories for the Working Mathematician. Berlin: Springer (expanded second edition, 1998).Google Scholar
Mints, G. E. (1980). Category theory and proof theory. Aktual’nye voprosy logiki i metodologii nauki. Kiev: Naukova Dumka, pp. 252–278 (in Russian) (English translation, with permuted title, in: G. E. Mints, Selected Papers in Proof Theory, Bibliopolis, Naples, 1992).Google Scholar
Petrić, Z. (2002). Coherence in substructural categories. Studia Logica, 70, 271–296.Google Scholar
Prawitz, D. (1971). Ideas and results in proof theory. In Fenstad, J. E., editor. Proceedings of the Second Scandinavian Logic Symposium. Amsterdam: North-Holland, pp. 235–307.Google Scholar
Troelstra, A. S. & Schwichtenberg, H. (1996). Basic Proof Theory. Cambridge: Cambridge University Press (second edition, 2000).Google Scholar