No CrossRef data available.
Article contents
A NOTE ON THE REVERSE MATHEMATICS OF THE SORITES
Published online by Cambridge University Press: 07 December 2018
Abstract
Sorites is an ancient piece of paradoxical reasoning pertaining to sets with the following properties: (Supervenience) elements of the set are mapped into some set of “attributes”; (Tolerance) if an element has a given attribute then so are the elements in some vicinity of this element; and (Connectedness) such vicinities can be arranged into pairwise overlapping finite chains connecting two elements with different attributes. Obviously, if Superveneince is assumed, then (1) Tolerance implies lack of Connectedness, and (2) Connectedness implies lack of Tolerance. Using a very general but precise definition of “vicinity”, Dzhafarov & Dzhafarov (2010) offered two formalizations of these mutual contrapositions. Mathematically, the formalizations are equally valid, but in this paper, we offer a different basis by which to compare them. Namely, we show that the formalizations have different proof-theoretic strengths when measured in the framework of reverse mathematics: the formalization of (1) is provable in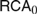 
$RC{A_0}$, while the formalization of (2) is equivalent to 
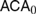$AC{A_0}$ over 
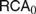$RC{A_0}$. Thus, in a certain precise sense, the approach of (1) is more constructive than that of (2).
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2018
References
BIBLIOGRAPHY
Devlin, K. (2009). Modeling real reasoning. In Sommaruga, G., editor. Formal Theories of Information: From Shannon to Semantic Information Theory and General Concepts of Information . Berlin: Springer, pp. 234–252.CrossRefGoogle Scholar
Dzhafarov, D. D. & Dzhafarov, E. N. Classificatory sorites, probabilistic supervenience, and rule-making. In Abasnezhad, A. and Bueno, O., editors. On the Sorites Paradox. Springer, to appear.Google Scholar
Dzhafarov, E. N. & Dzhafarov, D. D. (2010). Sorites without vagueness I: Classificatory sorites. Theoria, 76, 4–24.CrossRefGoogle Scholar
Hirschfeldt, D. R. (2015). Slicing the Truth: On the Computable and Reverse Mathematics of Combinatorial Principles, edited by Chon, C., Fen, Q., Slaman, T. A., Woodin, W. H., and Yang, Y.. Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore. Hackensack, NJ: World Scientific Publishing.Google Scholar
Marcone, A. (2007). Interval orders and reverse mathematics. Notre Dame Journal of Formal Logic, 48, 425–448. (electronic).CrossRefGoogle Scholar
Shore, R. A. (2010). Reverse mathematics: The playground of logic. Bulletin of Symbolic Logic, 16, 378–402.CrossRefGoogle Scholar
Sierpinski, W. (1952). General Topology. Mathematical Expositions, No. 7. Toronto: University of Toronto Press, translated by Krieger, C. Cecilia.Google Scholar
Simpson, S. G. (2009). Subsystems of Second Order Arithmetic (second edition). Perspectives in Logic. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Soare, R. I. (2016). Turing Computability: Theory and Applications. Theory and Applications of Computability. Berlin: Springer-Verlag.CrossRefGoogle Scholar
Stenning, K. & van Lambalgen, M. (2008). Human Reasoning and Cognitive Science. Boston: MIT Press.CrossRefGoogle Scholar
Weber, Z. & Colyvan, M. (2010). A topological sorites. Journal of Philosophy, 107, 311–325.CrossRefGoogle Scholar