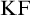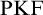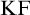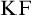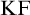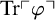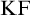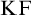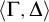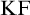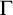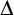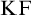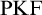1 Introduction
Kripke’s theory of truth [Reference Kripke12] is a cornerstone of contemporary research on truth and the semantic paradoxes. The theory provides us with a strategy for constructing, that is defining, desirable interpretations of a self-applicable truth predicate as the fixed points of a certain monotone operator (so-called Kripke Jump). These fixed points can serve as interpretations of the truth predicate within non-classical models of the language, as in Kripke’s original article, but can also be used in combination with classical models, so-called closed-off models.Footnote
1
Feferman [Reference Feferman6] devised an elegant axiomatic theory of the Kripkean truth predicate of these closed-off fixed-point models. The theory is known as Kripke–Feferman (
![]() $\mathrm {KF}$
) and is still one of the most popular axiomatic truth theories in the literature formulated in classical logic.Footnote
2
Nonetheless,
$\mathrm {KF}$
) and is still one of the most popular axiomatic truth theories in the literature formulated in classical logic.Footnote
2
Nonetheless,
![]() $\mathrm {KF}$
displays a number of unintended and slightly bizarre features, which it inherits from the behavior of the truth predicate in the closed-off fixed-point models. While in the non-classical fixed-point models the truth predicate is transparent, i.e.,
$\mathrm {KF}$
displays a number of unintended and slightly bizarre features, which it inherits from the behavior of the truth predicate in the closed-off fixed-point models. While in the non-classical fixed-point models the truth predicate is transparent, i.e.,
![]() $\varphi $
and
$\varphi $
and
![]() $\mathrm{Tr}\ulcorner {\varphi }\urcorner $
will always receive the same semantic value (if they receive any), this no longer holds in the closed-off models. Rather, for each closed-off model there will be sentences
$\mathrm{Tr}\ulcorner {\varphi }\urcorner $
will always receive the same semantic value (if they receive any), this no longer holds in the closed-off models. Rather, for each closed-off model there will be sentences
![]() $\varphi $
, e.g., the Liar sentence, such that either
$\varphi $
, e.g., the Liar sentence, such that either
![]() $\varphi $
and
$\varphi $
and
![]() $\neg \mathrm{Tr}\ulcorner {\varphi }\urcorner $
will be true in the model, or
$\neg \mathrm{Tr}\ulcorner {\varphi }\urcorner $
will be true in the model, or
![]() $\neg \varphi $
and
$\neg \varphi $
and
![]() $\mathrm{Tr}\ulcorner {\varphi }\urcorner $
will be true in the model. As a consequence one can prove this counterintuitive disjunction in
$\mathrm{Tr}\ulcorner {\varphi }\urcorner $
will be true in the model. As a consequence one can prove this counterintuitive disjunction in
![]() $\mathrm {KF}$
for the Liar sentence
$\mathrm {KF}$
for the Liar sentence
![]() $\lambda $
, i.e.,
$\lambda $
, i.e.,
Since the transparency of truth seems to be one of the basic characteristics of the truth predicate, the aforementioned asymmetry puts the idea of understanding the closed-off models as suitable models of an intuitively acceptable truth predicate under some stress and alongside casts doubt on
![]() $\mathrm {KF}$
as an acceptable theory of truth. However, reasoning within the non-classical logic of the Kripkean fixed-points seems a non-trivial affair or, as Feferman [Reference Feferman5, p. 95] would have it, “nothing like sustained ordinary reasoning can be carried on” in these non-classical logics. Giving up on
$\mathrm {KF}$
as an acceptable theory of truth. However, reasoning within the non-classical logic of the Kripkean fixed-points seems a non-trivial affair or, as Feferman [Reference Feferman5, p. 95] would have it, “nothing like sustained ordinary reasoning can be carried on” in these non-classical logics. Giving up on
![]() $\mathrm {KF}$
thus hardly seems a desirable conclusion.
$\mathrm {KF}$
thus hardly seems a desirable conclusion.
In reaction to the counterintuitive consequences of
![]() $\mathrm {KF}$
, Reinhardt [Reference Reinhardt20, Reference Reinhardt21] proposed an instrumentalist interpretation of the theory in analogy to Hilbert’s program. Famously, Hilbert proposed to justify number theory, analysis and even richer mathematical theories by finitary means. Without entering into Hilbert-exegesis, the main idea was of course to provide consistency proofs for these mathematical theories in a finitistically acceptable metatheory. From a finitist perspective this would turn the mathematical theories into useful tools for producing mathematical truths. But the fate of Hilbert’s program, at least on its standard interpretation, is well known: Gödel’s incompleteness theorems are commonly thought to be the program’s coffin nail. Nonetheless Reinhardt [Reference Reinhardt20, Reference Reinhardt21] was optimistic that his own program had greater chances of success.Footnote
3
Reinhardt proposed to view
$\mathrm {KF}$
, Reinhardt [Reference Reinhardt20, Reference Reinhardt21] proposed an instrumentalist interpretation of the theory in analogy to Hilbert’s program. Famously, Hilbert proposed to justify number theory, analysis and even richer mathematical theories by finitary means. Without entering into Hilbert-exegesis, the main idea was of course to provide consistency proofs for these mathematical theories in a finitistically acceptable metatheory. From a finitist perspective this would turn the mathematical theories into useful tools for producing mathematical truths. But the fate of Hilbert’s program, at least on its standard interpretation, is well known: Gödel’s incompleteness theorems are commonly thought to be the program’s coffin nail. Nonetheless Reinhardt [Reference Reinhardt20, Reference Reinhardt21] was optimistic that his own program had greater chances of success.Footnote
3
Reinhardt proposed to view
![]() $\mathrm {KF}$
as a tool for deriving Kripkean truths in the same way Hilbert viewed, say, number theory as a tool for deriving mathematical truths. A Kripkean truth is a sentence that is true from the perspective of the Kripkean fixed points: if
$\mathrm {KF}$
as a tool for deriving Kripkean truths in the same way Hilbert viewed, say, number theory as a tool for deriving mathematical truths. A Kripkean truth is a sentence that is true from the perspective of the Kripkean fixed points: if
![]() $\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
(
$\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
(
![]() $\mathrm{Tr}\ulcorner {\neg \varphi }\urcorner $
), then
$\mathrm{Tr}\ulcorner {\neg \varphi }\urcorner $
), then
![]() $\varphi $
is true (false) in all non-classical fixed-point models, that is, we are guaranteed that
$\varphi $
is true (false) in all non-classical fixed-point models, that is, we are guaranteed that
![]() $\varphi $
receives a semantic value from the perspective of Kripke’s theory of truth. This is not a general feature of the theorems of
$\varphi $
receives a semantic value from the perspective of Kripke’s theory of truth. This is not a general feature of the theorems of
![]() $\mathrm {KF}$
but peculiar to those sentences that
$\mathrm {KF}$
but peculiar to those sentences that
![]() $\mathrm {KF}$
proves true (false). The latter sentences Reinhardt called “the significant part of
$\mathrm {KF}$
proves true (false). The latter sentences Reinhardt called “the significant part of
![]() $\mathrm {KF}$
” [Reference Reinhardt21, p. 242] and labelled the set of
$\mathrm {KF}$
” [Reference Reinhardt21, p. 242] and labelled the set of
![]() $\mathrm {KF}$
-significant sentences
$\mathrm {KF}$
-significant sentences
![]() $\mathrm {KFS}:=\{\varphi \mid \mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner \}$
.Footnote
4
In light of this terminology the constitutive question of Reinhardt’s program is whether it is possible “to justify the use of nonsignificant sentences entirely within the framework of significant sentences” [Reference Reinhardt21, p. 225].
$\mathrm {KFS}:=\{\varphi \mid \mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner \}$
.Footnote
4
In light of this terminology the constitutive question of Reinhardt’s program is whether it is possible “to justify the use of nonsignificant sentences entirely within the framework of significant sentences” [Reference Reinhardt21, p. 225].
But what would such a successful instrumentalist interpretation of
![]() $\mathrm {KF}$
and the use of non-significant sentences amount to? Reinhardt himself is scarce on the exact details and does not commit to a particular answer to this question. However, at the end of [Reference Reinhardt20], without explicitly addressing the question of an instrumentalist interpretation of
$\mathrm {KF}$
and the use of non-significant sentences amount to? Reinhardt himself is scarce on the exact details and does not commit to a particular answer to this question. However, at the end of [Reference Reinhardt20], without explicitly addressing the question of an instrumentalist interpretation of
![]() $\mathrm {KF}$
, Reinhardt asks the following question:
$\mathrm {KF}$
, Reinhardt asks the following question:
If
![]() $\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
is there a
$\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
is there a
![]() $\mathrm {KF}$
-proof
$\mathrm {KF}$
-proof
such that for each
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi _i}\urcorner $
? (cf. [Reference Reinhardt20, p. 239])Footnote
5
$\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi _i}\urcorner $
? (cf. [Reference Reinhardt20, p. 239])Footnote
5
If we were to answer this question positively, we could justify each Kripkean truth provable in
![]() $\mathrm {KF}$
by appealing solely to the significant fragment of
$\mathrm {KF}$
by appealing solely to the significant fragment of
![]() $\mathrm {KF}$
: even though we have reasoned in
$\mathrm {KF}$
: even though we have reasoned in
![]() $\mathrm {KF}$
, each step of our reasoning is part of KFS and hence remains “within the framework of significant sentences.” It is then suggestive to take the above question to be constitutive of Reinhardt’s program. Indeed, this interpretation of Reinhardt’s program is adopted by Halbach & Horsten [Reference Halbach and Horsten10], who called the question Reinhardt’s Problem. Unfortunately, as Halbach and Horsten convincingly argue, if understood in this way the instrumentalist interpretation of
$\mathrm {KF}$
, each step of our reasoning is part of KFS and hence remains “within the framework of significant sentences.” It is then suggestive to take the above question to be constitutive of Reinhardt’s program. Indeed, this interpretation of Reinhardt’s program is adopted by Halbach & Horsten [Reference Halbach and Horsten10], who called the question Reinhardt’s Problem. Unfortunately, as Halbach and Horsten convincingly argue, if understood in this way the instrumentalist interpretation of
![]() $\mathrm {KF}$
will fail. We refer to [Reference Halbach and Horsten10] for details but, in a nutshell, the reason for this failure is that the truth-theoretic axioms of
$\mathrm {KF}$
will fail. We refer to [Reference Halbach and Horsten10] for details but, in a nutshell, the reason for this failure is that the truth-theoretic axioms of
![]() $\mathrm {KF}$
will not be true in the non-classical fixed-point models and hence not be part of KFS, e.g., if
$\mathrm {KF}$
will not be true in the non-classical fixed-point models and hence not be part of KFS, e.g., if
![]() ,Footnote
6
then
,Footnote
6
then
![]() $\varphi _i\not \in \mathrm {KFS}$
. Indeed, Halbach & Horsten [Reference Halbach and Horsten10, p. 684] take this to show “that Reinhardt’s analogue of Hilbert’s program suffers the same fate as that of Hilbert’s program”.
$\varphi _i\not \in \mathrm {KFS}$
. Indeed, Halbach & Horsten [Reference Halbach and Horsten10, p. 684] take this to show “that Reinhardt’s analogue of Hilbert’s program suffers the same fate as that of Hilbert’s program”.
However, we think that this conclusion is premature and argue that, to the contrary, if suitably understood Reinhardt’s program has good chances of succeeding. Our key point of contention is that Halbach & Horsten [Reference Halbach and Horsten10], arguably following Reinhardt, employ the perspective of classical logic when theorizing about the significant part of
![]() $\mathrm {KF}$
. But the logic of the significant part of
$\mathrm {KF}$
. But the logic of the significant part of
![]() $\mathrm {KF}$
is not classical logic but the logic of the non-classical fixed-point models, that is, a non-classical logic. This observation has two interrelated consequences for Reinhardt’s program. First, contra Reinhardt, and contra Halbach and Horsten, we should not identify the significant part of
$\mathrm {KF}$
is not classical logic but the logic of the non-classical fixed-point models, that is, a non-classical logic. This observation has two interrelated consequences for Reinhardt’s program. First, contra Reinhardt, and contra Halbach and Horsten, we should not identify the significant part of
![]() $\mathrm {KF}$
exclusively with the set of significant sentences. Rather it also seems crucial to ask which inferences are admissible within the significant part of
$\mathrm {KF}$
exclusively with the set of significant sentences. Rather it also seems crucial to ask which inferences are admissible within the significant part of
![]() $\mathrm {KF}$
.Footnote
7
Of course, in classical logic this difference collapses due to the deduction theorem but not necessarily so in non-classical logics. For example, the three-valued logic Strong Kleene,
$\mathrm {KF}$
.Footnote
7
Of course, in classical logic this difference collapses due to the deduction theorem but not necessarily so in non-classical logics. For example, the three-valued logic Strong Kleene,
![]() ${\textsf {K}}\mathsf {3}$
, has no logical truth, but many valid inferences—if, in this case, we were to focus only on the theorems of the logic, there would be no logic to discuss. Moreover, since the significant sentences can be retrieved from the significant inferences, that is the provably true inferences, we should focus on the latter rather than the former in addressing Reinhardt’s Problem.Footnote
8
To this end, it is helpful to conceive of
${\textsf {K}}\mathsf {3}$
, has no logical truth, but many valid inferences—if, in this case, we were to focus only on the theorems of the logic, there would be no logic to discuss. Moreover, since the significant sentences can be retrieved from the significant inferences, that is the provably true inferences, we should focus on the latter rather than the former in addressing Reinhardt’s Problem.Footnote
8
To this end, it is helpful to conceive of
![]() $\mathrm {KF}$
as formulated in a two-sided sequent calculus. Let
$\mathrm {KF}$
as formulated in a two-sided sequent calculus. Let
![]() $\Gamma ,\Delta $
be finite sets of sentences and let
$\Gamma ,\Delta $
be finite sets of sentences and let
![]() $\mathrm{Tr}\ulcorner {\Gamma }\urcorner $
be short for
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner $
be short for
![]() $\{\mathrm{Tr}\ulcorner {\gamma }\urcorner \mid \gamma \in \Gamma \}$
. The admissible inferences of the significant part of
$\{\mathrm{Tr}\ulcorner {\gamma }\urcorner \mid \gamma \in \Gamma \}$
. The admissible inferences of the significant part of
![]() $\mathrm {KF}$
, which we label KFSI, can then be defined as follows:Footnote
9
$\mathrm {KF}$
, which we label KFSI, can then be defined as follows:Footnote
9
Second, Reinhardt’s Problem, according to the formulation of Halbach & Horsten [Reference Halbach and Horsten10], which admittedly was inspired by Reinhardt’s [Reference Reinhardt20] original question, conceives of
![]() $\mathrm {KF}$
-proofs as sequences of theorems of
$\mathrm {KF}$
-proofs as sequences of theorems of
![]() $\mathrm {KF}$
. But by focusing on sequences of theorems, we cannot fully exploit the significant part of
$\mathrm {KF}$
. But by focusing on sequences of theorems, we cannot fully exploit the significant part of
![]() $\mathrm {KF}$
, that is, KFSI for precisely the reasons Halbach & Horsten [Reference Halbach and Horsten10] used to rebut Reinhardt’s program: while double negation introduction is clearly a member of KFSI, proving this fact by a sequence of theorems would take us outside of KFS since it would use the truth-theoretic axiom
$\mathrm {KF}$
, that is, KFSI for precisely the reasons Halbach & Horsten [Reference Halbach and Horsten10] used to rebut Reinhardt’s program: while double negation introduction is clearly a member of KFSI, proving this fact by a sequence of theorems would take us outside of KFS since it would use the truth-theoretic axiom
![]() , which is not a member of the significant part of
, which is not a member of the significant part of
![]() $\mathrm {KF}$
. This suggests a reformulation of Reinhardt’s Problem in terms of a notion of proof that focuses on inferences rather than theorems. To this end, it proves useful again to formulate
$\mathrm {KF}$
. This suggests a reformulation of Reinhardt’s Problem in terms of a notion of proof that focuses on inferences rather than theorems. To this end, it proves useful again to formulate
![]() $\mathrm {KF}$
in a two-sided sequent calculus and to conceive of proofs as derivation trees, where each node of the tree is labeled by a sequent. As a matter of fact, in this case we can distinguish between two versions of Reinhardt’s Problem:
$\mathrm {KF}$
in a two-sided sequent calculus and to conceive of proofs as derivation trees, where each node of the tree is labeled by a sequent. As a matter of fact, in this case we can distinguish between two versions of Reinhardt’s Problem:
-
(1) For every
 $\mathrm {KF}$
-theorem of the form
$\mathrm {KF}$
-theorem of the form
 $\mathrm{Tr}\ulcorner {\varphi }\urcorner $
, is there a
$\mathrm{Tr}\ulcorner {\varphi }\urcorner $
, is there a
 $\mathrm {KF}$
-derivation
$\mathrm {KF}$
-derivation
 $\mathcal {D}$
of
$\mathcal {D}$
of
 $\varnothing \Rightarrow \mathrm{Tr}\ulcorner {\varphi }\urcorner $
such that every node d of
$\varnothing \Rightarrow \mathrm{Tr}\ulcorner {\varphi }\urcorner $
such that every node d of
 $\mathcal {D}$
is a significant inference?
$\mathcal {D}$
is a significant inference? -
(2) For every
 $\mathrm {KF}$
-derivable sequent of the form
$\mathrm {KF}$
-derivable sequent of the form
 $\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
, is there a
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
, is there a
 $\mathrm {KF}$
-derivation
$\mathrm {KF}$
-derivation
 $\mathcal {D}$
of
$\mathcal {D}$
of
 $\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
such that every node d of
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
such that every node d of
 $\mathcal {D}$
is a significant inference?
$\mathcal {D}$
is a significant inference?
The first question is a reformulation of Halbach & Horsten’s [Reference Halbach and Horsten10] Reinhardt’s Problem.Footnote
10
The second question, which we label Generalized Reinhardt Problem, asks whether all provably true inferences can be justified by appealing to the significant inferences only. Arguably, to deem Reinhardt’s program successful one needs to give an affirmative answer to the Generalized Reinhardt Problem.Footnote
11
Otherwise, a proof of
![]() $\mathrm{Tr}\ulcorner {\varphi }\urcorner $
could still rely on inferences that, whilst part of KFSI, cannot themselves be justified by appealing only to the significant inferences of
$\mathrm{Tr}\ulcorner {\varphi }\urcorner $
could still rely on inferences that, whilst part of KFSI, cannot themselves be justified by appealing only to the significant inferences of
![]() $\mathrm {KF}$
. In this paper, we shall argue that on this more careful formulation, Reinhardt’s program has good prospects of succeeding. We corroborate our assessment by giving an affirmative answer to the Generalized Reinhardt Problem for versions of
$\mathrm {KF}$
. In this paper, we shall argue that on this more careful formulation, Reinhardt’s program has good prospects of succeeding. We corroborate our assessment by giving an affirmative answer to the Generalized Reinhardt Problem for versions of
![]() $\mathrm {KF}$
with internal and restricted induction.
$\mathrm {KF}$
with internal and restricted induction.
Arguably, giving an affirmative answer to the Generalized Reinhardt Problem is at best a partial completion of Reinhardt’s program: what is still required is an independent axiomatization of the significant part of
![]() $\mathrm {KF}$
, for only this would prove
$\mathrm {KF}$
, for only this would prove
![]() $\mathrm {KF}$
dispensable. We will now take a fresh look at the question of an independent axiomatization, which Halbach and Horsten called Reinhardt’s Challenge [Reference Halbach and Horsten10, p. 689]. This will prove instrumental in answering Generalized Reinhardt Problem for the aforementioned versions of
$\mathrm {KF}$
dispensable. We will now take a fresh look at the question of an independent axiomatization, which Halbach and Horsten called Reinhardt’s Challenge [Reference Halbach and Horsten10, p. 689]. This will prove instrumental in answering Generalized Reinhardt Problem for the aforementioned versions of
![]() $\mathrm {KF}$
. Reinhardt [Reference Reinhardt20] asked for an independent axiomatization of the significant part of
$\mathrm {KF}$
. Reinhardt [Reference Reinhardt20] asked for an independent axiomatization of the significant part of
![]() $\mathrm {KF}$
. More precisely, Reinhardt [Reference Reinhardt20, p. 239] asked:
$\mathrm {KF}$
. More precisely, Reinhardt [Reference Reinhardt20, p. 239] asked:
-
(a) “Is there an axiomatization of
 $\{\sigma \mid \mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\sigma }\urcorner \}$
which is natural and formulated entirely within the domain of significant sentences,….”
$\{\sigma \mid \mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\sigma }\urcorner \}$
which is natural and formulated entirely within the domain of significant sentences,….” -
(b) “Similarly for the relation
 $\Gamma \vdash _{S}\sigma $
defined by
$\Gamma \vdash _{S}\sigma $
defined by
 $\mathrm {KF} + \{\mathrm{Tr}\ulcorner {\gamma } \urcorner \mid \gamma \in \Gamma \}\vdash\mathrm{Tr}\ulcorner {\sigma }\urcorner $
.”
$\mathrm {KF} + \{\mathrm{Tr}\ulcorner {\gamma } \urcorner \mid \gamma \in \Gamma \}\vdash\mathrm{Tr}\ulcorner {\sigma }\urcorner $
.”
Halbach & Horsten [Reference Halbach and Horsten10] proposed their theory Partial Kripke–Feferman (
![]() $\mathrm {PKF}$
) in way of answering Reinhardt’s Challenge.
$\mathrm {PKF}$
) in way of answering Reinhardt’s Challenge.
![]() $\mathrm {PKF}$
is formulated in a non-classical, two-sided sequent calculus and thus fits neatly with our observation that one should focus on the provably true inferences of
$\mathrm {PKF}$
is formulated in a non-classical, two-sided sequent calculus and thus fits neatly with our observation that one should focus on the provably true inferences of
![]() $\mathrm {KF}$
rather than the provably true sentences. Moreover,
$\mathrm {KF}$
rather than the provably true sentences. Moreover,
![]() $\mathrm {PKF}$
is arguably a natural axiomatization of Kripke’s theory of truth. However, Halbach & Horsten [Reference Halbach and Horsten10] observed that there are sentences
$\mathrm {PKF}$
is arguably a natural axiomatization of Kripke’s theory of truth. However, Halbach & Horsten [Reference Halbach and Horsten10] observed that there are sentences
![]() $\varphi $
such that
$\varphi $
such that
![]() $\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
but
$\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
but
![]() $\mathrm {PKF}\not \vdash \varphi $
, which led them to conclude that Reinhardt’s Challenge cannot be met. The reason for this asymmetry is due to the difference in proof-theoretic strength of
$\mathrm {PKF}\not \vdash \varphi $
, which led them to conclude that Reinhardt’s Challenge cannot be met. The reason for this asymmetry is due to the difference in proof-theoretic strength of
![]() $\mathrm {KF}$
and
$\mathrm {KF}$
and
![]() $\mathrm {PKF}$
: while
$\mathrm {PKF}$
: while
![]() $\mathrm {KF}$
proves transfinite induction for ordinals below
$\mathrm {KF}$
proves transfinite induction for ordinals below
![]() $\varepsilon _0$
,
$\varepsilon _0$
,
![]() $\mathrm {PKF}$
only proves transfinite induction for ordinals smaller than
$\mathrm {PKF}$
only proves transfinite induction for ordinals smaller than
![]() $\omega ^\omega $
. As a consequence, there will be arithmetical sentences that
$\omega ^\omega $
. As a consequence, there will be arithmetical sentences that
![]() $\mathrm {KF}$
proves true that
$\mathrm {KF}$
proves true that
![]() $\mathrm {PKF}$
cannot prove. The story does not end there however. First, as Halbach & Nicolai [Reference Halbach and Nicolai11] observe, the discrepancy between
$\mathrm {PKF}$
cannot prove. The story does not end there however. First, as Halbach & Nicolai [Reference Halbach and Nicolai11] observe, the discrepancy between
![]() $\mathrm {KF}$
and
$\mathrm {KF}$
and
![]() $\mathrm {PKF}$
arises only if the rule of induction is extended beyond the arithmetical language, that is, if we restrict induction to the language of arithmetic—call the resulting theories
$\mathrm {PKF}$
arises only if the rule of induction is extended beyond the arithmetical language, that is, if we restrict induction to the language of arithmetic—call the resulting theories
![]() $\mathrm {KF}^-$
and
$\mathrm {KF}^-$
and
![]() $\mathrm {PKF}^-$
—then
$\mathrm {PKF}^-$
—then
![]() $\mathrm {KF}^-\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
if, and only if,
$\mathrm {KF}^-\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
if, and only if,
![]() $\mathrm {PKF}^-\vdash \varphi $
. This highlights that the asymmetry between
$\mathrm {PKF}^-\vdash \varphi $
. This highlights that the asymmetry between
![]() $\mathrm {KF}$
and
$\mathrm {KF}$
and
![]() $\mathrm {PKF}$
is not due to the truth-specific principles but the amount of induction that is assumed in the respective theories. Second, corroborating the latter observation, Nicolai [Reference Nicolai14] showed that the asymmetry between
$\mathrm {PKF}$
is not due to the truth-specific principles but the amount of induction that is assumed in the respective theories. Second, corroborating the latter observation, Nicolai [Reference Nicolai14] showed that the asymmetry between
![]() $\mathrm {KF}$
and
$\mathrm {KF}$
and
![]() $\mathrm {PKF}$
is indeed solely due to the amount of induction available within the respective theories: Nicolai shows that if transfinite induction up to
$\mathrm {PKF}$
is indeed solely due to the amount of induction available within the respective theories: Nicolai shows that if transfinite induction up to
![]() $<\varepsilon _0$
is added axiomatically to
$<\varepsilon _0$
is added axiomatically to
![]() $\mathrm {PKF}$
—call this theory
$\mathrm {PKF}$
—call this theory
![]() $\mathrm {PKF}^+$
—then
$\mathrm {PKF}^+$
—then
![]() $\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
if, and only if,
$\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner $
if, and only if,
![]() $\mathrm {PKF}^+\vdash \varphi $
. Moreover, Nicolai [Reference Nicolai14] shows that independently of which version of induction is assumed in
$\mathrm {PKF}^+\vdash \varphi $
. Moreover, Nicolai [Reference Nicolai14] shows that independently of which version of induction is assumed in
![]() $\mathrm {KF}$
there will be a suitable
$\mathrm {KF}$
there will be a suitable
![]() $\mathrm {PKF}$
-style theory that has exactly the provably true sentences of the relevant
$\mathrm {PKF}$
-style theory that has exactly the provably true sentences of the relevant
![]() $\mathrm {KF}$
-style theory as theorems. Nicolai took these results to “partially [accomplish] a variant of a program sketched by Reinhardt” [Reference Nicolai14, p. 103].
$\mathrm {KF}$
-style theory as theorems. Nicolai took these results to “partially [accomplish] a variant of a program sketched by Reinhardt” [Reference Nicolai14, p. 103].
However, the work by Halbach and Nicolai provides at best a positive answer to Question (a). It does not—at least not immediately—yield an answer to Question (b). Indeed, it seems as if, despite working in a non-classical, two-sided sequent calculus, Halbach & Horsten [Reference Halbach and Horsten10] have largely neglected Question (b) of Reinhardt’s Challenge and so have subsequent publications on this issue. Indeed the version of
![]() $\mathrm {PKF}$
originally proposed by Halbach & Horsten [Reference Halbach and Horsten10] failed to yield a positive answer to Question (b) for rather banal reasons—even for theories with restricted induction: the version of
$\mathrm {PKF}$
originally proposed by Halbach & Horsten [Reference Halbach and Horsten10] failed to yield a positive answer to Question (b) for rather banal reasons—even for theories with restricted induction: the version of
![]() $\mathrm {KF}$
Halbach & Horsten [Reference Halbach and Horsten10] consider assumes the truth predicate to be consistent, which, as we shall explain in due course, means that the logic of KFSI is
$\mathrm {KF}$
Halbach & Horsten [Reference Halbach and Horsten10] consider assumes the truth predicate to be consistent, which, as we shall explain in due course, means that the logic of KFSI is
![]() ${\textsf {K}}\mathsf {3}$
. But Halbach and Horsten formulate
${\textsf {K}}\mathsf {3}$
. But Halbach and Horsten formulate
![]() $\mathrm {PKF}$
in symmetric strong Kleene logic
$\mathrm {PKF}$
in symmetric strong Kleene logic
![]() ${\textsf {KS}}\mathsf {3}$
and as a consequence
${\textsf {KS}}\mathsf {3}$
and as a consequence
![]() $\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner ,\mathrm{Tr}\ulcorner {\neg \varphi }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\psi }\urcorner $
while
$\mathrm {KF}\vdash \mathrm{Tr}\ulcorner {\varphi }\urcorner ,\mathrm{Tr}\ulcorner {\neg \varphi }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\psi }\urcorner $
while
![]() $\mathrm {PKF}\not \vdash \varphi ,\neg \varphi \Rightarrow \psi $
. The main technical contribution of this paper is to clarify the situation and to show how a positive answer to Question (b) of Reinhardt’s Challenge can be provided for
$\mathrm {PKF}\not \vdash \varphi ,\neg \varphi \Rightarrow \psi $
. The main technical contribution of this paper is to clarify the situation and to show how a positive answer to Question (b) of Reinhardt’s Challenge can be provided for
![]() $\mathrm {KF}$
-variants with restricted, or internal induction. To this end, we show how to pair the different variants of
$\mathrm {KF}$
-variants with restricted, or internal induction. To this end, we show how to pair the different variants of
![]() $\mathrm {KF}$
with a suitable
$\mathrm {KF}$
with a suitable
![]() $\mathrm {PKF}$
-style theory such that the provable sequents of the latter theory constitute exactly the significant inferences of the former theory. Moreover, it turns out that once we have an independent axiomatization of the set of significant inferences of the
$\mathrm {PKF}$
-style theory such that the provable sequents of the latter theory constitute exactly the significant inferences of the former theory. Moreover, it turns out that once we have an independent axiomatization of the set of significant inferences of the
![]() $\mathrm {KF}$
-variant under consideration, an affirmative answer to the Generalized Reinhardt Problem for the particular
$\mathrm {KF}$
-variant under consideration, an affirmative answer to the Generalized Reinhardt Problem for the particular
![]() $\mathrm {KF}$
-variant will be nothing but a corollary. What remains then to be shown to give a complete answer to the Generalized Reinhardt Problem and bring Reinhardt’s program to a successful completion is to show that
$\mathrm {KF}$
-variant will be nothing but a corollary. What remains then to be shown to give a complete answer to the Generalized Reinhardt Problem and bring Reinhardt’s program to a successful completion is to show that
![]() $\mathrm {PKF}^+$
—or, possibly, some other non-classical truth theory—amounts to a positive answer to Question (b) in the case of
$\mathrm {PKF}^+$
—or, possibly, some other non-classical truth theory—amounts to a positive answer to Question (b) in the case of
![]() $\mathrm {KF}$
with full induction. While to date we lack a proof to this effect, it seems very likely that our results can be extended to pair
$\mathrm {KF}$
with full induction. While to date we lack a proof to this effect, it seems very likely that our results can be extended to pair
![]() $\mathrm {KF}$
-variants with full induction with a suitable
$\mathrm {KF}$
-variants with full induction with a suitable
![]() $\mathrm {PKF}^+$
-theory.Footnote
12
This would show that
$\mathrm {PKF}^+$
-theory.Footnote
12
This would show that
![]() $\mathrm {PKF}^+$
amounts indeed to a positive answer to Question (b) for
$\mathrm {PKF}^+$
amounts indeed to a positive answer to Question (b) for
![]() $\mathrm {KF}$
with full induction and that Reinhardt’s program, on our proposed understanding, can be brought to a successful completion.Footnote
13
Indeed, the results for
$\mathrm {KF}$
with full induction and that Reinhardt’s program, on our proposed understanding, can be brought to a successful completion.Footnote
13
Indeed, the results for
![]() $\mathrm {KF}$
-variants with restricted or internal induction proved in this paper show that there is an alternative (and arguably more adequate) understanding of Reinhardt’s program. Taken together, these considerations shed new light on Reinhardt’s instrumentalism and vindicate Reinhardt’s optimism in regard to his program.
$\mathrm {KF}$
-variants with restricted or internal induction proved in this paper show that there is an alternative (and arguably more adequate) understanding of Reinhardt’s program. Taken together, these considerations shed new light on Reinhardt’s instrumentalism and vindicate Reinhardt’s optimism in regard to his program.
1.1 Plan of the paper
The paper starts by fixing some basic terminology and notation. More specifically, Section 2 introduces the language and the logical systems underlying
![]() $\mathrm {PKF}$
and its variants. That is, we introduce the logics
$\mathrm {PKF}$
and its variants. That is, we introduce the logics
![]() ${\textsf {FDE}}$
,
${\textsf {FDE}}$
,
![]() ${\textsf {KS}}\mathsf {3}$
,
${\textsf {KS}}\mathsf {3}$
,
![]() ${\textsf {K}}\mathsf {3}$
and
${\textsf {K}}\mathsf {3}$
and
![]() ${\textsf {LP}}$
. In the next section, Section 3, we introduce the relevant families of
${\textsf {LP}}$
. In the next section, Section 3, we introduce the relevant families of
![]() $\mathrm {KF}$
- and
$\mathrm {KF}$
- and
![]() $\mathrm {PKF}$
-like theories and observe some basic properties of these
$\mathrm {PKF}$
-like theories and observe some basic properties of these
![]() $\mathrm {PKF}$
-systems. In Section 4 we prove the central technical results of this paper. We show that for each
$\mathrm {PKF}$
-systems. In Section 4 we prove the central technical results of this paper. We show that for each
![]() $\mathrm {KF}$
-like theory with restricted or internal induction we can find a
$\mathrm {KF}$
-like theory with restricted or internal induction we can find a
![]() $\mathrm {PKF}$
-counterpart such that the latter is an independent axiomatization of the significant inferences of the former. In other words, we show that the set of pairs
$\mathrm {PKF}$
-counterpart such that the latter is an independent axiomatization of the significant inferences of the former. In other words, we show that the set of pairs
![]() $\langle {\Gamma , \Delta }\rangle $
such that
$\langle {\Gamma , \Delta }\rangle $
such that
![]() $\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
is derivable in a
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
is derivable in a
![]() $\mathrm {KF}$
-like theory coincides with the set of pairs
$\mathrm {KF}$
-like theory coincides with the set of pairs
![]() $\langle {\Gamma , \Delta }\rangle $
such that
$\langle {\Gamma , \Delta }\rangle $
such that
![]() $\Gamma \Rightarrow \Delta $
is derivable in a corresponding
$\Gamma \Rightarrow \Delta $
is derivable in a corresponding
![]() $\mathrm {PKF}$
-like theory. As mentioned, a positive answer to Generalized Reinhardt Problem is but an immediate corollary of the existence of such an independent axiomatization. In the conclusion (Section 5) we reevaluate Reinhardt’s program, that is, the prospect of an instrumentalist interpretation of
$\mathrm {PKF}$
-like theory. As mentioned, a positive answer to Generalized Reinhardt Problem is but an immediate corollary of the existence of such an independent axiomatization. In the conclusion (Section 5) we reevaluate Reinhardt’s program, that is, the prospect of an instrumentalist interpretation of
![]() $\mathrm {KF}$
in light of our technical results.
$\mathrm {KF}$
in light of our technical results.
2 Logics and formal notation
2.1 Language and notation
The language
![]() $\mathcal {L}_{\mathrm {PA}}$
denotes the language of first-order Peano arithmetic (
$\mathcal {L}_{\mathrm {PA}}$
denotes the language of first-order Peano arithmetic (
![]() $\mathrm {PA}$
) in the signature
$\mathrm {PA}$
) in the signature
![]() $\{\overline {0},',+,\times \}$
expanded by finitely many function symbols for suitable primitive recursive (p.r.) functions. The language
$\{\overline {0},',+,\times \}$
expanded by finitely many function symbols for suitable primitive recursive (p.r.) functions. The language
![]() $\mathcal {L}_{\mathrm{Tr}}^-$
expands
$\mathcal {L}_{\mathrm{Tr}}^-$
expands
![]() $\mathcal {L}_{\mathrm {PA}}$
by a unary truth-predicate
$\mathcal {L}_{\mathrm {PA}}$
by a unary truth-predicate
![]() $\mathrm{Tr}$
. Terms and formulae are generated by closing off under
$\mathrm{Tr}$
. Terms and formulae are generated by closing off under
![]() $\neg ,\land ,\forall $
(
$\neg ,\land ,\forall $
(
![]() $\lor ,\exists ,\rightarrow ,\leftrightarrow $
are defined according to the conventions of classical logic). By an
$\lor ,\exists ,\rightarrow ,\leftrightarrow $
are defined according to the conventions of classical logic). By an
![]() $\mathcal {L}_{\mathrm{Tr}}^{-}$
-expression we mean a term or a formula of
$\mathcal {L}_{\mathrm{Tr}}^{-}$
-expression we mean a term or a formula of
![]() $\mathcal {L}_{\mathrm{Tr}}^{-}$
. We let
$\mathcal {L}_{\mathrm{Tr}}^{-}$
. We let
![]() $\overline {n}$
be the numeral corresponding to the number
$\overline {n}$
be the numeral corresponding to the number
![]() $n\in \omega $
. We fix a canonical Gödel numbering of
$n\in \omega $
. We fix a canonical Gödel numbering of
![]() $\mathcal {L}_{\mathrm{Tr}}^{-}$
-expressions. If e is an
$\mathcal {L}_{\mathrm{Tr}}^{-}$
-expressions. If e is an
![]() $\mathcal {L}_{\mathrm{Tr}}^{-}$
-expression, the Gödel number (= gn) of e is denoted by
$\mathcal {L}_{\mathrm{Tr}}^{-}$
-expression, the Gödel number (= gn) of e is denoted by
![]() $\#e$
and
$\#e$
and
![]() $\ulcorner {e}\urcorner $
is the term representing
$\ulcorner {e}\urcorner $
is the term representing
![]() $\#e$
in
$\#e$
in
![]() $\mathcal {L}_{\mathrm {PA}}$
. The sets of terms, closed terms, variables, formulae, and sentences of
$\mathcal {L}_{\mathrm {PA}}$
. The sets of terms, closed terms, variables, formulae, and sentences of
![]() $\mathcal {L}_{\mathrm{Tr}}^-$
are p.r., and our language contains function symbols representing them. In practice, we take the following
$\mathcal {L}_{\mathrm{Tr}}^-$
are p.r., and our language contains function symbols representing them. In practice, we take the following
![]() $\mathcal {L}_{\mathrm{Tr}}^-$
-predicates to abbreviate the equations for the (p.r.) characteristic functions for such sets. For example,
$\mathcal {L}_{\mathrm{Tr}}^-$
-predicates to abbreviate the equations for the (p.r.) characteristic functions for such sets. For example,
![]() $\mathrm {Ct}({x})$
abbreviates
$\mathrm {Ct}({x})$
abbreviates
![]() $f_{\!\mathrm {Ct}}(x)=1$
, where
$f_{\!\mathrm {Ct}}(x)=1$
, where
![]() $f_{\!\mathrm {Ct}}$
is the characteristic function of the set of codes of closed terms:
$f_{\!\mathrm {Ct}}$
is the characteristic function of the set of codes of closed terms:
 $$ \begin{align*} &\mathrm{Tm}({x}) \ (\mathrm{Ct}({x})) := x \text{ is the gn of a (closed) term}; \\ &\mathrm{Var}({x}) := x \text{ is the gn of variable}; \\ &\mathrm{Fml}_{\mathrm{Tr}}^n(x) \ (\mathrm{St}_{\mathrm{Tr}}({x})) := x \text{ is the gn of a formula with at most } n \ (0) \text{ free distinct} \\ & \text{variables}; \\ &\mathrm{Eq}(x) := x \text{ is the gn of an equality between closed terms}; \\ &\mathrm{Ver}(x) := x \text{ is the gn of true closed equality}. \end{align*} $$
$$ \begin{align*} &\mathrm{Tm}({x}) \ (\mathrm{Ct}({x})) := x \text{ is the gn of a (closed) term}; \\ &\mathrm{Var}({x}) := x \text{ is the gn of variable}; \\ &\mathrm{Fml}_{\mathrm{Tr}}^n(x) \ (\mathrm{St}_{\mathrm{Tr}}({x})) := x \text{ is the gn of a formula with at most } n \ (0) \text{ free distinct} \\ & \text{variables}; \\ &\mathrm{Eq}(x) := x \text{ is the gn of an equality between closed terms}; \\ &\mathrm{Ver}(x) := x \text{ is the gn of true closed equality}. \end{align*} $$
Additionally,
![]() $\mathcal {L}_{\mathrm{Tr}}^{-}$
contains function symbols for the following p.r. operations on Gödel numbers:
$\mathcal {L}_{\mathrm{Tr}}^{-}$
contains function symbols for the following p.r. operations on Gödel numbers:

The expression
![]() $e[t/v_k]$
is the result of replacing, in the expression e, each free occurrence of
$e[t/v_k]$
is the result of replacing, in the expression e, each free occurrence of
![]() $v_k$
by the term t. Since
$v_k$
by the term t. Since
![]() $\mathcal {L}_{\mathrm{Tr}}^-$
contains only finitely many function symbols, there exists a p.r. evaluation function VAL on codes of closed terms of
$\mathcal {L}_{\mathrm{Tr}}^-$
contains only finitely many function symbols, there exists a p.r. evaluation function VAL on codes of closed terms of
![]() $\mathcal {L}_{\mathrm{Tr}}^-$
, such that
$\mathcal {L}_{\mathrm{Tr}}^-$
, such that
![]() $\mathrm {VAL}(\#t)\mapsto t^{\mathbb {N}}$
, where
$\mathrm {VAL}(\#t)\mapsto t^{\mathbb {N}}$
, where
![]() $t^{\mathbb {N}}$
is the value of the closed term t in the standard model. We let
$t^{\mathbb {N}}$
is the value of the closed term t in the standard model. We let
![]() $\mathcal {L}_{\mathrm{Tr}}$
be the language
$\mathcal {L}_{\mathrm{Tr}}$
be the language
![]() $\mathcal {L}_{\mathrm{Tr}}^-$
augmented by a unary function symbol
$\mathcal {L}_{\mathrm{Tr}}^-$
augmented by a unary function symbol
![]() $\mathrm {val}({x})$
, which represents VAL.Footnote
14
$\mathrm {val}({x})$
, which represents VAL.Footnote
14
We will make use of the following abbreviations:

When it is clear from the context which variable is being replaced, we write
![]() ${{\mathrm {sb}}(x,t)}$
instead of
${{\mathrm {sb}}(x,t)}$
instead of
![]() $\mathrm {sb}(x, t, v)$
. The abbreviation
$\mathrm {sb}(x, t, v)$
. The abbreviation
![]() $\ulcorner {\varphi (\dot x)}\urcorner $
extends to the case of multivariables in the obvious way, and we write
$\ulcorner {\varphi (\dot x)}\urcorner $
extends to the case of multivariables in the obvious way, and we write
![]() $\ulcorner {\varphi (\dot {\vec {x}})}\urcorner $
for
$\ulcorner {\varphi (\dot {\vec {x}})}\urcorner $
for
![]() $\ulcorner {\varphi (\dot {x_1}, \ldots , \dot {x_n})}\urcorner $
. The Gödel numbering is canonical, so in particular we require that the following are provable in (a fragment of)
$\ulcorner {\varphi (\dot {x_1}, \ldots , \dot {x_n})}\urcorner $
. The Gödel numbering is canonical, so in particular we require that the following are provable in (a fragment of)
![]() $\mathrm {PA}$
expanded by defining axioms for additional function symbols:
$\mathrm {PA}$
expanded by defining axioms for additional function symbols:

2.1.1 Terminology and notation for Gentzen-systems
A sequent is an expression of the form
![]() $\Gamma \Rightarrow \Delta $
, where
$\Gamma \Rightarrow \Delta $
, where
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
are finite sets of
$\Delta $
are finite sets of
![]() $\mathcal {L}_{\mathrm{Tr}}$
-formulae.
$\mathcal {L}_{\mathrm{Tr}}$
-formulae.
![]() $\Gamma $
is called the antecedent;
$\Gamma $
is called the antecedent;
![]() $\Delta $
is called the succedent. They are both referred to as cedents. Given a cedent
$\Delta $
is called the succedent. They are both referred to as cedents. Given a cedent
![]() $\Gamma :=\{\gamma _1, \ldots , \gamma _n\}$
, we set
$\Gamma :=\{\gamma _1, \ldots , \gamma _n\}$
, we set
![]() $\neg \Gamma :=\{\neg \gamma _i\mid \gamma _i\in \Gamma \}$
and
$\neg \Gamma :=\{\neg \gamma _i\mid \gamma _i\in \Gamma \}$
and
![]() $\mathrm{Tr}\ulcorner {\Gamma }\urcorner :=\{\mathrm{Tr}\ulcorner {\gamma }\urcorner \mid \gamma \in \Gamma \}$
. For t free for v in
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner :=\{\mathrm{Tr}\ulcorner {\gamma }\urcorner \mid \gamma \in \Gamma \}$
. For t free for v in
![]() $\Gamma $
(i.e., t is free for v for all members
$\Gamma $
(i.e., t is free for v for all members
![]() $\varphi _1, \ldots , \varphi _n$
of
$\varphi _1, \ldots , \varphi _n$
of
![]() $\Gamma $
), we write
$\Gamma $
), we write
![]() $\Gamma [t/v]$
for
$\Gamma [t/v]$
for
![]() $\{\varphi _1[t/v], \ldots , \varphi _n[t/v]\}$
.
$\{\varphi _1[t/v], \ldots , \varphi _n[t/v]\}$
.
A derivation of a sequent
![]() $\Gamma \Rightarrow \Delta $
is a tree with nodes labeled by sequents. The height of a derivation
$\Gamma \Rightarrow \Delta $
is a tree with nodes labeled by sequents. The height of a derivation
![]() $\mathcal {D}$
is the maximum length of the branches in the tree, where the length of a branch is the number of its nodes minus 1.
$\mathcal {D}$
is the maximum length of the branches in the tree, where the length of a branch is the number of its nodes minus 1.
In the rules of inference displayed below,
-
• formulae in
 $\Gamma , \Delta $
are called side formulae, or context,
$\Gamma , \Delta $
are called side formulae, or context, -
• the formulae not in the context in the conclusion are called principal formulae, and
-
• the formulae in the premises from which the conclusion is derived (i.e., the formulae in the premises not in the context) are called active formulae.
A literal is an atomic formula or the negation of an atomic formula. The cut rank of a formula which is eliminated in a cut-rule is the positive complexity of the formula. The supremum of the cut ranks of a derivation
![]() $\mathcal {D}$
is called the cut rank of
$\mathcal {D}$
is called the cut rank of
![]() $\mathcal {D}$
. The expression
$\mathcal {D}$
. The expression
![]() denotes that
denotes that
![]() $\Gamma \Rightarrow \Delta $
is derivable in S with a derivation of height
$\Gamma \Rightarrow \Delta $
is derivable in S with a derivation of height
![]() $\leq n$
and cut rank
$\leq n$
and cut rank
![]() $\leq m$
.
$\leq m$
.
2.2 Sequent calculi for
 ${\textsf {FDE}}$
and some of its extensions
${\textsf {FDE}}$
and some of its extensions
In this section we introduce the various logics underlying the systems of truth employed in the paper. We start with the two-sided sequent calculus of First Degree Entailment (
![]() ${\textsf {FDE}}$
). For a general overview of the different non-classical logics employed in this section see [Reference Priest19].
${\textsf {FDE}}$
). For a general overview of the different non-classical logics employed in this section see [Reference Priest19].
Definition 2.1 (
 ${\textsf {FDE}}$
).
${\textsf {FDE}}$
).
The logic of
![]() ${\textsf {FDE}}$
consists of the following axioms and rules.
${\textsf {FDE}}$
consists of the following axioms and rules.

Conditions of application:
![]() $\varphi $
literal in Ax; u eigenparameter.
$\varphi $
literal in Ax; u eigenparameter.
Remark 2.2. By means of a standard induction, one can show that the sequents
![]() $\varphi , \Gamma \Rightarrow \Delta , \varphi $
are derivable for all
$\varphi , \Gamma \Rightarrow \Delta , \varphi $
are derivable for all
![]() $\varphi \in \mathcal {L}_{\mathrm{Tr}}$
.
$\varphi \in \mathcal {L}_{\mathrm{Tr}}$
.
![]() ${\textsf {FDE}}$
is the base logic of
${\textsf {FDE}}$
is the base logic of
![]() $\mathrm {PKF}$
. Semantically, models of this logic admit both truth-value gluts (sentences which are both true and false) and truth-value gaps (sentences which are neither true nor false). Other
$\mathrm {PKF}$
. Semantically, models of this logic admit both truth-value gluts (sentences which are both true and false) and truth-value gaps (sentences which are neither true nor false). Other
![]() $\mathrm {PKF}$
-variants are based on extensions of
$\mathrm {PKF}$
-variants are based on extensions of
![]() ${\textsf {FDE}}$
, obtained by adding one additional rule which restricts the class of models. These additional rules are introduced below, and the extensions of
${\textsf {FDE}}$
, obtained by adding one additional rule which restricts the class of models. These additional rules are introduced below, and the extensions of
![]() ${\textsf {FDE}}$
are the defined in Definition 2.4.
${\textsf {FDE}}$
are the defined in Definition 2.4.
Definition 2.3. Let
![]() $\varphi $
be an atomic
$\varphi $
be an atomic
![]() $\mathcal {L}_{\mathrm{Tr}}$
-sentence. Then
$\mathcal {L}_{\mathrm{Tr}}$
-sentence. Then
The rule
![]() $\neg $
L (
$\neg $
L (
![]() $\neg $
R) restricts the class of models to those in which there is no glut (gap). The label GG stands for “gaps or gluts,” as via this rule we can derive
$\neg $
R) restricts the class of models to those in which there is no glut (gap). The label GG stands for “gaps or gluts,” as via this rule we can derive
![]() $\varphi , \neg \varphi , \Gamma \Rightarrow \Delta , \psi , \neg \psi $
, thereby excluding the simultaneous occurrence of gaps and gluts.Footnote
15
The
$\varphi , \neg \varphi , \Gamma \Rightarrow \Delta , \psi , \neg \psi $
, thereby excluding the simultaneous occurrence of gaps and gluts.Footnote
15
The
![]() ${\textsf {FDE}}$
extensions are then defined as follows:
${\textsf {FDE}}$
extensions are then defined as follows:
Definition 2.4 (Extensions of
 ${\textsf {FDE}}$
).
${\textsf {FDE}}$
).
-
• Classical Logic,
 ${\textsf {CL}}$
, is the system given by
${\textsf {CL}}$
, is the system given by
 ${\textsf {FDE}}$
without
${\textsf {FDE}}$
without
 $\neg \circ $
M, for
$\neg \circ $
M, for
 $\circ \in \{\neg , \land , \forall \}, M\in \{\mathrm {L}, \mathrm {R}\}$
, and with the addition of unrestricted
$\circ \in \{\neg , \land , \forall \}, M\in \{\mathrm {L}, \mathrm {R}\}$
, and with the addition of unrestricted
 $\neg $
L and
$\neg $
L and
 $\neg $
R.Footnote
16
$\neg $
R.Footnote
16
-
• Strong Kleene,
 ${\textsf {K}}\mathsf {3}$
, is the system
${\textsf {K}}\mathsf {3}$
, is the system
 ${\textsf {FDE}} + \neg \mathrm{L}$
.
${\textsf {FDE}} + \neg \mathrm{L}$
. -
• Logic of Paradox,
 ${\textsf {LP}}$
, is the system
${\textsf {LP}}$
, is the system
 ${\textsf {FDE}} \ + \neg \mathrm{R}$
.
${\textsf {FDE}} \ + \neg \mathrm{R}$
. -
• Kleene’s Symmetric Logic,
 ${\textsf {KS}}\mathsf {3}$
, is the system
${\textsf {KS}}\mathsf {3}$
, is the system
 ${\textsf {FDE}} + {{\rm GG}}$
.Footnote
17
${\textsf {FDE}} + {{\rm GG}}$
.Footnote
17
We now extend the base logics with rules for identity.
Definition 2.5 (Identity rules).
Let
![]() $\varphi $
be a literal. Then
$\varphi $
be a literal. Then

Each of the logic introduced in Definition 2.4 will now be extended with rules axiomatizing the identity predicate.
Definition 2.6 (Logics with identity).
We set
-
•
 ${\textsf {CL}}_{=}$
is
${\textsf {CL}}_{=}$
is
 ${\textsf {CL}} \ + \mathrm{Ref} + \mathrm{RepL}$
.
${\textsf {CL}} \ + \mathrm{Ref} + \mathrm{RepL}$
. -
•
 ${\textsf {FDE}}_{=}$
is
${\textsf {FDE}}_{=}$
is
 ${\textsf {FDE}} \ + \mathrm{Ref} + \mathrm{RepL}$
.
${\textsf {FDE}} \ + \mathrm{Ref} + \mathrm{RepL}$
. -
•
 ${\textsf {K}}\mathsf {3}_{=}$
is
${\textsf {K}}\mathsf {3}_{=}$
is
 ${\textsf {K}}\mathsf {3} + \mathrm{Ref} + \mathrm{RepL}$
.
${\textsf {K}}\mathsf {3} + \mathrm{Ref} + \mathrm{RepL}$
. -
•
 ${\textsf {LP}}_{=}$
is
${\textsf {LP}}_{=}$
is
 ${\textsf {LP}} + \mathrm{Ref} + \mathrm{RepR}$
.
${\textsf {LP}} + \mathrm{Ref} + \mathrm{RepR}$
. -
•
 ${\textsf {KS}}\mathsf {3}_{=}$
is
${\textsf {KS}}\mathsf {3}_{=}$
is
 ${\textsf {KS}}\mathsf {3} + \mathrm{Ref} + \mathrm{RepL}$
.
${\textsf {KS}}\mathsf {3} + \mathrm{Ref} + \mathrm{RepL}$
.
Remark 2.7.
-
• (RepL) and (RepR) are equivalent over
 ${\textsf {FDE}}$
, and they both yield the replacement schema for all
${\textsf {FDE}}$
, and they both yield the replacement schema for all $$\begin{align*}s = t, \varphi(s), \Gamma\Rightarrow\Delta, \varphi(t), \end{align*}$$
$$\begin{align*}s = t, \varphi(s), \Gamma\Rightarrow\Delta, \varphi(t), \end{align*}$$
 $\varphi \in \mathcal {L}_{\mathrm{Tr}}$
.
$\varphi \in \mathcal {L}_{\mathrm{Tr}}$
.
-
• The reason for formulating
 ${\textsf {K}}\mathsf {3}_=$
and
${\textsf {K}}\mathsf {3}_=$
and
 ${\textsf {KS}}\mathsf {3}_=$
with RepL, and
${\textsf {KS}}\mathsf {3}_=$
with RepL, and
 ${\textsf {LP}}$
with RepR, is to obtain a syntactic proof of full Cut elimination. Restrictions on
${\textsf {LP}}$
with RepR, is to obtain a syntactic proof of full Cut elimination. Restrictions on
 $\neg $
L,
$\neg $
L,
 $\neg $
R, and
$\neg $
R, and
 ${{\rm GG}}$
are justified in the same way.Footnote
18
Unrestricted versions of these rules can be shown to be admissible in the respective system by induction on the positive complexity on
${{\rm GG}}$
are justified in the same way.Footnote
18
Unrestricted versions of these rules can be shown to be admissible in the respective system by induction on the positive complexity on
 $\varphi $
.Footnote
19
$\varphi $
.Footnote
19
-
• It can easily be shown that
 ${\textsf {FDE}}$
(
${\textsf {FDE}}$
(
 ${\textsf {KS}}\mathsf {3}$
) and
${\textsf {KS}}\mathsf {3}$
) and
 ${\textsf {BDM}}$
(
${\textsf {BDM}}$
(
 ${\textsf {SDM}}$
), that is, the system(s) defined by Nicolai [Reference Nicolai14], are equivalent.Footnote
20
The system
${\textsf {SDM}}$
), that is, the system(s) defined by Nicolai [Reference Nicolai14], are equivalent.Footnote
20
The system
 ${\textsf {KS}}\mathsf {3}$
, however, has the advantage of enjoying a cut elimination theorem. Note, though, that the same does not hold for systems extended with identity, that is,
${\textsf {KS}}\mathsf {3}$
, however, has the advantage of enjoying a cut elimination theorem. Note, though, that the same does not hold for systems extended with identity, that is,
 ${\textsf {FDE}}_{=}$
(
${\textsf {FDE}}_{=}$
(
 ${\textsf {KS}}\mathsf {3}_{=}$
) and
${\textsf {KS}}\mathsf {3}_{=}$
) and
 ${\sf BDM}_{=}$
(
${\sf BDM}_{=}$
(
 ${\sf SDM}_{=}$
) are not equivalent. This is so because, via contraposition, identity behaves classically in
${\sf SDM}_{=}$
) are not equivalent. This is so because, via contraposition, identity behaves classically in
 ${\sf BDM}_{=}$
(
${\sf BDM}_{=}$
(
 ${\sf SDM}_{=}$
).
${\sf SDM}_{=}$
).
3
 $\mathrm {KF}$
-like and
$\mathrm {KF}$
-like and
 $\mathrm {PKF}$
-like theories
$\mathrm {PKF}$
-like theories
This section introduces the
![]() $\mathrm {KF}$
-like and
$\mathrm {KF}$
-like and
![]() $\mathrm {PKF}$
-like truth theories we are going to investigate. The theory
$\mathrm {PKF}$
-like truth theories we are going to investigate. The theory
![]() $\mathrm {KF}$
, developed by Feferman in the 1980s and published in [Reference Feferman6], has been studied extensively, e.g., by Reinhardt [Reference Reinhardt20, Reference Reinhardt21], McGee [Reference McGee13], and Cantini [Reference Cantini2, Reference Cantini3]. As mentioned in the Introduction, in this article we concentrate on
$\mathrm {KF}$
, developed by Feferman in the 1980s and published in [Reference Feferman6], has been studied extensively, e.g., by Reinhardt [Reference Reinhardt20, Reference Reinhardt21], McGee [Reference McGee13], and Cantini [Reference Cantini2, Reference Cantini3]. As mentioned in the Introduction, in this article we concentrate on
![]() $\mathrm {KF}$
-variants with induction restricted on the arithmetical vocabulary, and on
$\mathrm {KF}$
-variants with induction restricted on the arithmetical vocabulary, and on
![]() $\mathrm {KF}$
-variants with internal induction. These were both introduced by Cantini [Reference Cantini2]. The theory Partial Kripke–Feferman (
$\mathrm {KF}$
-variants with internal induction. These were both introduced by Cantini [Reference Cantini2]. The theory Partial Kripke–Feferman (
![]() $\mathrm {PKF}$
) may be seen as the non-classical counterpart to
$\mathrm {PKF}$
) may be seen as the non-classical counterpart to
![]() $\mathrm {KF}$
. It was developed by Halbach & Horsten [Reference Halbach and Horsten10], and variants of
$\mathrm {KF}$
. It was developed by Halbach & Horsten [Reference Halbach and Horsten10], and variants of
![]() $\mathrm {PKF}$
have been introduced and studied by, e.g., Halbach & Nicolai [Reference Halbach and Nicolai11], Nicolai [Reference Nicolai14], and Fischer & Gratzl [Reference Fischer and Gratzl7].Footnote
21
$\mathrm {PKF}$
have been introduced and studied by, e.g., Halbach & Nicolai [Reference Halbach and Nicolai11], Nicolai [Reference Nicolai14], and Fischer & Gratzl [Reference Fischer and Gratzl7].Footnote
21
We begin by introducing different rules of induction employed in the formulation of the theories. To this end we fix a standard notation system of ordinals up to
![]() $\Gamma _0$
.Footnote
22
We use
$\Gamma _0$
.Footnote
22
We use
![]() $a, b, c, \ldots $
to denote the code of our notation system whose value is
$a, b, c, \ldots $
to denote the code of our notation system whose value is
![]() $\alpha , \beta , \gamma , \ldots \in On$
(with the exception of
$\alpha , \beta , \gamma , \ldots \in On$
(with the exception of
![]() $\omega $
and
$\omega $
and
![]() $\varepsilon $
-numbers, for which we use the ordinals themselves), and we use
$\varepsilon $
-numbers, for which we use the ordinals themselves), and we use
![]() $\prec $
to denote a standard primitive recursive ordering defined on codes of ordinals. The expression
$\prec $
to denote a standard primitive recursive ordering defined on codes of ordinals. The expression
![]() $\forall z\prec y (\varphi [z/v])$
is short for
$\forall z\prec y (\varphi [z/v])$
is short for
![]() $\forall z (\neg (\mathrm {Ord}(z) \land \mathrm {Ord}(y) \land z\prec y) \lor \varphi [z/v])$
, where
$\forall z (\neg (\mathrm {Ord}(z) \land \mathrm {Ord}(y) \land z\prec y) \lor \varphi [z/v])$
, where
![]() $\mathrm {Ord}$
represents the set of codes of ordinals. For
$\mathrm {Ord}$
represents the set of codes of ordinals. For
![]() $\alpha <\Gamma _0$
and a formula
$\alpha <\Gamma _0$
and a formula
![]() $\varphi (v)\in \mathcal {L}_{\mathrm{Tr}}$
we let
$\varphi (v)\in \mathcal {L}_{\mathrm{Tr}}$
we let
![]() $\mathrm {TI}^{<\alpha }(\varphi )$
denote the schemata of transfinite induction up to any ordinal below
$\mathrm {TI}^{<\alpha }(\varphi )$
denote the schemata of transfinite induction up to any ordinal below
![]() $\alpha $
:
$\alpha $
:

for
![]() $\beta<\alpha$
and y eigenvariable.
$\beta<\alpha$
and y eigenvariable.
We are going to use three additional schemata of induction. First, we have full induction:

for
![]() $\varphi \in \mathcal {L}_{\mathrm{Tr}}$
and u eigenvariable. Second, we have internal induction:
$\varphi \in \mathcal {L}_{\mathrm{Tr}}$
and u eigenvariable. Second, we have internal induction:

for u eigenvariable. Third, we have restricted internal induction:

for
![]() $\varphi \in \mathcal {L}_{\mathrm {PA}}$
and u eigenvariable.
$\varphi \in \mathcal {L}_{\mathrm {PA}}$
and u eigenvariable.
We now introduce the basic truth principles employed in the systems of truth we discuss in the paper.
Definition 3.1 (Truth-axioms and truth rules).
The following are truth-theoretic initial sequents
![]() $($
or truth axioms
$($
or truth axioms
![]() $)$
. TrReg is often called regularity axiom .Footnote
23
$)$
. TrReg is often called regularity axiom .Footnote
23

The following rules are called truth rules:

Conditions of application: u eigenvariable.
We begin by introducing the relevant variants of
![]() $\mathrm {KF}$
, and we then define their non-classical counterparts, i.e., the
$\mathrm {KF}$
, and we then define their non-classical counterparts, i.e., the
![]() $\mathrm {PKF}$
-like systems.
$\mathrm {PKF}$
-like systems.
Definition 3.2 (
 $\mathrm {KF}$
).
$\mathrm {KF}$
).
![]() $\mathrm {KF}$
is obtained from
$\mathrm {KF}$
is obtained from
![]() ${\textsf {CL}}_=$
by adding initial sequents of
${\textsf {CL}}_=$
by adding initial sequents of
![]() $\mathrm {PA}$
(see [Reference Takeuti23, Definition 9.3]); defining axioms for additional function symbols;
$\mathrm {PA}$
(see [Reference Takeuti23, Definition 9.3]); defining axioms for additional function symbols;
![]() ${{\rm IND}};$
truth axioms and truth rules of Definition 3.1, except the initial sequents
${{\rm IND}};$
truth axioms and truth rules of Definition 3.1, except the initial sequents
![]() $\neg \mathrm{Tr}\neg $
.
$\neg \mathrm{Tr}\neg $
.
Definition 3.3 (
 $\mathrm {KF}$
-variants).
$\mathrm {KF}$
-variants).
-
(i)
 $\mathrm {KF}_{{{\rm cs}}}$
is obtained from
$\mathrm {KF}_{{{\rm cs}}}$
is obtained from
 $\mathrm {KF}$
by adding the initial sequent (Cons)
$\mathrm {KF}$
by adding the initial sequent (Cons)
-
(ii)
 $\mathrm {KF}_{{{\rm cp}}}$
is obtained from
$\mathrm {KF}_{{{\rm cp}}}$
is obtained from
 $\mathrm {KF}$
by adding (Comp)
$\mathrm {KF}$
by adding (Comp)
-
(iii)
 $\mathrm {KF}_{{{\rm S}}}$
is obtained from
$\mathrm {KF}_{{{\rm S}}}$
is obtained from
 $\mathrm {KF}$
by adding (GoG)
$\mathrm {KF}$
by adding (GoG)
For
![]() $\mathrm {KF}_\star \in \{\mathrm {KF}, \mathrm {KF}_{{{\rm cs}}}, \mathrm {KF}_{{{\rm cp}}}, \mathrm {KF}_{{{\rm S}}}\}$
,
$\mathrm {KF}_\star \in \{\mathrm {KF}, \mathrm {KF}_{{{\rm cs}}}, \mathrm {KF}_{{{\rm cp}}}, \mathrm {KF}_{{{\rm S}}}\}$
,
-
(iv)
 $\mathrm {KF}^-_\star $
is obtained from
$\mathrm {KF}^-_\star $
is obtained from
 $\mathrm {KF}_\star $
by replacing
$\mathrm {KF}_\star $
by replacing
 ${{\rm IND}}$
with
${{\rm IND}}$
with
 ${{\rm IND}}^{{{\rm int}}}_{\mathcal {L}_{\mathrm {PA}}}$
.
${{\rm IND}}^{{{\rm int}}}_{\mathcal {L}_{\mathrm {PA}}}$
. -
(v)
 $\mathrm {KF}^{{{\rm int}}}_\star $
is obtained from
$\mathrm {KF}^{{{\rm int}}}_\star $
is obtained from
 $\mathrm {KF}_\star $
by replacing
$\mathrm {KF}_\star $
by replacing
 ${{\rm IND}}$
with
${{\rm IND}}$
with
 ${{\rm IND}}^{{{\rm int}}}$
.
${{\rm IND}}^{{{\rm int}}}$
.
In what follows, theories introduced via items (iv) and (v) of Definition 3.3 will be referred to as
![]() $\mathrm {KF}$
-like theories (or systems) or as
$\mathrm {KF}$
-like theories (or systems) or as
![]() $\mathrm {KF}$
-variants.
$\mathrm {KF}$
-variants.
Remark 3.4. Let
![]() $\mathrm {KF}^\circ \in \{\mathrm {KF}^{{{\rm int}}},\mathrm {KF}^{{{\rm int}}}_{{{\rm cs}}},\mathrm {KF}^{{{\rm int}}}_{{{\rm cp}}},\mathrm {KF}^-,\mathrm {KF}^-_{{{\rm cs}}},\mathrm {KF}^-_{{{\rm cp}}}\}$
. Every axiom of
$\mathrm {KF}^\circ \in \{\mathrm {KF}^{{{\rm int}}},\mathrm {KF}^{{{\rm int}}}_{{{\rm cs}}},\mathrm {KF}^{{{\rm int}}}_{{{\rm cp}}},\mathrm {KF}^-,\mathrm {KF}^-_{{{\rm cs}}},\mathrm {KF}^-_{{{\rm cp}}}\}$
. Every axiom of
![]() $\mathrm {KF}^\circ $
has the form
$\mathrm {KF}^\circ $
has the form
![]() $\Theta , \Gamma \Rightarrow \Delta , \Lambda $
. Formulae in
$\Theta , \Gamma \Rightarrow \Delta , \Lambda $
. Formulae in
![]() $\Theta ,\Lambda $
are called active. Every active formula has positive complexity
$\Theta ,\Lambda $
are called active. Every active formula has positive complexity
![]() $0$
.
$0$
.
Let us remark that our formulation of
![]() $\mathrm {KF}^-_\star $
deviates from the standard formulation. Typically, the systems
$\mathrm {KF}^-_\star $
deviates from the standard formulation. Typically, the systems
![]() $\mathrm {KF}^-_\star $
are defined by restricting the induction schema
$\mathrm {KF}^-_\star $
are defined by restricting the induction schema
![]() ${{\rm IND}}$
to the arithmetical vocabulary, as, e.g., in [Reference Cantini2, Reference Halbach9]. The reason why we have introduced this different—yet equivalent, as shown in Observation 3.6—formulation is that our arguments below rely on partial Cut elimination, which fails in presence of induction, but which can be restored for
${{\rm IND}}$
to the arithmetical vocabulary, as, e.g., in [Reference Cantini2, Reference Halbach9]. The reason why we have introduced this different—yet equivalent, as shown in Observation 3.6—formulation is that our arguments below rely on partial Cut elimination, which fails in presence of induction, but which can be restored for
![]() $\mathrm {KF}$
-systems with internal induction, as well as for
$\mathrm {KF}$
-systems with internal induction, as well as for
![]() $\mathrm {KF}$
-systems with restricted internal induction.Footnote
25
In order to state this precisely, call a derivation
$\mathrm {KF}$
-systems with restricted internal induction.Footnote
25
In order to state this precisely, call a derivation
![]() $\mathcal {D}$
quasi-normal if
$\mathcal {D}$
quasi-normal if
![]() $\mathcal {D}$
has cut rank 0; then, by application of standard techniques for Cut elimination we obtain:
$\mathcal {D}$
has cut rank 0; then, by application of standard techniques for Cut elimination we obtain:
Proposition 3.5. Let
![]() $\mathrm {KF}^\circ \in \{\mathrm {KF}^{{{\rm int}}}_\star , \mathrm {KF}^-_\star \}$
, where
$\mathrm {KF}^\circ \in \{\mathrm {KF}^{{{\rm int}}}_\star , \mathrm {KF}^-_\star \}$
, where
![]() $\mathrm {KF}^{{{\rm int}}}_\star $
and
$\mathrm {KF}^{{{\rm int}}}_\star $
and
![]() $\mathrm {KF}^-_\star $
are as in Definition 3.3. Then every
$\mathrm {KF}^-_\star $
are as in Definition 3.3. Then every
![]() $\mathrm {KF}^\circ $
-derivation
$\mathrm {KF}^\circ $
-derivation
![]() $\mathcal {D}$
can be effectively transformed into a quasi-normal derivation
$\mathcal {D}$
can be effectively transformed into a quasi-normal derivation
![]() $\mathcal {D}'$
of the same end sequent.
$\mathcal {D}'$
of the same end sequent.
Observation 3.6. Let
![]() $\mathrm {KF}^{{{\rm int}}}_\star $
be as in Definition 3.3, and let
$\mathrm {KF}^{{{\rm int}}}_\star $
be as in Definition 3.3, and let
![]() $\mathrm {KF}_\star [{{\rm IND}}\negthickspace \upharpoonright \mathcal {L}_{\mathrm {PA}}]$
be the theory obtained from
$\mathrm {KF}_\star [{{\rm IND}}\negthickspace \upharpoonright \mathcal {L}_{\mathrm {PA}}]$
be the theory obtained from
![]() $\mathrm {KF}^{{{\rm int}}}_\star $
by replacing
$\mathrm {KF}^{{{\rm int}}}_\star $
by replacing
![]() ${{\rm IND}}^{{{\rm int}}}$
with the schema
${{\rm IND}}^{{{\rm int}}}$
with the schema
![]() ${{\rm IND}}$
restricted to
${{\rm IND}}$
restricted to
![]() $\mathcal {L}_{\mathrm {PA}}$
-sentences. Then
$\mathcal {L}_{\mathrm {PA}}$
-sentences. Then
![]() $\mathrm {KF}^-_\star $
and
$\mathrm {KF}^-_\star $
and
![]() $\mathrm {KF}_\star [{{\rm IND}}\negthickspace \upharpoonright \mathcal {L}_{\mathrm {PA}}]$
are equivalent.
$\mathrm {KF}_\star [{{\rm IND}}\negthickspace \upharpoonright \mathcal {L}_{\mathrm {PA}}]$
are equivalent.
Proof Idea.
Following [Reference Cantini2], one first shows that both
![]() $\mathrm {KF}_\star [{{\rm IND}}\negthickspace \upharpoonright \mathcal {L}_{\mathrm {PA}}]$
and
$\mathrm {KF}_\star [{{\rm IND}}\negthickspace \upharpoonright \mathcal {L}_{\mathrm {PA}}]$
and
![]() $\mathrm {KF}^-_\star $
prove the T-Schema on arithmetical formulae. That is to say one shows that both theories prove the sequents
$\mathrm {KF}^-_\star $
prove the T-Schema on arithmetical formulae. That is to say one shows that both theories prove the sequents
 $$ \begin{align*} \varphi(x), \Gamma&\Rightarrow\Delta , \mathrm{Tr}\ulcorner{\varphi(\dot x)}\urcorner, \\ \mathrm{Tr}\ulcorner{\varphi(\dot x)}\urcorner, \Gamma&\Rightarrow\Delta , \varphi(x), \end{align*} $$
$$ \begin{align*} \varphi(x), \Gamma&\Rightarrow\Delta , \mathrm{Tr}\ulcorner{\varphi(\dot x)}\urcorner, \\ \mathrm{Tr}\ulcorner{\varphi(\dot x)}\urcorner, \Gamma&\Rightarrow\Delta , \varphi(x), \end{align*} $$
if
![]() $\varphi $
does not contain
$\varphi $
does not contain
![]() $\mathrm{Tr}$
. The proof then continues by induction on the height of derivations. Since
$\mathrm{Tr}$
. The proof then continues by induction on the height of derivations. Since
![]() $\mathrm {KF}_\star [{{\rm IND}}\negthickspace \upharpoonright \mathcal {L}_{\mathrm {PA}}]$
and
$\mathrm {KF}_\star [{{\rm IND}}\negthickspace \upharpoonright \mathcal {L}_{\mathrm {PA}}]$
and
![]() $\mathrm {KF}^-_\star $
only differ for the employed induction schema, the just mentioned interderivability between
$\mathrm {KF}^-_\star $
only differ for the employed induction schema, the just mentioned interderivability between
![]() $\mathrm{Tr}\ulcorner {\varphi (\dot x)}\urcorner $
and
$\mathrm{Tr}\ulcorner {\varphi (\dot x)}\urcorner $
and
![]() $\varphi (x)$
immediately yields, via Cut, the desired conclusion.
$\varphi (x)$
immediately yields, via Cut, the desired conclusion.
We can now move on to
![]() $\mathrm {PKF}$
-like theories.
$\mathrm {PKF}$
-like theories.
Definition 3.7 (
 $\mathrm {PKF}$
).
$\mathrm {PKF}$
).
![]() $\mathrm {PKF}$
is obtained from
$\mathrm {PKF}$
is obtained from
![]() ${\textsf {FDE}}_=$
by adding: sequents
${\textsf {FDE}}_=$
by adding: sequents
![]() $\Gamma \Rightarrow \Delta $
for
$\Gamma \Rightarrow \Delta $
for
![]() $\Gamma \Rightarrow \Delta $
an initial sequent of
$\Gamma \Rightarrow \Delta $
an initial sequent of
![]() $\mathrm {PA}$
(see [Reference Takeuti23, Definition 9.3(1)]); defining axioms for additional function symbols;
$\mathrm {PA}$
(see [Reference Takeuti23, Definition 9.3(1)]); defining axioms for additional function symbols;
![]() ${{\rm IND}};$
truth axioms and truth rules of Definition 3.1; and the following two rules requiring identity statements to behave classically:
${{\rm IND}};$
truth axioms and truth rules of Definition 3.1; and the following two rules requiring identity statements to behave classically:
Definition 3.8 (
 $\mathrm {PKF}$
-variants).
$\mathrm {PKF}$
-variants).
We introduce variants of
![]() $\mathrm {PKF}$
$\mathrm {PKF}$
-
(i)
 $\mathrm {PKF}_{{{\rm cs}}}$
is obtained by adding
$\mathrm {PKF}_{{{\rm cs}}}$
is obtained by adding
 $\neg $
L to
$\neg $
L to
 $\mathrm {PKF}$
.
$\mathrm {PKF}$
. -
(ii)
 $\mathrm {PKF}_{{{\rm cp}}}$
is obtained by adding
$\mathrm {PKF}_{{{\rm cp}}}$
is obtained by adding
 $\neg $
R to
$\neg $
R to
 $\mathrm {PKF}$
.
$\mathrm {PKF}$
. -
(iii)
 $\mathrm {PKF}_{{{\rm S}}}$
is obtained by adding
$\mathrm {PKF}_{{{\rm S}}}$
is obtained by adding
 ${{\rm GG}}$
to
${{\rm GG}}$
to
 $\mathrm {PKF}$
.
$\mathrm {PKF}$
.
For
![]() $\mathrm {PKF}_\star \in \{\mathrm {PKF}, \mathrm {PKF}_{{{\rm cs}}}, \mathrm {PKF}_{{{\rm cp}}}, \mathrm {PKF}_{{{\rm S}}}\}$
,
$\mathrm {PKF}_\star \in \{\mathrm {PKF}, \mathrm {PKF}_{{{\rm cs}}}, \mathrm {PKF}_{{{\rm cp}}}, \mathrm {PKF}_{{{\rm S}}}\}$
,
-
(iv)
 $\mathrm {PKF}^-_\star $
is obtained by replacing
$\mathrm {PKF}^-_\star $
is obtained by replacing
 ${{\rm IND}}$
with
${{\rm IND}}$
with
 ${{\rm IND}}^{{{\rm int}}}_{\mathcal {L}_{\mathrm {PA}}}$
.
${{\rm IND}}^{{{\rm int}}}_{\mathcal {L}_{\mathrm {PA}}}$
. -
(v)
 $\mathrm {PKF}_\star ^+$
is obtained by extending
$\mathrm {PKF}_\star ^+$
is obtained by extending
 $\mathrm {PKF}_\star $
with
$\mathrm {PKF}_\star $
with
 $\mathrm {TI}^{<\varepsilon _0}$
.Footnote
26
$\mathrm {TI}^{<\varepsilon _0}$
.Footnote
26
Since our formulation of
![]() $\mathrm {PKF}$
deviates from the formulation in [Reference Halbach and Horsten10], we now show that
$\mathrm {PKF}$
deviates from the formulation in [Reference Halbach and Horsten10], we now show that
![]() $\mathrm {PKF}$
behaves classically on the
$\mathrm {PKF}$
behaves classically on the
![]() $\mathrm{Tr}$
-free fragment of
$\mathrm{Tr}$
-free fragment of
![]() $\mathcal {L}_{\mathrm{Tr}}$
and that
$\mathcal {L}_{\mathrm{Tr}}$
and that
![]() $\psi (\vec {x})$
and
$\psi (\vec {x})$
and
![]() $\mathrm{Tr}\ulcorner {\psi (\dot {\vec {x}})}\urcorner $
are interderivable.
$\mathrm{Tr}\ulcorner {\psi (\dot {\vec {x}})}\urcorner $
are interderivable.
Lemma 3.9. Let
![]() $\mathrm {PKF}^\circ $
be one of the
$\mathrm {PKF}^\circ $
be one of the
![]() $\mathrm {PKF}$
-like theories introduced in Definition 3.8,
$\mathrm {PKF}$
-like theories introduced in Definition 3.8,
![]() $\varphi \in \mathcal {L}_{\mathrm {PA}}$
, and
$\varphi \in \mathcal {L}_{\mathrm {PA}}$
, and
![]() $\psi (\vec {x})\in \mathcal {L}_{\mathrm{Tr}}$
. Then
$\psi (\vec {x})\in \mathcal {L}_{\mathrm{Tr}}$
. Then
-
(i)
 $\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta , \varphi , \neg \varphi $
and
$\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta , \varphi , \neg \varphi $
and
 $\mathrm {PKF}^\circ \vdash \varphi , \neg \varphi , \Gamma \Rightarrow \Delta ;$
$\mathrm {PKF}^\circ \vdash \varphi , \neg \varphi , \Gamma \Rightarrow \Delta ;$
-
(ii)
 $\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta , \psi (\vec {x})$
iff
$\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta , \psi (\vec {x})$
iff
 $\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta , \mathrm{Tr}\ulcorner {\psi (\dot {\vec {x}})}\urcorner ;$
$\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta , \mathrm{Tr}\ulcorner {\psi (\dot {\vec {x}})}\urcorner ;$
-
(iii) Unrestricted
 $\neg $
L and
$\neg $
L and
 $\neg $
R are admissible in
$\neg $
R are admissible in
 $\mathrm {PKF}^\circ $
for
$\mathrm {PKF}^\circ $
for
 $\varphi \in \mathcal {L}_{\mathrm {PA}}$
.
$\varphi \in \mathcal {L}_{\mathrm {PA}}$
.
Proof. (i) and (ii) are shown by a straightforward induction on
![]() $\varphi $
. For (iii), observe more generally that, if
$\varphi $
. For (iii), observe more generally that, if
![]() $\varphi , \neg \varphi , \Gamma \Rightarrow \Delta $
and
$\varphi , \neg \varphi , \Gamma \Rightarrow \Delta $
and
![]() $\Gamma \Rightarrow \Delta , \varphi , \neg \varphi $
are both derivable, then
$\Gamma \Rightarrow \Delta , \varphi , \neg \varphi $
are both derivable, then
![]() $\neg $
L and
$\neg $
L and
![]() $\neg $
R are derived rules
$\neg $
R are derived rules
Finally, to complete the picture we note that contraposition is admissible in
![]() $\mathrm {PKF}$
and
$\mathrm {PKF}$
and
![]() $\mathrm {PKF}_{{{\rm S}}}$
.
$\mathrm {PKF}_{{{\rm S}}}$
.
Lemma 3.10 (Contraposition).
Contraposition, i.e., the rule
is admissible in
![]() $\mathrm {PKF} (\mathrm {PKF}^-,\mathrm {PKF}^+)$
and
$\mathrm {PKF} (\mathrm {PKF}^-,\mathrm {PKF}^+)$
and
![]() $\mathrm {PKF}_{{{\rm S}}} (\mathrm {PKF}^-_{{{\rm S}}},\mathrm {PKF}^+_{{{\rm S}}})$
.
$\mathrm {PKF}_{{{\rm S}}} (\mathrm {PKF}^-_{{{\rm S}}},\mathrm {PKF}^+_{{{\rm S}}})$
.
Proof. The proof is by induction on the height of derivations. If
![]() $\Gamma \Rightarrow \Delta $
is an axiom of
$\Gamma \Rightarrow \Delta $
is an axiom of
![]() $\mathrm {PA}$
, the conclusion follows from Lemma 3.9(iii). For truth-theoretic initial sequents, the initial sequent
$\mathrm {PA}$
, the conclusion follows from Lemma 3.9(iii). For truth-theoretic initial sequents, the initial sequent
![]() $\neg \mathrm{Tr}\neg $
plays a central role. For derivations of height
$\neg \mathrm{Tr}\neg $
plays a central role. For derivations of height
![]() $>0$
, we show three crucial cases involving the rules
$>0$
, we show three crucial cases involving the rules
![]() ${{\rm GG}}$
, RepL, and IND. Suppose the derivation ends with
${{\rm GG}}$
, RepL, and IND. Suppose the derivation ends with

To begin with, using induction on
![]() $\mathcal {D}_{1}$
we first form
$\mathcal {D}_{1}$
we first form

We then continue as follows:

If the derivations ends with

we reason as follows. We first derive

If the derivation ends with

with u eigenvariable, we apply Parsons’ [Reference Parsons15] trick. By induction, we have
Replacing
![]() $t-(u+1)$
for u,
$t-(u+1)$
for u,
Since
![]() $(t-(u+1))+1 = t - u$
, by replacement of identicals we obtain
$(t-(u+1))+1 = t - u$
, by replacement of identicals we obtain
and hence by
![]() ${{\rm IND}}$
${{\rm IND}}$
 $$ \begin{gather*} \neg\varphi(t-\overline{0}), \neg\Gamma\Rightarrow\neg\Delta, \neg\varphi(t-t), \text{ i.e.,} \\ \neg\varphi(t), \neg\Gamma\Rightarrow\neg\Delta, \neg\varphi(\overline{0}). \\[-38pt] \end{gather*} $$
$$ \begin{gather*} \neg\varphi(t-\overline{0}), \neg\Gamma\Rightarrow\neg\Delta, \neg\varphi(t-t), \text{ i.e.,} \\ \neg\varphi(t), \neg\Gamma\Rightarrow\neg\Delta, \neg\varphi(\overline{0}). \\[-38pt] \end{gather*} $$
4 Reinhardt’s challenge
In this section we address Reinhardt’s Challenge and show that, given any
![]() $\mathrm {KF}$
-like theory with a restricted form of induction, there is a corresponding
$\mathrm {KF}$
-like theory with a restricted form of induction, there is a corresponding
![]() $\mathrm {PKF}$
-like theory such that the set of inferences
$\mathrm {PKF}$
-like theory such that the set of inferences
![]() $\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
provable in the
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
provable in the
![]() $\mathrm {PKF}$
-like theory coincides with the set of significant inferences of the
$\mathrm {PKF}$
-like theory coincides with the set of significant inferences of the
![]() $\mathrm {KF}$
-like theory. This observation may be considered as a positive answer to Question (b) discussed in the Introduction with respect to the particular
$\mathrm {KF}$
-like theory. This observation may be considered as a positive answer to Question (b) discussed in the Introduction with respect to the particular
![]() $\mathrm {KF}$
-like theories under consideration, that is, as providing an independent axiomatization of the significant inferences of the particular
$\mathrm {KF}$
-like theories under consideration, that is, as providing an independent axiomatization of the significant inferences of the particular
![]() $\mathrm {KF}$
-like theories. Moreover, by axiomatizing the set of significant inferences of these
$\mathrm {KF}$
-like theories. Moreover, by axiomatizing the set of significant inferences of these
![]() $\mathrm {KF}$
-like theories, we obtain a positive answer to the Generalized Reinhardt Problem as an immediate corollary. More precisely, we show in Proposition 4.11 that every significant inference of a
$\mathrm {KF}$
-like theories, we obtain a positive answer to the Generalized Reinhardt Problem as an immediate corollary. More precisely, we show in Proposition 4.11 that every significant inference of a
![]() $\mathrm {KF}$
-like theory with a restricted form of induction has a significant derivation, i.e., whenever the theory proves
$\mathrm {KF}$
-like theory with a restricted form of induction has a significant derivation, i.e., whenever the theory proves
![]() $\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
, we can find a derivation
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
, we can find a derivation
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
such that every node of
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
such that every node of
![]() $\mathcal {D}$
is itself a significant inference.
$\mathcal {D}$
is itself a significant inference.
To begin with, we introduce the notion of significant inference.
Definition 4.1 (Significant Inferences).
Let
![]() $\mathrm {Th}$
be an axiomatic truth theory formulated in
$\mathrm {Th}$
be an axiomatic truth theory formulated in
![]() $\mathcal {L}_{\mathrm{Tr}}$
, and
$\mathcal {L}_{\mathrm{Tr}}$
, and
![]() $\Gamma ,\Delta $
be finite sets of
$\Gamma ,\Delta $
be finite sets of
![]() $\mathcal {L}_{\mathrm{Tr}}$
-sentences. The set of significant inferences of
$\mathcal {L}_{\mathrm{Tr}}$
-sentences. The set of significant inferences of
![]() $\mathrm {Th}$
is defined as
$\mathrm {Th}$
is defined as
Since the truth predicate of
![]() $\mathrm {PKF}$
-like theories is transparent (cf. Lemma 3.9(ii)) the significant inferences of any
$\mathrm {PKF}$
-like theories is transparent (cf. Lemma 3.9(ii)) the significant inferences of any
![]() $\mathrm {PKF}$
-like theory will simply amount to the set of provable inferences of the theory. We also note in passing that the significant part of a truth theory (
$\mathrm {PKF}$
-like theory will simply amount to the set of provable inferences of the theory. We also note in passing that the significant part of a truth theory (
![]() $\mathrm {ThS}$
) in the sense of [Reference Reinhardt20, Reference Reinhardt21], that is the provably true sentences of the theory, can be retrieved from
$\mathrm {ThS}$
) in the sense of [Reference Reinhardt20, Reference Reinhardt21], that is the provably true sentences of the theory, can be retrieved from
![]() $\mathrm {ThSI}$
by setting
$\mathrm {ThSI}$
by setting
Let us now show that for every
![]() $\mathrm {KF}$
-like theory there is a
$\mathrm {KF}$
-like theory there is a
![]() $\mathrm {PKF}$
-like theory such that the provable sequents of the latter constitute exactly the significant inferences of the former.
$\mathrm {PKF}$
-like theory such that the provable sequents of the latter constitute exactly the significant inferences of the former.
Definition 4.2 (
 $\mathrm {PKF}^\circ , \mathrm {KF}^\circ $
).
$\mathrm {PKF}^\circ , \mathrm {KF}^\circ $
).
The pair
![]() $(\mathrm {PKF}^\circ , \mathrm {KF}^\circ )$
is a variable ranging over the following theory-pairs:
$(\mathrm {PKF}^\circ , \mathrm {KF}^\circ )$
is a variable ranging over the following theory-pairs:
 $$ \begin{gather*} (\mathrm{PKF}\negthickspace\upharpoonright, \mathrm{KF}\negthickspace\upharpoonright), (\mathrm{PKF}_{{{\rm cs}}}\negthickspace\upharpoonright, \mathrm{KF}_{{{\rm cs}}}\negthickspace\upharpoonright), (\mathrm{PKF}_{{{\rm cp}}}\negthickspace\upharpoonright, \mathrm{KF}_{{{\rm cp}}}\negthickspace\upharpoonright), (\mathrm{PKF}_{{{\rm S}}}\negthickspace\upharpoonright, \mathrm{KF}_{{{\rm S}}}\negthickspace\upharpoonright) \\ (\mathrm{PKF}, \mathrm{KF}^{{{\rm int}}}), (\mathrm{PKF}_{{{\rm cs}}}, \mathrm{KF}^{{{\rm int}}}_{{{\rm cs}}}), (\mathrm{PKF}_{{{\rm cp}}}, \mathrm{KF}^{{{\rm int}}}_{{{\rm cp}}}), (\mathrm{PKF}_{{{\rm S}}}, \mathrm{KF}^{{{\rm int}}}_{{{\rm S}}}). \end{gather*} $$
$$ \begin{gather*} (\mathrm{PKF}\negthickspace\upharpoonright, \mathrm{KF}\negthickspace\upharpoonright), (\mathrm{PKF}_{{{\rm cs}}}\negthickspace\upharpoonright, \mathrm{KF}_{{{\rm cs}}}\negthickspace\upharpoonright), (\mathrm{PKF}_{{{\rm cp}}}\negthickspace\upharpoonright, \mathrm{KF}_{{{\rm cp}}}\negthickspace\upharpoonright), (\mathrm{PKF}_{{{\rm S}}}\negthickspace\upharpoonright, \mathrm{KF}_{{{\rm S}}}\negthickspace\upharpoonright) \\ (\mathrm{PKF}, \mathrm{KF}^{{{\rm int}}}), (\mathrm{PKF}_{{{\rm cs}}}, \mathrm{KF}^{{{\rm int}}}_{{{\rm cs}}}), (\mathrm{PKF}_{{{\rm cp}}}, \mathrm{KF}^{{{\rm int}}}_{{{\rm cp}}}), (\mathrm{PKF}_{{{\rm S}}}, \mathrm{KF}^{{{\rm int}}}_{{{\rm S}}}). \end{gather*} $$
Moreover, let
![]() $\mathrm {Th}\in \{\mathrm {KF}^{{{\rm int}}},\mathrm {KF}\negthickspace \upharpoonright ,\mathrm {PKF}\negthickspace \upharpoonright \}$
. Then
$\mathrm {Th}\in \{\mathrm {KF}^{{{\rm int}}},\mathrm {KF}\negthickspace \upharpoonright ,\mathrm {PKF}\negthickspace \upharpoonright \}$
. Then
![]() $\mathrm {Th}_\star \in \{\mathrm {Th},\mathrm {Th}_{\mathrm {S}}, \mathrm {Th}_{\mathrm {cs}},\mathrm {Th}_{\mathrm {cp}}\}.$
$\mathrm {Th}_\star \in \{\mathrm {Th},\mathrm {Th}_{\mathrm {S}}, \mathrm {Th}_{\mathrm {cs}},\mathrm {Th}_{\mathrm {cp}}\}.$
Unless otherwise specified, we let
![]() $(\mathrm {PKF}^\circ ,\mathrm {KF}^\circ )$
be as in Definition 4.2.
$(\mathrm {PKF}^\circ ,\mathrm {KF}^\circ )$
be as in Definition 4.2.
We can now start proving the principal result of this section, i.e., we can prove that
![]() $\mathrm {PKF}^\circ =\mathrm {KF}^\circ \mathrm {SI}$
. We first show that
$\mathrm {PKF}^\circ =\mathrm {KF}^\circ \mathrm {SI}$
. We first show that
![]() $\mathrm {PKF}^\circ \subseteq \mathrm {KF}^\circ \mathrm {SI}$
.
$\mathrm {PKF}^\circ \subseteq \mathrm {KF}^\circ \mathrm {SI}$
.
Proposition 4.3. If
![]() $\mathrm {PKF}^\circ \vdash \Gamma (\vec {x})\Rightarrow \Delta (\vec {y})$
, then
$\mathrm {PKF}^\circ \vdash \Gamma (\vec {x})\Rightarrow \Delta (\vec {y})$
, then
![]() $\mathrm {KF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma (\dot {\vec {x}})}\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta (\dot {\vec {y}})}\urcorner $
.
$\mathrm {KF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma (\dot {\vec {x}})}\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta (\dot {\vec {y}})}\urcorner $
.
Proposition 4.3 is essentially due to Halbach & Horsten [Reference Halbach and Horsten10], Halbach & Nicolai [Reference Halbach and Nicolai11], and Nicolai [Reference Nicolai14], who proved the claim for theories without index cs or cp, that is, for pairs of theories that do not assume the truth predicate to be consistent or complete. It thus suffices to extend their result to these theories.
Proof of Proposition 4.3.
The proof is straightforward.Footnote
27
For pairs extended with a consistency principle, it suffices to show that the
![]() $\mathrm {KF}$
-theory “internalizes” the soundness of
$\mathrm {KF}$
-theory “internalizes” the soundness of
![]() $\neg $
L. That is, it suffices to show that, e.g., if
$\neg $
L. That is, it suffices to show that, e.g., if
![]() $\mathrm {KF}_{{{\rm cs}}}\vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner , \mathrm{Tr}\ulcorner {\varphi }\urcorner $
, then
$\mathrm {KF}_{{{\rm cs}}}\vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner , \mathrm{Tr}\ulcorner {\varphi }\urcorner $
, then
![]() $\mathrm {KF}_{{{\rm cs}}}\vdash \mathrm{Tr}\ulcorner {\neg \varphi }\urcorner , \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
. Symmetrically for theories extended with a completeness principle one needs to show that the
$\mathrm {KF}_{{{\rm cs}}}\vdash \mathrm{Tr}\ulcorner {\neg \varphi }\urcorner , \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
. Symmetrically for theories extended with a completeness principle one needs to show that the
![]() $\mathrm {KF}$
-theory “internalizes” the soundness of
$\mathrm {KF}$
-theory “internalizes” the soundness of
![]() $\neg $
R.
$\neg $
R.
In light of the definition of
![]() $\mathrm {KF}^\circ \mathrm {SI}$
, Proposition 4.3 immediately yields that the provable inferences of
$\mathrm {KF}^\circ \mathrm {SI}$
, Proposition 4.3 immediately yields that the provable inferences of
![]() $\mathrm {PKF}^\circ $
are a subset of
$\mathrm {PKF}^\circ $
are a subset of
![]() $\mathrm {KF}^\circ \mathrm {SI}$
:
$\mathrm {KF}^\circ \mathrm {SI}$
:
Corollary 4.4.
![]() $\mathrm {PKF}^\circ \subseteq \mathrm {KF}^\circ \mathrm {SI}$
.
$\mathrm {PKF}^\circ \subseteq \mathrm {KF}^\circ \mathrm {SI}$
.
4.1 From
 $\mathrm {KF}^\circ $
-significant inferences to
$\mathrm {KF}^\circ $
-significant inferences to
 $\mathrm {PKF}^\circ $
-provable sequents
$\mathrm {PKF}^\circ $
-provable sequents
The proof of the converse directions of Proposition 4.3 and Corollary 4.4 constitutes the main technical contribution of this article. The basic idea underlying the proof is to show that if
![]() $\mathrm {KF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
then
$\mathrm {KF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
then
![]() $\mathrm {PKF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
. This will be shown by proving a stronger claim, i.e., it will be shown that, whenever
$\mathrm {PKF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
. This will be shown by proving a stronger claim, i.e., it will be shown that, whenever
![]() $\Gamma , \Delta $
contain only literals, then
$\Gamma , \Delta $
contain only literals, then
where for a set of sentences
![]() $\Theta $
, and At the set of atomic sentences,
$\Theta $
, and At the set of atomic sentences,
This transformation is motivated by (i) the fact that identity behaves classically in
![]() $\mathrm {PKF}^\circ $
and (ii) the following semantic consideration: if a formula of the form
$\mathrm {PKF}^\circ $
and (ii) the following semantic consideration: if a formula of the form
![]() $\neg \mathrm{Tr}(t)$
is classically false (true), then
$\neg \mathrm{Tr}(t)$
is classically false (true), then
![]() $\mathrm{Tr}(t)$
is either true (false) or both (neither) from the perspective of the non-classical theory of truth. As a consequence, moving
$\mathrm{Tr}(t)$
is either true (false) or both (neither) from the perspective of the non-classical theory of truth. As a consequence, moving
![]() $\mathrm{Tr}(t)$
in the succedent (antecedent) of the sequent will not interfere with the validity of the sequent from the perspective of the non-classical logics at stake. Moreover, if
$\mathrm{Tr}(t)$
in the succedent (antecedent) of the sequent will not interfere with the validity of the sequent from the perspective of the non-classical logics at stake. Moreover, if
![]() $\Gamma \Rightarrow \Delta $
is of the form
$\Gamma \Rightarrow \Delta $
is of the form
![]() $\mathrm{Tr}\ulcorner {\Gamma '}\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta '}\urcorner $
, the transformation leaves the sequent unaltered; hence, if we prove that for each
$\mathrm{Tr}\ulcorner {\Gamma '}\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta '}\urcorner $
, the transformation leaves the sequent unaltered; hence, if we prove that for each
![]() $\mathrm {KF}^\circ $
-provable sequent its transformation is
$\mathrm {KF}^\circ $
-provable sequent its transformation is
![]() $\mathrm {PKF}^\circ $
-provable, we obtain our desired result as a corollary.
$\mathrm {PKF}^\circ $
-provable, we obtain our desired result as a corollary.
We first consider
![]() $\mathrm {KF}$
-systems with internal induction.
$\mathrm {KF}$
-systems with internal induction.
Lemma 4.5 (Main Lemma).
For
![]() $\Gamma , \Delta $
sets of literals, for all
$\Gamma , \Delta $
sets of literals, for all
![]() $\star $
$\star $
In the following proof, we implicitly use the fact that the replacement schema
![]() $s=t, \varphi (t), \Gamma \Rightarrow \Delta , \varphi (s)$
is derivable in each
$s=t, \varphi (t), \Gamma \Rightarrow \Delta , \varphi (s)$
is derivable in each
![]() $\mathrm {PKF}$
-like system of Definition 3.8. Also, let us recall that active formulae in truth-axioms and truth rules are literals.
$\mathrm {PKF}$
-like system of Definition 3.8. Also, let us recall that active formulae in truth-axioms and truth rules are literals.
Proof of Lemma 4.5.
The proof is by induction on the height n of
![]() $\mathrm {KF}^{{{\rm int}}}_\star $
-derivations. Suppose first that
$\mathrm {KF}^{{{\rm int}}}_\star $
-derivations. Suppose first that
![]() $n=0$
, and that
$n=0$
, and that
![]() $\Gamma \Rightarrow \Delta $
is a
$\Gamma \Rightarrow \Delta $
is a
![]() $\mathrm {KF}^{{{\rm int}}}_\star $
-initial sequent. For the pair
$\mathrm {KF}^{{{\rm int}}}_\star $
-initial sequent. For the pair
![]() $\mathrm {KF}^{{{\rm int}}}$
-
$\mathrm {KF}^{{{\rm int}}}$
-
![]() $\mathrm {PKF}$
, we first notice that every axiom of
$\mathrm {PKF}$
, we first notice that every axiom of
![]() $\mathrm {KF}^{{{\rm int}}}$
is an axiom of
$\mathrm {KF}^{{{\rm int}}}$
is an axiom of
![]() $\mathrm {PKF}$
. Hence for initial sequents not involving negated atomic formulae, the proof is immediate. The only truth-theoretic axiom of
$\mathrm {PKF}$
. Hence for initial sequents not involving negated atomic formulae, the proof is immediate. The only truth-theoretic axiom of
![]() $\mathrm {KF}^{{{\rm int}}}$
involving a negated atomic formula is
$\mathrm {KF}^{{{\rm int}}}$
involving a negated atomic formula is
![]() $\mathrm{Tr}{\neg }{=}$
. We obtain the desired conclusion by Lemma 3.9(iii), e.g., from
$\mathrm{Tr}{\neg }{=}$
. We obtain the desired conclusion by Lemma 3.9(iii), e.g., from
which is an initial sequent of
![]() $\mathrm {PKF}$
, via
$\mathrm {PKF}$
, via
![]() ${=}{\neg }$
R,
${=}{\neg }$
R,
![]() $\neg \neg $
L, and Cut, we can derive
$\neg \neg $
L, and Cut, we can derive
As for theories with specific
![]() $\mathrm{Tr}$
-axioms, we want to show that
$\mathrm{Tr}$
-axioms, we want to show that
![]() $\mathrm {PKF}_{{{\rm cp}}}$
,
$\mathrm {PKF}_{{{\rm cp}}}$
,
![]() $\mathrm {PKF}_{{{\rm cs}}}$
, and
$\mathrm {PKF}_{{{\rm cs}}}$
, and
![]() $\mathrm {PKF}_{{{\rm S}}}$
derive, respectively, the transformation of
$\mathrm {PKF}_{{{\rm S}}}$
derive, respectively, the transformation of
![]() ${{\rm Cons}}$
,
${{\rm Cons}}$
,
![]() ${{\rm Comp}}$
, and
${{\rm Comp}}$
, and
![]() ${{\rm GoG}}$
. That is to say, we have to show (we omit context for readability)
${{\rm GoG}}$
. That is to say, we have to show (we omit context for readability)
For (1)

For (2) we have

Finally, for (3)

In the last inference we have been sloppy. The double line indicates that from the upper sequent we can derive the lower sequent via some obvious additional steps involving the truth-theoretic initial sequents
![]() $\neg \mathrm{Tr}\neg \mathrm{Tr}$
and Cut.
$\neg \mathrm{Tr}\neg \mathrm{Tr}$
and Cut.
Now suppose that
![]() $n=m+1$
and that
$n=m+1$
and that
![]() $\Gamma \Rightarrow \Delta $
has been derived. We distinguish two cases:
$\Gamma \Rightarrow \Delta $
has been derived. We distinguish two cases:
Case 1:
![]() $\Gamma \Rightarrow \Delta $
contains no principal formula. In this case, the last inference of the derivation of
$\Gamma \Rightarrow \Delta $
contains no principal formula. In this case, the last inference of the derivation of
![]() $\Gamma \Rightarrow \Delta $
must be either Ref or Cut. If the former, we obtain our desired conclusion by i.h. and Ref in
$\Gamma \Rightarrow \Delta $
must be either Ref or Cut. If the former, we obtain our desired conclusion by i.h. and Ref in
![]() $\mathrm {PKF}_\star $
. Otherwise, the derivation ends with
$\mathrm {PKF}_\star $
. Otherwise, the derivation ends with

For this to work, it is crucial that we are dealing with quasi-normal derivations. In this case, we can assume the cut formula to be a literal and thus apply i.h. and Cut on
![]() $\mathrm {PKF}_\star $
. For example, if
$\mathrm {PKF}_\star $
. For example, if
![]() $\varphi \equiv \neg \psi $
for
$\varphi \equiv \neg \psi $
for
![]() $\psi \in \mathrm {At}$
, then we reason as follows:
$\psi \in \mathrm {At}$
, then we reason as follows:

If
![]() $\varphi \in {\rm At}$
, then we use i.h. and cut on
$\varphi \in {\rm At}$
, then we use i.h. and cut on
![]() $\varphi $
.
$\varphi $
.
Case 2:
![]() $\Gamma \Rightarrow \Delta $
contains a principal formula. We reason by subcases, according to the last inference of the derivation. Logical rules for
$\Gamma \Rightarrow \Delta $
contains a principal formula. We reason by subcases, according to the last inference of the derivation. Logical rules for
![]() $\land $
and
$\land $
and
![]() $\forall $
need not be taken into account as they cannot be the last rule of a quasi-normal derivation
$\forall $
need not be taken into account as they cannot be the last rule of a quasi-normal derivation
![]() $\mathcal {D}$
that has only literals in the end-sequent. The rules having literals as principal formulae are the following:
$\mathcal {D}$
that has only literals in the end-sequent. The rules having literals as principal formulae are the following:
![]() $\neg $
L,
$\neg $
L,
![]() $\neg $
R, RepL,
$\neg $
R, RepL,
![]() ${{\rm IND}}^{{{\rm int}}}$
, and truth rules.
${{\rm IND}}^{{{\rm int}}}$
, and truth rules.
Case 2.1: The last inference is
![]() $\neg $
L or
$\neg $
L or
![]() $\neg $
R. Here the conclusion is immediate, e.g., suppose the
$\neg $
R. Here the conclusion is immediate, e.g., suppose the
![]() $\mathrm {KF}^{{{\rm int}}}_\star $
-derivation ends with
$\mathrm {KF}^{{{\rm int}}}_\star $
-derivation ends with

If
![]() $\varphi \in {\rm At}$
, then by induction we have
$\varphi \in {\rm At}$
, then by induction we have
![]() $\mathrm {PKF}_\star \vdash \Gamma ^{\prime +}, \Delta ^-\Rightarrow \Gamma ^{\prime -}, \Delta ^+, \varphi $
, which is our desired conclusion. The case where
$\mathrm {PKF}_\star \vdash \Gamma ^{\prime +}, \Delta ^-\Rightarrow \Gamma ^{\prime -}, \Delta ^+, \varphi $
, which is our desired conclusion. The case where
![]() $\varphi \equiv \neg \psi $
for
$\varphi \equiv \neg \psi $
for
![]() $\psi $
atomic need not be taken into account, as we are dealing with derivations containing only literals in the end-sequent.
$\psi $
atomic need not be taken into account, as we are dealing with derivations containing only literals in the end-sequent.
Case 2.2: The last inference is RepL. Suppose the
![]() $\mathrm {KF}^{{{\rm int}}}_\star $
-derivation ends with
$\mathrm {KF}^{{{\rm int}}}_\star $
-derivation ends with

Assume first
![]() $\varphi \in {\rm At}$
. For the pairs
$\varphi \in {\rm At}$
. For the pairs
![]() $\mathrm {KF}^{{{\rm int}}}$
-
$\mathrm {KF}^{{{\rm int}}}$
-
![]() $\mathrm {PKF}$
,
$\mathrm {PKF}$
,
![]() $\mathrm {KF}^{{{\rm int}}}_{{{\rm cs}}}$
-
$\mathrm {KF}^{{{\rm int}}}_{{{\rm cs}}}$
-
![]() $\mathrm {PKF}_{{{\rm cs}}}$
, and
$\mathrm {PKF}_{{{\rm cs}}}$
, and
![]() $\mathrm {KF}^{{{\rm int}}}_{{{\rm S}}}$
-
$\mathrm {KF}^{{{\rm int}}}_{{{\rm S}}}$
-
![]() $\mathrm {PKF}_{{{\rm S}}}$
, we just apply i.h. and RepL in each
$\mathrm {PKF}_{{{\rm S}}}$
, we just apply i.h. and RepL in each
![]() $\mathrm {PKF}$
-variant. For the pair
$\mathrm {PKF}$
-variant. For the pair
![]() $\mathrm {KF}^{{{\rm int}}}_{{{\rm cp}}}$
-
$\mathrm {KF}^{{{\rm int}}}_{{{\rm cp}}}$
-
![]() $\mathrm {PKF}_{{{\rm cp}}}$
, since
$\mathrm {PKF}_{{{\rm cp}}}$
, since
![]() $\mathrm {PKF}_{{{\rm cp}}}$
does not have RepL, but RepR instead, we reason in
$\mathrm {PKF}_{{{\rm cp}}}$
does not have RepL, but RepR instead, we reason in
![]() $\mathrm {PKF}_{{{\rm cp}}}$
as follows, omitting context for readability:Footnote
29
$\mathrm {PKF}_{{{\rm cp}}}$
as follows, omitting context for readability:Footnote
29

For
![]() $\varphi \equiv \neg \psi $
with
$\varphi \equiv \neg \psi $
with
![]() $\psi $
atomic, we reason in an arbitrary
$\psi $
atomic, we reason in an arbitrary
![]() $\mathrm {PKF}_\star $
:
$\mathrm {PKF}_\star $
:

Case 2.3: The last inference is
![]() ${{\rm IND}}^{{{\rm int}}}$
. Suppose the
${{\rm IND}}^{{{\rm int}}}$
. Suppose the
![]() $\mathrm {KF}^{{{\rm int}}}_\star $
-derivation ends with
$\mathrm {KF}^{{{\rm int}}}_\star $
-derivation ends with

with u eigenvariable. We use
![]() ${{\rm IND}}$
in
${{\rm IND}}$
in
![]() $\mathrm {PKF}_\star $
as follows:
$\mathrm {PKF}_\star $
as follows:

Case 2.4: The last inference is a truth-rule. Finally, suppose the derivation ends with an application of a truth-rule. In this case, it essentially suffices to notice that each active formula of each truth-rule is an atomic formula. Hence, the desired conclusion follows by i.h. and the rule itself in
![]() $\mathrm {PKF}_\star $
. As an example, we consider the truth-rule
$\mathrm {PKF}_\star $
. As an example, we consider the truth-rule
![]() $\mathrm{Tr}\forall $
R. So suppose the derivation ends with
$\mathrm{Tr}\forall $
R. So suppose the derivation ends with

The conclusion follows immediately by i.h., i.e., we reason in
![]() $\mathrm {PKF}_\star $
as follows:
$\mathrm {PKF}_\star $
as follows:

By inspecting the proof of the Main Lemma, it can be observed that we can immediately lift it to the pair (
![]() $\mathrm {KF}^-_\star $
,
$\mathrm {KF}^-_\star $
,
![]() $\mathrm {PKF}^-_\star $
), thus obtaining the following.
$\mathrm {PKF}^-_\star $
), thus obtaining the following.
Corollary 4.6. For
![]() $\Gamma , \Delta $
sets of literals, for all
$\Gamma , \Delta $
sets of literals, for all
![]() $\star $
$\star $
This immediately yields that the set of significant inferences of
![]() $\mathrm {KF}$
-like theories is contained in the set of provable sequents of appropriate
$\mathrm {KF}$
-like theories is contained in the set of provable sequents of appropriate
![]() $\mathrm {PKF}$
-like theories.
$\mathrm {PKF}$
-like theories.
Lemma 4.7.
![]() $\mathrm {KF}^\circ \mathrm {SI}\subseteq \mathrm {PKF}^\circ $
.
$\mathrm {KF}^\circ \mathrm {SI}\subseteq \mathrm {PKF}^\circ $
.
Proof. If
![]() $\mathrm {KF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
, then
$\mathrm {KF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
, then
![]() $\mathrm {PKF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
by Lemma 4.5 and Corollary 4.6. But the truth predicate of
$\mathrm {PKF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
by Lemma 4.5 and Corollary 4.6. But the truth predicate of
![]() $\mathrm {PKF}^\circ $
is transparent and thus
$\mathrm {PKF}^\circ $
is transparent and thus
![]() $\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta $
.
$\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta $
.
Lemma 4.7 along with Corollary 4.4 shows that
![]() $\mathrm {PKF}^\circ $
yields precisely the significant sentence of
$\mathrm {PKF}^\circ $
yields precisely the significant sentence of
![]() $\mathrm {KF}^\circ $
. In other words we have answered Question (b) of Reinhardt’s Challenge.
$\mathrm {KF}^\circ $
. In other words we have answered Question (b) of Reinhardt’s Challenge.
Theorem 4.8 (Reinhardt’s Challenge).
![]() $\mathrm {PKF}^\circ = \mathrm {KF}^\circ \mathrm {SI}$
.
$\mathrm {PKF}^\circ = \mathrm {KF}^\circ \mathrm {SI}$
.
We remark that an answer to Reinhardt’s Question (b) yields an answer to Question (a) as a corollary, that is, our result subsumes parts of the results provided by Halbach & Horsten [Reference Halbach and Horsten10], Halbach & Nicolai [Reference Halbach and Nicolai11], and Nicolai Reference Nicolai14].
Corollary 4.9.
![]() $\{\varphi \in {{\rm Sent}}_{\mathcal {L}_{\mathrm{Tr}}}\mid \mathrm {PKF}^\circ \vdash \varphi \}=\mathrm {KF}^\circ \mathrm {S}$
.
$\{\varphi \in {{\rm Sent}}_{\mathcal {L}_{\mathrm{Tr}}}\mid \mathrm {PKF}^\circ \vdash \varphi \}=\mathrm {KF}^\circ \mathrm {S}$
.
Of course, this result also implies that, by means of a very simple observation connecting provably true
![]() $\mathrm {KF}$
-sequents to provable
$\mathrm {KF}$
-sequents to provable
![]() $\mathrm {PKF}$
-sequents, we have reduced questions regarding the proof-theoretic strength of
$\mathrm {PKF}$
-sequents, we have reduced questions regarding the proof-theoretic strength of
![]() $\mathrm {PKF}$
-like theories to questions regarding the proof-theoretic strength of
$\mathrm {PKF}$
-like theories to questions regarding the proof-theoretic strength of
![]() $\mathrm {KF}$
-like theories.
$\mathrm {KF}$
-like theories.
Corollary 4.10.
![]() $\mathrm {KF}^\circ $
and
$\mathrm {KF}^\circ $
and
![]() $\mathrm {PKF}^\circ $
are proof-theoretically equivalent, i.e.,
$\mathrm {PKF}^\circ $
are proof-theoretically equivalent, i.e.,
Concluding, we promised to give a positive answer to the Generalized Reinhardt Problem for
![]() $\mathrm {KF}$
-variants with restricted forms of induction, that is, the question whether for any pair
$\mathrm {KF}$
-variants with restricted forms of induction, that is, the question whether for any pair
![]() $\langle {\Gamma , \Delta }\rangle \in \mathrm {KF}^\circ \mathrm {SI}$
there is a
$\langle {\Gamma , \Delta }\rangle \in \mathrm {KF}^\circ \mathrm {SI}$
there is a
![]() $\mathrm {KF}^\circ $
-derivation such that each node of the derivation is a member of
$\mathrm {KF}^\circ $
-derivation such that each node of the derivation is a member of
![]() $\mathrm {KF}^\circ \mathrm {SI}$
. However, as anticipated in the Introduction (Section 1) to this paper, a positive answer to Generalized Reinhardt Problem follows rather immediately, once we have an independent axiomatization of
$\mathrm {KF}^\circ \mathrm {SI}$
. However, as anticipated in the Introduction (Section 1) to this paper, a positive answer to Generalized Reinhardt Problem follows rather immediately, once we have an independent axiomatization of
![]() $\mathrm {KF}^\circ \mathrm {SI}$
:
$\mathrm {KF}^\circ \mathrm {SI}$
:
Corollary 4.11 (Generalized Reinhardt Problem).
If
![]() $\langle {\Gamma , \Delta }\rangle \in \mathrm {KF}^\circ \mathrm {SI}$
, then there is a
$\langle {\Gamma , \Delta }\rangle \in \mathrm {KF}^\circ \mathrm {SI}$
, then there is a
![]() $\mathrm {KF}^\circ $
-derivation
$\mathrm {KF}^\circ $
-derivation
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $\Gamma \Rightarrow \Delta $
such that for each node d of
$\Gamma \Rightarrow \Delta $
such that for each node d of
![]() $\mathcal {D}$
,
$\mathcal {D}$
,
![]() $d\in \mathrm {KF}^\circ \mathrm {SI}$
.
$d\in \mathrm {KF}^\circ \mathrm {SI}$
.
Proof. If
![]() $\langle {\Gamma , \Delta }\rangle \in \mathrm {KF}^\circ \mathrm {SI}$
, then by Proposition 4.8
$\langle {\Gamma , \Delta }\rangle \in \mathrm {KF}^\circ \mathrm {SI}$
, then by Proposition 4.8
![]() $\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta $
and hence
$\mathrm {PKF}^\circ \vdash \Gamma \Rightarrow \Delta $
and hence
![]() $\mathrm {PKF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
. Now let
$\mathrm {PKF}^\circ \vdash \mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
. Now let
![]() $\mathcal {D}'$
be an arbitrary
$\mathcal {D}'$
be an arbitrary
![]() $\mathrm {KF}^\circ $
-derivation of
$\mathrm {KF}^\circ $
-derivation of
![]() $\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
.
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
.
In order to obtain our desired derivation
![]() $\mathcal {D}$
, it suffices to replace each node (including the leaves)
$\mathcal {D}$
, it suffices to replace each node (including the leaves)
of
![]() $\mathcal {D}'$
by
$\mathcal {D}'$
by
Let
![]() $\mathcal {D}$
be the derivation resulting from this transformation. Since
$\mathcal {D}$
be the derivation resulting from this transformation. Since
![]() $\mathrm {KF}^\circ $
is closed under weakening,
$\mathrm {KF}^\circ $
is closed under weakening,
![]() $\mathcal {D}$
is a
$\mathcal {D}$
is a
![]() $\mathrm {KF}^\circ $
-derivation of
$\mathrm {KF}^\circ $
-derivation of
![]() $\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
. But each node of
$\mathrm{Tr}\ulcorner {\Gamma }\urcorner \Rightarrow \mathrm{Tr}\ulcorner {\Delta }\urcorner $
. But each node of
![]() $\mathcal {D}$
is also derivable in
$\mathcal {D}$
is also derivable in
![]() $\mathrm {PKF}^\circ $
, too, since
$\mathrm {PKF}^\circ $
, too, since
![]() $\mathrm {PKF}^\circ $
is closed under weakening. Hence every node of
$\mathrm {PKF}^\circ $
is closed under weakening. Hence every node of
![]() $\mathcal {D}$
is in
$\mathcal {D}$
is in
![]() $\mathrm {PKF}^\circ =\mathrm {KF}^\circ \mathrm {SI}$
.
$\mathrm {PKF}^\circ =\mathrm {KF}^\circ \mathrm {SI}$
.
Let us put our partial answer to the Generalized Reinhardt Problem in perspective: we have shown that for every significant inference there is a way to classically derive the sequent such that every node of the derivation is itself a significant inference and hence that every node of the proof is acceptable to the significant reasoner, i.e., the non-classical logician. This does not imply that the non-classical logician can follow the classical reasoning, i.e., that the
![]() $\mathrm {KF}^\circ $
-proof is also a
$\mathrm {KF}^\circ $
-proof is also a
![]() $\mathrm {PKF}^\circ $
-proof. Our result only shows that
$\mathrm {PKF}^\circ $
-proof. Our result only shows that
![]() $\mathrm {KF}$
-style theories with restricted forms of induction can be used instrumentally. It does not show that one can always reason non-classically within
$\mathrm {KF}$
-style theories with restricted forms of induction can be used instrumentally. It does not show that one can always reason non-classically within
![]() $\mathrm {KF}^\circ $
. But if the latter were the case, it seems that
$\mathrm {KF}^\circ $
. But if the latter were the case, it seems that
![]() $\mathrm {KF}^\circ $
would deliver an independent axiomatization of its significant part in its own right.Footnote
30
Surely—while it is certainly an interesting question whether for every
$\mathrm {KF}^\circ $
would deliver an independent axiomatization of its significant part in its own right.Footnote
30
Surely—while it is certainly an interesting question whether for every
![]() $\mathrm {KF}^\circ $
-significant inference there is a
$\mathrm {KF}^\circ $
-significant inference there is a
![]() $\mathrm {KF}^\circ $
-derivation, which is also a
$\mathrm {KF}^\circ $
-derivation, which is also a
![]() $\mathrm {PKF}^\circ $
-derivation—such a result is not required for an instrumental interpretation of
$\mathrm {PKF}^\circ $
-derivation—such a result is not required for an instrumental interpretation of
![]() $\mathrm {KF}^\circ $
and left for future research.
$\mathrm {KF}^\circ $
and left for future research.
5 Conclusion
In this paper, we had a fresh look at Reinhardt’s program and we proposed to focus on the provably true inferences of
![]() $\mathrm {KF}$
-like theories rather than on the provably true sentences only. We showed that if we conceive of the significant part of
$\mathrm {KF}$
-like theories rather than on the provably true sentences only. We showed that if we conceive of the significant part of
![]() $\mathrm {KF}$
-like theories as the set of provably true inferences, then Reinhardt’s program can be deemed successful for variants of
$\mathrm {KF}$
-like theories as the set of provably true inferences, then Reinhardt’s program can be deemed successful for variants of
![]() $\mathrm {KF}$
with a restricted form of induction: we can remain within the significant part of the theories in proving their significant inferences. This answers the Generalized Reinhardt Problem for the aforementioned
$\mathrm {KF}$
with a restricted form of induction: we can remain within the significant part of the theories in proving their significant inferences. This answers the Generalized Reinhardt Problem for the aforementioned
![]() $\mathrm {KF}$
-variants and also shows that we need not step outside the significant part in proving theorems of the form
$\mathrm {KF}$
-variants and also shows that we need not step outside the significant part in proving theorems of the form
![]() $\mathrm{Tr}\ulcorner {\varphi }\urcorner $
, which was the content of the original formulation of Reinhardt’s Problem. The use of the nonsignificant part of
$\mathrm{Tr}\ulcorner {\varphi }\urcorner $
, which was the content of the original formulation of Reinhardt’s Problem. The use of the nonsignificant part of
![]() $\mathrm {KF}^{{{\rm int}}}$
and
$\mathrm {KF}^{{{\rm int}}}$
and
![]() $\mathrm {KF}^-$
is dispensable, and, in this sense, both theories can be given an instrumentalist interpretation as suggested by Reinhardt. Moreover, building on results by Halbach & Horsten [Reference Halbach and Horsten10], Halbach & Nicolai [Reference Halbach and Nicolai11], and Nicolai [Reference Nicolai14], we have shown how to provide independent axiomatizations of the significant part of
$\mathrm {KF}^-$
is dispensable, and, in this sense, both theories can be given an instrumentalist interpretation as suggested by Reinhardt. Moreover, building on results by Halbach & Horsten [Reference Halbach and Horsten10], Halbach & Nicolai [Reference Halbach and Nicolai11], and Nicolai [Reference Nicolai14], we have shown how to provide independent axiomatizations of the significant part of
![]() $\mathrm {KF}$
-like theories with restricted forms of induction in non-classical logic. This was precisely the content of Reinhardt’s challenge. Our results thus get us some way to completing Reinhardt’s program and, at least as far as the
$\mathrm {KF}$
-like theories with restricted forms of induction in non-classical logic. This was precisely the content of Reinhardt’s challenge. Our results thus get us some way to completing Reinhardt’s program and, at least as far as the
![]() $\mathrm {KF}$
-theories with restricted forms of induction are concerned, they fully “justify the use of nonsignificant sentences entirely within the framework of significant sentences” [Reference Reinhardt21, p. 225].
$\mathrm {KF}$
-theories with restricted forms of induction are concerned, they fully “justify the use of nonsignificant sentences entirely within the framework of significant sentences” [Reference Reinhardt21, p. 225].
However, to complete Reinhardt’s program and prove it successful will require answering Reinhardt’s challenge for
![]() $\mathrm {KF}$
-like theories with full induction. To this effect one needs to pair
$\mathrm {KF}$
-like theories with full induction. To this effect one needs to pair
![]() $\mathrm {KF}$
-like theories with suitable non-classical truth theories. In light of Nicolai’s [Reference Nicolai14] work, it seems very likely that these non-classical theories will be versions of
$\mathrm {KF}$
-like theories with suitable non-classical truth theories. In light of Nicolai’s [Reference Nicolai14] work, it seems very likely that these non-classical theories will be versions of
![]() $\mathrm {PKF}^+$
, although a proof of this conjecture is left for future research. Let us assume for now that
$\mathrm {PKF}^+$
, although a proof of this conjecture is left for future research. Let us assume for now that
![]() $\mathrm {PKF}^+$
-like theories indeed answer Reinhardt’s Challenge for
$\mathrm {PKF}^+$
-like theories indeed answer Reinhardt’s Challenge for
![]() $\mathrm {KF}$
theories with full induction. Should we conclude that we have justified the use of nonsignificant sentences entirely within the framework of significant sentences? Should we deem Reinhardt’s program successful? In contrast to the case of
$\mathrm {KF}$
theories with full induction. Should we conclude that we have justified the use of nonsignificant sentences entirely within the framework of significant sentences? Should we deem Reinhardt’s program successful? In contrast to the case of
![]() $\mathrm {KF}$
-like theories with restricted forms of induction, an answer to this question seems to be less straightforward, as one may query whether
$\mathrm {KF}$
-like theories with restricted forms of induction, an answer to this question seems to be less straightforward, as one may query whether
![]() $\mathrm {PKF}^+$
amounts to an independent axiomatization of the significant part of
$\mathrm {PKF}^+$
amounts to an independent axiomatization of the significant part of
![]() $\mathrm {KF}$
. The crucial question is whether the rule
$\mathrm {KF}$
. The crucial question is whether the rule
![]() $\mathrm {TI}^{<\varepsilon _0}$
is available from within the significant framework. Ultimately, an answer to this question will depend on the role the theory of truth is supposed to play within one’s theoretical framework. If, for instance, one takes the theory to play an important role in the foundations of mathematics and an important role in singling out the limits of predicativity Feferman [Reference Feferman6], then one should arguably refrain from thinking that
$\mathrm {TI}^{<\varepsilon _0}$
is available from within the significant framework. Ultimately, an answer to this question will depend on the role the theory of truth is supposed to play within one’s theoretical framework. If, for instance, one takes the theory to play an important role in the foundations of mathematics and an important role in singling out the limits of predicativity Feferman [Reference Feferman6], then one should arguably refrain from thinking that
![]() $\mathrm {TI}^{<\varepsilon _0}$
can be assumed without further justification from within the significant framework. But, to the contrary, if the theory of truth is to play no role in the foundations of mathematics and classical mathematical theorizing is freely available from within the significant framework, then it is hard to see why
$\mathrm {TI}^{<\varepsilon _0}$
can be assumed without further justification from within the significant framework. But, to the contrary, if the theory of truth is to play no role in the foundations of mathematics and classical mathematical theorizing is freely available from within the significant framework, then it is hard to see why
![]() $\mathrm {TI}^{<\varepsilon _0}$
should not be considered as fully justified from within the significant perspective.Footnote
31
In this case it would seem that Reinhardt’s program needs to be deemed successful once Theorem 4.8 has been extended to the theory pair
$\mathrm {TI}^{<\varepsilon _0}$
should not be considered as fully justified from within the significant perspective.Footnote
31
In this case it would seem that Reinhardt’s program needs to be deemed successful once Theorem 4.8 has been extended to the theory pair
![]() $\left \langle \mathrm {KF},\mathrm {PKF}^+\right \rangle $
. Of course, such a generalization of Theorem 4.8 is yet to be provided, but the understanding of Reinhardt’s program developed in this paper together with the results for
$\left \langle \mathrm {KF},\mathrm {PKF}^+\right \rangle $
. Of course, such a generalization of Theorem 4.8 is yet to be provided, but the understanding of Reinhardt’s program developed in this paper together with the results for
![]() $\mathrm {KF}$
-variants with restricted forms of induction suggests there is no principled obstacle in way of a successful completion of Reinhardt’s program. Thus, after all, it seems that Reinhardt was right in claiming that “the chances of success in this context
$\mathrm {KF}$
-variants with restricted forms of induction suggests there is no principled obstacle in way of a successful completion of Reinhardt’s program. Thus, after all, it seems that Reinhardt was right in claiming that “the chances of success in this context
![]() $(\cdots )$
are somewhat better than in Hilbert’s context” [Reference Reinhardt21, p. 225].
$(\cdots )$
are somewhat better than in Hilbert’s context” [Reference Reinhardt21, p. 225].
Acknowledgements
We thank two anonymous referees for very helpful comments that led to a significant improvement of the paper. In particular, we wish to thank one referee for catching a serious mistake in our paper. We also wish to thank Martin Fischer and Carlo Nicolai for their invaluable comments on the paper and discussions of the material. Johannes Stern’s research was supported by the ERC Starting Grant TRUST, Grant No. 803684. Luca Castaldo’s research was supported by the AHRC South, West and Wales Doctoral Training Partnership (SWW DTP), Grant No. AH/L503939/1-DTP1.