Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-20T05:31:25.864Z Has data issue: false hasContentIssue false
  • English
  • Français

LOGICS OF FORMAL INCONSISTENCY ENRICHED WITH REPLACEMENT: AN ALGEBRAIC AND MODAL ACCOUNT

Part of: Algebraic logic General logic

Published online by Cambridge University Press:  02 July 2021

WALTER CARNIELLI ,
MARCELO E. CONIGLIO  and
DAVID FUENMAYOR
WALTER CARNIELLI
Affiliation:
CENTRE FOR LOGIC, EPISTEMOLOGY, AND THE HISTORY OF SCIENCE (CLE) UNIVERSITY OF CAMPINAS (UNICAMP) R. SÉRGIO BUARQUE DE HOLANDA, 251, CAMPINAS-SP13083-859, BRAZILE-mail: [email protected]
MARCELO E. CONIGLIO
Affiliation:
INSTITUTE OF PHILOSOPHY AND THE HUMANITIES (IFCH) UNIVERSITY OF CAMPINAS (UNICAMP) R. CORA CORALINA, 100, CAMPINAS-SP13083-896, BRAZIL and CENTRE FOR LOGIC, EPISTEMOLOGY, AND THE HISTORY OF SCIENCE (CLE) UNIVERSITY OF CAMPINAS (UNICAMP) R. CORA CORALINA, 100, CAMPINAS-SP13083-896, BRAZILE-mail: [email protected]
DAVID FUENMAYOR
Affiliation:
INDIVIDUAL AND COLLECTIVE REASONING GROUP (ICR) DEPARTMENT OF COMPUTER SCIENCE UNIVERSITY OF LUXEMBOURG 6, AVENUE DE LA FONTE, ESCH-SUR-ALZETTE L-4364, LUXEMBOURG and INSTITUTE OF COMPUTER SCIENCE FREIE UNIVERSITÄT BERLIN ARNIMALLEE 7, 14195BERLIN, GERMANYE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is customary to expect from a logical system that it can be algebraizable, in the sense that an algebraic companion of the deductive machinery can always be found. Since the inception of da Costa’s paraconsistent calculi, algebraic equivalents for such systems have been sought. It is known, however, that these systems are not self-extensional (i.e., they do not satisfy the replacement property). More than this, they are not algebraizable in the sense of Blok–Pigozzi. The same negative results hold for several systems of the hierarchy of paraconsistent logics known as Logics of Formal Inconsistency (LFIs). Because of this, several systems belonging to this class of logics are only characterizable by semantics of a non-deterministic nature. This paper offers a solution for two open problems in the domain of paraconsistency, in particular connected to algebraization of LFIs, by extending with rules several LFIs weaker than 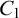$C_1$ , thus obtaining the replacement property (that is, such LFIs turn out to be self-extensional). Moreover, these logics become algebraizable in the standard Lindenbaum–Tarski’s sense by a suitable variety of Boolean algebras extended with additional operations. The weakest LFI satisfying replacement presented here is called RmbC, which is obtained from the basic LFI called mbC. Some axiomatic extensions of RmbC are also studied. In addition, a neighborhood semantics is defined for such systems. It is shown that RmbC can be defined within the minimal bimodal non-normal logic $\mathbf {E} {\oplus } \mathbf {E}$ defined by the fusion of the non-normal modal logic E with itself. Finally, the framework is extended to first-order languages. RQmbC, the quantified extension of RmbC, is shown to be sound and complete w.r.t. the proposed algebraic semantics.

Keywords

logics of formal inconsistencyparaconsistent logicsreplacement propertyalgebraizable logicsnon-normal modal logicneighborhood semanticsfirst-order paraconsistent logicsBoolean algebras with additional operators

MSC classification

Primary: 03B45: Modal logic (including the logic of norms)
Secondary: 03G27: Abstract algebraic logic 03B62: Combined logics
Type
Research Article
Information
The Review of Symbolic Logic , Volume 15 , Issue 3 , September 2022 , pp. 771 - 806
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arruda, A. I., & da Costa, N. C. A. (1970). Sur le schéma de la séparation. Nagoya Mathematical Journal, 38, 71–84.CrossRefGoogle Scholar
Avron, A. (2005). Non-deterministic matrices and modular semantics of rules. In Béziau, J.-Y., editor. Logica Universalis. Basel: Birkhäuser, pp. 149–167.CrossRefGoogle Scholar
Avron, A.. (2017). Self-extensional three-valued paraconsistent logics. Logica Universalis, 11, 297–315.CrossRefGoogle Scholar
Avron, A., & Béziau, J. Y. (2017). Self-extensional three-valued paraconsistent logics have no implication. Logic Journal of the IGPL, 25(2), 183–194.Google Scholar
Avron, A., & Zamansky, A. (2016). A paraconsistent view on B and S5. In Beklemishev, L., Demri, S., and Máté, A., editors. Advances in Modal Logic, Vol. 11. London: College Publications, pp. 21–37.Google Scholar
Bell, J. L. (2005). Set Theory: Boolean-Valued Models and Independence Proofs (third edition). Oxford Logic Guides, Vol. 47. Oxford: Oxford University Press.CrossRefGoogle Scholar
Benzmüller, C. (2019). Universal (meta-)logical reasoning: recent successes. Science of Computer Programming, 172, 48–62.CrossRefGoogle Scholar
Béziau, J.-Y. (1998). Idempotent full paraconsistent negations are not algebraizable. Notre Dame Journal of Formal Logic, 39(1), 135–139.CrossRefGoogle Scholar
Béziau, J.-Y.. (2002). S5 is a paraconsistent logic and so is first-order classical logic. Logical Studies, 9, 301–309.Google Scholar
Béziau, J.-Y.. (2005). Paraconsistent logic from a modal viewpoint. Journal of Applied Logic, 3, 7–14.CrossRefGoogle Scholar
Blanchette, J. C., & Nipkow, T. (2010). Nitpick: A counterexample generator for higher-order logic based on a relational model finder. In Kaufmann, M. and Paulson, L. C., editors. Interactive Theorem Proving (ITP 2010). Lecture Notes in Computer Science, Vol. 6172. New York:Springer, pp. 131–146.CrossRefGoogle Scholar
Blok, W. J., & Pigozzi, D. (1989). Algebraizable Logics. Memoirs of the American Mathematical Society, Vol. 77. Providence, RI: American Mathematical Society.CrossRefGoogle Scholar
Bou, F., Esteva, F., Font, J. M., Gil, A., Godo, L. A. T., & Verdú, V. (2009). Logics preserving degrees of truth from varieties of residuated lattices. Journal of Logic and Computation, 19(6), 1031–1069.CrossRefGoogle Scholar
Bueno-Soler, J., & Carnielli, W. (2017). Experimenting with consistency. In Markin, V. and Zaitsev, D., editors. The Logical Legacy of Nikolai Vasiliev and Modern Logic. Synthese Library (Studies in Epistemology, Logic, Methodology, and Philosophy of Science), Vol. 387. Cham, Switzerland:Springer, pp. 199–221.CrossRefGoogle Scholar
Carnielli, W. A., & Coniglio, M. E. (2016a). Paraconsistent Logic: Consistency, Contradiction and Negation. Logic, Epistemology, and the Unity of Science, Vol. 40. Cham, Switzerland: Springer.Google Scholar
Carnielli, W. A., & Coniglio, M. E.. (2016b). Paraconsistent set theory by predicating on consistency. Journal of Logic and Computation, 26(1), 97–116.CrossRefGoogle Scholar
Carnielli, W. A., & Coniglio, M. E.. (2020). Combining logics. InZalta, E. N., editor. The Stanford Encyclopedia of Philosophy (Fall 2020 edition). Available from: http://plato.stanford.edu/archives/spr2014/entries/logic-combining.Google Scholar
Carnielli, W. A., & Coniglio, M. E.. (2021). Twist-valued models for three-valued paraconsistent set theory. Logic and Logical Philosophy. 30(2), 187–226.Google Scholar
Carnielli, W. A., Coniglio, M. E., Gabbay, D. M., Gouveia, P., & Sernadas, C. (2008). Analysis and Synthesis of Logics: How to Cut and Paste Reasoning Systems. Applied Logic Series, Vol. 35. New York: Springer.Google Scholar
Carnielli, W. A., Coniglio, M. E., & Marcos, J. (2007). Logics of formal inconsistency. In Gabbay, D. M. and Guenthner, F., editors, Handbook of Philosophical Logic (second edition), Vol. 14. Dordrecht: Springer, pp. 1–93.Google Scholar
Carnielli, W. A., Coniglio, M. E., Podiacki, R., & Rodrigues, T. (2014). On the way to a wider model theory: Completeness theorems for first-order logics of formal inconsistency. The Review of Symbolic Logic, 7(3), 548–578.CrossRefGoogle Scholar
Carnielli, W. A., & de Alcantara, L. P. (1984). Paraconsistent algebras. Studia Logica, 43(1/2), 79–88.CrossRefGoogle Scholar
Carnielli, W. A., & Lima-Marques, M. (1999). Society semantics and multiple-valued logics. In Carnielli, W. A. and D’Ottaviano, I. M., editors, Advances in Contemporary Logic and Computer Science. Proceedings of the XI Brazilian Conference on Mathematical Logics, May 1996, Salvador, Bahia, Brazil. Contemporary Mathematics, Vol. 235. Providence, RI: American Mathematical Society, pp. 33–52.CrossRefGoogle Scholar
Carnielli, W. A., & Marcos, J. (2002). A taxonomy of C-systems. In Carnielli, W. A., Coniglio, M. E., and D’Ottaviano, I. M. L., editors. Paraconsistency: The Logical Way to the Inconsistent. Proceedings of the 2 nd World Congress on Paraconsistency (WCP 2000). Lecture Notes in Pure and Applied Mathematics, Vol. 228. New York: Marcel Dekker, pp. 1–94.CrossRefGoogle Scholar
Chellas, B. (1980). Modal Logic: An Introduction. New York: Cambridge University Press.CrossRefGoogle Scholar
Coniglio, M., Figallo-Orellano, A., & Golzio, A. C. (2020). First-order swap structures semantics for some logics of formal inconsistency. Journal of Logic and Computation, 30(6), 1257–1290.CrossRefGoogle Scholar
Coniglio, M., & Prieto-Sanabria, L. (2017). Modal logic S4 as a paraconsistent logic with a topological semantics. In Gouveia, P., Carlos, C., and Donisio, F., editors. Logic and Computation: Essays in Honour of Amilcar Sernadas. Tributes, Vol. 33. London: College Publications, pp. 171–196.Google Scholar
Coniglio, M. E., Esteva, F., & Godo, L. (2014). Logics of formal inconsistency arising from systems of fuzzy logic. Logic Journal of the IGPL, 22(6), 880–904.CrossRefGoogle Scholar
Coniglio, M. E., & Toledo, G. V. (2021). A simple decision procedure for da Costa’s ${C}_n$ logics by Restricted Nmatrix semantics. Preprint, arXiv:2011.10151.Google Scholar
Curry, H. B. (1963). Foundations of Mathematical Logic. New York: McGrawHill.Google Scholar
da Costa, N. C. A. (1963). Sistemas Formais Inconsistentes (Inconsistent Formal Systems, in Portuguese). Habilitation Thesis, Universidade Federal do Paraná, Curitiba, Brazil. Republished by Editora UFPR, Curitiba, Brazil, 1993.Google Scholar
da Costa, N. C. A., & Guillaume, M. (1964). Sur les calculs Cn. Anais da Academia Brasileira de Ciências, 36, 379–382.Google Scholar
de Araújo, A. L., Alves, E. H., & Guerzoni, J. A. D. (1987). Some relations between modal and paraconsistent logic. The Journal of Non-Classical Logic, 4(2), 33–44. Available from: http://www.cle.unicamp.br/jancl.Google Scholar
Došen, K. (1984). Negative modal operators in intuitionistic logic. Publications de l’Institut Mathématique. Nouvelle Série, 35(49), 3–14.Google Scholar
Došen, K.. (1986). Negation as a modal operator. Reports on Mathematical Logic, 20, 15–27.Google Scholar
Dunn, J. M. (1993). Star and perp: Two treatments of negation. Philosophical Perspectives, 7, 331–357.CrossRefGoogle Scholar
Dunn, J. M., & Hardegree, G. M. (2001). Algebraic Methods in Philosophical Logic. Oxford Logic Guides, Vol. 41. Oxford: Oxford University Press.Google Scholar
Dunn, J. M., & Zhou, C. (2005). Negation in the context of gaggle theory. Studia Logica, 80(2–3), 235–264.CrossRefGoogle Scholar
Ertola, R., Esteva, F., Flaminio, T., Godo, L., & Noguera, C. (2015). Exploring paraconsistency in degree-preserving fuzzy logics. Soft Computing, 19(3), 531–546.CrossRefGoogle Scholar
Fuenmayor, D. (2020). Topological semantics for paraconsistent and paracomplete logics. Archive of Formal Proofs. Available from: https://isa-afp.org/entries/Topological_Semantics.html.Google Scholar
Gabbay, D. M. (1975). A normal logic that is complete for neighborhood frames but not for Kripke frames. Theoria, 41(3), 148–153.CrossRefGoogle Scholar
Givant, S., & Halmos, P. (2009). Introduction to Boolean Algebras. New York: Springer.Google Scholar
Henkin, L. (1949). Fragments of the propositional calculus. The Journal of Symbolic Logic, 14(1), 42–48.CrossRefGoogle Scholar
Jónsson, B. (1993). A survey of Boolean algebras with operators. In Rosenberg, I. and Sabidussi, G., editors. Algebras and Orders. NATO ASI Series (Series C: Mathematical and Physical Sciences), Vol. 389. Dordrecht: Springer, pp. 239–286.CrossRefGoogle Scholar
Lewin, R. A., Mikenberg, I. F., & Schwarze, M. G. (1991). C 1 is not algebraizable. Notre Dame Journal of Formal Logic, 32(4), 609–611.CrossRefGoogle Scholar
Lewis, D. K. (1973). Counterfactuals. Cambridge, MA: Harvard University Press.Google Scholar
Łukasiewicz, J. (1948–1950). The shortest axiom of the implicational calculus of propositions. Proceedings of the Royal Irish Academy Section A: Mathematical and Physical Sciences, 52, 25–33.Google Scholar
MacNeille, H. (1937). Partially ordered sets. Transactions of the American Mathematical Society, 42, 416–460.CrossRefGoogle Scholar
Marcos, J. (2005a). Modality and paraconsistency. In Bilkova, M. and Behounek, L., editors. The Logica Yearbook 2004, Proceedings of the XVIII International Symposium promoted by the Institute of Philosophy of the Academy of Sciences of the Czech Republic. Prague: Filosofia, pp. 213–222.Google Scholar
Marcos, J.. (2005b). Nearly every normal modal logic is paranormal. Logique et Analyse, 48(189–192), 279–300.Google Scholar
Montague, R. (1970). Universal grammar. Theoria, 36, 373–398.CrossRefGoogle Scholar
Mortensen, C. (1980). Every quotient algebra for C 1 is trivial. Notre Dame Journal of Formal Logic, 21(4), 694–700.CrossRefGoogle Scholar
Mortensen, C. (1989). Paraconsistency and C 1 . In Priest, G., Routley, R., and Norman, J., editors. Paraconsistent Logic: Essays on the Inconsistent. Munich: Philosophia, pp. 289–305.Google Scholar
Nipkow, T., Paulson, L. C., & Wenzel, M. (2002). Isabelle/HOL: A Proof Assistant for Higher-Order Logic. Lecture Notes in Computer Science, Vol. 2283. Berlin: Springer.CrossRefGoogle Scholar
Pacuit, E. (2017). Neighborhood Semantics for Modal Logic. Cham, Switzerland: Springer.CrossRefGoogle Scholar
Scott, D. (1970). Advice in modal logic. In Lambert, K., editor. Philosophical Problems in Logic: Some Recent Developments. Synthese Library (Monographs on Epistemology, Logic, Methodology, Philosophy of Science, Sociology of Science and of Knowledge, and on the Mathematical Methods of Social and Behavioral Sciences), Vol. 29. Dordrecht: D. Reidel, pp. 143–173.CrossRefGoogle Scholar
Segerberg, K. (1982). Classical Propositional Operators: An Exercise in the Foundations of Logic. Oxford Logic Guides, Vol. 5. Oxford: Clarendon Press.Google Scholar
Seoane, J., & de Alcantara, L. P. (1991). On da Costa algebras. The Journal of Non-Classical Logic, 8(2), 41–66. Available from: http://www.cle.unicamp.br/jancl.Google Scholar
Stone, M. H. (1936). The theory of representations of Boolean algebras. Transactions of the American Mathematical Society, 40, 37–111.Google Scholar
Sylvan, R. (1990). Variations on da costa C systems and dual-intuitionistic logics I. Analyses of Cω and CCω . Studia Logica, 49(1), 47–65.CrossRefGoogle Scholar
Tarski, A. (1937). Über additive und multiplikative Mengenkörper und Mengenfunktionen. Sprawozdania z Posiedzeń Towarzystwa Naukowego Warszawskiego Wydział III Nauk Matematyczno-fizycznych (=Comptes Rendus des Séances de la Société des Sciences et des Lettres de Varsovie, Classe III), 30, 151–181.Google Scholar
Urbas, I. (1987). On Brazilian Paraconsistent Logics. Ph.D. Thesis, Australian National University, Canberra, Australia.Google Scholar
Urbas, I.. (1989). Paraconsistency and the C-Systems of da Costa. Notre Dame Journal of Formal Logic, 30(4), 583–597.CrossRefGoogle Scholar
Vakarelov, D. (1989). Consistency, completeness and negation. In Priest, G., Routley, R., and Norman, J., editors. Paraconsistent Logic: Essays on the Inconsistent. Munich: Philosophia, pp. 328–363.Google Scholar
Zanardo, A., Sernadas, A., & Sernadas, C. (2001). Fibring: Completeness preservation. The Journal of Symbolic Logic, 66(1), 414–439.CrossRefGoogle Scholar