It’s well known that it’s possible to extract, from Frege’s Grudgesetze, an interpretation of second-order Peano Arithmetic in the theory 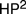$H{P^2}$, whose sole axiom is Hume’s principle. What’s less well known is that, in Die Grundlagen Der Arithmetic §82–83 Boolos (2011), George Boolos provided a converse interpretation of 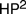$H{P^2}$ in 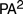$P{A^2}$. Boolos’ interpretation can be used to show that the Frege’s construction allows for any model of 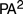$P{A^2}$ to be recovered from some model of 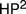$H{P^2}$. So the space of possible arithmetical universes is precisely characterized by Hume’s principle.

In this paper, I show that a large class of second-order theories admit characterization by an abstraction principle in this sense. The proof makes use of structural abstraction principles, a class of abstraction principles of considerable intrinsic interest, and categories of interpretations in the sense of Visser (2003).