No CrossRef data available.
Article contents
FINITARY UPPER LOGICISM
Published online by Cambridge University Press: 31 May 2024
Abstract
This paper proposes and partially defends a novel philosophy of arithmetic—finitary upper logicism. According to it, the natural numbers are finite cardinalities—conceived of as properties of properties—and arithmetic is nothing but higher-order modal logic. Finitary upper logicism is furthermore essentially committed to the logicality of finitary plenitude, the principle according to which every finite cardinality could have been instantiated. Among other things, it is proved in the paper that second-order Peano arithmetic is interpretable, on the basis of the finite cardinalities’ conception of the natural numbers, in a weak modal type theory consisting of the modal logic 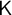 $\mathsf {K}$, negative free quantified logic, a contingentist-friendly comprehension principle, and finitary plenitude. By replacing finitary plenitude for the axiom of infinity this result constitutes a significant improvement on Russell and Whitehead’s interpretation of second-order Peano arithmetic, itself based on the finite cardinalities’ conception of the natural numbers.
$\mathsf {K}$, negative free quantified logic, a contingentist-friendly comprehension principle, and finitary plenitude. By replacing finitary plenitude for the axiom of infinity this result constitutes a significant improvement on Russell and Whitehead’s interpretation of second-order Peano arithmetic, itself based on the finite cardinalities’ conception of the natural numbers.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



