Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T22:50:07.530Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FINE STRUCTURE OF THE INTUITIONISTIC BOREL HIERARCHY

Published online by Cambridge University Press:  01 March 2009

WIM VELDMAN
WIM VELDMAN*
Affiliation:
Institute for Mathematics, Astrophysics and Particle Physics, Faculty of Science, Radboud University Nijmegen
*
*INSTITUTE FOR MATHEMATICS, ASTROPHYSICS AND PARTICLE PHYSICS, FACULTY OF SCIENCE, RADBOUD UNIVERSITY NIJMEGEN, POSTBUS 9044, 6500 KD NIJMEGEN, THE NETHERLANDS, E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In intuitionistic analysis, a subset of a Polish space like ℝ or 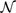is called positively Borel if and only if it is an open subset of the space or a closed subset of the space or the result of forming either the countable union or the countable intersection of an infinite sequence of (earlier constructed) positively Borel subsets of the space. The operation of taking the complement is absent from this inductive definition, and, in fact, the complement of a positively Borel set is not always positively Borel itself (see Veldman, 2008a). The main result of Veldman (2008a) is that, assuming Brouwer's Continuity Principle and an Axiom of Countable Choice, one may prove that the hierarchy formed by the positively Borel sets is genuinely growing: every level of the hierarchy contains sets that do not occur at any lower level. The purpose of the present paper is a different one: we want to explore the truly remarkable fine structure of the hierarchy. Brouwer's Continuity Principle again is our main tool. A second axiom proposed by Brouwer, his Thesis on Bars is also used, but only incidentally.

Type
Research Article
Information
The Review of Symbolic Logic , Volume 2 , Issue 1 , March 2009 , pp. 30 - 101
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Bishop, E., & Bridges, D. (1985). Constructive Analysis. Berlin, Germany: Springer-Verlag.CrossRefGoogle Scholar
Brouwer, L. E. J. (1918). Begründung der Mengenlehre unabhängig vom logischen Satz vom ausgeschlossenen Dritten. Erster Teil: Allgemeine Mengenlehre. Koninklijke Nederlandsche Akademie van Wetenschappen, Verhandelingen, 1e sectie 12, no.5, 43 pp., 1918, also Brouwer (1975), pp. 150–190, with footnotes, pp. 573–585.Google Scholar
Brouwer, L. E. J. (1927). Über Definitionsbereiche von Funktionen. Mathematische Annalen, 97, 60–75. Also in Brouwer (1975), pp. 390–405, see also van Heijenoort (1967), pp. 446–463.CrossRefGoogle Scholar
Brouwer, L. E. J. (1954). Points and spaces. Canadian Journal of Mathematics, 6, 1–17. Also in (Brouwer(1975)), pp. 522–538.CrossRefGoogle Scholar
Brouwer, L. E. J. (1975). Heyting, A., editor. Collected Works, Vol. I: Philosophy and Foundations of Mathematics. Amsterdam, The Netherlands: North-Holland.Google Scholar
Kechris, A. S. (1996). Classical Descriptive Set Theory. Berlin, Germany: Springer-Verlag.Google Scholar
Kleene, S. C., & Vesley, R. E. (1965). The Foundations of Intuitionistic Mathematics, Especially in Relation to Recursive Functions. Amsterdam, The Netherlands: North-Holland.Google Scholar
Lusin, N. (1930). Leçons sur les ensembles analytiques et leurs applications (second edition). Paris, France. New York: Chelsea Publishing Company(1972).Google Scholar
Moschovakis, Y. N. (1980). Descriptive Set Theory. Amsterdam, The Netherlands: North-Holland.Google Scholar
van Dantzig, D. (1947). On the principles of intuitionistic and affirmative mathematics. Proceedings Koninklijke Nederlandse Akademie van Wetenschappen, 50, 918–929 and 1092–1103; Indagationes Mathematicae, 9, 429–440 and 506–517.Google Scholar
van Heijenoort, J. (1967). From Frege to Gödel, A Source Book in Mathematical Logic, 1879-1931. Cambridge, MA: Harvard University Press.Google Scholar
Veldman, W. (1981). Investigations in Intuitionistic Hierarchy Theory. PhD Thesis, Katholieke Universiteit Nijmegen.Google Scholar
Veldman, W. (1990). A survey of intuitionistic descriptive set theory. In Petkov, P. P., editor. Mathematical Logic, Proceedings of the Heyting Conference 1988. New York: Plenum Press, pp. 155–174.Google Scholar
Veldman, W. (1995). Some intuitionistic variations on the notion of a finite set of natural numbers. In de Swart, H. C. M., and Bergmans, L. J. M., editors. Perspectives on Negation, Essays in Honour of Johan J. de Iongh on the Occasion of his 80th Birthday. Tilburg, The Netherlands: Tilburg University Press, pp. 177–202.Google Scholar
Veldman, W. (1999). On sets enclosed between a set and its double complement. In Cantini e.a., A., editor. Logic and Foundations of Mathematics, Proceedings Xth International Congress on Logic, Methodology and Philosophy of Science, Florence 1995, Vol. III. Dordrecht, The Netherlands: Kluwer Academic Publishers, pp. 143–154.Google Scholar
Veldman, W. (2001). Understanding and using Brouwer’s continuity principle. In Berger, U., Osswald, H., and Schuster, P., editors. Reuniting the Antipodes, Constructive and Nonstandard Views of the Continuum, Proceedings of a Symposium held in San Servolo/Venice, 1999. Dordrecht, The Netherlands: Kluwer Academic Publishers, pp. 285–302.Google Scholar
Veldman, W. (2003a). The Cantor-Bendixson-hierarchy revisited by Brouwer. In Vahidi-Asl, M. Q. and Zokaei, M., editors. Proceedings of the First Seminar on the Philosophy of Mathematics in Iran, October 17, 2001. Teheran, Iran: Faculty of Mathematical Sciences, Shahid Beheshti University, pp. 79–103.Google Scholar
Veldman, W. (2003b). On the persistent difficulty of disjunction. In Rojszczak, A., Cachro, J., and Kurczewski, G., editors. Philosophical Dimensions of Logic and Science, Selected Contributed Papers From the 11th International Congress on Logic, Methodology and Philosophy of Science, Kraków, 1999. Dordrecht, The Netherlands: Kluwer Academic Publishers, pp. 77–90.Google Scholar
Veldman, W. (2004). An intuitionistic proof of Kruskal's theorem. Archive for Mathematical Logic, 43, 215–264.CrossRefGoogle Scholar
Veldman, W. (2005a). Brouwer's Fan Theorem as an axiom and as a contrast to Kleene's Alternative. Report No. 0509, Department of Mathematics, Radboud University Nijmegen.Google Scholar
Veldman, W. (2005b). Perhaps the Intermediate Value Theorem. In Calude, C. S., and Ishihara, H., editors. Constructivity, Computability and Logic. A Collection of Papers in Honour of the 60th Birthday of Douglas Bridges. Journal of Universal Computer Science, 11, 2142–2158.Google Scholar
Veldman, W. (2005c). Two simple sets that are not positively Borel. Annals of Pure and Applied Logic, 135, 151–209.CrossRefGoogle Scholar
Veldman, W. (2006a). The Borel Hierarchy and the Projective Hierarchy from Brouwer's intuitionistic perspective. Report No. 0604. Department of Mathematics, Radboud University Nijmegen.Google Scholar
Veldman, W. (2006b). Brouwer’s real Thesis on Bars. In Heinzmann, G., and Ronzitti, G., editors. Constructivism: Mathematics, Logic, Philosophy and Linguistics, Philosophia Scientiae, Cahier spécial, 6, pp. 21–42.Google Scholar
Veldman, W. (2008a). The Borel Hierarchy Theorem from Brouwer's intuitionistic perspective. The Journal of Symbolic Logic, 73, 1–64.CrossRefGoogle Scholar
Veldman, W. (2008b). Some applications of Brouwer's Thesis on Bars. In van Atten, M., Boldini, P., Bourdeau, M., and Heinzmann, G., editors. One Hundred Years of Intuitionism, the Cerisy Conference. Basel, Switzerland: Birkhäuser, pp. 326–340.CrossRefGoogle Scholar
Waaldijk, F. A. (1996). Modern intuitionistic topology. PhD Thesis, Katholieke Universiteit Nijmegen.Google Scholar