Article contents
DYNAMIC CONSEQUENCE AND PUBLIC ANNOUNCEMENT
Published online by Cambridge University Press: 14 October 2013
Abstract
In van Benthem (2008), van Benthem proposes a dynamic consequence relation defined as 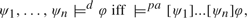 ${\psi _1}, \ldots ,{\psi _n}{ \models ^d}\phi \,{\rm{iff}}{ \models ^{pa}}[{\psi _1}] \ldots [{\psi _n}]\phi ,$ where the latter denotes consequence in public announcement logic, a dynamic epistemic logic. In this paper we investigate the structural properties of a conditional dynamic consequence relation
${\psi _1}, \ldots ,{\psi _n}{ \models ^d}\phi \,{\rm{iff}}{ \models ^{pa}}[{\psi _1}] \ldots [{\psi _n}]\phi ,$ where the latter denotes consequence in public announcement logic, a dynamic epistemic logic. In this paper we investigate the structural properties of a conditional dynamic consequence relation  $\models _{\rm{\Gamma }}^d$ extending van Benthem’s proposal. It takes into account a set of background conditions Γ, inspired by Makinson (2003) wherein Makinson calls this reasoning ‘modulo’ a set Γ. In the presence of common knowledge, conditional dynamic consequence is definable from (unconditional) dynamic consequence. An open question is whether dynamic consequence is compact. We further investigate a dynamic consequence relation for soft instead of hard announcements. Surprisingly, it shares many properties with (hard) dynamic consequence. Dynamic consequence relations provide a novel perspective on reasoning about protocols in multi-agent systems.
$\models _{\rm{\Gamma }}^d$ extending van Benthem’s proposal. It takes into account a set of background conditions Γ, inspired by Makinson (2003) wherein Makinson calls this reasoning ‘modulo’ a set Γ. In the presence of common knowledge, conditional dynamic consequence is definable from (unconditional) dynamic consequence. An open question is whether dynamic consequence is compact. We further investigate a dynamic consequence relation for soft instead of hard announcements. Surprisingly, it shares many properties with (hard) dynamic consequence. Dynamic consequence relations provide a novel perspective on reasoning about protocols in multi-agent systems.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2013
References
BIBLIOGRAPHY
- 2
- Cited by


