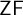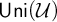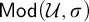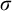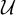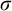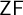1 Introduction
![]() $\mathsf {ZF}$
set theory serves as a foundation for mathematics, but has also turned out to be interesting in itself as a field of mathematical study. Much of the interest lies in that it raises questions that are not only undecidable, but also lacking clear-cut intuitive answers and demanding deep mathematical developments. The continuum hypothesis is a primary historical example: It seems implausible to reach a consensus on affirming or denying it, and it motivated two techniques central to set theory: the inner model and forcing constructions. It is natural to view these techniques as enabling constructions of set-theoretic universes from other set-theoretic universes, thus taking a multiverse view of the subject matter of set theory, rather than adopting the universe view that there is a single absolute universe of sets. In the words of Hamkins, an advocate of the multiverse view [Reference Hamkins12, p. 418]:
$\mathsf {ZF}$
set theory serves as a foundation for mathematics, but has also turned out to be interesting in itself as a field of mathematical study. Much of the interest lies in that it raises questions that are not only undecidable, but also lacking clear-cut intuitive answers and demanding deep mathematical developments. The continuum hypothesis is a primary historical example: It seems implausible to reach a consensus on affirming or denying it, and it motivated two techniques central to set theory: the inner model and forcing constructions. It is natural to view these techniques as enabling constructions of set-theoretic universes from other set-theoretic universes, thus taking a multiverse view of the subject matter of set theory, rather than adopting the universe view that there is a single absolute universe of sets. In the words of Hamkins, an advocate of the multiverse view [Reference Hamkins12, p. 418]:
A large part of set theory over the past half-century has been about constructing as many different models of set theory as possible /…/ Would you like to live in a universe where CH holds, but
![]() $\Diamond $
fails? Or where
$\Diamond $
fails? Or where
![]() $2^{\aleph _n} = \aleph _{n+2}$
for every natural number n? Would you like to have rigid Suslin trees? Would you like every Aronszajn tree to be special? Do you want a weakly compact cardinal
$2^{\aleph _n} = \aleph _{n+2}$
for every natural number n? Would you like to have rigid Suslin trees? Would you like every Aronszajn tree to be special? Do you want a weakly compact cardinal
![]() $\kappa $
for which
$\kappa $
for which
![]() $\Diamond _\kappa (\mathrm {REG})$
fails? Set theorists build models to order.
$\Diamond _\kappa (\mathrm {REG})$
fails? Set theorists build models to order.
Hamkins follows this perspective on set-theoretic practice with his argument for adopting the multiverse view:
This abundance of set-theoretic possibilities poses a serious difficulty for the universe view, for if one holds that there is a single absolute background concept of set, then one must explain or explain away as imaginary all of the alternative universes that set theorists seem to have constructed. This seems a difficult task, for we have a robust experience in those worlds, and they appear fully set theoretic to us. The multiverse view, in contrast, explains this experience by embracing them as real, filling out the vision hinted at in our mathematical experience, that there is an abundance of set-theoretic worlds into which our mathematical tools have allowed us to glimpse.
Methodologically, it makes sense to represent the universes of sets as models of a theory of sets, as that makes them accessible to the well-developed techniques of model theory. This raises two questions:
-
1. Which set theory?
-
2. Which models of that set theory?
In answer to the first question the authors have decided on limiting scope to
![]() $\mathsf {ZF}$
. This is the most utilized set theory, established in the mathematical community as a robust foundation of mathematics. All of the results of this paper go through for extensions of
$\mathsf {ZF}$
. This is the most utilized set theory, established in the mathematical community as a robust foundation of mathematics. All of the results of this paper go through for extensions of
![]() $\mathsf {ZF}$
(axiom of choice, large cardinals,
$\mathsf {ZF}$
(axiom of choice, large cardinals,
![]() $\dots $
). Although one development of this paper uses full
$\dots $
). Although one development of this paper uses full
![]() $\mathsf {ZF}$
,Footnote
1
the authors conjecture that for most of the results much weaker fragments suffice.
$\mathsf {ZF}$
,Footnote
1
the authors conjecture that for most of the results much weaker fragments suffice.
On the second question this paper takes a liberal approach. In particular, scope is not limited to well-founded models. The framework is intended to be applicable to a wide range of multiverse conceptions, for example the conceptions that every universe is of the form
![]() $V_\alpha $
, that every universe is well-founded, that every universe is countable and recursively saturated (and therefore ill-founded), or that every model is a universe.
$V_\alpha $
, that every universe is well-founded, that every universe is countable and recursively saturated (and therefore ill-founded), or that every model is a universe.
Why consider ill-founded universes? There is a sense in which a model
![]() $\mathcal {M}$
of set theory can be situated as an element in two different models
$\mathcal {M}$
of set theory can be situated as an element in two different models
![]() $\mathcal {N}_0$
and
$\mathcal {N}_0$
and
![]() $\mathcal {N}_1$
of set theory, such that
$\mathcal {N}_1$
of set theory, such that
![]() $\mathcal {N}_0$
satisfies that
$\mathcal {N}_0$
satisfies that
![]() $\mathcal {M}$
is well-founded while
$\mathcal {M}$
is well-founded while
![]() $\mathcal {N}_1$
satisfies that
$\mathcal {N}_1$
satisfies that
![]() $\mathcal {M}$
is ill-founded.Footnote
2
Thus, we may think of the property of well-foundedness as depending on the set-theoretic background. In Hamkins’s multiverse conception this is a key feature [Reference Hamkins12, pp. 438–439]:
$\mathcal {M}$
is ill-founded.Footnote
2
Thus, we may think of the property of well-foundedness as depending on the set-theoretic background. In Hamkins’s multiverse conception this is a key feature [Reference Hamkins12, pp. 438–439]:
The concept of well-foundedness [
![]() $\dots $
] depends on the set-theoretic background, for different models of set theory can disagree on whether a structure is well-founded. [
$\dots $
] depends on the set-theoretic background, for different models of set theory can disagree on whether a structure is well-founded. [
![]() $\dots $
] Indeed, every set-theoretic argument can take place in a model, which from the inside appears to be totally fine, but actually, the model is seen to be ill-founded from the external perspective of another, better model. Under the universe view, this problem terminates in the absolute set-theoretic background universe, which provides an accompanying absolute standard of well-foundedness. But the multiverse view allows for many different set-theoretic backgrounds, with varying concepts of the well-founded, and there seems to be no reason to support an absolute notion of well-foundedness.
$\dots $
] Indeed, every set-theoretic argument can take place in a model, which from the inside appears to be totally fine, but actually, the model is seen to be ill-founded from the external perspective of another, better model. Under the universe view, this problem terminates in the absolute set-theoretic background universe, which provides an accompanying absolute standard of well-foundedness. But the multiverse view allows for many different set-theoretic backgrounds, with varying concepts of the well-founded, and there seems to be no reason to support an absolute notion of well-foundedness.
To approach the set-theoretic multiverse mathematically, we need a foundational theory to situate the universes in. Just as the foundational background theory of
![]() $\mathsf {ZF}$
is useful for studying groups and topological spaces, it is useful for studying set-theoretic universes. So we find ourselves in a situation of studying models of
$\mathsf {ZF}$
is useful for studying groups and topological spaces, it is useful for studying set-theoretic universes. So we find ourselves in a situation of studying models of
![]() $\mathsf {ZF}$
from the background theory
$\mathsf {ZF}$
from the background theory
![]() $\mathsf {ZF}$
. The multiverse theorist may extend the background theory of
$\mathsf {ZF}$
. The multiverse theorist may extend the background theory of
![]() $\mathsf {ZF}$
to a multiverse theory (in an expanded language), with axioms specifying properties of the multiverse. In such a background multiverse theory, it is natural to consider the universes as themselves being models of multiverse theories, having their own internal universes, and so on. This raises an important question:
$\mathsf {ZF}$
to a multiverse theory (in an expanded language), with axioms specifying properties of the multiverse. In such a background multiverse theory, it is natural to consider the universes as themselves being models of multiverse theories, having their own internal universes, and so on. This raises an important question:
Main Question. What is the relationship between the external universe of the background multiverse theory, and the universes internal to the background theory? Similarly, what is the relationship between each universe and the universes within that universe?
We shall investigate several responses to the Main Question. Most fundamentally, the authors propose that the background multiverse theory obeys the following principle:
Copernican Principle. The background theory of the multiverse should not have a privileged position compared to the multiverse theories of the internal universes; specifically, if the background multiverse theory proves a statement, it should also prove that holds in all universes.
We have an analogy with the heliocentric model of the solar system: Earth corresponds to the universe of the background multiverse theory, as the basis for our point of view. The geocentric model gives earth a privileged central position as an absolute reference point, while the heliocentric model puts earth on a par with all of the planets. So the heliocentric model differs from the geocentric model in that it obeys the principle that for any appropriately fundamental assumption we make about our point of view, we are committed to making the same assumption about every other plausible point of view. Similarly, in the context of set theory, the authors propose the Copernican Principle as the constraint that for every assumption introduced by a multiverse theorist, s/he is committed to that it holds from the vantage point of an arbitrary universe of sets. The name is borrowed from a modern principle in physics, which Peacock states as “that humans are not privileged observers.” Peacock applies the principle arguing “if the universe appears isotropic about our position, it would also appear isotropic to observers in other galaxies” [Reference Peacock16, p. 66]. So for the physicist, the principle is a conceivably falsifiable statement about the uniformity of the physical universe; while for the theorist of the multiverse of sets, it is an a priori postulate. Below we explicate a formal deductive rule,
![]() $\mathsf {NEC}$
, expressing this principle.
$\mathsf {NEC}$
, expressing this principle.
To approach the Main Question, we require a framework that makes sense of the notion of truth-in-a-universe. If the universes are mere models of
![]() $\mathsf {ZF}$
, then the usual satisfaction-relation expressed in the language of set theory suffices. But as soon as we consider each universe to contain a multiverse in its own right, it is more natural to consider the universes as structures in the language of the multiverse theory.
$\mathsf {ZF}$
, then the usual satisfaction-relation expressed in the language of set theory suffices. But as soon as we consider each universe to contain a multiverse in its own right, it is more natural to consider the universes as structures in the language of the multiverse theory.
The main contribution of this paper is an untyped framework for handling the notion of truth-in-a-
![]() $\mathsf {ZF}$
-universe. It is intended to be applicable to just about any theory of the multiverse of sets. A primitive predicate
$\mathsf {ZF}$
-universe. It is intended to be applicable to just about any theory of the multiverse of sets. A primitive predicate
![]() $\mathsf {Uni}(\mathcal {U})$
is introduced to express that
$\mathsf {Uni}(\mathcal {U})$
is introduced to express that
![]() $\mathcal {U}$
is a universe, and the primitive relation
$\mathcal {U}$
is a universe, and the primitive relation
![]() $\mathsf {Mod}(\mathcal {U}, \sigma )$
is introduced to express that the
$\mathsf {Mod}(\mathcal {U}, \sigma )$
is introduced to express that the
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-statement
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-statement
![]() $\sigma $
is true in the universe
$\sigma $
is true in the universe
![]() $\mathcal {U}$
, where
$\mathcal {U}$
, where
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
is the language of set theory,
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
is the language of set theory,
![]() $\mathcal {L}$
, augmented with the symbols
$\mathcal {L}$
, augmented with the symbols
![]() $\mathsf {Uni}$
and
$\mathsf {Uni}$
and
![]() $\mathsf {Mod}$
. The multiverse theories considered in this paper are expressed in
$\mathsf {Mod}$
. The multiverse theories considered in this paper are expressed in
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
.
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
.
1.1 Multiverse principles
Now that the language
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
and the intuitive intended meaning of its symbols have been briefly explained, the next task is to give natural and useful axioms for
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
and the intuitive intended meaning of its symbols have been briefly explained, the next task is to give natural and useful axioms for
![]() $\mathsf {Uni}$
and
$\mathsf {Uni}$
and
![]() $\mathsf {Mod}$
. Axioms for
$\mathsf {Mod}$
. Axioms for
![]() $\mathsf {Uni}$
specify what universes comprise the multiverse, what closure properties it satisfies, etc.; for example the multiverse axioms of [Reference Hamkins12]. In this paper we are focused on semantically motivated axioms, meant to be applicable to a wide range of multiverse conceptions. The application of this framework to Hamkins’s multiverse is discussed in Section 6.2. Since
$\mathsf {Uni}$
specify what universes comprise the multiverse, what closure properties it satisfies, etc.; for example the multiverse axioms of [Reference Hamkins12]. In this paper we are focused on semantically motivated axioms, meant to be applicable to a wide range of multiverse conceptions. The application of this framework to Hamkins’s multiverse is discussed in Section 6.2. Since
![]() $\mathsf {Mod}$
is an untyped semantic relation, it is not surprising that it is exposed to liar-style phenomena. Our Theorem 4.6 shows, e.g., that the schema
$\mathsf {Mod}$
is an untyped semantic relation, it is not surprising that it is exposed to liar-style phenomena. Our Theorem 4.6 shows, e.g., that the schema
![]() $\big ( \forall \mathcal {U} \hspace {2pt} (\mathsf {Uni}(\mathcal {U}) \rightarrow \mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner ) \big ) \rightarrow \sigma $
, over
$\big ( \forall \mathcal {U} \hspace {2pt} (\mathsf {Uni}(\mathcal {U}) \rightarrow \mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner ) \big ) \rightarrow \sigma $
, over
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-statements
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-statements
![]() $\sigma $
, expressing that whatever holds in every universe also holds in the background universe, is inconsistent with a natural and mild theory in
$\sigma $
, expressing that whatever holds in every universe also holds in the background universe, is inconsistent with a natural and mild theory in
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
. However, this contradiction is not derivable when this schema is restricted to
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
. However, this contradiction is not derivable when this schema is restricted to
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
The basic theory introduced is called
![]() $\mathsf {CM}^-$
(Compositional satisfaction for the Multiverse).Footnote
3
$\mathsf {CM}^-$
(Compositional satisfaction for the Multiverse).Footnote
3
![]() $\mathsf {CM}^-$
is formed by adding compositional semantically motivated
$\mathsf {CM}^-$
is formed by adding compositional semantically motivated
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-axioms to the background theory
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-axioms to the background theory
![]() $\mathsf {ZF}$
, for each logical connective and quantifier, and by extending the Separation and Replacement schemas of
$\mathsf {ZF}$
, for each logical connective and quantifier, and by extending the Separation and Replacement schemas of
![]() $\mathsf {ZF}$
to
$\mathsf {ZF}$
to
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
. For example, the compositional axiom for
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
. For example, the compositional axiom for
![]() $\wedge $
is
$\wedge $
is
These are also called the Tarskian laws of satisfaction. The analogue in the present framework of the well-known Tarskian schema
![]() $\mathsf {Tr}(\ulcorner \sigma \urcorner ) \leftrightarrow \sigma $
(for
$\mathsf {Tr}(\ulcorner \sigma \urcorner ) \leftrightarrow \sigma $
(for
![]() $\sigma \in \mathcal {L}$
) would say roughly that
$\sigma \in \mathcal {L}$
) would say roughly that
![]() $\sigma $
is true in every universe if, and only if, it holds in the background universe. So this would say that the multiverse is not very diverse, and certainly not closed under forcing, for example. But analogues of
$\sigma $
is true in every universe if, and only if, it holds in the background universe. So this would say that the multiverse is not very diverse, and certainly not closed under forcing, for example. But analogues of
![]() $\mathsf {Tr}(\ulcorner \sigma \urcorner ) \rightarrow \sigma $
(for
$\mathsf {Tr}(\ulcorner \sigma \urcorner ) \rightarrow \sigma $
(for
![]() $\sigma \in \mathcal {L}$
) and the rule of Necessitation
$\sigma \in \mathcal {L}$
) and the rule of Necessitation
![]() $\vdash \sigma \Rightarrow \hspace {2pt} \vdash \mathsf {Tr}(\ulcorner \sigma \urcorner )$
(for
$\vdash \sigma \Rightarrow \hspace {2pt} \vdash \mathsf {Tr}(\ulcorner \sigma \urcorner )$
(for
![]() $\sigma \in \mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
) are highly relevant.
$\sigma \in \mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
) are highly relevant.
In
![]() $\mathsf {CM}^-$
we can prove the soundness principle that the set of statements true in any particular universe is deductively closed.
$\mathsf {CM}^-$
we can prove the soundness principle that the set of statements true in any particular universe is deductively closed.
![]() $\mathsf {CM}$
is
$\mathsf {CM}$
is
![]() $\mathsf {CM}^-$
plus an axiom called
$\mathsf {CM}^-$
plus an axiom called
![]() $\textsf {Multiverse}_{\mathsf {ZF}}$
saying that every universe satisfies
$\textsf {Multiverse}_{\mathsf {ZF}}$
saying that every universe satisfies
![]() $\mathsf {ZF}$
, which is just intended to set the scope of the present treatment. (For most of the results, the authors believe that natural generalizations to weak fragments of
$\mathsf {ZF}$
, which is just intended to set the scope of the present treatment. (For most of the results, the authors believe that natural generalizations to weak fragments of
![]() $\mathsf {ZF}$
are possible.) Theorem 5.6 shows that an extension of
$\mathsf {ZF}$
are possible.) Theorem 5.6 shows that an extension of
![]() $\mathsf {CM}$
interpreting the Gödel–Löb modal logic is conservative over
$\mathsf {CM}$
interpreting the Gödel–Löb modal logic is conservative over
![]() $\mathsf {ZF}$
. So by the soundness principle,
$\mathsf {ZF}$
. So by the soundness principle,
![]() $\textsf {Multiverse}_{\mathsf {ZF}}$
, and Gödel’s second incompleteness theorem,
$\textsf {Multiverse}_{\mathsf {ZF}}$
, and Gödel’s second incompleteness theorem,
![]() $\mathsf {CM}$
does not prove the statement
$\mathsf {CM}$
does not prove the statement
![]() $\exists \mathcal {U} \hspace {2pt} \mathsf {Uni}(\mathcal {U})$
, saying that there exists a universe.
$\exists \mathcal {U} \hspace {2pt} \mathsf {Uni}(\mathcal {U})$
, saying that there exists a universe.
A flexible revision-semantic technique for expanding models of the background theory
![]() $\mathsf {ZF}$
to models of extensions of
$\mathsf {ZF}$
to models of extensions of
![]() $\mathsf {CM}^-$
is developed. This technique builds on ideas from [Reference Gupta9], for circumventing truth-theoretic paradoxes. In short, one starts by setting parameters specifying the particular multiverse conception desired. Among other things, this pins down the interpretation of
$\mathsf {CM}^-$
is developed. This technique builds on ideas from [Reference Gupta9], for circumventing truth-theoretic paradoxes. In short, one starts by setting parameters specifying the particular multiverse conception desired. Among other things, this pins down the interpretation of
![]() $\mathsf {Uni}$
. Then the interpretation of
$\mathsf {Uni}$
. Then the interpretation of
![]() $\mathsf {Mod}$
is determined by a revision-semantic process. Intuitively, a basic definition of truth-in-a-universe is supplied among the parameters, and this definition is revised step-by-step to more adequate definitions. Theorems 5.4 and 5.5 show that some natural settings of the parameters lead to that further semantically motivated axioms and deductive rules are validated in the constructed model, more on this further below.
$\mathsf {Mod}$
is determined by a revision-semantic process. Intuitively, a basic definition of truth-in-a-universe is supplied among the parameters, and this definition is revised step-by-step to more adequate definitions. Theorems 5.4 and 5.5 show that some natural settings of the parameters lead to that further semantically motivated axioms and deductive rules are validated in the constructed model, more on this further below.
We introduce several axioms and deductive rules in response to the Main Question. The most fundamental such principle for this framework is the deductive rule of Necessitation,
![]() $\mathsf {NEC}$
, which is a formal expression of the Copernican Principle:
$\mathsf {NEC}$
, which is a formal expression of the Copernican Principle:
where
![]() $\ulcorner \sigma \urcorner $
is the Gödel code of
$\ulcorner \sigma \urcorner $
is the Gödel code of
![]() $\sigma $
. Under mild assumptions on the parameters,
$\sigma $
. Under mild assumptions on the parameters,
![]() $\mathsf {NEC}$
is validated in the revision-semantic model construction. Theorem 4.8 shows that
$\mathsf {NEC}$
is validated in the revision-semantic model construction. Theorem 4.8 shows that
![]() $\mathsf {CM} + \mathsf {NEC}$
is conservative over
$\mathsf {CM} + \mathsf {NEC}$
is conservative over
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Dually, the deductive rule of Co-Necessitation,
![]() $\mathsf {CONEC}$
, states:
$\mathsf {CONEC}$
, states:
In the context of
![]() $\mathsf {NEC}$
as formalizing the Copernican Principle,
$\mathsf {NEC}$
as formalizing the Copernican Principle,
![]() $\mathsf {CONEC}$
may be thought of as expressing that the theory is maximal within the bounds of the Copernican Principle. On the other hand, as a stand-alone principle,
$\mathsf {CONEC}$
may be thought of as expressing that the theory is maximal within the bounds of the Copernican Principle. On the other hand, as a stand-alone principle,
![]() $\mathsf {CONEC}$
can be used to boost the expressive power: For example, we will consider
$\mathsf {CONEC}$
can be used to boost the expressive power: For example, we will consider
![]() $\mathsf {CM}$
extended by
$\mathsf {CM}$
extended by
![]() $\mathsf {CONEC}$
and the statement that no universe satisfies a
$\mathsf {CONEC}$
and the statement that no universe satisfies a
![]() $\Sigma ^0_1$
-statement that does not already hold in the standard model of arithmetic in the background theory; in other words, a Turing machine that does not halt in the background theory, halts in no universe. In
$\Sigma ^0_1$
-statement that does not already hold in the standard model of arithmetic in the background theory; in other words, a Turing machine that does not halt in the background theory, halts in no universe. In
![]() $\mathsf {CM}$
extended with this axiom we can use basic model-theoretic considerations to prove that every universe satisfies the Reflection schema iterated
$\mathsf {CM}$
extended with this axiom we can use basic model-theoretic considerations to prove that every universe satisfies the Reflection schema iterated
![]() $\omega ^{\textrm {CK}}_1$
times over
$\omega ^{\textrm {CK}}_1$
times over
![]() $\mathsf {ZF}$
.Footnote
4
Now, by adding
$\mathsf {ZF}$
.Footnote
4
Now, by adding
![]() $\mathsf {CONEC}$
we can prove
$\mathsf {CONEC}$
we can prove
![]() $\omega ^{\textrm {CK}}_1$
-iterated Reflection schema over
$\omega ^{\textrm {CK}}_1$
-iterated Reflection schema over
![]() $\mathsf {ZF}$
outright in the background theory. So in general,
$\mathsf {ZF}$
outright in the background theory. So in general,
![]() $\mathsf {CONEC}$
enables outright proofs of statements that are provably satisfied across a model-theoretically delimited multiverse, thus in some sense “extracting the deductively accessible content” of higher-order non-recursive properties.
$\mathsf {CONEC}$
enables outright proofs of statements that are provably satisfied across a model-theoretically delimited multiverse, thus in some sense “extracting the deductively accessible content” of higher-order non-recursive properties.
We write
![]() $\mathsf {MS}$
(Multiverse theory of Satisfaction) for the theory
$\mathsf {MS}$
(Multiverse theory of Satisfaction) for the theory
![]() $\mathsf {CM} + \mathsf {NEC} + \mathsf {CONEC}$
. This theory is analogous to the Firedman–Sheard theory of truth (
$\mathsf {CM} + \mathsf {NEC} + \mathsf {CONEC}$
. This theory is analogous to the Firedman–Sheard theory of truth (
![]() $\mathsf {FS}$
) from [Reference Friedman and Sheard5]. A revision-semantic technique for constructing models of
$\mathsf {FS}$
) from [Reference Friedman and Sheard5]. A revision-semantic technique for constructing models of
![]() $\mathsf {CM} + \mathsf {NEC} \text { and/or } \mathsf {CONEC}$
(building on a technique from the aforementioned two papers) is embodied in the Main Lemma (in Section 5) and its Corollary 5.2.
$\mathsf {CM} + \mathsf {NEC} \text { and/or } \mathsf {CONEC}$
(building on a technique from the aforementioned two papers) is embodied in the Main Lemma (in Section 5) and its Corollary 5.2.
We now proceed to discuss three axioms motivated by the Main Question that have a reflective character in that they assert that the background universe is in some sense reflected in the multiverse. We will establish bounds on the consistency strength of these in terms of iterated reflection principles. The reader is referred to Systems 2.8 and 5.3 for the definition of these principles.
A very basic multiverse axiom is
![]() $\textsf {Non-Triviality}$
,
$\textsf {Non-Triviality}$
,
![]() $\exists \mathcal {U} \hspace {2pt} \mathsf {Uni}(\mathcal {U})$
, saying that there is a universe. In the presence of
$\exists \mathcal {U} \hspace {2pt} \mathsf {Uni}(\mathcal {U})$
, saying that there is a universe. In the presence of
![]() $\mathsf {NEC}$
, this also yields that every universe contains a universe, and so on. We show in Theorem 5.4 (and in Theorem 5.6) that
$\mathsf {NEC}$
, this also yields that every universe contains a universe, and so on. We show in Theorem 5.4 (and in Theorem 5.6) that
![]() $\mathsf {CM} + \textsf {Non-Triviality} + \mathsf {NEC}$
is locally interpreted in (and conservative over) the theory of iterated consistency over
$\mathsf {CM} + \textsf {Non-Triviality} + \mathsf {NEC}$
is locally interpreted in (and conservative over) the theory of iterated consistency over
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
A stronger axiom motivated by the Main Question, called
![]() $\textsf {Self-Perception}$
, expresses that the background universe is isomorphic (over the set theoretic language) to one of the internal universes. This embodies the idea that the universe of the background theory should also be available in its internal multiverse, and has a distinct reflective character. It turns out to be convenient to take the universes to be countable recursively saturated models when modeling
$\textsf {Self-Perception}$
, expresses that the background universe is isomorphic (over the set theoretic language) to one of the internal universes. This embodies the idea that the universe of the background theory should also be available in its internal multiverse, and has a distinct reflective character. It turns out to be convenient to take the universes to be countable recursively saturated models when modeling
![]() $\mathsf {CM} + \textsf {Self-Perception} + \mathsf {NEC}$
, a phenomenon that corresponds to the multiverse model of Gitman and Hamkins in [Reference Gitman and Hamkins7]. This suggests that their multiverse theory would harmonize well with
$\mathsf {CM} + \textsf {Self-Perception} + \mathsf {NEC}$
, a phenomenon that corresponds to the multiverse model of Gitman and Hamkins in [Reference Gitman and Hamkins7]. This suggests that their multiverse theory would harmonize well with
![]() $\mathsf {CM} + \textsf {Self-Perception} + \mathsf {NEC}$
, a hypothesis we explore briefly in Section 6.2. In Theorem 5.7, we use the revision-semantic technique to interpret
$\mathsf {CM} + \textsf {Self-Perception} + \mathsf {NEC}$
, a hypothesis we explore briefly in Section 6.2. In Theorem 5.7, we use the revision-semantic technique to interpret
![]() $\mathsf {CM} + \textsf {Self-Perception} + \mathsf {NEC}$
in the theory of
$\mathsf {CM} + \textsf {Self-Perception} + \mathsf {NEC}$
in the theory of
![]() $\omega $
-iterated Global Reflection over
$\omega $
-iterated Global Reflection over
![]() $\mathsf {ZF}$
. The latter is a natural untyped theory of truth, that mildly strengthens
$\mathsf {ZF}$
. The latter is a natural untyped theory of truth, that mildly strengthens
![]() $\mathsf {ZF}$
. All universes are countable recursively saturated in this interpretation.
$\mathsf {ZF}$
. All universes are countable recursively saturated in this interpretation.
![]() $\textsf {Self-Perception}$
is closely related to the notion of condensible models studied by Enayat in [Reference Enayat3]. The definition of condensability is somewhat technical, involving an infinitary language: A model
$\textsf {Self-Perception}$
is closely related to the notion of condensible models studied by Enayat in [Reference Enayat3]. The definition of condensability is somewhat technical, involving an infinitary language: A model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathsf {ZF}$
is condensible, if there is some ordinal
$\mathsf {ZF}$
is condensible, if there is some ordinal
![]() $\alpha \in \mathcal {M}$
such that
$\alpha \in \mathcal {M}$
such that
![]() $\mathcal {M} \cong \mathcal {M}(\alpha ) \prec _{\mathbb {L}_{\mathcal {M}}} \mathcal {M}$
, where
$\mathcal {M} \cong \mathcal {M}(\alpha ) \prec _{\mathbb {L}_{\mathcal {M}}} \mathcal {M}$
, where
![]() $\mathcal {M}(\alpha )$
denotes the substructure of
$\mathcal {M}(\alpha )$
denotes the substructure of
![]() $\mathcal {M}$
of ranks below
$\mathcal {M}$
of ranks below
![]() $\alpha $
and
$\alpha $
and
![]() $\mathbb {L}_{\mathcal {M}}$
denotes the intersection of
$\mathbb {L}_{\mathcal {M}}$
denotes the intersection of
![]() $\mathcal {L}_{\omega _1, \omega }$
with the well-founded part of
$\mathcal {L}_{\omega _1, \omega }$
with the well-founded part of
![]() $\mathcal {M}$
. In particular, Enayat positively answers a question that sprung from the present paper: Is there an
$\mathcal {M}$
. In particular, Enayat positively answers a question that sprung from the present paper: Is there an
![]() $\omega $
-standard model of
$\omega $
-standard model of
![]() $\mathsf {ZF}$
with unboundedly many ordinals
$\mathsf {ZF}$
with unboundedly many ordinals
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathcal {M} \cong \mathcal {M}(\alpha ) \prec \mathcal {M}$
? Note that recursively saturated models are
$\mathcal {M} \cong \mathcal {M}(\alpha ) \prec \mathcal {M}$
? Note that recursively saturated models are
![]() $\omega $
-non-standard. Enayat’s result means that the door also appears to be open for models of
$\omega $
-non-standard. Enayat’s result means that the door also appears to be open for models of
![]() $\mathsf {CM} + \textsf {Self-Perception} + \mathsf {NEC}$
with
$\mathsf {CM} + \textsf {Self-Perception} + \mathsf {NEC}$
with
![]() $\omega $
-standard universes.
$\omega $
-standard universes.
We also introduce the axiom schema of
![]() $\textsf {Multiverse Reflection}$
, stating for each sentence
$\textsf {Multiverse Reflection}$
, stating for each sentence
![]() $\sigma $
in the language
$\sigma $
in the language
![]() $\mathcal {L}$
of set theory:
$\mathcal {L}$
of set theory:
![]() $\big ( \forall \mathcal {U} \hspace {2pt} (\mathsf {Uni}(\mathcal {U}) \rightarrow \mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner )) \big ) \rightarrow \sigma $
. Over
$\big ( \forall \mathcal {U} \hspace {2pt} (\mathsf {Uni}(\mathcal {U}) \rightarrow \mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner )) \big ) \rightarrow \sigma $
. Over
![]() $\mathsf {CM}$
, this principle is implied by
$\mathsf {CM}$
, this principle is implied by
![]() $\textsf {Self-Perception}$
and implies
$\textsf {Self-Perception}$
and implies
![]() $\textsf {Non-Triviality}$
. Using the revision-semantic technique, we show in Theorem 5.5 (and in Theorem 5.6) that
$\textsf {Non-Triviality}$
. Using the revision-semantic technique, we show in Theorem 5.5 (and in Theorem 5.6) that
![]() $\mathsf {MS} + \textsf {Multiverse Reflection}$
is locally interpreted in (and conservative over) the theory of
$\mathsf {MS} + \textsf {Multiverse Reflection}$
is locally interpreted in (and conservative over) the theory of
![]() $\omega $
-iterated proof-theoretic reflection schema over
$\omega $
-iterated proof-theoretic reflection schema over
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
The body of the paper ends with case studies, where we look at two independent multiverse conceptions through the lens of the framework we have developed. The first of these is a conception of the multiverse as being arithmetically absolute, in the sense that arithmetic truth does not vary across the multiverse. The second is a conception due to Hamkins which is fundamentally based on the principles that the multiverse is closed under the forcing and inner model techniques, and that every universe is countable and
![]() $\omega $
-non-standard from the perspective of some other universe. We close with a concluding section reflecting on the contributions of the paper and the relevance of this framework for future research on the set-theoretic multiverse.
$\omega $
-non-standard from the perspective of some other universe. We close with a concluding section reflecting on the contributions of the paper and the relevance of this framework for future research on the set-theoretic multiverse.
2 Preliminaries
2.1 A term-calculus for representation of syntax
We shall work with various recursively enumerable set theories, in languages obtained by adding finitely many new non-logical symbols to the usual language of set theory on the signature
![]() $\{\in \}$
. We define a set theory to be any recursively enumerable system proving Mac Lane set theory (excluding Choice)Footnote
5
or proving Kripke–Platek set theory with Infinity,Footnote
6
in a language with finitely many non-logical symbols including a term-calculus for arithmetic and Gödel coding explained below. Our specific choice of set theories underlying this definition is somewhat arbitrary (even weaker theories may well suffice). Both of these theories are sufficient for constructing the structure of the natural numbers and implementing basic model theory; these are the important features for this paper.
$\{\in \}$
. We define a set theory to be any recursively enumerable system proving Mac Lane set theory (excluding Choice)Footnote
5
or proving Kripke–Platek set theory with Infinity,Footnote
6
in a language with finitely many non-logical symbols including a term-calculus for arithmetic and Gödel coding explained below. Our specific choice of set theories underlying this definition is somewhat arbitrary (even weaker theories may well suffice). Both of these theories are sufficient for constructing the structure of the natural numbers and implementing basic model theory; these are the important features for this paper.
Since we will be reasoning about syntactic objects, it is convenient to employ a Gödel coding of syntax. Let K be a language with finitely many non-logical symbols. In any set theory T (in language L) under consideration, we can define the arithmetic functions needed to formulate a natural Gödel coding in T of terms and formulas of K. Through the Gödel coding, the “grammatical structure” of K is coherently represented in T. The complicated details of this procedure are described in any rigorous account of Gödel’s incompleteness theorems. The gist is that for each syntactic object (symbol, term or formula) s of K, there is a definable number
![]() $\ulcorner s \urcorner $
in L (the Gödel code of s), which represents s in T, and there are operations definable in T corresponding to syntactic operations on such objects. The authors trust that the reader is familiar with this.
$\ulcorner s \urcorner $
in L (the Gödel code of s), which represents s in T, and there are operations definable in T corresponding to syntactic operations on such objects. The authors trust that the reader is familiar with this.
It is customary in set theory to informally introduce defined constant, relation and function symbols to the language, in order to make the presentation more readable. For example, one may use a function symbol
![]() $+$
, as if it belonged to the language and there was an axiom expressing that
$+$
, as if it belonged to the language and there was an axiom expressing that
![]() $+$
is addition on the finite von Neumann ordinals. In this paper we assume that a finite number of such symbols needed for arithmetic and Gödel coding are already present in the language of every set theory, and that the appropriate axioms regulating them are available in every set theory. Here follows a semi-formal account of some of the main principles of this expanded language L for a set theory T, also serving to specify the notation:
$+$
is addition on the finite von Neumann ordinals. In this paper we assume that a finite number of such symbols needed for arithmetic and Gödel coding are already present in the language of every set theory, and that the appropriate axioms regulating them are available in every set theory. Here follows a semi-formal account of some of the main principles of this expanded language L for a set theory T, also serving to specify the notation:
-
1. We have a constant
 $\underline {0}$
and function symbols
$\underline {0}$
and function symbols
 $S, +, \times $
for the successor, addition and multiplication operations in arithmetic. For each
$S, +, \times $
for the successor, addition and multiplication operations in arithmetic. For each
 $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $\underline {n}$
is shorthand for
$\underline {n}$
is shorthand for
 $S^n(\underline {0})$
.
$S^n(\underline {0})$
. -
2. Each variable, constant, relation or function symbol s of K is represented in T by a numeral
 $\ulcorner s \urcorner $
in L.
$\ulcorner s \urcorner $
in L. -
3. Recursively, each term
 $f(t_1, \dots , t_n)$
of K is represented by the term
$f(t_1, \dots , t_n)$
of K is represented by the term
 $\ulcorner f \urcorner (\ulcorner t_1 \urcorner , \dots , \ulcorner t_n \urcorner )$
of L. Formally, the term
$\ulcorner f \urcorner (\ulcorner t_1 \urcorner , \dots , \ulcorner t_n \urcorner )$
of L. Formally, the term
 $\ulcorner f \urcorner (\ulcorner t_1 \urcorner , \dots , \ulcorner t_n \urcorner )$
is the result of applying a function symbol of L to the numerals
$\ulcorner f \urcorner (\ulcorner t_1 \urcorner , \dots , \ulcorner t_n \urcorner )$
is the result of applying a function symbol of L to the numerals
 $\ulcorner f \urcorner , \ulcorner t_1 \urcorner , \dots , \ulcorner t_n \urcorner $
. Moreover,
$\ulcorner f \urcorner , \ulcorner t_1 \urcorner , \dots , \ulcorner t_n \urcorner $
. Moreover,
 $\ulcorner f(t_1, \dots , t_n) \urcorner $
denotes a numeral that T proves to equal
$\ulcorner f(t_1, \dots , t_n) \urcorner $
denotes a numeral that T proves to equal
 $\ulcorner f \urcorner (\ulcorner t_1 \urcorner , \dots , \ulcorner t_n \urcorner )$
.
$\ulcorner f \urcorner (\ulcorner t_1 \urcorner , \dots , \ulcorner t_n \urcorner )$
. -
4. Each atomic formula
 $R(t_1, \dots , t_n)$
of K is represented by the numeral
$R(t_1, \dots , t_n)$
of K is represented by the numeral
 $\ulcorner R(t_0, \dots , t_n) \urcorner $
of L. Analogous remarks apply as in the case of terms described above.
$\ulcorner R(t_0, \dots , t_n) \urcorner $
of L. Analogous remarks apply as in the case of terms described above. -
5. The syntactic operations, standardly used to build up complex formulas from atomic formulas, are all available. For example:
-
(a) L has a function symbol
 $\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }}$
, such that for each
$\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }}$
, such that for each
 $\phi $
in K,
$\phi $
in K,
 $\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }} \ulcorner \phi \urcorner $
represents
$\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }} \ulcorner \phi \urcorner $
represents
 $\neg \phi $
. Moreover, T proves that
$\neg \phi $
. Moreover, T proves that
 $\ulcorner \neg \phi \urcorner =\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }} \ulcorner \phi \urcorner $
.
$\ulcorner \neg \phi \urcorner =\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }} \ulcorner \phi \urcorner $
. -
(b) L has a function symbol
 $\mathrel {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\wedge }}$
, such that for each
$\mathrel {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\wedge }}$
, such that for each
 $\phi $
and each
$\phi $
and each
 $\psi $
in K,
$\psi $
in K,
 $\ulcorner \phi \urcorner \mathrel {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\wedge }} \ulcorner \psi \urcorner $
represents
$\ulcorner \phi \urcorner \mathrel {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\wedge }} \ulcorner \psi \urcorner $
represents
 $\phi \wedge \psi $
. Moreover, T proves that
$\phi \wedge \psi $
. Moreover, T proves that
 $\ulcorner \phi \wedge \psi \urcorner =\ulcorner \phi \urcorner \mathrel {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\wedge }} \ulcorner \psi \urcorner $
.
$\ulcorner \phi \wedge \psi \urcorner =\ulcorner \phi \urcorner \mathrel {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\wedge }} \ulcorner \psi \urcorner $
. -
(c) L has a function symbol
 $\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\forall }}$
, such that for each variable v and each formula
$\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\forall }}$
, such that for each variable v and each formula
 $\phi $
in K,
$\phi $
in K,
 $\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\forall }} \ulcorner v \urcorner \hspace {2pt} \ulcorner \phi \urcorner $
represents
$\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\forall }} \ulcorner v \urcorner \hspace {2pt} \ulcorner \phi \urcorner $
represents
 $\forall v \hspace {2pt} \phi $
. Moreover, T proves that
$\forall v \hspace {2pt} \phi $
. Moreover, T proves that
 $\ulcorner \forall v \hspace {2pt} \phi \urcorner =\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\forall }} \ulcorner v \urcorner \hspace {2pt} \ulcorner \phi \urcorner $
.
$\ulcorner \forall v \hspace {2pt} \phi \urcorner =\mathop {\underset {\substack {\\[-9.5pt]\mbox {.}}}{\forall }} \ulcorner v \urcorner \hspace {2pt} \ulcorner \phi \urcorner $
. -
(d) For any
 $\phi $
in K,
$\phi $
in K,
 $\phi [t/x]$
denotes the formula obtained from
$\phi [t/x]$
denotes the formula obtained from
 $\phi $
by replacing each free occurrence of the variable x by the term t (if t has variables, then their bound occurrences in
$\phi $
by replacing each free occurrence of the variable x by the term t (if t has variables, then their bound occurrences in
 $\phi $
are renamed as necessary). L has a function symbol (written
$\phi $
are renamed as necessary). L has a function symbol (written
 $-[-\underset {\substack {\\[-9.5pt]\mbox {.}}}{/}-]$
) which represents this primitive recursive substitution operation. Moreover, T proves that
$-[-\underset {\substack {\\[-9.5pt]\mbox {.}}}{/}-]$
) which represents this primitive recursive substitution operation. Moreover, T proves that
 $\ulcorner \phi (x)[y/x] \urcorner = \ulcorner \phi (x) \urcorner [\ulcorner y \urcorner \underset {\substack {\\[-9.5pt]\mbox {.}}}{/}\ulcorner x \urcorner ]$
. Somewhat less formally, if
$\ulcorner \phi (x)[y/x] \urcorner = \ulcorner \phi (x) \urcorner [\ulcorner y \urcorner \underset {\substack {\\[-9.5pt]\mbox {.}}}{/}\ulcorner x \urcorner ]$
. Somewhat less formally, if
 $\phi $
has been introduced as
$\phi $
has been introduced as
 $\phi (x)$
, we may write
$\phi (x)$
, we may write
 $\phi (t)$
for the formula
$\phi (t)$
for the formula
 $\phi [t/x]$
.
$\phi [t/x]$
.
-
In the context of a set theory T in a set-theoretic language L,
![]() $\Sigma ^0_n$
,
$\Sigma ^0_n$
,
![]() $\Pi ^0_n$
and
$\Pi ^0_n$
and
![]() $\Delta ^0_n$
denote the usual arithmetic hierarchy as defined for L-formulas (all quantifiers are bounded to
$\Delta ^0_n$
denote the usual arithmetic hierarchy as defined for L-formulas (all quantifiers are bounded to
![]() $\mathbb {N}$
), up to equivalence in T. It is well-known that for any recursive system S, there is a
$\mathbb {N}$
), up to equivalence in T. It is well-known that for any recursive system S, there is a
![]() $\Sigma ^0_1$
-formula
$\Sigma ^0_1$
-formula
![]() $\Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{S}}$
, representing S-provability in T. We write
$\Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{S}}$
, representing S-provability in T. We write
![]() $\mathrm {Con}_{\underset {\substack {\\[-9.5pt]\mbox {.}}}{S}}$
for the sentence
$\mathrm {Con}_{\underset {\substack {\\[-9.5pt]\mbox {.}}}{S}}$
for the sentence
![]() $\neg \Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{S}}(\ulcorner \bot ) \urcorner $
, expressing that S is consistent. In both cases, the dot under S is sometimes omitted, when it can be inferred from the context.
$\neg \Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{S}}(\ulcorner \bot ) \urcorner $
, expressing that S is consistent. In both cases, the dot under S is sometimes omitted, when it can be inferred from the context.
As an example, consider this consequence of Gödel’s second incompleteness theorem:
From the perspective of the meta-theory, “
![]() $\mathsf {ZF}$
” refers to a set of sentences (the object theory of
$\mathsf {ZF}$
” refers to a set of sentences (the object theory of
![]() $\mathsf {ZF}$
) whereas “
$\mathsf {ZF}$
) whereas “
![]() $\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {ZF}}$
” refers to a formula representing the recursive set of Gödel codes of that set in the object theory
$\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {ZF}}$
” refers to a formula representing the recursive set of Gödel codes of that set in the object theory
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Suppose now that a set theory
![]() $T^{\prime }$
in language
$T^{\prime }$
in language
![]() $L^{\prime }$
is represented in a set theory T in language L. Then
$L^{\prime }$
is represented in a set theory T in language L. Then
![]() $L^{\prime }$
is Gödel coded in T, as explained above. But
$L^{\prime }$
is Gödel coded in T, as explained above. But
![]() $T^{\prime }$
, in turn, also Gödel codes languages; say that
$T^{\prime }$
, in turn, also Gödel codes languages; say that
![]() $T^{\prime }$
Gödel codes the language
$T^{\prime }$
Gödel codes the language
![]() $L^{\prime \prime }$
. Note that the whole Gödel coding of
$L^{\prime \prime }$
. Note that the whole Gödel coding of
![]() $L^{\prime \prime }$
in
$L^{\prime \prime }$
in
![]() $T^{\prime }$
is then carried along by the representation of
$T^{\prime }$
is then carried along by the representation of
![]() $T^{\prime }$
in T. For example, if
$T^{\prime }$
in T. For example, if
![]() $\phi $
is a formula in
$\phi $
is a formula in
![]() $L^{\prime \prime }$
, then there is a term
$L^{\prime \prime }$
, then there is a term
![]() $\ulcorner \phi \urcorner $
in
$\ulcorner \phi \urcorner $
in
![]() $L^{\prime }$
which represents
$L^{\prime }$
which represents
![]() $\phi $
in
$\phi $
in
![]() $T^{\prime }$
. If
$T^{\prime }$
. If
![]() $\psi (x)$
is a formula of
$\psi (x)$
is a formula of
![]() $L^{\prime }$
, we can then form the formula
$L^{\prime }$
, we can then form the formula
![]() $\psi [\ulcorner \phi \urcorner / x]$
of
$\psi [\ulcorner \phi \urcorner / x]$
of
![]() $L^{\prime }$
. This formula, in turn, is represented in T by an L-term
$L^{\prime }$
. This formula, in turn, is represented in T by an L-term
![]() $\ulcorner \psi [\ulcorner \phi \urcorner / x] \urcorner $
. So if
$\ulcorner \psi [\ulcorner \phi \urcorner / x] \urcorner $
. So if
![]() $\theta (y)$
is an L-formula, we can form the L-formula
$\theta (y)$
is an L-formula, we can form the L-formula
![]() $\theta [\ulcorner \psi [\ulcorner \phi \urcorner / x] \urcorner / y]$
. Thus, Gödel codes may be nested, as a set theory represents a set theory, which in turn represents a language.
$\theta [\ulcorner \psi [\ulcorner \phi \urcorner / x] \urcorner / y]$
. Thus, Gödel codes may be nested, as a set theory represents a set theory, which in turn represents a language.
2.2 Miscellaneous logical preliminaries
![]() $\mathcal {L}$
is the language with the symbol “
$\mathcal {L}$
is the language with the symbol “
![]() $\in $
” along with a finite number of arithmetic and syntactic symbols as explained in Section 2.1. We assume that
$\in $
” along with a finite number of arithmetic and syntactic symbols as explained in Section 2.1. We assume that
![]() $\mathsf {ZF}$
is formulated as an
$\mathsf {ZF}$
is formulated as an
![]() $\mathcal {L}$
-theory, with the natural axioms for defining the arithmetic and syntactic symbols of
$\mathcal {L}$
-theory, with the natural axioms for defining the arithmetic and syntactic symbols of
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
![]() $\mathcal {L}^+$
denotes any extension of
$\mathcal {L}^+$
denotes any extension of
![]() $\mathcal {L}$
with a finite number of new symbols.
$\mathcal {L}$
with a finite number of new symbols.
If L is a language and
![]() $S_1, \ldots , S_n$
are symbols, then
$S_1, \ldots , S_n$
are symbols, then
![]() $L_{S_1, \ldots , S_n}$
denotes the language obtained by augmenting L with
$L_{S_1, \ldots , S_n}$
denotes the language obtained by augmenting L with
![]() $S_1, \ldots , S_n$
. The Separation schema applying to all formulas of a language L is denoted
$S_1, \ldots , S_n$
. The Separation schema applying to all formulas of a language L is denoted
![]() $\mathsf {Sep}(L)$
, and the Replacement schema applying to all formulas of a language L is denoted
$\mathsf {Sep}(L)$
, and the Replacement schema applying to all formulas of a language L is denoted
![]() $\mathsf {Rep}(L)$
.
$\mathsf {Rep}(L)$
.
Any set theory suffices as meta-theory. Suppose that in the meta-theory we consider a definable set
![]() $A = \{x \mid \phi (x)\}$
, such as a theory. We may then refer to the corresponding set within an object-theory, for example as follows: Using the symbol A somewhat ambiguously, we write a statement of the form
$A = \{x \mid \phi (x)\}$
, such as a theory. We may then refer to the corresponding set within an object-theory, for example as follows: Using the symbol A somewhat ambiguously, we write a statement of the form
![]() $\mathsf {ZF} \vdash \cdots \mathcal {M} \models \underset {\substack {\\[-9.5pt]\mbox {.}}}{A} \cdots $
for the more formally precise statement of the form
$\mathsf {ZF} \vdash \cdots \mathcal {M} \models \underset {\substack {\\[-9.5pt]\mbox {.}}}{A} \cdots $
for the more formally precise statement of the form
![]() $\mathsf {ZF} \vdash \cdots \exists X \hspace {2pt} \big ( \forall x (x \in X \leftrightarrow \phi (x)) \wedge \forall x \in X \hspace {2pt} (\mathcal {M} \models x) \big ) \cdots $
. The dot under A is occasionally omitted, when clear from the context. To illustrate, we might express a special case of Gödel’s completeness theorem within T as
$\mathsf {ZF} \vdash \cdots \exists X \hspace {2pt} \big ( \forall x (x \in X \leftrightarrow \phi (x)) \wedge \forall x \in X \hspace {2pt} (\mathcal {M} \models x) \big ) \cdots $
. The dot under A is occasionally omitted, when clear from the context. To illustrate, we might express a special case of Gödel’s completeness theorem within T as
![]() $T \vdash \big ( \mathrm {Con}_{{\mathsf {ZF}}} \leftrightarrow \exists \mathcal {M} (\mathcal {M} \models {\mathsf {ZF}}) \big )$
. We say that a theory
$T \vdash \big ( \mathrm {Con}_{{\mathsf {ZF}}} \leftrightarrow \exists \mathcal {M} (\mathcal {M} \models {\mathsf {ZF}}) \big )$
. We say that a theory
![]() $T_1$
bounds the consistency strength of (or has at least as high consistency strength as) a theory
$T_1$
bounds the consistency strength of (or has at least as high consistency strength as) a theory
![]() $T_0$
if the consistency of
$T_0$
if the consistency of
![]() $T_1$
implies the consistency of
$T_1$
implies the consistency of
![]() $T_0$
.
$T_0$
.
An interpretation
![]() $\mathcal {I}$
from a language
$\mathcal {I}$
from a language
![]() $L_0$
to a language
$L_0$
to a language
![]() $L_1$
is a function
$L_1$
is a function
![]() $\mathcal {I} : L_0 \rightarrow L_1$
which is generated (by structural recursion) from the non-logical symbols of
$\mathcal {I} : L_0 \rightarrow L_1$
which is generated (by structural recursion) from the non-logical symbols of
![]() $L_0$
. Moreover, we say that
$L_0$
. Moreover, we say that
![]() $\mathcal {I}$
interprets or validates the
$\mathcal {I}$
interprets or validates the
![]() $L_0$
-system
$L_0$
-system
![]() $T_0$
in the
$T_0$
in the
![]() $L_1$
-system
$L_1$
-system
![]() $T_1$
if for any
$T_1$
if for any
![]() $L_0$
-formula
$L_0$
-formula
![]() $\phi $
,
$\phi $
,
![]() $T_1 \vdash \mathcal {I}(\phi )$
whenever
$T_1 \vdash \mathcal {I}(\phi )$
whenever
![]() $T_0 \vdash \phi $
.
$T_0 \vdash \phi $
.
As default, we work with first-order languages and classical logic, but we will consider additional deductive rules (NEC and CONEC).
![]() $\phi \equiv \psi $
is the statement that
$\phi \equiv \psi $
is the statement that
![]() $\phi $
and
$\phi $
and
![]() $\psi $
are identical formulas. If S and T are systems in languages both including L, then
$\psi $
are identical formulas. If S and T are systems in languages both including L, then
![]() $S \equiv _L T$
is the statement that S and T have the same L-theorems. If S is a system involving deductive rules, and A is an axiom, then
$S \equiv _L T$
is the statement that S and T have the same L-theorems. If S is a system involving deductive rules, and A is an axiom, then
![]() $S + A$
denotes the natural extension of S in which these deductive rules may be applied to proofs also involving A. For example, in
$S + A$
denotes the natural extension of S in which these deductive rules may be applied to proofs also involving A. For example, in
![]() $\mathsf {MS} + \exists x \hspace {2pt} \mathsf {Uni}(x)$
, we may use
$\mathsf {MS} + \exists x \hspace {2pt} \mathsf {Uni}(x)$
, we may use
![]() $\mathsf {NEC}$
to derive
$\mathsf {NEC}$
to derive
![]() $\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} \mathsf {Mod}(\mathcal {U}, \ulcorner \exists x \hspace {2pt} \mathsf {Uni}(x) \urcorner )$
.
$\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} \mathsf {Mod}(\mathcal {U}, \ulcorner \exists x \hspace {2pt} \mathsf {Uni}(x) \urcorner )$
.
It is sometimes notationally convenient to introduce classes of the form
![]() $A = \{ x \mid \phi (x) \}$
(the class of all sets x such that
$A = \{ x \mid \phi (x) \}$
(the class of all sets x such that
![]() $\phi (x)$
), where
$\phi (x)$
), where
![]() $\phi $
is an
$\phi $
is an
![]() $\mathcal {L}^+$
-formula. Then
$\mathcal {L}^+$
-formula. Then
![]() $x \in A$
may be regarded as an alternative notation for
$x \in A$
may be regarded as an alternative notation for
![]() $\phi (x)$
. Thus, we have no need to specify a formal class theory. For example
$\phi (x)$
. Thus, we have no need to specify a formal class theory. For example
![]() $V = \{ x \mid \top \}$
is the class of all sets.
$V = \{ x \mid \top \}$
is the class of all sets.
Formally,
![]() $\mathrm {Var}$
is the set of variables
$\mathrm {Var}$
is the set of variables
![]() $\{{x}_1, {x}_2, \dots \}$
, indexed by the positive natural numbers. But we use other symbols informally (such as
$\{{x}_1, {x}_2, \dots \}$
, indexed by the positive natural numbers. But we use other symbols informally (such as
![]() $x, y, p, f, \mathcal {U}, \ldots $
) for variables as well.
$x, y, p, f, \mathcal {U}, \ldots $
) for variables as well.
![]() $\mathrm {VA}$
is the class of variable-assignments,
$\mathrm {VA}$
is the class of variable-assignments,
![]() $\{f \mid f : \mathrm {Var} \rightarrow V \}$
. If a is a set (or a structure), then
$\{f \mid f : \mathrm {Var} \rightarrow V \}$
. If a is a set (or a structure), then
![]() $\mathrm {VA}^a$
is the set
$\mathrm {VA}^a$
is the set
![]() $\{f \mid f : \mathrm {Var} \rightarrow a\}$
of all variable-assignments to elements of (the underlying set of) a. If f is a variable-assignment and v is a variable, then
$\{f \mid f : \mathrm {Var} \rightarrow a\}$
of all variable-assignments to elements of (the underlying set of) a. If f is a variable-assignment and v is a variable, then
![]() $\mathrm {VA}_{f, v}$
is the set of all variable-assignments g, such that for all
$\mathrm {VA}_{f, v}$
is the set of all variable-assignments g, such that for all
![]() $u \in \mathrm {Var}$
,
$u \in \mathrm {Var}$
,
![]() $u \neq v \rightarrow g(u) = f(u)$
. Suppose that we are working in a set theory T in a language L containing terms
$u \neq v \rightarrow g(u) = f(u)$
. Suppose that we are working in a set theory T in a language L containing terms
![]() $t_1, \ldots t_n$
. Note that for
$t_1, \ldots t_n$
. Note that for
![]() $n < \omega $
, T proves from
$n < \omega $
, T proves from
![]() $v_1 \in \mathrm {Var}, \ldots , v_n \in \mathrm {Var}$
that there is a primitive recursive variable-assignment f satisfying
$v_1 \in \mathrm {Var}, \ldots , v_n \in \mathrm {Var}$
that there is a primitive recursive variable-assignment f satisfying
![]() $f(v_1) = t_1, \ldots , f(v_n) = t_n$
, and
$f(v_1) = t_1, \ldots , f(v_n) = t_n$
, and
![]() $\forall m \in \mathbb {N} \hspace {2pt} (m> n \rightarrow f(v_m) = \underline {0})$
. Such a variable assignment f is denoted
$\forall m \in \mathbb {N} \hspace {2pt} (m> n \rightarrow f(v_m) = \underline {0})$
. Such a variable assignment f is denoted
![]() $\langle v_1, \dots v_n \rangle \mapsto \langle t_1, \ldots t_n \rangle $
(or just
$\langle v_1, \dots v_n \rangle \mapsto \langle t_1, \ldots t_n \rangle $
(or just
![]() $v_1 \mapsto t_1$
in the case
$v_1 \mapsto t_1$
in the case
![]() $n = 1$
).
$n = 1$
).
We assume that model theory is set up so that any structure
![]() $\mathcal {M}$
uniquely determines its language, which we denote by
$\mathcal {M}$
uniquely determines its language, which we denote by
![]() $L(\mathcal {M})$
, and we take the symbol “
$L(\mathcal {M})$
, and we take the symbol “
![]() $\mathcal {M}$
” to refer ambiguously to both the structure and its domain. Let
$\mathcal {M}$
” to refer ambiguously to both the structure and its domain. Let
![]() $\mathcal {M}$
be an L-structure,
$\mathcal {M}$
be an L-structure,
![]() $\phi $
a formula in L and
$\phi $
a formula in L and
![]() $f \in \mathrm {VA}^{\mathcal {M}}$
. We use the arrow-notation
$f \in \mathrm {VA}^{\mathcal {M}}$
. We use the arrow-notation
![]() $\vec {a}$
for finite tuples
$\vec {a}$
for finite tuples
![]() $\langle a_1, \ldots , a_n \rangle $
, and the shorthand
$\langle a_1, \ldots , a_n \rangle $
, and the shorthand
![]() $\vec {a} \in \mathcal {M}$
for that each component
$\vec {a} \in \mathcal {M}$
for that each component
![]() $a_i$
of
$a_i$
of
![]() $\vec {a}$
is an element of
$\vec {a}$
is an element of
![]() $\mathcal {M}$
. We write
$\mathcal {M}$
. We write
![]() $\mathcal {M} \models (\phi , f)$
for the statement “
$\mathcal {M} \models (\phi , f)$
for the statement “
![]() $\phi $
is true in
$\phi $
is true in
![]() $\mathcal {M}$
under the variable-assignment f,” as defined in the usual Tarskian semantics of first-order logic. If
$\mathcal {M}$
under the variable-assignment f,” as defined in the usual Tarskian semantics of first-order logic. If
![]() $\vec {a} \in \mathcal {M}$
and
$\vec {a} \in \mathcal {M}$
and
![]() $\psi (\vec {x}) \in L$
, then we write
$\psi (\vec {x}) \in L$
, then we write
![]() $\mathcal {M} \models \psi (\vec {a})$
for
$\mathcal {M} \models \psi (\vec {a})$
for
![]() $\mathcal {M} \models (\psi , \vec {x} \mapsto \vec {a})$
. We write
$\mathcal {M} \models (\psi , \vec {x} \mapsto \vec {a})$
. We write
![]() $\mathcal {M} \models \phi $
for
$\mathcal {M} \models \phi $
for
![]() $\forall f \in \mathrm {VA}^{\mathcal {M}} \hspace {2pt} \mathcal {M} \models (\phi , f)$
. If K is a sublanguage of L, then
$\forall f \in \mathrm {VA}^{\mathcal {M}} \hspace {2pt} \mathcal {M} \models (\phi , f)$
. If K is a sublanguage of L, then
![]() $\mathcal {M}\hspace {-4pt}\restriction _K$
denotes the reduct of
$\mathcal {M}\hspace {-4pt}\restriction _K$
denotes the reduct of
![]() $\mathcal {M}$
to K. We write
$\mathcal {M}$
to K. We write
![]() $\mathcal {M} \equiv _K \mathcal {N}$
for the statement that
$\mathcal {M} \equiv _K \mathcal {N}$
for the statement that
![]() $\mathcal {M}$
satisfy the same K-sentences as
$\mathcal {M}$
satisfy the same K-sentences as
![]() $\mathcal {N}$
. We write
$\mathcal {N}$
. We write
![]() $\mathcal {M} \cong _K \mathcal {N}$
for the statement that
$\mathcal {M} \cong _K \mathcal {N}$
for the statement that
![]() $\mathcal {M}\hspace {-4pt}\restriction _K$
is isomorphic to
$\mathcal {M}\hspace {-4pt}\restriction _K$
is isomorphic to
![]() $\mathcal {N}\hspace {-4pt}\restriction _K$
. When the subscripts are dropped, they are assumed to be
$\mathcal {N}\hspace {-4pt}\restriction _K$
. When the subscripts are dropped, they are assumed to be
![]() $L(\mathcal {M})$
.
$L(\mathcal {M})$
.
We use abbreviations for certain variations of the quantifiers:
-
1.
 $\exists x \in y \hspace {2pt} \phi $
stands for
$\exists x \in y \hspace {2pt} \phi $
stands for
 $\exists x \hspace {2pt} (x \in y \wedge \phi )$
.
$\exists x \hspace {2pt} (x \in y \wedge \phi )$
. -
2.
 $\forall x \in y \hspace {2pt} \phi $
stands for
$\forall x \in y \hspace {2pt} \phi $
stands for
 $\forall x \hspace {2pt} (x \in y \rightarrow \phi )$
.
$\forall x \hspace {2pt} (x \in y \rightarrow \phi )$
. -
3.
 $\exists ^! x \hspace {2pt} \phi $
stands for
$\exists ^! x \hspace {2pt} \phi $
stands for
 $\exists x \hspace {2pt} (\phi (x) \wedge \forall y \hspace {2pt} (\phi (y) \rightarrow x = y))$
.
$\exists x \hspace {2pt} (\phi (x) \wedge \forall y \hspace {2pt} (\phi (y) \rightarrow x = y))$
.
If P is a predicate symbol, we may write
![]() $x \in P$
for
$x \in P$
for
![]() $P(x)$
. Similarly, we write
$P(x)$
. Similarly, we write
![]() $\exists x \in P \hspace {2pt} \phi $
for
$\exists x \in P \hspace {2pt} \phi $
for
![]() $\exists x \hspace {2pt} (P(x) \wedge \phi )$
, and so on.
$\exists x \hspace {2pt} (P(x) \wedge \phi )$
, and so on.
We will introduce primitive relation symbols “
![]() $\mathsf {Sat}$
,” “
$\mathsf {Sat}$
,” “
![]() $\mathsf {Uni}$
” and “
$\mathsf {Uni}$
” and “
![]() $\mathsf {Mod}$
.” Informally,
$\mathsf {Mod}$
.” Informally,
![]() $\mathsf {Sat}(\phi , f)$
expresses that
$\mathsf {Sat}(\phi , f)$
expresses that
![]() $\phi $
is satisfied under the variable assignment f;
$\phi $
is satisfied under the variable assignment f;
![]() $\mathsf {Uni}(\mathcal {U})$
expresses that
$\mathsf {Uni}(\mathcal {U})$
expresses that
![]() $\mathcal {U}$
is a universe; and
$\mathcal {U}$
is a universe; and
![]() $\mathsf {Mod}(\mathcal {U}, \phi , f)$
expresses that
$\mathsf {Mod}(\mathcal {U}, \phi , f)$
expresses that
![]() $\phi $
is satisfied in the universe
$\phi $
is satisfied in the universe
![]() $\mathcal {U}$
under the variable assignment f. Recall that
$\mathcal {U}$
under the variable assignment f. Recall that
![]() $\mathcal {L}_{\mathsf {Sat}}$
denotes the language
$\mathcal {L}_{\mathsf {Sat}}$
denotes the language
![]() $\mathcal {L}$
augmented with the symbol
$\mathcal {L}$
augmented with the symbol
![]() $\mathsf {Sat}$
, while
$\mathsf {Sat}$
, while
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
denotes
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
denotes
![]() $\mathcal {L}$
augmented with
$\mathcal {L}$
augmented with
![]() $\mathsf {Mod}$
and
$\mathsf {Mod}$
and
![]() $\mathsf {Uni}$
.
$\mathsf {Uni}$
.
Again, we introduce some abbreviations:
-
1.
 $\mathsf {Sat}(\phi )$
and
$\mathsf {Sat}(\phi )$
and
 $\mathsf {Tr}(\phi )$
stand for
$\mathsf {Tr}(\phi )$
stand for
 $\forall f \in \mathrm {VA} \hspace {2pt} \mathsf {Sat}(\phi , f)$
.
$\forall f \in \mathrm {VA} \hspace {2pt} \mathsf {Sat}(\phi , f)$
. -
2.
 $\mathsf {Mod}(\mathcal {U}, \phi )$
stands for
$\mathsf {Mod}(\mathcal {U}, \phi )$
stands for
 $\forall f \in \mathrm {VA}^{\mathcal {U}} \hspace {2pt} \mathsf {Mod}(\mathcal {U}, \phi , f)$
.
$\forall f \in \mathrm {VA}^{\mathcal {U}} \hspace {2pt} \mathsf {Mod}(\mathcal {U}, \phi , f)$
. -
3.
 $\mathsf {Tr}^\Box (\phi )$
stands for
$\mathsf {Tr}^\Box (\phi )$
stands for
 $\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} \forall f \in \mathrm {VA}^{\mathcal {U}} \hspace {2pt} \mathsf {Mod}(\mathcal {U}, \phi , f)$
.
$\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} \forall f \in \mathrm {VA}^{\mathcal {U}} \hspace {2pt} \mathsf {Mod}(\mathcal {U}, \phi , f)$
. -
4.
 $\mathsf {Tr}^\Diamond (\phi )$
stands for
$\mathsf {Tr}^\Diamond (\phi )$
stands for
 $\neg \mathsf {Tr}^\Box (\dot \neg \phi )$
.
$\neg \mathsf {Tr}^\Box (\dot \neg \phi )$
.
If X is a formula, term or definable object in the language L of the structure
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $X^{\mathcal {M}}$
denotes its interpretation in
$X^{\mathcal {M}}$
denotes its interpretation in
![]() $\mathcal {M}$
; e.g.,
$\mathcal {M}$
; e.g.,
![]() $\phi ^{\mathcal {M}} =_{\mathrm {df}} \{\vec {a} \in \mathcal {M} \mid \mathcal {M} \models \phi (\vec {a})\}$
.
$\phi ^{\mathcal {M}} =_{\mathrm {df}} \{\vec {a} \in \mathcal {M} \mid \mathcal {M} \models \phi (\vec {a})\}$
.
Informally speaking, if
![]() $\mathcal {M}$
is a model of set theory,
$\mathcal {M}$
is a model of set theory,
![]() $\mathcal {N} \in \mathcal {M}$
, and
$\mathcal {N} \in \mathcal {M}$
, and
![]() $\mathcal {M} \models $
“
$\mathcal {M} \models $
“
![]() $\mathcal {N}$
is a model of set theory,” so that
$\mathcal {N}$
is a model of set theory,” so that
![]() $\mathcal {N}$
is an internal model of
$\mathcal {N}$
is an internal model of
![]() $\mathcal {M}$
, then we may need to extract
$\mathcal {M}$
, then we may need to extract
![]() $\mathcal {N}$
into an external model that can be studied on a par with
$\mathcal {N}$
into an external model that can be studied on a par with
![]() $\mathcal {M}$
. This is achieved by the following formal definition.
$\mathcal {M}$
. This is achieved by the following formal definition.
Definition 2.1. If
![]() $\mathcal {M}$
is a model of set theory and
$\mathcal {M}$
is a model of set theory and
![]() $a \in \mathcal {M}$
, then
$a \in \mathcal {M}$
, then
This notation is generalized in the cases that a is considered as a relation or as a structure: If
![]() $\mathcal {M}$
is a model of set theory,
$\mathcal {M}$
is a model of set theory,
![]() $R \in \mathcal {M}$
and
$R \in \mathcal {M}$
and
![]() $\mathcal {M}$
satisfies that R is an
$\mathcal {M}$
satisfies that R is an
![]() $\underline {n}$
-ary relation (for a natural number n under consideration), then
$\underline {n}$
-ary relation (for a natural number n under consideration), then
 $$ \begin{align*} R_{\mathcal{M}} =_{\mathrm{df}} \big\{ \langle x_1, \ldots, x_n \rangle \mid \hspace{2pt} & \exists p \in \mathcal{M} \hspace{2pt} [ \mathcal{M} \models p \in R \hspace{2pt} \wedge \\ & \bigwedge_{1 \leq i \leq n} \text{“}x_i \text{ is the }\underline{i}\text{:th component of }p”]\big\}. \end{align*} $$
$$ \begin{align*} R_{\mathcal{M}} =_{\mathrm{df}} \big\{ \langle x_1, \ldots, x_n \rangle \mid \hspace{2pt} & \exists p \in \mathcal{M} \hspace{2pt} [ \mathcal{M} \models p \in R \hspace{2pt} \wedge \\ & \bigwedge_{1 \leq i \leq n} \text{“}x_i \text{ is the }\underline{i}\text{:th component of }p”]\big\}. \end{align*} $$
If
![]() $\mathcal {M}$
is a model of set theory,
$\mathcal {M}$
is a model of set theory,
![]() $\mathcal {N}, N, R_1, \ldots , R_n$
are elements of
$\mathcal {N}, N, R_1, \ldots , R_n$
are elements of
![]() $\mathcal {M}$
, and
$\mathcal {M}$
, and
![]() $\mathcal {M}$
satisfies that
$\mathcal {M}$
satisfies that
![]() $\mathcal {N}$
is a structure with domain N and relations
$\mathcal {N}$
is a structure with domain N and relations
![]() $R_1, \ldots , R_n$
(of arities
$R_1, \ldots , R_n$
(of arities
![]() $\underline {r_1}, \ldots , \underline {r_n}$
, respectively), then
$\underline {r_1}, \ldots , \underline {r_n}$
, respectively), then
In either of the above cases
![]() $a_{\mathcal {M}}$
is called the
$a_{\mathcal {M}}$
is called the
![]() $\mathcal {M}$
-externalization of a.
$\mathcal {M}$
-externalization of a.
For example,
![]() $\omega ^{\mathcal {M}}$
denotes the element of
$\omega ^{\mathcal {M}}$
denotes the element of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathcal {M} \models \phi (\omega )$
, where
$\mathcal {M} \models \phi (\omega )$
, where
![]() $\phi $
defines
$\phi $
defines
![]() $\omega $
. On the other hand,
$\omega $
. On the other hand,
![]() $(\omega ^{\mathcal {M}})_{\mathcal {M}}$
denotes the subset
$(\omega ^{\mathcal {M}})_{\mathcal {M}}$
denotes the subset
![]() $\{a \in \mathcal {M} \mid \mathcal {M} \models a \in \omega \}$
of
$\{a \in \mathcal {M} \mid \mathcal {M} \models a \in \omega \}$
of
![]() $\mathcal {M}$
, consisting of all a such that
$\mathcal {M}$
, consisting of all a such that
![]() $\mathcal {M} \models a \in \omega $
.
$\mathcal {M} \models a \in \omega $
.
2.3 Recursive saturation
A type
![]() $p(\vec {x})$
, over a theory T in a language L, is a set of L-formulas such that
$p(\vec {x})$
, over a theory T in a language L, is a set of L-formulas such that
![]() $T \cup p$
is consistent when the variables
$T \cup p$
is consistent when the variables
![]() $\vec {x}$
are considered as fresh constant symbols. If
$\vec {x}$
are considered as fresh constant symbols. If
![]() $\mathcal {M} \models T$
, then
$\mathcal {M} \models T$
, then
![]() $p(\vec {x})$
is realized in
$p(\vec {x})$
is realized in
![]() $\mathcal {M}$
if there is
$\mathcal {M}$
if there is
![]() $\vec {a} \in \mathcal {M}$
, such that for all
$\vec {a} \in \mathcal {M}$
, such that for all
![]() $\phi (\vec {x}) \in p$
, we have
$\phi (\vec {x}) \in p$
, we have
![]() $\mathcal {M} \models \phi (\vec {a})$
. A type
$\mathcal {M} \models \phi (\vec {a})$
. A type
![]() $p(\vec {x}, \vec {b})$
, over
$p(\vec {x}, \vec {b})$
, over
![]() $\mathcal {M}$
with parameters
$\mathcal {M}$
with parameters
![]() $\vec {b} \in \mathcal {M}$
, is a type over
$\vec {b} \in \mathcal {M}$
, is a type over
![]() $\mathrm {Th}(\mathcal {M}, \vec {b})$
(the theory of
$\mathrm {Th}(\mathcal {M}, \vec {b})$
(the theory of
![]() $\mathcal {M}$
with parameters
$\mathcal {M}$
with parameters
![]() $\vec {b}$
). Such a type
$\vec {b}$
). Such a type
![]() $p(\vec {x}, \vec {b})$
is recursive if it is a recursive set (under some fixed Gödel coding of the formulas as natural numbers). A structure
$p(\vec {x}, \vec {b})$
is recursive if it is a recursive set (under some fixed Gödel coding of the formulas as natural numbers). A structure
![]() $\mathcal {M}$
is recursively saturated if it realizes every recursive type over
$\mathcal {M}$
is recursively saturated if it realizes every recursive type over
![]() $\mathcal {M}$
. A
$\mathcal {M}$
. A
![]() $\text {crsm}$
is a countable recursively saturated model.
$\text {crsm}$
is a countable recursively saturated model.
Theorem 2.2 (Completeness of the
 $\text {crsm}$
-semantics)
$\text {crsm}$
-semantics)
Let
![]() $\mathcal {M}$
be a countable model in a recursive language. There is a countable recursively saturated elementary extension of
$\mathcal {M}$
be a countable model in a recursive language. There is a countable recursively saturated elementary extension of
![]() $\mathcal {M}$
. In particular, every consistent theory in a recursive language is modeled by a
$\mathcal {M}$
. In particular, every consistent theory in a recursive language is modeled by a
![]() $\text {crsm}$
.
$\text {crsm}$
.
Proof. See the proof of Theorem 2.4.1 in [Reference Chang and Keisler2].□
Let
![]() $\mathcal {M}$
be a model of a set theory T. The interpretations of the numerals in
$\mathcal {M}$
be a model of a set theory T. The interpretations of the numerals in
![]() $\mathcal {M}$
are called the standard natural numbers of
$\mathcal {M}$
are called the standard natural numbers of
![]() $\mathcal {M}$
. For each
$\mathcal {M}$
. For each
![]() $n < \omega $
, let us make the identification
$n < \omega $
, let us make the identification
![]() $n = \underline {n}^{\mathcal {M}}$
. We say that
$n = \underline {n}^{\mathcal {M}}$
. We say that
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\omega $
-non-standard if there is
$\omega $
-non-standard if there is
![]() $c \in (\omega ^{\mathcal {M}})_{\mathcal {M}} \setminus \omega $
. Such a c is said to be a non-standard number of
$c \in (\omega ^{\mathcal {M}})_{\mathcal {M}} \setminus \omega $
. Such a c is said to be a non-standard number of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proposition 2.3. If
![]() $\mathcal {M}$
is a recursively saturated model of a set theory, then
$\mathcal {M}$
is a recursively saturated model of a set theory, then
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\omega $
-non-standard.
$\omega $
-non-standard.
Proof. By recursive saturation,
![]() $\mathcal {M}$
realizes the type
$\mathcal {M}$
realizes the type
![]() $\{x \in \mathbb {N}\} \cup \{\underline {n} < x \mid n \in \mathbb {N}\}$
.□
$\{x \in \mathbb {N}\} \cup \{\underline {n} < x \mid n \in \mathbb {N}\}$
.□
Suppose that
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\omega $
-non-standard. We say that a subset A of
$\omega $
-non-standard. We say that a subset A of
![]() $\omega $
is coded in
$\omega $
is coded in
![]() $\mathcal {M}$
, if there is (a code)
$\mathcal {M}$
, if there is (a code)
![]() $a \in (\omega ^{\mathcal {M}})_{\mathcal {M}}$
, such that
$a \in (\omega ^{\mathcal {M}})_{\mathcal {M}}$
, such that
![]() $A = \{n \in \mathbb {N} \mid \mathcal {M} \models \underline {n} < a\}$
. We define the standard system of
$A = \{n \in \mathbb {N} \mid \mathcal {M} \models \underline {n} < a\}$
. We define the standard system of
![]() $\mathcal {M}$
as
$\mathcal {M}$
as
The following result is due to [Reference Wilmers17], employing Friedman’s back-and-forth technique [Reference Friedman, Mathias and Rogers4]:
Theorem 2.4 (Canonicity of countable recursively saturated models). Let
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
be
$\mathcal {N}$
be
![]() $\text {crsm}$
s modeling
$\text {crsm}$
s modeling
![]() $\mathsf {ZF}$
. If
$\mathsf {ZF}$
. If
![]() $\mathcal {M} \equiv _{\mathcal {L}} \mathcal {N}$
and
$\mathcal {M} \equiv _{\mathcal {L}} \mathcal {N}$
and
![]() $\mathrm {SSy}(\mathcal {M}) = \mathrm {SSy}(\mathcal {N})$
, then
$\mathrm {SSy}(\mathcal {M}) = \mathrm {SSy}(\mathcal {N})$
, then
![]() $\mathcal {M} \cong _{\mathcal {L}} \mathcal {N}$
.
$\mathcal {M} \cong _{\mathcal {L}} \mathcal {N}$
.
Proof. See the proof of Theorem 7.14 in [Reference Gorbow8].□
Remark. As far as the authors can see, the proof of the above theorem requires both the full Separation and Replacement schemas of
![]() $\mathsf {ZF}$
, as well as its Foundation axiom.
$\mathsf {ZF}$
, as well as its Foundation axiom.
We define the class
2.4 Systems of satisfaction over
 $\mathsf {ZF}$
$\mathsf {ZF}$
Before embarking on developing a framework for a notion of truth-in-a-universe relevant to the set-theoretic multiverse, we shall go through some related systems of truth over
![]() $\mathsf {ZF}$
. An intuitive philosophical perspective is that systems of truth capture various absolute notions of truth, as motivated by the universe view of set theory, while our framework for truth-in-a-universe captures various relative notions of truth, as motivated by the multiverse view of set theory. From a mathematical perspective, it is interesting to relate these two approaches. Moreover, since we will generalize techniques that have been developed for studying systems of truth, these provide a relevant context for viewing our results.
$\mathsf {ZF}$
. An intuitive philosophical perspective is that systems of truth capture various absolute notions of truth, as motivated by the universe view of set theory, while our framework for truth-in-a-universe captures various relative notions of truth, as motivated by the multiverse view of set theory. From a mathematical perspective, it is interesting to relate these two approaches. Moreover, since we will generalize techniques that have been developed for studying systems of truth, these provide a relevant context for viewing our results.
Right at the start of the endeavour to axiomatize truth, one faces the choice between introducing (to the base language of set theory) a unary truth-predicate
![]() $\mathsf {Tr}(\sigma )$
, applying to sentences
$\mathsf {Tr}(\sigma )$
, applying to sentences
![]() $\sigma $
, or a binary satisfaction-relation
$\sigma $
, or a binary satisfaction-relation
![]() $\mathsf {Sat}(\phi , f)$
, applying to formulas
$\mathsf {Sat}(\phi , f)$
, applying to formulas
![]() $\phi $
and variable-assignments
$\phi $
and variable-assignments
![]() $f : \mathrm {Var} \rightarrow V$
. In the former option,
$f : \mathrm {Var} \rightarrow V$
. In the former option,
![]() $\sigma $
needs to range over a class-sized language where there is a constant-symbol
$\sigma $
needs to range over a class-sized language where there is a constant-symbol
![]() $c_x$
corresponding to each
$c_x$
corresponding to each
![]() $x \in V$
. The authors have chosen the latter option. As a general heuristic, one is justified to expect any theory of satisfaction to be interpretable in a corresponding theory of truth; the idea being to interpret
$x \in V$
. The authors have chosen the latter option. As a general heuristic, one is justified to expect any theory of satisfaction to be interpretable in a corresponding theory of truth; the idea being to interpret
![]() $\mathsf {Sat}(\phi (x), f)$
by
$\mathsf {Sat}(\phi (x), f)$
by
![]() $\mathsf {Tr}(\phi [c_{f(x)}/x])$
. Fujimoto has made a comprehensive study of theories of truth over set theory, following the former option [Reference Fujimoto6].
$\mathsf {Tr}(\phi [c_{f(x)}/x])$
. Fujimoto has made a comprehensive study of theories of truth over set theory, following the former option [Reference Fujimoto6].
System 2.5 (
 $\mathsf {CT}$
)
$\mathsf {CT}$
)
Let S be a set theory in
![]() $\mathcal {L}^+$
. The system
$\mathcal {L}^+$
. The system
![]() $\mathsf {CT}(S)\hspace {-4pt}\restriction $
(for Compositional Truth) consists of these axioms in the language
$\mathsf {CT}(S)\hspace {-4pt}\restriction $
(for Compositional Truth) consists of these axioms in the language
![]() $\mathcal {L}^+_{\mathsf {Sat}}$
:
$\mathcal {L}^+_{\mathsf {Sat}}$
:
 $$ \begin{align*} \begin{array}{ll} \mathsf{Base} & S, \\ \mathsf{CT}_= & \forall y_0, y_1 \hspace{2pt} \big( \mathsf{Sat}(\ulcorner x_0 = x_1 \urcorner, \langle \ulcorner x_0 \urcorner, \ulcorner x_1 \urcorner \rangle \mapsto \langle y_0, y_1 \rangle) \leftrightarrow y_0 = y_1 \big), \\ \mathsf{CT}_\in & \forall y_0, y_1 \hspace{2pt} \big( \mathsf{Sat}(\ulcorner x_0 \in x_1 \urcorner, \langle \ulcorner x_0 \urcorner, \ulcorner x_1 \urcorner \rangle \mapsto \langle y_0, y_1 \rangle) \leftrightarrow y_0 \in y_1 \big), \\ \mathsf{CT}_\neg & \forall \phi \in \mathcal{L}^+_{\mathsf{Sat}} \hspace{2pt} \forall f \in \mathrm{VA} \hspace{2pt} (\mathsf{Sat}(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\neg} \phi, f) \leftrightarrow \neg \mathsf{Sat}(\phi, f)), \\ \mathsf{CT}_\wedge & \forall \phi, \psi \in \mathcal{L}^+_{\mathsf{Sat}} \hspace{2pt} \forall f \in \mathrm{VA} \hspace{2pt} (\mathsf{Sat}(\phi \mathrel{\underset{\substack{\\[-9.5pt]\mbox{.}}}{\wedge}} \psi, f) \leftrightarrow \mathsf{Sat}(\phi, f) \wedge \mathsf{Sat}(\psi, f)), \\ \mathsf{CT}_\forall & \forall \phi \in \mathcal{L}^+_{\mathsf{Sat}} \hspace{2pt} \forall f \in \mathrm{VA} \hspace{2pt} (\mathsf{Sat}(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\forall} u \hspace{2pt} \phi, f) \leftrightarrow \forall g \in \mathrm{VA}_{f, u} \hspace{2pt} \mathsf{Sat}(\phi, g)). \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathsf{Base} & S, \\ \mathsf{CT}_= & \forall y_0, y_1 \hspace{2pt} \big( \mathsf{Sat}(\ulcorner x_0 = x_1 \urcorner, \langle \ulcorner x_0 \urcorner, \ulcorner x_1 \urcorner \rangle \mapsto \langle y_0, y_1 \rangle) \leftrightarrow y_0 = y_1 \big), \\ \mathsf{CT}_\in & \forall y_0, y_1 \hspace{2pt} \big( \mathsf{Sat}(\ulcorner x_0 \in x_1 \urcorner, \langle \ulcorner x_0 \urcorner, \ulcorner x_1 \urcorner \rangle \mapsto \langle y_0, y_1 \rangle) \leftrightarrow y_0 \in y_1 \big), \\ \mathsf{CT}_\neg & \forall \phi \in \mathcal{L}^+_{\mathsf{Sat}} \hspace{2pt} \forall f \in \mathrm{VA} \hspace{2pt} (\mathsf{Sat}(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\neg} \phi, f) \leftrightarrow \neg \mathsf{Sat}(\phi, f)), \\ \mathsf{CT}_\wedge & \forall \phi, \psi \in \mathcal{L}^+_{\mathsf{Sat}} \hspace{2pt} \forall f \in \mathrm{VA} \hspace{2pt} (\mathsf{Sat}(\phi \mathrel{\underset{\substack{\\[-9.5pt]\mbox{.}}}{\wedge}} \psi, f) \leftrightarrow \mathsf{Sat}(\phi, f) \wedge \mathsf{Sat}(\psi, f)), \\ \mathsf{CT}_\forall & \forall \phi \in \mathcal{L}^+_{\mathsf{Sat}} \hspace{2pt} \forall f \in \mathrm{VA} \hspace{2pt} (\mathsf{Sat}(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\forall} u \hspace{2pt} \phi, f) \leftrightarrow \forall g \in \mathrm{VA}_{f, u} \hspace{2pt} \mathsf{Sat}(\phi, g)). \\ \end{array} \end{align*} $$
We write
![]() $\mathsf {CT}\hspace {-4pt}\restriction $
for
$\mathsf {CT}\hspace {-4pt}\restriction $
for
![]() $\mathsf {CT}(\mathsf {ZF})\hspace {-4pt}\restriction $
. The axioms of the form
$\mathsf {CT}(\mathsf {ZF})\hspace {-4pt}\restriction $
. The axioms of the form
![]() $\mathsf {CT}_-$
are called compositional axioms. By basic logic,
$\mathsf {CT}_-$
are called compositional axioms. By basic logic,
![]() $\mathsf {CT}\hspace {-4pt}\restriction $
also proves the axioms
$\mathsf {CT}\hspace {-4pt}\restriction $
also proves the axioms
![]() $\mathsf {CT}_\vee $
,
$\mathsf {CT}_\vee $
,
![]() $\mathsf {CT}^\rightarrow $
and
$\mathsf {CT}^\rightarrow $
and
![]() $\mathsf {CT}_\exists $
(analogously defined). We use phrases such as “
$\mathsf {CT}_\exists $
(analogously defined). We use phrases such as “
![]() $\mathsf {Sat}$
is
$\mathsf {Sat}$
is
![]() $\vee $
-compositional” to express that we have
$\vee $
-compositional” to express that we have
![]() $\mathsf {CT}_\vee $
, for example.
$\mathsf {CT}_\vee $
, for example.
![]() $\mathsf {CT}$
is
$\mathsf {CT}$
is
![]() $\mathsf {CT}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Sat}})$
.
$\mathsf {CT}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Sat}})$
.
A routine induction argument in the meta-theory shows this proposition:
Proposition 2.6. For all
![]() $\mathcal {L}$
-formulas
$\mathcal {L}$
-formulas
![]() $\phi (x)$
,
$\phi (x)$
,
![]() $\mathsf {CT}\hspace {-4pt}\restriction \hspace {3pt} \vdash \mathsf {Sat}(\ulcorner \phi (x) \urcorner , \ulcorner x \urcorner \mapsto y) \leftrightarrow \phi (y)$
.
$\mathsf {CT}\hspace {-4pt}\restriction \hspace {3pt} \vdash \mathsf {Sat}(\ulcorner \phi (x) \urcorner , \ulcorner x \urcorner \mapsto y) \leftrightarrow \phi (y)$
.
The theory of satisfaction
![]() $\mathsf {CT}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
corresponds to the theory of truth
$\mathsf {CT}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
corresponds to the theory of truth
![]() $\mathsf {TC}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}^+$
in [Reference Fujimoto6, sec. Reference Friedman, Mathias and Rogers4]. It is straightforward to interpret the former in the latter. Using this, it follows from Theorem 20 in [Reference Fujimoto6, sec. Reference Friedman, Mathias and Rogers4.Reference Broberg1] that
$\mathsf {TC}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}^+$
in [Reference Fujimoto6, sec. Reference Friedman, Mathias and Rogers4]. It is straightforward to interpret the former in the latter. Using this, it follows from Theorem 20 in [Reference Fujimoto6, sec. Reference Friedman, Mathias and Rogers4.Reference Broberg1] that
![]() $\mathsf {CT}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
is conservative over
$\mathsf {CT}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
is conservative over
![]() $\mathsf {ZF}$
. In contrast, in
$\mathsf {ZF}$
. In contrast, in
![]() $\mathsf {CT}$
we have access to the Reflection theorem for
$\mathsf {CT}$
we have access to the Reflection theorem for
![]() $\mathcal {L}_{\mathsf {Sat}}$
-formulas, enabling us to prove that there is a
$\mathcal {L}_{\mathsf {Sat}}$
-formulas, enabling us to prove that there is a
![]() $V_\alpha $
modeling
$V_\alpha $
modeling
![]() $\mathsf {ZF}$
. See [Reference Fujimoto6, sec. Reference Friedman, Mathias and Rogers4.Reference Broberg1] for more details and refinements.
$\mathsf {ZF}$
. See [Reference Fujimoto6, sec. Reference Friedman, Mathias and Rogers4.Reference Broberg1] for more details and refinements.
Proposition 2.7.
![]() $\mathsf {CT}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}}) \vdash “\text {Transfinite Induction over } \mathcal {L}_{\mathsf {Sat}}\text {.”}$
$\mathsf {CT}\hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}}) \vdash “\text {Transfinite Induction over } \mathcal {L}_{\mathsf {Sat}}\text {.”}$
Proof. Let
![]() $\phi (x) \in \mathcal {L}_{\mathsf {Sat}}$
. Assuming
$\phi (x) \in \mathcal {L}_{\mathsf {Sat}}$
. Assuming
![]() $\neg \phi (\alpha )$
, for some ordinal
$\neg \phi (\alpha )$
, for some ordinal
![]() $\alpha $
, we shall refute the corresponding induction hypothesis. By
$\alpha $
, we shall refute the corresponding induction hypothesis. By
![]() $\mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
, the set
$\mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
, the set
![]() $S = \{\xi \leq \alpha \mid \neg \phi (\xi )\}$
exists, and by assumption it is non-empty. Let
$S = \{\xi \leq \alpha \mid \neg \phi (\xi )\}$
exists, and by assumption it is non-empty. Let
![]() $\beta $
be the least ordinal in S. Then
$\beta $
be the least ordinal in S. Then
![]() $\neg \phi (\beta )$
and
$\neg \phi (\beta )$
and
![]() $\forall \xi < \beta \hspace {2pt} \phi (\xi )$
, refuting the induction hypothesis.□
$\forall \xi < \beta \hspace {2pt} \phi (\xi )$
, refuting the induction hypothesis.□
System 2.8 (
 $\mathsf {GR}^\omega $
)
$\mathsf {GR}^\omega $
)
Let S be a set theory in
![]() $\mathcal {L}^+$
. Here we present the systems of iterated Global Reflection over S, denoted
$\mathcal {L}^+$
. Here we present the systems of iterated Global Reflection over S, denoted
![]() $\mathsf {GR}^\alpha (S)$
, for ordinals
$\mathsf {GR}^\alpha (S)$
, for ordinals
![]() $\alpha \leq \omega $
. For any set theory T in the language
$\alpha \leq \omega $
. For any set theory T in the language
![]() $\mathcal {L}_{\mathsf {Sat}}$
, the axiom of Global Reflection over T is
$\mathcal {L}_{\mathsf {Sat}}$
, the axiom of Global Reflection over T is
(The dot under T is sometimes omitted, when it can be inferred from the context.)
Recursively, for each
![]() $\alpha \leq \omega $
, we define the system
$\alpha \leq \omega $
, we define the system
![]() $\mathsf {GR}^\alpha (S)$
:
$\mathsf {GR}^\alpha (S)$
:
 $$ \begin{align*} \mathsf{GR}^0(S) &=_{\mathrm{df}} \mathsf{CT}(S) \hspace{-4pt}\restriction + \hspace{2pt} \mathsf{Sep}(\mathcal{L}^+_{\mathsf{Sat}}), \\ \mathsf{GR}^{\alpha+1}(S) &=_{\mathrm{df}} \mathsf{GR}^\alpha(S) + \mathsf{GR}_{\mathsf{GR}^{\alpha}}, \\ \mathsf{GR}^\omega(S) &=_{\mathrm{df}} \bigcup_{n < \omega} \mathsf{GR}^n(S). \end{align*} $$
$$ \begin{align*} \mathsf{GR}^0(S) &=_{\mathrm{df}} \mathsf{CT}(S) \hspace{-4pt}\restriction + \hspace{2pt} \mathsf{Sep}(\mathcal{L}^+_{\mathsf{Sat}}), \\ \mathsf{GR}^{\alpha+1}(S) &=_{\mathrm{df}} \mathsf{GR}^\alpha(S) + \mathsf{GR}_{\mathsf{GR}^{\alpha}}, \\ \mathsf{GR}^\omega(S) &=_{\mathrm{df}} \bigcup_{n < \omega} \mathsf{GR}^n(S). \end{align*} $$
We write
![]() $\mathsf {GR}^\alpha $
for
$\mathsf {GR}^\alpha $
for
![]() $\mathsf {GR}^\alpha (\mathsf {ZF})$
.
$\mathsf {GR}^\alpha (\mathsf {ZF})$
.
Remark. Observe that
![]() $\mathsf {GR}^\alpha $
is defined with
$\mathsf {GR}^\alpha $
is defined with
![]() $\mathsf {CT} \hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
as base case, thus without Replacement for formulas with the Satisfaction predicate. The reason for this is that it is intended to express iterated Global Reflection over
$\mathsf {CT} \hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
as base case, thus without Replacement for formulas with the Satisfaction predicate. The reason for this is that it is intended to express iterated Global Reflection over
![]() $\mathsf {ZF}$
, which
$\mathsf {ZF}$
, which
![]() $\mathsf {CT} \hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
conservatively extends. If it were defined with
$\mathsf {CT} \hspace {-4pt}\restriction + \hspace {2pt} \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
conservatively extends. If it were defined with
![]() $\mathsf {CT}$
as base case, then it would not be morally “over
$\mathsf {CT}$
as base case, then it would not be morally “over
![]() $\mathsf {ZF}$
,” since
$\mathsf {ZF}$
,” since
![]() $\mathsf {CT}$
proves strong reflection principles of its own.
$\mathsf {CT}$
proves strong reflection principles of its own.
System 2.9 (
 $\mathsf {FS}$
)
$\mathsf {FS}$
)
The systems
![]() $\mathsf {FS}\hspace {-3pt}\restriction $
and
$\mathsf {FS}\hspace {-3pt}\restriction $
and
![]() $\mathsf {FS}$
(for Friedman–Sheard) are obtained by adding these rules of proof to
$\mathsf {FS}$
(for Friedman–Sheard) are obtained by adding these rules of proof to
![]() $\mathsf {CT}\hspace {-3pt}\restriction $
and
$\mathsf {CT}\hspace {-3pt}\restriction $
and
![]() $\mathsf {CT}$
, respectively:
$\mathsf {CT}$
, respectively:
Recall that
![]() $\mathsf {Tr}(\theta )$
is defined as
$\mathsf {Tr}(\theta )$
is defined as
![]() $\forall f \in \mathrm {VA} \hspace {2pt} \mathsf {Sat}(\theta , f)$
.
$\forall f \in \mathrm {VA} \hspace {2pt} \mathsf {Sat}(\theta , f)$
.
Given a set-theoretic system S in language L, the following rule will be considered:
Definition 2.10. A set-theoretic system S in language L is
![]() $\omega $
-inconsistent if there is an L-formula
$\omega $
-inconsistent if there is an L-formula
such that:

We say that
witnesses the
![]() $\omega $
-inconsistency of S.Footnote
7
$\omega $
-inconsistency of S.Footnote
7
Proposition 2.11. If
![]() $\, \mathsf {ZF}$
is
$\, \mathsf {ZF}$
is
![]() $\omega $
-consistent, then
$\omega $
-consistent, then
![]() $\mathsf {ZF}$
is closed under the Reflection rule.
$\mathsf {ZF}$
is closed under the Reflection rule.
Proof. Suppose
![]() $\mathsf {ZF} \not \vdash \phi $
. Then
$\mathsf {ZF} \not \vdash \phi $
. Then
![]() $\mathsf {ZF} \vdash \neg \Pr _{\mathsf {ZF}}(\underline {n}, \ulcorner \phi \urcorner )$
, for every standard
$\mathsf {ZF} \vdash \neg \Pr _{\mathsf {ZF}}(\underline {n}, \ulcorner \phi \urcorner )$
, for every standard
![]() $n \in \mathbb {N}$
(where
$n \in \mathbb {N}$
(where
![]() $\Pr _{\mathsf {ZF}}(\underline {n}, \ulcorner \phi \urcorner )$
is the formula expressing that
$\Pr _{\mathsf {ZF}}(\underline {n}, \ulcorner \phi \urcorner )$
is the formula expressing that
![]() $\underline {n}$
is the Gödel code of a proof of
$\underline {n}$
is the Gödel code of a proof of
![]() $\phi $
). Now, by
$\phi $
). Now, by
![]() $\omega $
-consistency,
$\omega $
-consistency,
![]() $\mathsf {ZF} \vdash \neg \Pr _{\mathsf {ZF}}(\ulcorner \phi \urcorner )$
.□
$\mathsf {ZF} \vdash \neg \Pr _{\mathsf {ZF}}(\ulcorner \phi \urcorner )$
.□
Let c be a fresh constant symbol. Note that the schema
![]() $\{\underline {m} < c < \omega \mid m \in \mathbb {N}\}$
, expressing that there is a non-standard natural number, yields
$\{\underline {m} < c < \omega \mid m \in \mathbb {N}\}$
, expressing that there is a non-standard natural number, yields
![]() $\omega $
-inconsistency when added to a set-theoretic system (proof: take
$\omega $
-inconsistency when added to a set-theoretic system (proof: take
![]() $x = c$
as
$x = c$
as
![]() ).
).
Proposition 2.12.
![]() $\mathsf {GR}^\omega $
and
$\mathsf {GR}^\omega $
and
![]() $\mathsf {FS}$
are
$\mathsf {FS}$
are
![]() $\omega $
-inconsistent.
$\omega $
-inconsistent.
![]() $\mathsf {GR}^\omega + \mathsf {GR}_{\mathsf {GR}^\omega }$
and
$\mathsf {GR}^\omega + \mathsf {GR}_{\mathsf {GR}^\omega }$
and
![]() $\mathsf {FS} + \mathsf {GR}_{\mathsf {FS}}$
are inconsistent.
$\mathsf {FS} + \mathsf {GR}_{\mathsf {FS}}$
are inconsistent.
Proof. This is a corollary of McGee’s paradox, see [Reference McGee15], and can be proved analogously as Theorem 13.9 and Corollary 14.39 in [Reference Halbach11], respectively. The arguments in [Reference Halbach11] are written for theories of truth over
![]() $\mathsf {PA}$
, not for theories of satisfaction over
$\mathsf {PA}$
, not for theories of satisfaction over
![]() $\mathsf {ZF}$
. But they go through with these natural modifications:
$\mathsf {ZF}$
. But they go through with these natural modifications:
-
1. Replacing instances of the truth predicate “T” by our defined predicate “
 $\mathsf {Tr}$
,” except for instances quantifying over terms, of the form
$\mathsf {Tr}$
,” except for instances quantifying over terms, of the form
 $\forall \vec {t} \hspace {2pt} T(\phi \text {\d {{[}}} \vec {t} \underset {\substack {\\[-9.5pt]\mbox {.}}}{/} \ulcorner \vec {x} \urcorner \text {\d {{]}}})$
, which are replaced by
$\forall \vec {t} \hspace {2pt} T(\phi \text {\d {{[}}} \vec {t} \underset {\substack {\\[-9.5pt]\mbox {.}}}{/} \ulcorner \vec {x} \urcorner \text {\d {{]}}})$
, which are replaced by
 $\forall \vec {y} \in \omega \hspace {2pt} \mathsf {Sat}(\phi , \ulcorner \vec {x} \urcorner \mapsto \vec {y})$
, where
$\forall \vec {y} \in \omega \hspace {2pt} \mathsf {Sat}(\phi , \ulcorner \vec {x} \urcorner \mapsto \vec {y})$
, where
 $\vec {y}$
is fresh.
$\vec {y}$
is fresh. -
2. Replacing quantifiers of the form “
 $\forall x$
” by “
$\forall x$
” by “
 $\forall x \in \omega $
.”
$\forall x \in \omega $
.”
These arguments rely on that
![]() $\mathsf {GR}^\omega $
admits
$\mathsf {GR}^\omega $
admits
![]() $\mathsf {NEC}$
, which we proceed to show: Let
$\mathsf {NEC}$
, which we proceed to show: Let
![]() $\sigma \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}})$
and suppose that
$\sigma \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}})$
and suppose that
![]() $\mathsf {GR}^\omega \vdash \sigma $
. Then there is
$\mathsf {GR}^\omega \vdash \sigma $
. Then there is
![]() $k < \omega $
, such that
$k < \omega $
, such that
![]() $\mathsf {GR}^k \vdash \sigma $
. since this proof can be represented in
$\mathsf {GR}^k \vdash \sigma $
. since this proof can be represented in
![]() $\mathsf {GR}^\omega $
, we have
$\mathsf {GR}^\omega $
, we have
![]() $\mathsf {GR}^\omega \vdash \Pr _{\mathsf {GR}^k}(\ulcorner \sigma \urcorner )$
, so that by Global Reflection,
$\mathsf {GR}^\omega \vdash \Pr _{\mathsf {GR}^k}(\ulcorner \sigma \urcorner )$
, so that by Global Reflection,
![]() $\mathsf {GR}^\omega \vdash \mathsf {Tr}(\ulcorner \sigma \urcorner )$
. Since
$\mathsf {GR}^\omega \vdash \mathsf {Tr}(\ulcorner \sigma \urcorner )$
. Since
![]() $\mathsf {GR}^\omega \vdash \mathsf {CT}\hspace {-4pt}\restriction $
, it follows that
$\mathsf {GR}^\omega \vdash \mathsf {CT}\hspace {-4pt}\restriction $
, it follows that
![]() $\mathsf {GR}^\omega \vdash \sigma $
, as desired.□
$\mathsf {GR}^\omega \vdash \sigma $
, as desired.□
So if we were to naturally extend the definition of
![]() $\mathsf {GR}^\alpha $
to all ordinals
$\mathsf {GR}^\alpha $
to all ordinals
![]() $\alpha $
, then we would get that
$\alpha $
, then we would get that
![]() $\mathsf {GR}^\alpha $
is inconsistent for all
$\mathsf {GR}^\alpha $
is inconsistent for all
![]() $\alpha> \omega $
.
$\alpha> \omega $
.
Later on we will introduce a multiverse axiom, called
![]() $\textsf {Self-Perception}$
, to the effect that the universe of the background theory is isomorphic (over
$\textsf {Self-Perception}$
, to the effect that the universe of the background theory is isomorphic (over
![]() $\mathcal {L}$
) to one of its internal universes; this axiom is motivated by the idea that the universe of the background theory should be available in its multiverse. The following lemmas establish technical results needed to validate that axiom.
$\mathcal {L}$
) to one of its internal universes; this axiom is motivated by the idea that the universe of the background theory should be available in its multiverse. The following lemmas establish technical results needed to validate that axiom.
Lemma 2.13. Let
![]() $\mathcal {U}$
be a
$\mathcal {U}$
be a
![]() $\text {crsm}$
of
$\text {crsm}$
of
![]() $\mathsf {GR}_0$
and let
$\mathsf {GR}_0$
and let
![]() $\mathcal {V} \in \mathcal {U}$
, such that
$\mathcal {V} \in \mathcal {U}$
, such that
![]() $\mathcal {U}$
satisfies
$\mathcal {U}$
satisfies
Then
![]() $\mathcal {U} \cong _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
.
$\mathcal {U} \cong _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
.
Recall that
![]() $\mathcal {V}_{\mathcal {U}}$
is the
$\mathcal {V}_{\mathcal {U}}$
is the
![]() $\mathcal {U}$
-externalization of
$\mathcal {U}$
-externalization of
![]() $\mathcal {V}$
, see Definition 2.1.
$\mathcal {V}$
, see Definition 2.1.
Proof. We shall establish
![]() $\mathcal {U} \cong _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
by invoking Theorem 2.4. Thus we need to show that
$\mathcal {U} \cong _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
by invoking Theorem 2.4. Thus we need to show that
![]() $\mathcal {V}_{\mathcal {U}}$
is a
$\mathcal {V}_{\mathcal {U}}$
is a
![]() $\text {crsm}$
, that
$\text {crsm}$
, that
![]() $\mathrm {SSy}(\mathcal {U}) = \mathrm {SSy}(\mathcal {V}_{\mathcal {U}})$
and that
$\mathrm {SSy}(\mathcal {U}) = \mathrm {SSy}(\mathcal {V}_{\mathcal {U}})$
and that
![]() $\mathcal {U} \equiv _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
.
$\mathcal {U} \equiv _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
.
Note that
![]() $\mathcal {U}$
is
$\mathcal {U}$
is
![]() $\omega $
-non-standard, by
$\omega $
-non-standard, by
![]() $\mathcal {U} \in \mathbf {crsm}$
and Proposition 2.3. That
$\mathcal {U} \in \mathbf {crsm}$
and Proposition 2.3. That
![]() $\mathcal {V}_{\mathcal {U}}$
is a
$\mathcal {V}_{\mathcal {U}}$
is a
![]() $\text {crsm}$
now follows from Lemma 2.2 in [Reference Gitman and Hamkins7].Footnote
8
$\text {crsm}$
now follows from Lemma 2.2 in [Reference Gitman and Hamkins7].Footnote
8
![]() $(\omega ^{\mathcal {U}})_{\mathcal {U}}$
is mapped initially into
$(\omega ^{\mathcal {U}})_{\mathcal {U}}$
is mapped initially into
![]() $(\omega ^{(\mathcal {V}_{\mathcal {U}})})_{(\mathcal {V}_{\mathcal {U}})}$
by an embedding j (for each
$(\omega ^{(\mathcal {V}_{\mathcal {U}})})_{(\mathcal {V}_{\mathcal {U}})}$
by an embedding j (for each
![]() $x \in (\omega ^{\mathcal {U}})_{\mathcal {U}}$
,
$x \in (\omega ^{\mathcal {U}})_{\mathcal {U}}$
,
![]() $j(x)$
is defined as the unique
$j(x)$
is defined as the unique
![]() $y \in \mathcal {U}$
such that
$y \in \mathcal {U}$
such that
![]() $\mathcal {U} \models y = \underline {x}^{\mathcal {V}}$
). Therefore, we obtain
$\mathcal {U} \models y = \underline {x}^{\mathcal {V}}$
). Therefore, we obtain
![]() $\mathrm {SSy}(\mathcal {U}) = \mathrm {SSy}(\mathcal {V}_{\mathcal {U}})$
as follows: Let
$\mathrm {SSy}(\mathcal {U}) = \mathrm {SSy}(\mathcal {V}_{\mathcal {U}})$
as follows: Let
![]() $A \in \mathrm {SSy}(\mathcal {U})$
, coded by
$A \in \mathrm {SSy}(\mathcal {U})$
, coded by
![]() $a \in (\omega ^{\mathcal {U}})_{\mathcal {U}}$
. Since j is an embedding,
$a \in (\omega ^{\mathcal {U}})_{\mathcal {U}}$
. Since j is an embedding,
![]() $j(a)$
is a code for A in
$j(a)$
is a code for A in
![]() $(\omega ^{(\mathcal {V}_{\mathcal {U}})})_{(\mathcal {V}_{\mathcal {U}})}$
. Conversely, let
$(\omega ^{(\mathcal {V}_{\mathcal {U}})})_{(\mathcal {V}_{\mathcal {U}})}$
. Conversely, let
![]() $B \in \mathrm {SSy}(\mathcal {V}_{\mathcal {U}})$
, coded by
$B \in \mathrm {SSy}(\mathcal {V}_{\mathcal {U}})$
, coded by
![]() $b \in (\omega ^{(\mathcal {V}_{\mathcal {U}})})_{(\mathcal {V}_{\mathcal {U}})}$
. Since j is initial and
$b \in (\omega ^{(\mathcal {V}_{\mathcal {U}})})_{(\mathcal {V}_{\mathcal {U}})}$
. Since j is initial and
![]() $\mathcal {U}$
is
$\mathcal {U}$
is
![]() $\omega $
-non-standard, there is a non-standard
$\omega $
-non-standard, there is a non-standard
![]() $c \in (\omega ^{\mathcal {U}})_{\mathcal {U}}$
, such that
$c \in (\omega ^{\mathcal {U}})_{\mathcal {U}}$
, such that
![]() $j(c) \leq ^{\mathcal {V}_{\mathcal {U}}} b$
. So since j is an embedding, c is a code for B in
$j(c) \leq ^{\mathcal {V}_{\mathcal {U}}} b$
. So since j is an embedding, c is a code for B in
![]() $(\omega ^{\mathcal {U}})_{\mathcal {U}}$
.
$(\omega ^{\mathcal {U}})_{\mathcal {U}}$
.
To see
![]() $\mathcal {U} \equiv _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
, let
$\mathcal {U} \equiv _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
, let
![]() $\phi $
be a sentence of
$\phi $
be a sentence of
![]() $\mathcal {L}$
. By absoluteness of
$\mathcal {L}$
. By absoluteness of
![]() $\models $
for standard formulas,
$\models $
for standard formulas,
Since
![]() $\mathsf {Sat}$
satisfies the Tarski-biconditionals for
$\mathsf {Sat}$
satisfies the Tarski-biconditionals for
![]() $\mathcal {L}$
, we have
$\mathcal {L}$
, we have
Moreover, by
![]() $\mathsf {CT}_\neg $
and the condition of the lemma,
$\mathsf {CT}_\neg $
and the condition of the lemma,
By combining these we obtain
![]() $\mathcal {U} \equiv _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
, as desired.□
$\mathcal {U} \equiv _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
, as desired.□
Remark.
![]() $\mathcal {U} \models \mathsf {ZF}$
is needed for the proof of this lemma, as it relies on Theorem 2.4. Thus, the authors do not expect it to generalize to
$\mathcal {U} \models \mathsf {ZF}$
is needed for the proof of this lemma, as it relies on Theorem 2.4. Thus, the authors do not expect it to generalize to
![]() $\mathsf {GR}_0(S)$
, unless
$\mathsf {GR}_0(S)$
, unless
![]() $S \vdash \mathsf {ZF}$
.
$S \vdash \mathsf {ZF}$
.
Lemma 2.14. Let
![]() $k < \alpha \leq \omega $
, and let
$k < \alpha \leq \omega $
, and let
![]() $\mathcal {U} \models \mathsf {GR}^\alpha $
. Then there is
$\mathcal {U} \models \mathsf {GR}^\alpha $
. Then there is
![]() $\mathcal {V} \in \mathcal {U}$
, such that
$\mathcal {V} \in \mathcal {U}$
, such that
![]() $\mathcal {U}$
satisfies
$\mathcal {U}$
satisfies
In particular,
![]() $\mathcal {U}$
satisfies that
$\mathcal {U}$
satisfies that
![]() $\mathcal {V} \models \mathsf {GR}^k$
. Moreover, if
$\mathcal {V} \models \mathsf {GR}^k$
. Moreover, if
![]() $\mathcal {U} \in \mathbf {crsm}$
, then
$\mathcal {U} \in \mathbf {crsm}$
, then
![]() $\mathcal {U} \cong _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
.
$\mathcal {U} \cong _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
.
Proof. We work in
![]() $\mathcal {U}$
. From
$\mathcal {U}$
. From
![]() $\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
we get that the set
$\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
we get that the set
![]() $\mathbf {Tr} = \{\phi \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\phi )\}$
exists. For the first statement, by completeness of the
$\mathbf {Tr} = \{\phi \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\phi )\}$
exists. For the first statement, by completeness of the
![]() $\text {crsm}$
-semantics (Theorem 2.2), it suffices to establish
$\text {crsm}$
-semantics (Theorem 2.2), it suffices to establish
![]() $\mathrm {Con}(\mathbf {Tr})$
; and for this it suffices to establish
$\mathrm {Con}(\mathbf {Tr})$
; and for this it suffices to establish
![]() $\mathrm {Con}(\sigma )$
, where
$\mathrm {Con}(\sigma )$
, where
![]() $\sigma $
is an arbitrary finite conjunction of sentences in
$\sigma $
is an arbitrary finite conjunction of sentences in
![]() $\mathbf {Tr}$
. By
$\mathbf {Tr}$
. By
![]() $\wedge $
-compositionality of
$\wedge $
-compositionality of
![]() $\mathsf {Sat}$
, we have
$\mathsf {Sat}$
, we have
![]() $\mathsf {Sat}(\sigma )$
. By
$\mathsf {Sat}(\sigma )$
. By
![]() $\mathsf {GR}_{\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})}$
, we have
$\mathsf {GR}_{\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})}$
, we have
![]() $\mathrm {Pr}_{\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma ) \rightarrow \mathsf {Sat}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma )$
, and by
$\mathrm {Pr}_{\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma ) \rightarrow \mathsf {Sat}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma )$
, and by
![]() $\neg $
-compositionality of
$\neg $
-compositionality of
![]() $\mathsf {Sat}$
, we have
$\mathsf {Sat}$
, we have
![]() $\mathsf {Sat}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma ) \leftrightarrow \neg \mathsf {Sat}(\sigma )$
. So since
$\mathsf {Sat}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma ) \leftrightarrow \neg \mathsf {Sat}(\sigma )$
. So since
![]() $\mathsf {Sat}(\sigma )$
, we obtain
$\mathsf {Sat}(\sigma )$
, we obtain
![]() $\mathrm {Pr}_{\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma ) \rightarrow \bot $
, whence
$\mathrm {Pr}_{\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma ) \rightarrow \bot $
, whence
![]() $\mathrm {Con}(\sigma )$
. By Theorem 2.2, we can let
$\mathrm {Con}(\sigma )$
. By Theorem 2.2, we can let
![]() $\mathcal {V}$
be a model of
$\mathcal {V}$
be a model of
![]() $\mathbf {Tr}$
in
$\mathbf {Tr}$
in
![]() $\mathbf {crsm}$
.
$\mathbf {crsm}$
.
It follows from
![]() $\mathsf {GR}_{\mathsf {GR}^k}$
that
$\mathsf {GR}_{\mathsf {GR}^k}$
that
![]() $\mathsf {GR}^k \subseteq \mathbf {Tr}$
, yielding the second statement.
$\mathsf {GR}^k \subseteq \mathbf {Tr}$
, yielding the second statement.
The last statement now follows from Lemma 2.13.□
Axiom 2.15. Let
![]() $\iota $
be a function symbol and
$\iota $
be a function symbol and
![]() $\mathsf {self}$
be a constant symbol.
$\mathsf {self}$
be a constant symbol.
![]() $\mathrm {Iso}(x)$
denotes an
$\mathrm {Iso}(x)$
denotes an
![]() $\mathcal {L}^+_\iota $
-formula expressing that x is an
$\mathcal {L}^+_\iota $
-formula expressing that x is an
![]() $\mathcal {L}^+$
-structure and that
$\mathcal {L}^+$
-structure and that
![]() $\iota $
is an
$\iota $
is an
![]() $\in $
-isomorphism from the universe V onto x. We shall study this axiom in
$\in $
-isomorphism from the universe V onto x. We shall study this axiom in
![]() $\mathcal {L}^+_{\iota , \mathsf {self}}$
:
$\mathcal {L}^+_{\iota , \mathsf {self}}$
:
(This formulation is chosen over
![]() $\exists x \hspace {2pt} \mathrm {Iso}(x)$
, as it is convenient to have a reference to a witness.)
$\exists x \hspace {2pt} \mathrm {Iso}(x)$
, as it is convenient to have a reference to a witness.)
By the
![]() $\in $
-isomorphism property, and the absoluteness of
$\in $
-isomorphism property, and the absoluteness of
![]() $\models $
for standard formulas, we have:
$\models $
for standard formulas, we have:
Proposition 2.16. For each
![]() $\phi (\vec {x}) \in \mathcal {L}$
,
$\phi (\vec {x}) \in \mathcal {L}$
,
![]() $\mathsf {ZF} + \mathrm {Iso}(\mathsf {self}) \vdash (\mathsf {self} \models \ulcorner \phi (\iota (\vec {x})) \urcorner ) \leftrightarrow \phi (\vec {x})$
.
$\mathsf {ZF} + \mathrm {Iso}(\mathsf {self}) \vdash (\mathsf {self} \models \ulcorner \phi (\iota (\vec {x})) \urcorner ) \leftrightarrow \phi (\vec {x})$
.
System 2.17. Let S be a set theory in
![]() $\mathcal {L}^+$
. By recursion, for each
$\mathcal {L}^+$
. By recursion, for each
![]() $\alpha \leq \omega $
, we define the system
$\alpha \leq \omega $
, we define the system
![]() $\mathsf {SP}^\alpha (S)$
(standing for Self-Perception):
$\mathsf {SP}^\alpha (S)$
(standing for Self-Perception):
 $$ \begin{align*} \mathsf{SP}^0(S) &=_{\mathrm{df}} \mathsf{GR}^0(S) = \mathsf{CT}(S) \hspace{-4pt}\restriction + \hspace{2pt} \mathsf{Sep}(\mathcal{L}^+_{\mathsf{Sat}}), \\ \mathsf{SP}^{\alpha+1}(S) &=_{\mathrm{df}} \mathsf{GR}^{\alpha+1}(S) + \mathsf{self} \in \mathbf{crsm} + \mathrm{Iso}(\mathsf{self}) + \mathsf{self} \models \mathbf{Tr} \cup \underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathsf{SP}}^{\underline{\alpha}}(\underset{\substack{\\[-9.5pt]\mbox{.}}}{S}), \\ \mathsf{SP}^\omega(S) &=_{\mathrm{df}} \bigcup_{n < \omega} \mathsf{SP}^n(S), \end{align*} $$
$$ \begin{align*} \mathsf{SP}^0(S) &=_{\mathrm{df}} \mathsf{GR}^0(S) = \mathsf{CT}(S) \hspace{-4pt}\restriction + \hspace{2pt} \mathsf{Sep}(\mathcal{L}^+_{\mathsf{Sat}}), \\ \mathsf{SP}^{\alpha+1}(S) &=_{\mathrm{df}} \mathsf{GR}^{\alpha+1}(S) + \mathsf{self} \in \mathbf{crsm} + \mathrm{Iso}(\mathsf{self}) + \mathsf{self} \models \mathbf{Tr} \cup \underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathsf{SP}}^{\underline{\alpha}}(\underset{\substack{\\[-9.5pt]\mbox{.}}}{S}), \\ \mathsf{SP}^\omega(S) &=_{\mathrm{df}} \bigcup_{n < \omega} \mathsf{SP}^n(S), \end{align*} $$
where
![]() $\mathbf {Tr} =_{\mathrm {df}} \{\sigma \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\sigma )\}$
. We write
$\mathbf {Tr} =_{\mathrm {df}} \{\sigma \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\sigma )\}$
. We write
![]() $\mathsf {SP}^\alpha $
for
$\mathsf {SP}^\alpha $
for
![]() $\mathsf {SP}^\alpha (\mathsf {ZF})$
.
$\mathsf {SP}^\alpha (\mathsf {ZF})$
.
Remark. A clarificatory note on the role of the languages in
![]() $\mathsf {SP}^\alpha $
. Let
$\mathsf {SP}^\alpha $
. Let
![]() $\alpha \geq 1$
. The language of
$\alpha \geq 1$
. The language of
![]() $\mathsf {SP}^\alpha $
is
$\mathsf {SP}^\alpha $
is
![]() $\mathcal {L}_{\mathsf {Sat}, \iota , \mathsf {self}}$
.
$\mathcal {L}_{\mathsf {Sat}, \iota , \mathsf {self}}$
.
![]() $\mathsf {SP}^\alpha $
proves Separation for
$\mathsf {SP}^\alpha $
proves Separation for
![]() $\mathcal {L}_{\mathsf {Sat}, \mathsf {self}}$
, and it proves Replacement for
$\mathcal {L}_{\mathsf {Sat}, \mathsf {self}}$
, and it proves Replacement for
![]() $\mathcal {L}_{\mathsf {self}}$
(since
$\mathcal {L}_{\mathsf {self}}$
(since
![]() $\mathsf {self}$
can be treated as a parameter in these schemas).
$\mathsf {self}$
can be treated as a parameter in these schemas).
Lemma 2.18. Let
![]() $\alpha \leq \omega $
. Every
$\alpha \leq \omega $
. Every
![]() $\text {crsm} \mathcal {U}$
of
$\text {crsm} \mathcal {U}$
of
![]() $\mathsf {GR}^\alpha $
expands to a model
$\mathsf {GR}^\alpha $
expands to a model
![]() $\mathcal {U}^*$
of
$\mathcal {U}^*$
of
![]() $\mathsf {SP}^\alpha $
. Moreover, if
$\mathsf {SP}^\alpha $
. Moreover, if
![]() $\mathcal {U}$
is a definable model, then we can also obtain that
$\mathcal {U}$
is a definable model, then we can also obtain that
![]() $\mathcal {U}^*$
is definable.
$\mathcal {U}^*$
is definable.
Proof. We start by showing the case
![]() $\alpha < \omega $
by induction. The base case
$\alpha < \omega $
by induction. The base case
![]() $\alpha = 0$
is trivial. The induction hypothesis is that if
$\alpha = 0$
is trivial. The induction hypothesis is that if
![]() $\mathcal {U} \models \mathsf {GR}^{\alpha }$
, then
$\mathcal {U} \models \mathsf {GR}^{\alpha }$
, then
![]() $\mathcal {U}$
expands to a model of
$\mathcal {U}$
expands to a model of
![]() $\mathsf {SP}^\alpha $
; and if
$\mathsf {SP}^\alpha $
; and if
![]() $\mathcal {U}$
is definable, then the expansion is definable. Let
$\mathcal {U}$
is definable, then the expansion is definable. Let
![]() $\mathcal {U} \models \mathsf {GR}^{\alpha + 1}$
. Applying Lemma 2.14, we find a
$\mathcal {U} \models \mathsf {GR}^{\alpha + 1}$
. Applying Lemma 2.14, we find a
![]() $\text {crsm} \mathcal {V}$
in
$\text {crsm} \mathcal {V}$
in
![]() $\mathcal {U}$
, such that
$\mathcal {U}$
, such that
![]() $\mathcal {U} \cong _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
(as witnessed by an
$\mathcal {U} \cong _{\mathcal {L}} \mathcal {V}_{\mathcal {U}}$
(as witnessed by an
![]() $\mathcal {L}$
-isomorphism
$\mathcal {L}$
-isomorphism
![]() $i : \mathcal {U} \rightarrow \mathcal {V}_{\mathcal {U}}$
) and
$i : \mathcal {U} \rightarrow \mathcal {V}_{\mathcal {U}}$
) and
![]() $\mathcal {U}$
satisfies that
$\mathcal {U}$
satisfies that
![]() $\mathcal {V} \models \mathbf {Tr} \cup \underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {GR}}^{\underline {\alpha }}$
. So by the induction hypothesis applied in
$\mathcal {V} \models \mathbf {Tr} \cup \underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {GR}}^{\underline {\alpha }}$
. So by the induction hypothesis applied in
![]() $\mathcal {U}$
,
$\mathcal {U}$
,
![]() $\mathcal {U}$
satisfies that
$\mathcal {U}$
satisfies that
![]() $\mathcal {V}$
expands to a model
$\mathcal {V}$
expands to a model
![]() $\mathcal {W}$
of
$\mathcal {W}$
of
![]() $\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {SP}}^{\underline {\alpha }}$
. Let
$\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {SP}}^{\underline {\alpha }}$
. Let
![]() $\mathcal {U}^*$
be the model obtained from
$\mathcal {U}^*$
be the model obtained from
![]() $\mathcal {U}$
by interpreting
$\mathcal {U}$
by interpreting
![]() $\mathsf {self}$
by
$\mathsf {self}$
by
![]() $\mathcal {W}$
and interpreting
$\mathcal {W}$
and interpreting
![]() $\iota $
by i. It is immediate from the construction that
$\iota $
by i. It is immediate from the construction that
![]() $\mathcal {U}^* \models \mathsf {SP}^{\alpha + 1}$
.
$\mathcal {U}^* \models \mathsf {SP}^{\alpha + 1}$
.
Now to the case that
![]() $\alpha = \omega $
: Assume that
$\alpha = \omega $
: Assume that
![]() $\mathcal {U} \models \mathsf {GR}^\omega $
. Working in
$\mathcal {U} \models \mathsf {GR}^\omega $
. Working in
![]() $\mathcal {U}$
, let
$\mathcal {U}$
, let
![]() $\mathbf {Tr} = \{\phi \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\phi )\}$
. By the above,
$\mathbf {Tr} = \{\phi \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\phi )\}$
. By the above,
is a recursive type over
![]() $\mathcal {U}$
. So since
$\mathcal {U}$
. So since
![]() $\mathcal {U}$
is recursively saturated, it is realized by some
$\mathcal {U}$
is recursively saturated, it is realized by some
![]() $\mathcal {W}$
in
$\mathcal {W}$
in
![]() $\mathcal {U}$
. It now follows from Lemma 2.13 that
$\mathcal {U}$
. It now follows from Lemma 2.13 that
![]() $\mathcal {U} \cong _{\mathcal {L}} \mathcal {W}_{\mathcal {U}}$
. So just as in the former case,
$\mathcal {U} \cong _{\mathcal {L}} \mathcal {W}_{\mathcal {U}}$
. So just as in the former case,
![]() $\mathcal {U}$
can be expanded to a model
$\mathcal {U}$
can be expanded to a model
![]() $\mathcal {U}^*$
of
$\mathcal {U}^*$
of
![]() $\mathsf {SP}^\omega $
.
$\mathsf {SP}^\omega $
.
Assume now that
![]() $\mathcal {U}$
is definable.
$\mathcal {U}$
is definable.
![]() $\mathcal {W}$
can then be defined as the least element of a definable enumeration of
$\mathcal {W}$
can then be defined as the least element of a definable enumeration of
![]() $\mathcal {U}$
that satisfies the appropriate conditions. An isomorphism witnessing
$\mathcal {U}$
that satisfies the appropriate conditions. An isomorphism witnessing
![]() $\mathcal {U} \cong _{\mathcal {L}} \mathcal {W}_{\mathcal {U}}$
can also be defined: As seen from a close look at the proof of Theorem 2.4, the isomorphism is constructed by recursion on enumerations of
$\mathcal {U} \cong _{\mathcal {L}} \mathcal {W}_{\mathcal {U}}$
can also be defined: As seen from a close look at the proof of Theorem 2.4, the isomorphism is constructed by recursion on enumerations of
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\mathcal {W}_{\mathcal {U}}$
, both of which can be chosen definable since
$\mathcal {W}_{\mathcal {U}}$
, both of which can be chosen definable since
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\mathcal {W}_{\mathcal {U}}$
are definable and countable.□
$\mathcal {W}_{\mathcal {U}}$
are definable and countable.□
Lemma 2.19.
![]() $\mathsf {GR}^\omega $
interprets
$\mathsf {GR}^\omega $
interprets
![]() $\mathsf {SP}^\omega $
.
$\mathsf {SP}^\omega $
.
Proof. Since
![]() $\mathsf {GR}^\omega $
is
$\mathsf {GR}^\omega $
is
![]() $\omega $
-inconsistent, there is a formula
$\omega $
-inconsistent, there is a formula
![]() such that
such that
![]() , but for each
, but for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() .
.
We start by working in
![]() $\mathsf {GR}^\omega $
. By
$\mathsf {GR}^\omega $
. By
![]() $\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
, the theory
$\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
, the theory
![]() $\mathbf {Tr} = \{\sigma \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\sigma )\}$
of truth is a set; and by the argument starting the proof of Lemma 2.14, it is a consistent theory. So there is a definable
$\mathbf {Tr} = \{\sigma \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\sigma )\}$
of truth is a set; and by the argument starting the proof of Lemma 2.14, it is a consistent theory. So there is a definable
![]() $\mathcal {S} \in \mathbf {crsm}$
that models truth.Footnote
9
Since
$\mathcal {S} \in \mathbf {crsm}$
that models truth.Footnote
9
Since
![]() $\mathcal {S}$
is a model of truth, the Global Reflection axioms allow us to prove
$\mathcal {S}$
is a model of truth, the Global Reflection axioms allow us to prove
![]() $\mathcal {S} \models \mathsf {GR}^{\underline {n}}$
, for each standard natural number n. Let
$\mathcal {S} \models \mathsf {GR}^{\underline {n}}$
, for each standard natural number n. Let
![]() $d < \omega $
be the minimal number such that
$d < \omega $
be the minimal number such that
![]() , and let c be the maximal number such that
, and let c be the maximal number such that
![]() $c \leq d$
and
$c \leq d$
and
![]() $\mathcal {S} \models \mathsf {GR}^c$
. Note that for each standard natural number n, we can prove
$\mathcal {S} \models \mathsf {GR}^c$
. Note that for each standard natural number n, we can prove
![]() $\underline {n} < c$
. By Lemma 2.18,
$\underline {n} < c$
. By Lemma 2.18,
![]() $\mathcal {S}$
expands to a definable model
$\mathcal {S}$
expands to a definable model
![]() $\mathcal {S}^{\prime }$
of
$\mathcal {S}^{\prime }$
of
![]() $\mathsf {SP}^c$
.
$\mathsf {SP}^c$
.
Working in the meta-theory, it follows that
![]() $\mathsf {GR}^\omega $
interprets
$\mathsf {GR}^\omega $
interprets
![]() $\mathsf {SP}^\omega $
by an interpretation
$\mathsf {SP}^\omega $
by an interpretation
![]() $\mathcal {J}$
mapping each sentence
$\mathcal {J}$
mapping each sentence
![]() $\sigma $
in the language of
$\sigma $
in the language of
![]() $\mathsf {SP}^\omega $
to the
$\mathsf {SP}^\omega $
to the
![]() $\mathcal {L}_{\mathsf {Sat}}$
-sentence
$\mathcal {L}_{\mathsf {Sat}}$
-sentence
![]() $\mathcal {S}^{\prime } \models \ulcorner \sigma \urcorner $
.□
$\mathcal {S}^{\prime } \models \ulcorner \sigma \urcorner $
.□
3 Revision-semantic truth-in-a-universe
We shall now go through the key revision-semantic technique introduced in this paper, which may be used to construct a variety of untyped truth-in-a-universe relations for the multiverse of set theory. Revision-semantics was independently invented in [Reference Gupta9]. In [Reference Friedman and Sheard5], the axiomatic theory of truth
![]() $\mathsf {FS}$
was presented and shown to be validated by a model constructed through such a revision process. The revision process starts with an arbitrary extension
$\mathsf {FS}$
was presented and shown to be validated by a model constructed through such a revision process. The revision process starts with an arbitrary extension
![]() $S_0$
of truth, and recursively defines
$S_0$
of truth, and recursively defines
![]() $S_{n + 1}$
as the theory of the structure
$S_{n + 1}$
as the theory of the structure
![]() $(\mathbb {N}, S_n)$
. In particular, the theory of
$(\mathbb {N}, S_n)$
. In particular, the theory of
![]() $\mathbb {N}$
is a subset of
$\mathbb {N}$
is a subset of
![]() $S_1$
, and the liar sentence is in
$S_1$
, and the liar sentence is in
![]() $S_{n+1}$
iff it is not in
$S_{n+1}$
iff it is not in
![]() $S_{n}$
.
$S_{n}$
.
The construction in this paper is somewhat different in that it is intensional. We start with a more-or-less arbitrary formula defining truth-in-a-universe, and revise the definition in a revision-semantic fashion. The construction can be modified by adjusting parameters. For example, we shall see that certain conditions on the parameters result in that the eventual definition of truth-in-a-universe validates the multiverse theory
![]() $\mathsf {MS}$
, introduced in System 4.5. This theory is analogous to
$\mathsf {MS}$
, introduced in System 4.5. This theory is analogous to
![]() $\mathsf {FS}$
, but is actually weaker. The parameters need to satisfy some basic conditions as specified in this definition:
$\mathsf {FS}$
, but is actually weaker. The parameters need to satisfy some basic conditions as specified in this definition:
Definition 3.1. Let
![]() $\mathrm {T}_n(\phi )$
,
$\mathrm {T}_n(\phi )$
,
![]() $\mathrm {Uni}_n(\mathcal {U})$
and
$\mathrm {Uni}_n(\mathcal {U})$
and
![]() $\mathrm {Mod}_0(\mathcal {U}, \phi , f)$
be formulas of the meta-language (
$\mathrm {Mod}_0(\mathcal {U}, \phi , f)$
be formulas of the meta-language (
![]() $\mathcal {L}$
), in the free variables
$\mathcal {L}$
), in the free variables
![]() $\{n, \phi \}$
,
$\{n, \phi \}$
,
![]() $\{n, \mathcal {U}\}$
and
$\{n, \mathcal {U}\}$
and
![]() $\{\mathcal {U}, \phi , f\}$
, respectively.Footnote
10
For each
$\{\mathcal {U}, \phi , f\}$
, respectively.Footnote
10
For each
![]() $n \in \mathbb {N}$
:
$n \in \mathbb {N}$
:
 $$ \begin{align*} \mathbf{T}_n &=_{\mathrm{df}} \{\phi \mid \mathrm{T}_n(\phi)\}, \\ \mathbf{T}_\omega &=_{\mathrm{df}} \bigcup_{n < \omega} \mathbf{T}_n, \\ \mathbf{Uni}_n &=_{\mathrm{df}} \{\mathcal{U} \mid \mathrm{Uni}_n(\mathcal{U})\}, \\ \mathbf{Uni}_\omega &=_{\mathrm{df}} \bigcap_{n < \omega} \mathbf{Uni}_n. \end{align*} $$
$$ \begin{align*} \mathbf{T}_n &=_{\mathrm{df}} \{\phi \mid \mathrm{T}_n(\phi)\}, \\ \mathbf{T}_\omega &=_{\mathrm{df}} \bigcup_{n < \omega} \mathbf{T}_n, \\ \mathbf{Uni}_n &=_{\mathrm{df}} \{\mathcal{U} \mid \mathrm{Uni}_n(\mathcal{U})\}, \\ \mathbf{Uni}_\omega &=_{\mathrm{df}} \bigcap_{n < \omega} \mathbf{Uni}_n. \end{align*} $$
![]() $(\mathbf {T}_n)_{n \in \mathbb {N}}$
is intended to be a sequence of first-order set theories, and
$(\mathbf {T}_n)_{n \in \mathbb {N}}$
is intended to be a sequence of first-order set theories, and
![]() $(\mathbf {Uni}_n)_{n \in \mathbb {N}}$
is intended to be a sequence of classes of models, as formally specified below. Let
$(\mathbf {Uni}_n)_{n \in \mathbb {N}}$
is intended to be a sequence of classes of models, as formally specified below. Let
![]() $\mathcal {L}^{\mathrm {T}}, \mathcal {L}^{\mathrm {Rev}}$
be recursive languages. We say that
$\mathcal {L}^{\mathrm {T}}, \mathcal {L}^{\mathrm {Rev}}$
be recursive languages. We say that
![]() $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
are revision parameters (in
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
are revision parameters (in
![]() $\mathcal {L}^{\mathrm {T}}, \mathcal {L}^{\mathrm {Rev}}$
) if the following conditions (closed under
$\mathcal {L}^{\mathrm {T}}, \mathcal {L}^{\mathrm {Rev}}$
) if the following conditions (closed under
![]() $\forall n \in \mathbb {N}$
, where appropriate) are provable in the meta-theory and in a given set theory (as object theory):
$\forall n \in \mathbb {N}$
, where appropriate) are provable in the meta-theory and in a given set theory (as object theory):
-
1.
 $\mathcal {L} \subseteq \mathcal {L}^{\mathrm {Rev}} \subseteq \mathcal {L}^{\mathrm {T}}$
.
$\mathcal {L} \subseteq \mathcal {L}^{\mathrm {Rev}} \subseteq \mathcal {L}^{\mathrm {T}}$
. -
2. “The symbols
 $\mathsf {Uni}, \mathsf {Mod}$
do not appear in
$\mathsf {Uni}, \mathsf {Mod}$
do not appear in
 $\mathcal {L}^{\mathrm {T}}$
.”
$\mathcal {L}^{\mathrm {T}}$
.” -
3. “
 $\mathbf {T}_0$
is a set theory in
$\mathbf {T}_0$
is a set theory in
 $\mathcal {L}^{\mathrm {T}}$
.”
$\mathcal {L}^{\mathrm {T}}$
.” -
4.
 $ \mathbf {T}_{n+1} \vdash \mathbf {T}_{n}. $
$ \mathbf {T}_{n+1} \vdash \mathbf {T}_{n}. $
-
5.
 $ \mathrm {Uni}_0(\mathcal {U}) \rightarrow x “\mathcal {U} \text {is an }\mathcal {L}^{\mathrm {T}}\text {-structure.”} $
$ \mathrm {Uni}_0(\mathcal {U}) \rightarrow x “\mathcal {U} \text {is an }\mathcal {L}^{\mathrm {T}}\text {-structure.”} $
-
6.
 $ \mathbf {Uni}_{n+1} \subseteq \mathbf {Uni}_n $
.
$ \mathbf {Uni}_{n+1} \subseteq \mathbf {Uni}_n $
. -
7.
 $ \mathrm {Mod}_0(\mathcal {U}, \phi , f) \rightarrow \mathrm {Uni}_0(\mathcal {U}) \wedge \phi \in \mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}} \wedge f \in \mathrm {VA}^{\mathcal {U}} $
.
$ \mathrm {Mod}_0(\mathcal {U}, \phi , f) \rightarrow \mathrm {Uni}_0(\mathcal {U}) \wedge \phi \in \mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}} \wedge f \in \mathrm {VA}^{\mathcal {U}} $
.
In the construction below we shall see how, given revision parameters, an untyped revision-semantic truth-in-a-universe predicate can be defined as an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\mathrm {Mod}_n(\mathcal {U}, \phi , f)$
, with this intended reading of the variables: n is the stage in the revision process,
$\mathrm {Mod}_n(\mathcal {U}, \phi , f)$
, with this intended reading of the variables: n is the stage in the revision process,
![]() $\mathcal {U}$
is a universe,
$\mathcal {U}$
is a universe,
![]() $\phi $
is a formula in (the representation of)
$\phi $
is a formula in (the representation of)
![]() $\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
and f is an assignment of variables to elements of
$\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
and f is an assignment of variables to elements of
![]() $\mathcal {U}$
. So
$\mathcal {U}$
. So
![]() $\mathcal {L}^{\mathrm {T}}$
is the language of the theories
$\mathcal {L}^{\mathrm {T}}$
is the language of the theories
![]() $\mathbf {T}_n$
,
$\mathbf {T}_n$
,
![]() $\mathcal {L}^{\mathrm {Rev}}$
is any sublanguage of
$\mathcal {L}^{\mathrm {Rev}}$
is any sublanguage of
![]() $\mathcal {L}^{\mathrm {T}}$
, and
$\mathcal {L}^{\mathrm {T}}$
, and
![]() $\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
is the language undergoing revision. The
$\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
is the language undergoing revision. The
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\mathrm {Mod}^\circlearrowright $
is also introduced as a variant of
$\mathrm {Mod}^\circlearrowright $
is also introduced as a variant of
![]() $\mathrm {Mod}_n$
. Actually, only the
$\mathrm {Mod}_n$
. Actually, only the
![]() $\mathrm {Uni}_n$
and
$\mathrm {Uni}_n$
and
![]() $\mathrm {Mod}_0$
parameters influence the construction. The
$\mathrm {Mod}_0$
parameters influence the construction. The
![]() $\mathrm {T}_n$
parameter comes into play later on, in the Main Lemma (in Section 5), where we show (under certain conditions on the revision parameters) that the
$\mathrm {T}_n$
parameter comes into play later on, in the Main Lemma (in Section 5), where we show (under certain conditions on the revision parameters) that the
![]() $\mathrm {Mod}_n$
formula satisfies desirable semantically motivated axioms when constructed in the theory
$\mathrm {Mod}_n$
formula satisfies desirable semantically motivated axioms when constructed in the theory
![]() $\mathbf {T}_\omega $
.
$\mathbf {T}_\omega $
.
The construction may intuitively be thought of as a recursive procedure, where
![]() $\mathrm {Mod}_0$
is a more-or-less arbitrary truth-in-a-universe relation and each
$\mathrm {Mod}_0$
is a more-or-less arbitrary truth-in-a-universe relation and each
![]() $\mathrm {Mod}_{n+1}$
revises
$\mathrm {Mod}_{n+1}$
revises
![]() $\mathrm {Mod}_n$
into a more adequate relation. It turns out to be efficient to perform the construction using Gödel’s fixed-point lemma. It is in fact possible to choose
$\mathrm {Mod}_n$
into a more adequate relation. It turns out to be efficient to perform the construction using Gödel’s fixed-point lemma. It is in fact possible to choose
![]() $\mathrm {Mod}_0$
such that it gets revised to itself (see the definition of
$\mathrm {Mod}_0$
such that it gets revised to itself (see the definition of
![]() $\mathrm {Mod}^\circlearrowright $
below). This phenomenon contrasts with the revision-semantics ordinarily used to construct a model of the Friedman–Sheard theory of truth, where the revision-operation has no fixed-point (see Lemma 14.9(iii) in [Reference Halbach11]). A key difference between the present revision-process and that one is that the former is intensional and the latter is extensional. In the present framework we start with an arbitrary formula defining truth-in-a-universe and revise it to more adequate definitions, while in the other framework one starts with an arbitrary extension of truth and revise it more adequate extensions. The move from extensional to intensional revision-semantics is highly relevant for the present framework.
$\mathrm {Mod}^\circlearrowright $
below). This phenomenon contrasts with the revision-semantics ordinarily used to construct a model of the Friedman–Sheard theory of truth, where the revision-operation has no fixed-point (see Lemma 14.9(iii) in [Reference Halbach11]). A key difference between the present revision-process and that one is that the former is intensional and the latter is extensional. In the present framework we start with an arbitrary formula defining truth-in-a-universe and revise it to more adequate definitions, while in the other framework one starts with an arbitrary extension of truth and revise it more adequate extensions. The move from extensional to intensional revision-semantics is highly relevant for the present framework.
Construction 3.2 (Construction of Revision-semantics for the Multiverse)
Let
![]() $\mathrm {T}_n(\phi )$
,
$\mathrm {T}_n(\phi )$
,
![]() $\mathrm {Uni}_n(\mathcal {U})$
and
$\mathrm {Uni}_n(\mathcal {U})$
and
![]() $\mathrm {Mod}_0(\mathcal {U}, \phi , f)$
be revision parameters.
$\mathrm {Mod}_0(\mathcal {U}, \phi , f)$
be revision parameters.
By Gödel’s fixed-point lemma, there is an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\mathrm {Mod}_n(\mathcal {U}, \phi , f)$
, in the free variables
$\mathrm {Mod}_n(\mathcal {U}, \phi , f)$
, in the free variables
![]() $n,\mathcal {U}, \phi , f$
, such that provably:
$n,\mathcal {U}, \phi , f$
, such that provably:
 $$ \begin{align} \mathrm{Mod}_n(\mathcal{U}, \phi, f) \leftrightarrow \left( \begin{aligned} & n \in \mathbb{N} \wedge \mathrm{Uni}_n(\mathcal{U}) \wedge \phi \in \mathcal{L}^{\mathrm{Rev}}_{\mathsf{Uni}, \mathsf{Mod}} \wedge f \in \mathrm{VA}^{\mathcal{U}} \\ \wedge & \big(n = 0 \rightarrow \mathrm{Mod}_0(\mathcal{U}, \phi, f) \big) \\ \wedge & \big( n>0 \rightarrow \langle \mathcal{U}\hspace{-4pt}\restriction_{\mathcal{L}^{\mathrm{Rev}}}, \ulcorner \mathrm{Uni}_{\underline{n-1}} \urcorner^{\mathcal{U}}, \ulcorner \mathrm{Mod}_{\underline{n-1}} \urcorner^{\mathcal{U}} \rangle \models (\phi, f) \big) \end{aligned} \right). \end{align} $$
$$ \begin{align} \mathrm{Mod}_n(\mathcal{U}, \phi, f) \leftrightarrow \left( \begin{aligned} & n \in \mathbb{N} \wedge \mathrm{Uni}_n(\mathcal{U}) \wedge \phi \in \mathcal{L}^{\mathrm{Rev}}_{\mathsf{Uni}, \mathsf{Mod}} \wedge f \in \mathrm{VA}^{\mathcal{U}} \\ \wedge & \big(n = 0 \rightarrow \mathrm{Mod}_0(\mathcal{U}, \phi, f) \big) \\ \wedge & \big( n>0 \rightarrow \langle \mathcal{U}\hspace{-4pt}\restriction_{\mathcal{L}^{\mathrm{Rev}}}, \ulcorner \mathrm{Uni}_{\underline{n-1}} \urcorner^{\mathcal{U}}, \ulcorner \mathrm{Mod}_{\underline{n-1}} \urcorner^{\mathcal{U}} \rangle \models (\phi, f) \big) \end{aligned} \right). \end{align} $$
Recall that if
![]() $\phi (\vec {x})$
is a formula in the language of a structure
$\phi (\vec {x})$
is a formula in the language of a structure
![]() $\mathcal {M}$
, then
$\mathcal {M}$
, then
![]() $\phi ^{\mathcal {M}} = \{\vec {a} \in \mathcal {M} \mid \mathcal {M} \models \phi (\vec {a})\}$
. Above, this notation is used for formulas in a represented language, hence the Gödel quotes,
$\phi ^{\mathcal {M}} = \{\vec {a} \in \mathcal {M} \mid \mathcal {M} \models \phi (\vec {a})\}$
. Above, this notation is used for formulas in a represented language, hence the Gödel quotes,
![]() $\ulcorner \urcorner $
. Working in
$\ulcorner \urcorner $
. Working in
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $\langle \mathcal {U}\hspace {-4pt}\restriction _{\mathcal {L}^{\mathrm {Rev}}}, \ulcorner \mathrm {Uni}_{\underline {n-1}} \urcorner ^{\mathcal {U}}, \ulcorner \mathrm {Mod}_{\underline {n-1}} \urcorner ^{\mathcal {U}} \rangle $
is the expansion of
$\langle \mathcal {U}\hspace {-4pt}\restriction _{\mathcal {L}^{\mathrm {Rev}}}, \ulcorner \mathrm {Uni}_{\underline {n-1}} \urcorner ^{\mathcal {U}}, \ulcorner \mathrm {Mod}_{\underline {n-1}} \urcorner ^{\mathcal {U}} \rangle $
is the expansion of
![]() $\mathcal {U}\hspace {-4pt}\restriction _{\mathcal {L}^{\mathrm {Rev}}}$
to
$\mathcal {U}\hspace {-4pt}\restriction _{\mathcal {L}^{\mathrm {Rev}}}$
to
![]() $\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
, interpreting
$\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
, interpreting
![]() $\ulcorner \mathsf {Mod} \urcorner $
by
$\ulcorner \mathsf {Mod} \urcorner $
by
![]() $\{\vec {a} \in \mathcal {U} \mid \mathcal {U} \models \ulcorner \mathrm {Mod}_{\underline {n-1}} \urcorner (\vec {a})\}$
, and interpreting
$\{\vec {a} \in \mathcal {U} \mid \mathcal {U} \models \ulcorner \mathrm {Mod}_{\underline {n-1}} \urcorner (\vec {a})\}$
, and interpreting
![]() $\ulcorner \mathsf {Uni} \urcorner $
by
$\ulcorner \mathsf {Uni} \urcorner $
by
![]() $\{u \in \mathcal {U} \mid \mathcal {U} \models \ulcorner \mathrm {Uni}_{\underline {n-1}} \urcorner (u)\}$
.
$\{u \in \mathcal {U} \mid \mathcal {U} \models \ulcorner \mathrm {Uni}_{\underline {n-1}} \urcorner (u)\}$
.
Formally, we now have two references for the expression “
![]() $\mathrm {Mod}_0$
,” the formula
$\mathrm {Mod}_0$
,” the formula
![]() $\mathrm {Mod}_0$
and the formula
$\mathrm {Mod}_0$
and the formula
![]() $\mathrm {Mod}_n$
, with the variable assignment
$\mathrm {Mod}_n$
, with the variable assignment
![]() $n \mapsto 0$
. However, it is clear that these are equivalent.
$n \mapsto 0$
. However, it is clear that these are equivalent.
The above construction works for a very wide range of choices for
![]() $\mathrm {Mod}_0$
. But by the fixed-point lemma, we can choose
$\mathrm {Mod}_0$
. But by the fixed-point lemma, we can choose
![]() $\mathrm {Mod}_0$
to be “equivalent to its own revision,” so that
$\mathrm {Mod}_0$
to be “equivalent to its own revision,” so that
![]() $\mathrm {Mod}_n$
turns out to be constant with respect to n. Indeed, there is an
$\mathrm {Mod}_n$
turns out to be constant with respect to n. Indeed, there is an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\mathrm {Mod}^\circlearrowright $
, such that provably:
$\mathrm {Mod}^\circlearrowright $
, such that provably:
 $$ \begin{align*} \mathrm{Mod}^\circlearrowright(\mathcal{U}, \phi, f) \leftrightarrow \left( \begin{aligned} & \mathrm{Uni}_0(\mathcal{U}) \wedge \phi \in \mathcal{L}^{\mathrm{Rev}}_{\mathsf{Uni}, \mathsf{Mod}} \wedge f \in \mathrm{VA}^{\mathcal{U}} \\ \wedge & \langle \mathcal{U}\hspace{-4pt}\restriction_{\mathcal{L}^{\mathrm{Rev}}}, \ulcorner \mathrm{Uni}_{\underline{0}} \urcorner^{\mathcal{U}}, \ulcorner \mathrm{Mod}^\circlearrowright \urcorner^{\mathcal{U}} \rangle \models (\phi, f) \end{aligned} \right) \end{align*} $$
$$ \begin{align*} \mathrm{Mod}^\circlearrowright(\mathcal{U}, \phi, f) \leftrightarrow \left( \begin{aligned} & \mathrm{Uni}_0(\mathcal{U}) \wedge \phi \in \mathcal{L}^{\mathrm{Rev}}_{\mathsf{Uni}, \mathsf{Mod}} \wedge f \in \mathrm{VA}^{\mathcal{U}} \\ \wedge & \langle \mathcal{U}\hspace{-4pt}\restriction_{\mathcal{L}^{\mathrm{Rev}}}, \ulcorner \mathrm{Uni}_{\underline{0}} \urcorner^{\mathcal{U}}, \ulcorner \mathrm{Mod}^\circlearrowright \urcorner^{\mathcal{U}} \rangle \models (\phi, f) \end{aligned} \right) \end{align*} $$
End of Construction.
For the reader familiar with the extensional revision-procedure used to construct a model of
![]() $\mathsf {FS}$
(this construction is reasonably well-known for
$\mathsf {FS}$
(this construction is reasonably well-known for
![]() $\mathsf {FS}$
formulated over
$\mathsf {FS}$
formulated over
![]() $\mathsf {PA}$
, see [Reference Halbach11, chap. Reference Herzberger13.1] for a detailed treatment), note how the recursive call in the fixed-point formula of our construction operates on an intension (the formula
$\mathsf {PA}$
, see [Reference Halbach11, chap. Reference Herzberger13.1] for a detailed treatment), note how the recursive call in the fixed-point formula of our construction operates on an intension (the formula
![]() $\mathrm {Mod}$
), which is interpreted in internal models. In contrast, the recursive call of the revision procedure for constructing a model of
$\mathrm {Mod}$
), which is interpreted in internal models. In contrast, the recursive call of the revision procedure for constructing a model of
![]() $\mathsf {FS}$
(say as a theory of truth over arithmetic) operates on an extension (the set of true sentences from the previous step), which is obtained from the external model. The authors take this to explain why it is possible to define a truth-in-a-universe relation
$\mathsf {FS}$
(say as a theory of truth over arithmetic) operates on an extension (the set of true sentences from the previous step), which is obtained from the external model. The authors take this to explain why it is possible to define a truth-in-a-universe relation
![]() $\mathrm {Mod}^\circlearrowright $
which is fixed by the revision-procedure. In the extensional revision-semantics, this is not possible simply because the liar sentence must switch truth-value in the external model at every step of the revision.
$\mathrm {Mod}^\circlearrowright $
which is fixed by the revision-procedure. In the extensional revision-semantics, this is not possible simply because the liar sentence must switch truth-value in the external model at every step of the revision.
Necessity was the mother of the intensional revision-semantics of this paper; the authors do not see any way to construct models of “the Copernican multiverse of sets” (as formalized by various theories in this paper, e.g.,
![]() $\mathsf {CM} + \textsf {Non-Triviality} + \mathsf {NEC}$
) by the extensional approach. Conversely, the authors do not see that the intensional approach can replace the extensional approach, as the former relies on that the intension acted upon in the recursive call is interpreted in an internal model. For arithmetic this may be a serious obstacle, as arithmetic does not have that kind of internal models.
$\mathsf {CM} + \textsf {Non-Triviality} + \mathsf {NEC}$
) by the extensional approach. Conversely, the authors do not see that the intensional approach can replace the extensional approach, as the former relies on that the intension acted upon in the recursive call is interpreted in an internal model. For arithmetic this may be a serious obstacle, as arithmetic does not have that kind of internal models.
Some conditions and rules for revision parameters, relevant for showing that the
![]() $\mathrm {Mod}_n$
formula constructed as above satisfies a desirable semantically motivated theory (see the Main Lemma in Section 5), are shown in Figure 1. If one of the rules holds, we say that the revision parameters admit it. Essentially, if the revision parameters admit
$\mathrm {Mod}_n$
formula constructed as above satisfies a desirable semantically motivated theory (see the Main Lemma in Section 5), are shown in Figure 1. If one of the rules holds, we say that the revision parameters admit it. Essentially, if the revision parameters admit
![]() $\mathsf {NEC}^*$
or
$\mathsf {NEC}^*$
or
![]() $\mathsf {CONEC}^*$
, then the multiverse theory interpreted admits
$\mathsf {CONEC}^*$
, then the multiverse theory interpreted admits
![]() $\mathsf {NEC}$
or
$\mathsf {NEC}$
or
![]() $\mathsf {CONEC}$
, respectively. In practice it is often easier to work with the other rule and conditions in Figure 1, using this lemma:
$\mathsf {CONEC}$
, respectively. In practice it is often easier to work with the other rule and conditions in Figure 1, using this lemma:

Fig. 1 Rules and conditions for the revision parameters.
Lemma 3.3. Let
![]() $\mathrm{ T}, \mathrm{ Uni}, \mathrm{ Mod}_0$
be revision parameters.
$\mathrm{ T}, \mathrm{ Uni}, \mathrm{ Mod}_0$
be revision parameters.
-
(a) If
 $\textsf {Soundness}^*$
is provable, then the parameters admit
$\textsf {Soundness}^*$
is provable, then the parameters admit
 $\mathsf {NEC}^*$
.
$\mathsf {NEC}^*$
. -
(b) If
 $\textsf {Completeness}^*$
is provable and the parameters admit the
$\textsf {Completeness}^*$
is provable and the parameters admit the
 $\textsf {Reflection rule}^*$
, then the parameters admit
$\textsf {Reflection rule}^*$
, then the parameters admit
 $\mathsf {CONEC}^*$
.
$\mathsf {CONEC}^*$
.
Proof.
-
(a) Let
 $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
 $\phi \in \mathcal {L}^{\mathrm {Rev}}$
. Assume that
$\phi \in \mathcal {L}^{\mathrm {Rev}}$
. Assume that
 $\textsf {Soundness}^*$
is provable (in the meta-theory
$\textsf {Soundness}^*$
is provable (in the meta-theory
 $\mathsf {ZF}$
) and that
$\mathsf {ZF}$
) and that
 $\mathbf {T}_n \vdash \phi $
. By the latter, encoding the proof in
$\mathbf {T}_n \vdash \phi $
. By the latter, encoding the proof in
 $\mathsf {ZF}$
, we have
$\mathsf {ZF}$
, we have
 $\mathsf {ZF} \vdash \Pr _{\mathbf {T}_n}(\ulcorner \phi \urcorner )$
. Combining these, we get
$\mathsf {ZF} \vdash \Pr _{\mathbf {T}_n}(\ulcorner \phi \urcorner )$
. Combining these, we get
 $\mathsf {ZF} \vdash \forall \mathcal {U} \in \mathbf {Uni}_{n+1} \hspace {2pt} (\mathcal {U} \models \ulcorner \phi \urcorner ))$
. Since
$\mathsf {ZF} \vdash \forall \mathcal {U} \in \mathbf {Uni}_{n+1} \hspace {2pt} (\mathcal {U} \models \ulcorner \phi \urcorner ))$
. Since
 $\mathbf {T}_{n+1} \vdash \mathsf {ZF}$
, we are done.
$\mathbf {T}_{n+1} \vdash \mathsf {ZF}$
, we are done. -
(b) Let
 $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
 $\phi \in \mathcal {L}^{\mathrm {Rev}}$
. Assume that
$\phi \in \mathcal {L}^{\mathrm {Rev}}$
. Assume that
 $\textsf {Completeness}^*$
is provable and the parameters admit the
$\textsf {Completeness}^*$
is provable and the parameters admit the
 $\textsf {Reflection rule}^*$
. Since
$\textsf {Reflection rule}^*$
. Since
 $\mathbf {T}_{n+1} \vdash \mathsf {ZF}$
, we have
$\mathbf {T}_{n+1} \vdash \mathsf {ZF}$
, we have
 $\mathbf {T}_{n+1} \vdash \textsf { Completeness}^*$
. Now suppose that
$\mathbf {T}_{n+1} \vdash \textsf { Completeness}^*$
. Now suppose that
 $\mathbf {T}_{n+1} \vdash \forall \mathcal {U} \in \mathbf {Uni}_{n+1} \hspace {2pt} (\mathcal {U} \models \ulcorner \phi \urcorner )$
. Then
$\mathbf {T}_{n+1} \vdash \forall \mathcal {U} \in \mathbf {Uni}_{n+1} \hspace {2pt} (\mathcal {U} \models \ulcorner \phi \urcorner )$
. Then
 $\mathbf {T}_{n+1} \vdash \Pr _{\mathbf {T}_n}(\ulcorner \phi \urcorner )$
. So by the
$\mathbf {T}_{n+1} \vdash \Pr _{\mathbf {T}_n}(\ulcorner \phi \urcorner )$
. So by the
 $\textsf {Reflection rule}^*$
,
$\textsf {Reflection rule}^*$
,
 $\mathbf {T}_{n+2} \vdash \phi $
, as desired. here
$\mathbf {T}_{n+2} \vdash \phi $
, as desired. here
□
4 Theories of untyped satisfaction for the multiverse
Section 3 showed how a revision-semantic relation of truth-in-a-universe can be constructed in set theory. We turn now to the task of finding appropriate axioms for truth-in-a-universe that are validated by such revision-constructions.
System 4.1 (
 $\mathsf {CM}$
)
$\mathsf {CM}$
)
![]() $\mathsf {CM}^-$
, standing for Compositional satisfaction for the Multiverse, is axiomatized as follows:
$\mathsf {CM}^-$
, standing for Compositional satisfaction for the Multiverse, is axiomatized as follows:
 $$ \begin{align*} \begin{array}{ll} \mathsf{Base} & \mathsf{ZF} + \mathsf{Sep}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) + \mathsf{Rep}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}), \\ \mathsf{CM}_= & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \forall f \in \mathrm{VA}^{\mathcal{U}} \hspace{2pt} \big(\mathsf{Mod}(\mathcal{U}, \ulcorner x = y \urcorner, f) \leftrightarrow f(x) = f(y))\big), \\ \mathsf{CM}_\neg & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \forall \phi \in \mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}} \hspace{2pt} \forall f \in \mathrm{VA}^{\mathcal{U}} \hspace{2pt} \big(\mathsf{Mod}(\mathcal{U}, \underset{\substack{\\[-9.5pt]\mbox{.}}}{\neg}\phi, f) \leftrightarrow \neg \mathsf{Mod}(\mathcal{U}, \phi, f) \big), \\ \mathsf{CM}_\wedge & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \forall \phi, \psi \in \mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}} \hspace{2pt} \forall f \in \mathrm{VA}^{\mathcal{U}} \hspace{2pt} \big(\mathsf{Mod}(\mathcal{U}, \phi \underset{\substack{\\[-9.5pt]\mbox{.}}}{\wedge} \psi, f) \leftrightarrow (\mathsf{Mod}(\mathcal{U}, \phi, f) \wedge \mathsf{Mod}(\mathcal{U}, \psi, f)) \big), \\ \mathsf{CM}_\forall & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \forall \phi \in \mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}} \hspace{2pt} \forall f \in \mathrm{VA}^{\mathcal{U}} \hspace{2pt} \big(\mathsf{Mod}(\mathcal{U}, \underset{\substack{\\[-9.5pt]\mbox{.}}}{\forall} u \hspace{2pt} \phi, f) \leftrightarrow \forall g \in \mathrm{VA}^{\mathcal{U}}_{f, u} \hspace{2pt} \mathsf{Mod}(\mathcal{U}, \phi, g) \big). \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathsf{Base} & \mathsf{ZF} + \mathsf{Sep}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) + \mathsf{Rep}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}), \\ \mathsf{CM}_= & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \forall f \in \mathrm{VA}^{\mathcal{U}} \hspace{2pt} \big(\mathsf{Mod}(\mathcal{U}, \ulcorner x = y \urcorner, f) \leftrightarrow f(x) = f(y))\big), \\ \mathsf{CM}_\neg & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \forall \phi \in \mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}} \hspace{2pt} \forall f \in \mathrm{VA}^{\mathcal{U}} \hspace{2pt} \big(\mathsf{Mod}(\mathcal{U}, \underset{\substack{\\[-9.5pt]\mbox{.}}}{\neg}\phi, f) \leftrightarrow \neg \mathsf{Mod}(\mathcal{U}, \phi, f) \big), \\ \mathsf{CM}_\wedge & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \forall \phi, \psi \in \mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}} \hspace{2pt} \forall f \in \mathrm{VA}^{\mathcal{U}} \hspace{2pt} \big(\mathsf{Mod}(\mathcal{U}, \phi \underset{\substack{\\[-9.5pt]\mbox{.}}}{\wedge} \psi, f) \leftrightarrow (\mathsf{Mod}(\mathcal{U}, \phi, f) \wedge \mathsf{Mod}(\mathcal{U}, \psi, f)) \big), \\ \mathsf{CM}_\forall & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \forall \phi \in \mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}} \hspace{2pt} \forall f \in \mathrm{VA}^{\mathcal{U}} \hspace{2pt} \big(\mathsf{Mod}(\mathcal{U}, \underset{\substack{\\[-9.5pt]\mbox{.}}}{\forall} u \hspace{2pt} \phi, f) \leftrightarrow \forall g \in \mathrm{VA}^{\mathcal{U}}_{f, u} \hspace{2pt} \mathsf{Mod}(\mathcal{U}, \phi, g) \big). \\ \end{array} \end{align*} $$
Define
![]() $\mathsf {ZF}_{\mathsf {Uni}, \mathsf {Mod}} =_{\mathrm {df}} \mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
. We write
$\mathsf {ZF}_{\mathsf {Uni}, \mathsf {Mod}} =_{\mathrm {df}} \mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
. We write
![]() $\mathsf {CM}$
for
$\mathsf {CM}$
for
![]() $\mathsf {CM}^-$
plus the axiom:
$\mathsf {CM}^-$
plus the axiom:
If
![]() $\mathcal {L}^{\prime }$
expands
$\mathcal {L}^{\prime }$
expands
![]() $\mathcal {L}$
, then we write
$\mathcal {L}$
, then we write
![]() $\mathsf {CM}^-(\mathcal {L}^{\prime })$
and
$\mathsf {CM}^-(\mathcal {L}^{\prime })$
and
![]() $\mathsf {CM}(\mathcal {L}^{\prime })$
for the corresponding systems obtained by replacing all occurrences of
$\mathsf {CM}(\mathcal {L}^{\prime })$
for the corresponding systems obtained by replacing all occurrences of
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
in the axioms of the form
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
in the axioms of the form
![]() $\mathsf {CM}_-$
above by the language
$\mathsf {CM}_-$
above by the language
![]() $\mathcal {L}^{\prime }_{\mathsf {Uni}, \mathsf {Mod}}$
. (So the Separation and Replacement schemas remain unchanged, ranging only over
$\mathcal {L}^{\prime }_{\mathsf {Uni}, \mathsf {Mod}}$
. (So the Separation and Replacement schemas remain unchanged, ranging only over
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
.)
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
.)
Remark. The natural analogue axioms
![]() $\mathsf {CM}_\vee , \mathsf {CM}_\rightarrow , \mathsf {CM}_\exists $
are easily derived in
$\mathsf {CM}_\vee , \mathsf {CM}_\rightarrow , \mathsf {CM}_\exists $
are easily derived in
![]() $\mathsf {CM}^-$
.
$\mathsf {CM}^-$
.
Remark. In
![]() $\mathsf {CM}^-$
, each
$\mathsf {CM}^-$
, each
![]() $\mathcal {U} \in \mathsf {Uni}$
may be viewed as an
$\mathcal {U} \in \mathsf {Uni}$
may be viewed as an
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-structure, by performing this assignment:
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-structure, by performing this assignment:
 $$ \begin{align*} \in^{\mathcal{U}} &=_{\mathrm{df}} \big\{\langle a, b \rangle \mid \mathsf{Mod}(\mathcal{U}, \ulcorner x \in y \urcorner, \langle x, y \rangle \mapsto \langle a, b \rangle)\big\}, \\ \mathsf{Uni}^{\mathcal{U}} &=_{\mathrm{df}} \big\{a \mid \mathsf{Mod}(\mathcal{U}, \ulcorner \mathsf{Uni}(x) \urcorner, x \mapsto a)\big\}, \\ \mathsf{Mod}^{\mathcal{U}} &=_{\mathrm{df}} \big\{\langle a, b, c \rangle \mid \mathsf{Mod}(\mathcal{U}, \ulcorner \mathsf{Mod}(x, y, z) \urcorner, \langle x, y, z \rangle \mapsto \langle a, b, c \rangle)\big\}. \end{align*} $$
$$ \begin{align*} \in^{\mathcal{U}} &=_{\mathrm{df}} \big\{\langle a, b \rangle \mid \mathsf{Mod}(\mathcal{U}, \ulcorner x \in y \urcorner, \langle x, y \rangle \mapsto \langle a, b \rangle)\big\}, \\ \mathsf{Uni}^{\mathcal{U}} &=_{\mathrm{df}} \big\{a \mid \mathsf{Mod}(\mathcal{U}, \ulcorner \mathsf{Uni}(x) \urcorner, x \mapsto a)\big\}, \\ \mathsf{Mod}^{\mathcal{U}} &=_{\mathrm{df}} \big\{\langle a, b, c \rangle \mid \mathsf{Mod}(\mathcal{U}, \ulcorner \mathsf{Mod}(x, y, z) \urcorner, \langle x, y, z \rangle \mapsto \langle a, b, c \rangle)\big\}. \end{align*} $$
Accordingly, we will occasionally use the notation
![]() $\mathcal {U} \models \phi $
for satisfaction in that
$\mathcal {U} \models \phi $
for satisfaction in that
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-structure. Using the compositional axioms of
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-structure. Using the compositional axioms of
![]() $\mathsf {CM}^-$
, it is easily shown that
$\mathsf {CM}^-$
, it is easily shown that
![]() $\mathsf {Mod}(\mathcal {U}, \phi , f) \iff \mathcal {U} \models (\phi , f)$
.
$\mathsf {Mod}(\mathcal {U}, \phi , f) \iff \mathcal {U} \models (\phi , f)$
.
In applications, it is natural to add further axioms to
![]() $\mathsf {CM}^-$
, ensuring, e.g., that we can prove:
$\mathsf {CM}^-$
, ensuring, e.g., that we can prove:
Note that over
![]() $\mathsf {CM}^-$
, Non-Triviality is equivalent to
$\mathsf {CM}^-$
, Non-Triviality is equivalent to
![]() $\mathsf {Tr}^\Box (\ulcorner \bot \urcorner ) \rightarrow \bot $
. Recall that the formulas
$\mathsf {Tr}^\Box (\ulcorner \bot \urcorner ) \rightarrow \bot $
. Recall that the formulas
![]() $\mathsf {Tr}^\Box (\sigma )$
and
$\mathsf {Tr}^\Box (\sigma )$
and
![]() $\mathsf {Tr}^\Diamond (\sigma )$
are defined as
$\mathsf {Tr}^\Diamond (\sigma )$
are defined as
![]() $\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} (\mathsf {Mod}(\mathcal {U}, \sigma ))$
and
$\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} (\mathsf {Mod}(\mathcal {U}, \sigma ))$
and
![]() $\neg \mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma )$
, respectively. We may naturally consider the interpretation of the modal operators
$\neg \mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\neg }\sigma )$
, respectively. We may naturally consider the interpretation of the modal operators
![]() $\Box , \Diamond $
, generated by interpreting
$\Box , \Diamond $
, generated by interpreting
![]() $\Box \sigma $
by
$\Box \sigma $
by
![]() $\mathsf {Tr}^\Box (\ulcorner \sigma \urcorner )$
. Therefore, it is useful to exhibit some compositional conditions easily provable for
$\mathsf {Tr}^\Box (\ulcorner \sigma \urcorner )$
. Therefore, it is useful to exhibit some compositional conditions easily provable for
![]() $\mathsf {Tr}^\Box $
in
$\mathsf {Tr}^\Box $
in
![]() $\mathsf {CM}^-$
and
$\mathsf {CM}^-$
and
![]() $\mathsf {CM}^- + \textsf {Non-triviality}$
:
$\mathsf {CM}^- + \textsf {Non-triviality}$
:
Proposition 4.2.
![]() $\mathsf {CM}^-$
proves:
$\mathsf {CM}^-$
proves:
 $$ \begin{align*} \begin{array}{ll} \mathsf{CM}^\Box_\rightarrow & \forall \phi, \psi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\phi \underset{\substack{\\[-9.5pt]\mbox{.}}}{\rightarrow} \psi) \rightarrow (\mathsf{Tr}^\Box(\phi) \rightarrow \mathsf{Tr}^\Box(\psi)) \big), \\ \mathsf{CM}^\Box_\leftrightarrow & \forall \phi, \psi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\phi \underset{\substack{\\[-9.5pt]\mbox{.}}}{\leftrightarrow} \psi) \rightarrow (\mathsf{Tr}^\Box(\phi) \leftrightarrow \mathsf{Tr}^\Box(\psi)) \big),\\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathsf{CM}^\Box_\rightarrow & \forall \phi, \psi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\phi \underset{\substack{\\[-9.5pt]\mbox{.}}}{\rightarrow} \psi) \rightarrow (\mathsf{Tr}^\Box(\phi) \rightarrow \mathsf{Tr}^\Box(\psi)) \big), \\ \mathsf{CM}^\Box_\leftrightarrow & \forall \phi, \psi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\phi \underset{\substack{\\[-9.5pt]\mbox{.}}}{\leftrightarrow} \psi) \rightarrow (\mathsf{Tr}^\Box(\phi) \leftrightarrow \mathsf{Tr}^\Box(\psi)) \big),\\ \end{array} \end{align*} $$
 $$ \begin{align*} \begin{array}{ll} \mathsf{CM}^\Box_\wedge & \forall \phi, \psi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\phi \underset{\substack{\\[-9.5pt]\mbox{.}}}{\wedge} \psi) \leftrightarrow (\mathsf{Tr}^\Box(\phi) \wedge \mathsf{Tr}^\Box(\psi)) \big), \\ \Diamond_{\mathsf{CM}} & \forall \phi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Diamond(\phi) \leftrightarrow \exists \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \mathsf{Mod}(\mathcal{U}, \phi) \big). \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathsf{CM}^\Box_\wedge & \forall \phi, \psi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\phi \underset{\substack{\\[-9.5pt]\mbox{.}}}{\wedge} \psi) \leftrightarrow (\mathsf{Tr}^\Box(\phi) \wedge \mathsf{Tr}^\Box(\psi)) \big), \\ \Diamond_{\mathsf{CM}} & \forall \phi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Diamond(\phi) \leftrightarrow \exists \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \mathsf{Mod}(\mathcal{U}, \phi) \big). \\ \end{array} \end{align*} $$
Proposition 4.3.
![]() $\mathsf {CM}^- + \textsf {Non-Triviality}$
proves:
$\mathsf {CM}^- + \textsf {Non-Triviality}$
proves:
 $$ \begin{align*} \begin{array}{ll} \mathsf{CM}^\Box_\bot & \mathsf{Tr}^\Box(\ulcorner \bot \urcorner) \leftrightarrow \bot, \\ \mathsf{CM}^\Box_\neg & \forall \phi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\neg} \phi) \rightarrow \neg \mathsf{Tr}^\Box(\phi) \big), \\ \mathsf{D}_{\mathsf{CM}} & \forall \phi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\phi) \rightarrow \mathsf{Tr}^\Diamond(\phi) \big). \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathsf{CM}^\Box_\bot & \mathsf{Tr}^\Box(\ulcorner \bot \urcorner) \leftrightarrow \bot, \\ \mathsf{CM}^\Box_\neg & \forall \phi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\neg} \phi) \rightarrow \neg \mathsf{Tr}^\Box(\phi) \big), \\ \mathsf{D}_{\mathsf{CM}} & \forall \phi \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} \big( \mathsf{Tr}^\Box(\phi) \rightarrow \mathsf{Tr}^\Diamond(\phi) \big). \\ \end{array} \end{align*} $$
Lemma 4.4 (Soundness Lemma)
![]() $\mathsf {CM}^-$
proves that for all
$\mathsf {CM}^-$
proves that for all
![]() $\mathcal {U} \in \mathsf {Uni}$
,
$\mathcal {U} \in \mathsf {Uni}$
,
![]() $\{ \phi \in \mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}} \mid \mathsf {Mod}(\mathcal {U}, \phi ) \}$
is deductively closed.
$\{ \phi \in \mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}} \mid \mathsf {Mod}(\mathcal {U}, \phi ) \}$
is deductively closed.
Proof. Using the compositional axioms
![]() $\mathsf {CM}_\neg $
,
$\mathsf {CM}_\neg $
,
![]() $\mathsf {CM}_\wedge $
and
$\mathsf {CM}_\wedge $
and
![]() $\mathsf {CM}_\forall $
, this is proved just like the soundness theorem for the usual semantics of first-order logic.□
$\mathsf {CM}_\forall $
, this is proved just like the soundness theorem for the usual semantics of first-order logic.□
The theory
![]() $\mathsf {MS}$
(standing for Multiverse theory of Satisfaction) is analogous to the Friedman–Sheard theory of truth
$\mathsf {MS}$
(standing for Multiverse theory of Satisfaction) is analogous to the Friedman–Sheard theory of truth
![]() $\mathsf {FS}$
:
$\mathsf {FS}$
:
System 4.5 (
 $\mathsf {MS}$
)
$\mathsf {MS}$
)
Consider these rules of proof:
The system
![]() $\mathsf {MS}^-$
is
$\mathsf {MS}^-$
is
![]() $\mathsf {CM}^- + \mathsf {NEC} + \mathsf {CONEC}$
and the system
$\mathsf {CM}^- + \mathsf {NEC} + \mathsf {CONEC}$
and the system
![]() $\mathsf {MS}$
is
$\mathsf {MS}$
is
![]() $\mathsf {CM} + \mathsf {NEC} + \mathsf {CONEC}$
.
$\mathsf {CM} + \mathsf {NEC} + \mathsf {CONEC}$
.
If
![]() $\mathcal {L}^{\prime }$
expands
$\mathcal {L}^{\prime }$
expands
![]() $\mathcal {L}$
, then we write
$\mathcal {L}$
, then we write
![]() $\mathsf {MS}^-(\mathcal {L}^{\prime })$
and
$\mathsf {MS}^-(\mathcal {L}^{\prime })$
and
![]() $\mathsf {MS}(\mathcal {L}^{\prime })$
for the corresponding systems obtained by replacing all occurrences of
$\mathsf {MS}(\mathcal {L}^{\prime })$
for the corresponding systems obtained by replacing all occurrences of
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
, in the axioms of the form
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
, in the axioms of the form
![]() $\mathsf {CM}_-$
and in the rules
$\mathsf {CM}_-$
and in the rules
![]() $\mathsf {NEC}, \mathsf {CONEC}$
, by the language
$\mathsf {NEC}, \mathsf {CONEC}$
, by the language
![]() $\mathcal {L}^{\prime }_{\mathsf {Uni}, \mathsf {Mod}}$
.
$\mathcal {L}^{\prime }_{\mathsf {Uni}, \mathsf {Mod}}$
.
Recall that if S is a system involving deductive rules, and A is an axiom, then
![]() $S + A$
denotes the natural extension of S in which these deductive rules may be applied to proofs also involving A. For example, in
$S + A$
denotes the natural extension of S in which these deductive rules may be applied to proofs also involving A. For example, in
![]() $\mathsf {MS} + \exists x \hspace {2pt} \mathsf {Uni}(x)$
we may use
$\mathsf {MS} + \exists x \hspace {2pt} \mathsf {Uni}(x)$
we may use
![]() $\mathsf {NEC}$
to derive
$\mathsf {NEC}$
to derive
![]() $\forall \mathcal {U} \in \mathsf {Uni} \hspace {2pt} \mathsf {Mod}(\mathcal {U}, \ulcorner \exists x \hspace {2pt} \mathsf {Uni}(x) \urcorner )$
.
$\forall \mathcal {U} \in \mathsf {Uni} \hspace {2pt} \mathsf {Mod}(\mathcal {U}, \ulcorner \exists x \hspace {2pt} \mathsf {Uni}(x) \urcorner )$
.
Figure 2 displays reflective axioms, modal axioms and the system
![]() $\mathsf {GL}_{\mathsf {CM}^-}$
interpreting Gödel–Löb logic.
$\mathsf {GL}_{\mathsf {CM}^-}$
interpreting Gödel–Löb logic.

Fig. 2 Semantically motivated multiverse axioms.
The reflective axioms may be viewed as statements, of increasing strength, that the universe of the background theory is reflected in the multiverse: Non-Triviality just says that there is a universe in the multiverse;
![]() $\textsf {Multiverse Reflection}$
is equivalent to that any
$\textsf {Multiverse Reflection}$
is equivalent to that any
![]() $\mathcal {L}$
-sentence holding in the background universe also holds in some universe; and
$\mathcal {L}$
-sentence holding in the background universe also holds in some universe; and
![]() $\textsf {Self-Perception}$
goes as far as saying that the background universe is isomorphic to a universe in the multiverse.
$\textsf {Self-Perception}$
goes as far as saying that the background universe is isomorphic to a universe in the multiverse.
The next theorem applies standard arguments from axiomatic theories of truth to exhibit semantically motivated axioms that turn out to be paradoxical.
Theorem 4.6.
-
(a) The following axiom schema is inconsistent over
 $\mathsf {CM}^- + \mathsf {NEC}$
:
$\mathsf {CM}^- + \mathsf {NEC}$
:  $$ \begin{align*} \begin{array}{ll} \mathsf{T}_{\mathsf{CM}} & \forall \sigma \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}), \hspace{2pt} \mathsf{Tr}^\Box(\ulcorner \sigma \urcorner) \rightarrow \sigma. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathsf{T}_{\mathsf{CM}} & \forall \sigma \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}), \hspace{2pt} \mathsf{Tr}^\Box(\ulcorner \sigma \urcorner) \rightarrow \sigma. \end{array} \end{align*} $$
-
(b) The following axiom schema is inconsistent over
 $\mathsf {CM}^- + \mathsf {NEC} + \textsf {Non-Triviality}$
:
$\mathsf {CM}^- + \mathsf {NEC} + \textsf {Non-Triviality}$
:  $$ \begin{align*} \begin{array}{ll} \mathsf{4}_{\mathsf{CM}} & \forall \sigma \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}), \hspace{2pt} \mathsf{Tr}^\Box(\ulcorner \sigma \urcorner) \rightarrow \mathsf{Tr}^\Box(\ulcorner \mathsf{Tr}^\Box(\ulcorner \sigma \urcorner) \urcorner). \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \mathsf{4}_{\mathsf{CM}} & \forall \sigma \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}), \hspace{2pt} \mathsf{Tr}^\Box(\ulcorner \sigma \urcorner) \rightarrow \mathsf{Tr}^\Box(\ulcorner \mathsf{Tr}^\Box(\ulcorner \sigma \urcorner) \urcorner). \\ \end{array} \end{align*} $$
Remark. Note that
![]() $\mathsf {T}_{\mathsf {CM}}$
is the untyped version of Multiverse Reflection.
$\mathsf {T}_{\mathsf {CM}}$
is the untyped version of Multiverse Reflection.
Proof. By Gödel diagonalization, there is an
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-sentence
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-sentence
![]() $\lambda $
, such that
$\lambda $
, such that
By
![]() $\mathsf {T}_{\mathsf {CM}}$
,
$\mathsf {T}_{\mathsf {CM}}$
,
![]() $\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \rightarrow \lambda $
, so we get
$\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \rightarrow \lambda $
, so we get
![]() $\neg \mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
, and therefore
$\neg \mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
, and therefore
![]() $\lambda $
. Now
$\lambda $
. Now
![]() $\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
follows by
$\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
follows by
![]() $\mathsf {NEC}$
, a contradiction.
$\mathsf {NEC}$
, a contradiction.
By
![]() $\mathsf {4}_{\mathsf {CM}}$
,
$\mathsf {4}_{\mathsf {CM}}$
,
![]() $\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \rightarrow \mathsf {Tr}^\Box (\ulcorner \mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \urcorner )$
, so by
$\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \rightarrow \mathsf {Tr}^\Box (\ulcorner \mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \urcorner )$
, so by
![]() $\mathsf {CM}^\Box _\leftrightarrow $
,
$\mathsf {CM}^\Box _\leftrightarrow $
,
![]() $\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \rightarrow \mathsf {Tr}^\Box (\ulcorner \neg \lambda \urcorner )$
, and by
$\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \rightarrow \mathsf {Tr}^\Box (\ulcorner \neg \lambda \urcorner )$
, and by
![]() $\mathsf {CM}^\Box _\neg $
(using Non-Triviality),
$\mathsf {CM}^\Box _\neg $
(using Non-Triviality),
![]() $\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \rightarrow \neg \mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
. So we get
$\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner ) \rightarrow \neg \mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
. So we get
![]() $\neg \mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
and therefore
$\neg \mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
and therefore
![]() $\lambda $
. Now
$\lambda $
. Now
![]() $\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
follows by
$\mathsf {Tr}^\Box (\ulcorner \lambda \urcorner )$
follows by
![]() $\mathsf {NEC}$
, a contradiction.□
$\mathsf {NEC}$
, a contradiction.□
The following proposition relates the natural systems obtained by adding reflective axioms to
![]() ${\mathsf {CM}^-} + \mathsf {NEC}$
.
${\mathsf {CM}^-} + \mathsf {NEC}$
.
Proposition 4.7. Over
![]() ${\mathsf {CM}^-} + \mathsf {NEC}$
:
${\mathsf {CM}^-} + \mathsf {NEC}$
:
-
(a)
 $\textsf {Multiverse Reflection} \vdash \textsf {Non-Triviality}$
.
$\textsf {Multiverse Reflection} \vdash \textsf {Non-Triviality}$
. -
(b)
 $\textsf {Self-Perception} \vdash \textsf {Multiverse Reflection}$
.
$\textsf {Self-Perception} \vdash \textsf {Multiverse Reflection}$
.
Proof.
-
(a) From
 $\mathsf {Tr}^\Box (\ulcorner \bot \urcorner ) \rightarrow \bot $
we get
$\mathsf {Tr}^\Box (\ulcorner \bot \urcorner ) \rightarrow \bot $
we get
 $\neg \forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} \mathsf {Mod}(\mathcal {U}, \ulcorner \bot \urcorner )$
, whence Non-Triviality.
$\neg \forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} \mathsf {Mod}(\mathcal {U}, \ulcorner \bot \urcorner )$
, whence Non-Triviality. -
(b) Let
 $\sigma \in \mathcal {L}$
, and assume
$\sigma \in \mathcal {L}$
, and assume
 $\mathsf {Tr}^\Box (\ulcorner \sigma \urcorner )$
. Then
$\mathsf {Tr}^\Box (\ulcorner \sigma \urcorner )$
. Then
 $\mathsf {Mod}(\mathsf {self}, \ulcorner \sigma \urcorner )$
. So by Proposition 2.16, we have
$\mathsf {Mod}(\mathsf {self}, \ulcorner \sigma \urcorner )$
. So by Proposition 2.16, we have
 $\sigma $
.
$\sigma $
.
□
![]() $\mathsf {Comp}_{\mathsf {CM}}$
in Figure 2 includes two axioms that refer to the theory
$\mathsf {Comp}_{\mathsf {CM}}$
in Figure 2 includes two axioms that refer to the theory
![]() $\mathsf {Comp}_{\mathsf {CM}}$
. These axioms can be constructed by Gödel’s fixed-point lemma. The following theorem shows that
$\mathsf {Comp}_{\mathsf {CM}}$
. These axioms can be constructed by Gödel’s fixed-point lemma. The following theorem shows that
![]() $(\Box \mapsto \mathsf {Tr}^\Box )$
generates an interpretation of Gödel–Löb provability logic in
$(\Box \mapsto \mathsf {Tr}^\Box )$
generates an interpretation of Gödel–Löb provability logic in
![]() $\mathsf {Comp}_{\mathsf {CM}}$
, which in turn is interpretable in
$\mathsf {Comp}_{\mathsf {CM}}$
, which in turn is interpretable in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Theorem 4.8.
-
(a) There is an interpretation
 $\mathcal {B}$
of the system
$\mathcal {B}$
of the system
 $\mathsf {K}$
of modal propositional logicFootnote
11
in
$\mathsf {K}$
of modal propositional logicFootnote
11
in
 $\mathsf {CM}^- + \mathsf {NEC}$
, satisfying any given assignment of the propositional variables, and
$\mathsf {CM}^- + \mathsf {NEC}$
, satisfying any given assignment of the propositional variables, and  $$ \begin{align*} &\mathcal{B}(\Box \sigma) = \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathcal{B}}(\ulcorner \sigma \urcorner)) \text{, for each modal propositional formula } \sigma. \end{align*} $$
$$ \begin{align*} &\mathcal{B}(\Box \sigma) = \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathcal{B}}(\ulcorner \sigma \urcorner)) \text{, for each modal propositional formula } \sigma. \end{align*} $$
-
(b)
 $\mathcal {B}$
above interprets the system
$\mathcal {B}$
above interprets the system
 $\mathsf {GL}$
of modal predicate logicFootnote
12
in
$\mathsf {GL}$
of modal predicate logicFootnote
12
in
 $\mathsf {Comp}_{\mathsf {CM}}$
. In particular,
$\mathsf {Comp}_{\mathsf {CM}}$
. In particular,  $$ \begin{align*} \mathsf{Comp}_{\mathsf{CM}} \vdash \mathsf{K}_{\mathsf{CM}} + \mathsf{4}_{\mathsf{CM}} + \textsf{L}\ddot{\textsf{o}}\textsf{b}_{\mathsf{CM}} + \mathsf{NEC}. \end{align*} $$
$$ \begin{align*} \mathsf{Comp}_{\mathsf{CM}} \vdash \mathsf{K}_{\mathsf{CM}} + \mathsf{4}_{\mathsf{CM}} + \textsf{L}\ddot{\textsf{o}}\textsf{b}_{\mathsf{CM}} + \mathsf{NEC}. \end{align*} $$
-
(c)
 $\mathsf {ZF}$
interprets
$\mathsf {ZF}$
interprets
 $\mathsf {Comp}_{\mathsf {CM}}$
. If
$\mathsf {Comp}_{\mathsf {CM}}$
. If
 $\mathsf {ZF}$
is closed under the Reflection rule (or if
$\mathsf {ZF}$
is closed under the Reflection rule (or if
 $\mathsf {ZF}$
is
$\mathsf {ZF}$
is
 $\omega $
-consistent), then
$\omega $
-consistent), then
 $\mathsf {ZF}$
interprets
$\mathsf {ZF}$
interprets
 $\mathsf {Comp}_{\mathsf {CM}} + \mathsf {CONEC}$
.
$\mathsf {Comp}_{\mathsf {CM}} + \mathsf {CONEC}$
.
Proof.
-
(a) The interpretation
 $\mathcal {B}$
can be constructed by primitive recursion, using the technique described in [Reference Halbach11, chap. Reference Friedman and Sheard5.Reference Enayat3]. By
$\mathcal {B}$
can be constructed by primitive recursion, using the technique described in [Reference Halbach11, chap. Reference Friedman and Sheard5.Reference Enayat3]. By
 $\mathsf {NEC}$
,
$\mathsf {NEC}$
,
 $\mathcal {B}$
validates the modal necessitation rule, and by
$\mathcal {B}$
validates the modal necessitation rule, and by
 $\mathsf {CM}^\Box _\rightarrow $
(from which
$\mathsf {CM}^\Box _\rightarrow $
(from which
 $\mathsf {K}_{\mathsf {CM}}$
is easily derived), it validates K.
$\mathsf {K}_{\mathsf {CM}}$
is easily derived), it validates K. -
(b) By the Soundness Lemma,
(*)We apply the Hilbert–Bernays–Löb provability conditions. For $$ \begin{align} \mathsf{Comp}_{\mathsf{CM}} \vdash \forall \sigma \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} (\Pr{}_{\mathsf{GL}_{\mathsf{CM}}}(\sigma) \leftrightarrow \mathsf{Tr}^\Box(\sigma)). \end{align} $$
$$ \begin{align} \mathsf{Comp}_{\mathsf{CM}} \vdash \forall \sigma \in \mathrm{Sent}(\mathcal{L}_{\mathsf{Uni}, \mathsf{Mod}}) \hspace{2pt} (\Pr{}_{\mathsf{GL}_{\mathsf{CM}}}(\sigma) \leftrightarrow \mathsf{Tr}^\Box(\sigma)). \end{align} $$
 $\mathsf {NEC}$
, note that for each
$\mathsf {NEC}$
, note that for each
 $\sigma \in \mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
,
$\sigma \in \mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
,
 $\mathsf {Comp}_{\mathsf {CM}} \vdash \sigma \Rightarrow \mathsf {Comp}_{\mathsf {CM}} \vdash \Pr _{\mathsf {Comp}_{\mathsf {CM}}}(\ulcorner \sigma \urcorner )$
, and apply (*). For
$\mathsf {Comp}_{\mathsf {CM}} \vdash \sigma \Rightarrow \mathsf {Comp}_{\mathsf {CM}} \vdash \Pr _{\mathsf {Comp}_{\mathsf {CM}}}(\ulcorner \sigma \urcorner )$
, and apply (*). For
 $\mathsf {4}_{\mathsf {CM}}$
, note that for each
$\mathsf {4}_{\mathsf {CM}}$
, note that for each
 $\sigma \in \mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
,
$\sigma \in \mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
,
 $\mathsf {Comp}_{\mathsf {CM}} \vdash \Pr _{\mathsf {Comp}_{\mathsf {CM}}}(\ulcorner \sigma \urcorner ) \rightarrow \Pr _{\mathsf {Comp}_{\mathsf {CM}}}(\ulcorner \Pr _{\mathsf {Comp}_{\mathsf {CM}}}(\ulcorner \sigma \urcorner ) \urcorner )$
, and apply (*) both externally and internally. By Löb’s Theorem (see Lemma 13.7 in [Reference Halbach11]) and the preceding item, we are done.
$\mathsf {Comp}_{\mathsf {CM}} \vdash \Pr _{\mathsf {Comp}_{\mathsf {CM}}}(\ulcorner \sigma \urcorner ) \rightarrow \Pr _{\mathsf {Comp}_{\mathsf {CM}}}(\ulcorner \Pr _{\mathsf {Comp}_{\mathsf {CM}}}(\ulcorner \sigma \urcorner ) \urcorner )$
, and apply (*) both externally and internally. By Löb’s Theorem (see Lemma 13.7 in [Reference Halbach11]) and the preceding item, we are done.
-
(c) Let
 $\mathcal {C}$
be the interpretation generated by: By the Tarskian conditions of satisfaction,
$\mathcal {C}$
be the interpretation generated by: By the Tarskian conditions of satisfaction, $$ \begin{align*} \mathsf{Uni}(\mathcal{U}) &\mapsto \mathcal{U} \models \mathsf{Comp}_{\mathsf{CM}}, \\ \mathsf{Mod}(\mathsf{Uni}, \phi, f) &\mapsto \mathcal{U} \models (\phi, f). \end{align*} $$
$$ \begin{align*} \mathsf{Uni}(\mathcal{U}) &\mapsto \mathcal{U} \models \mathsf{Comp}_{\mathsf{CM}}, \\ \mathsf{Mod}(\mathsf{Uni}, \phi, f) &\mapsto \mathcal{U} \models (\phi, f). \end{align*} $$
 $\mathsf {ZF} \vdash \mathcal {C}(\mathsf {CM}^-)$
. By construction of
$\mathsf {ZF} \vdash \mathcal {C}(\mathsf {CM}^-)$
. By construction of
 $\mathcal {C}$
,
$\mathcal {C}$
,
 $\mathsf {ZF} \vdash \mathcal {C}(\mathsf {Multiverse}_{\mathsf {Comp}_{\mathsf {CM}}}).$
By construction of
$\mathsf {ZF} \vdash \mathcal {C}(\mathsf {Multiverse}_{\mathsf {Comp}_{\mathsf {CM}}}).$
By construction of
 $\mathcal {C}$
and the Completeness theorem,
$\mathcal {C}$
and the Completeness theorem,
 $\mathsf {ZF} \vdash \mathcal {C}(\mathsf {Completeness}_{\mathsf {Comp}_{\mathsf {CM}}}).$
From (*), it is easily seen that the Reflection rule yields
$\mathsf {ZF} \vdash \mathcal {C}(\mathsf {Completeness}_{\mathsf {Comp}_{\mathsf {CM}}}).$
From (*), it is easily seen that the Reflection rule yields
 $\mathsf {CONEC}$
. By Proposition 2.11,
$\mathsf {CONEC}$
. By Proposition 2.11,
 $\omega $
-consistency suffices.□
$\omega $
-consistency suffices.□
5 Interpreting the Copernican multiverse of sets
Now we proceed to lay forth a technique for validating the theories in Section 4 by means of the revision-semantic construction in Section 3. The Main Lemma establishes that a variety of Copernican multiverse theories can by interpreted in a suitable hierarchy of theories.
First we need a lemma establishing a normal form for derivation in
![]() $\mathsf {MS}$
. The analogous result for the case of the Friedman–Sheard theory of truth (over arithmetic) was established by [Reference Broberg1]. The authors are grateful to Broberg for allowing the inclusion of his proof re-worked for the system
$\mathsf {MS}$
. The analogous result for the case of the Friedman–Sheard theory of truth (over arithmetic) was established by [Reference Broberg1]. The authors are grateful to Broberg for allowing the inclusion of his proof re-worked for the system
![]() $\mathsf {MS}$
. We write
$\mathsf {MS}$
. We write
![]() $\mathsf {MS}^-_{\mathrm {NC}} + S$
for the system whose theorems are the conclusions of Hilbert-style proofs in
$\mathsf {MS}^-_{\mathrm {NC}} + S$
for the system whose theorems are the conclusions of Hilbert-style proofs in
![]() $\mathsf {MS}^- + S$
such that all applications of
$\mathsf {MS}^- + S$
such that all applications of
![]() $\mathsf {NEC}$
are before all applications of
$\mathsf {NEC}$
are before all applications of
![]() $\mathsf {CONEC}$
.
$\mathsf {CONEC}$
.
Lemma 5.1. Let S be a theory. If
![]() $\mathsf {MS}^- + S \vdash \psi $
, then there exists
$\mathsf {MS}^- + S \vdash \psi $
, then there exists
![]() $\chi $
such that
$\chi $
such that
![]() $\mathsf {CM}^- + \mathsf {NEC} + S \vdash \chi $
and
$\mathsf {CM}^- + \mathsf {NEC} + S \vdash \chi $
and
![]() $\mathsf {CM}^- + \mathsf {CONEC} + S + \chi \vdash \psi $
.
$\mathsf {CM}^- + \mathsf {CONEC} + S + \chi \vdash \psi $
.
Proof. For simplicity, we assume that all formulas in all theories and proofs considered are sentences; there is an adequate Hilbert-style proof system meeting this assumption. It suffices to show that
![]() $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi $
.
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi $
.
Let
![]() $\rho $
be a Hilbert-style proof, with
$\rho $
be a Hilbert-style proof, with
![]() $\psi _0, \ldots , \psi _{l-1}$
as rows, of
$\psi _0, \ldots , \psi _{l-1}$
as rows, of
![]() $\psi _{l-1}$
in
$\psi _{l-1}$
in
![]() $\mathsf {MS}^- + S$
. By induction, we may assume that
$\mathsf {MS}^- + S$
. By induction, we may assume that
![]() $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi _r$
, for each
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi _r$
, for each
![]() $r < l-1$
. There are four cases to consider as to how the last row of
$r < l-1$
. There are four cases to consider as to how the last row of
![]() $\rho $
is obtained:
$\rho $
is obtained:
-
(Axiom)
 $\psi _{l-1}$
is an axiom.
$\psi _{l-1}$
is an axiom. -
(First-order)
 $\psi _{l-1}$
is derived by a rule of inference of first-order logic.
$\psi _{l-1}$
is derived by a rule of inference of first-order logic. -
(CONEC)
 $\psi _{l-1}$
is derived from
$\psi _{l-1}$
is derived from
 $\psi _{r}$
by
$\psi _{r}$
by
 $\mathsf {CONEC}$
, for some
$\mathsf {CONEC}$
, for some
 $r < l-1$
.
$r < l-1$
. -
(NEC)
 $\psi _{l-1}$
is derived from
$\psi _{l-1}$
is derived from
 $\psi _{r}$
by
$\psi _{r}$
by
 $\mathsf {NEC}$
, for some
$\mathsf {NEC}$
, for some
 $r < l-1$
.
$r < l-1$
.
We proceed to establish
![]() $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi _{l-1}$
for each case.
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi _{l-1}$
for each case.
-
(Axiom) In this case
 $\psi _{l-1}$
is also an axiom of
$\psi _{l-1}$
is also an axiom of
 $\mathsf {MS}^-_{\mathrm {NC}} + S$
(a proof of length
$\mathsf {MS}^-_{\mathrm {NC}} + S$
(a proof of length
 $1$
).
$1$
). -
(First-order) In this case
 $\psi _{l-1}$
is also derived by the same rule in
$\psi _{l-1}$
is also derived by the same rule in
 $\mathsf {MS}^-_{\mathrm {NC}} + S$
, utilizing the induction hypothesis.
$\mathsf {MS}^-_{\mathrm {NC}} + S$
, utilizing the induction hypothesis. -
(CONEC) In this case
 $\psi _{l-1}$
is also derived by
$\psi _{l-1}$
is also derived by
 $\mathsf {CONEC}$
in
$\mathsf {CONEC}$
in
 $\mathsf {MS}^-_{\mathrm {NC}} + S$
, utilizing the induction hypothesis and that this application of
$\mathsf {MS}^-_{\mathrm {NC}} + S$
, utilizing the induction hypothesis and that this application of
 $\mathsf {CONEC}$
is right at the end, after all applications of
$\mathsf {CONEC}$
is right at the end, after all applications of
 $\mathsf {NEC}$
.
$\mathsf {NEC}$
. -
(NEC) This is the case requiring work. We have that
 $\psi _{l-1}$
is the sentence
$\psi _{l-1}$
is the sentence
 $\mathsf {Tr}^\Box (\ulcorner \psi _r \urcorner )$
and that
$\mathsf {Tr}^\Box (\ulcorner \psi _r \urcorner )$
and that
 $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi _r$
. Let
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi _r$
. Let
 $\theta _0, \ldots , \theta _{k-1} = \psi _r$
be the rows of a Hilbert-style proof
$\theta _0, \ldots , \theta _{k-1} = \psi _r$
be the rows of a Hilbert-style proof
 $\pi $
witnessing this. We proceed to show
$\pi $
witnessing this. We proceed to show
 $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \mathsf {Tr}^\Box (\ulcorner \theta _q \urcorner )$
, for each
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \mathsf {Tr}^\Box (\ulcorner \theta _q \urcorner )$
, for each
 $q \leq k-1$
. By induction, we may assume that this holds for each
$q \leq k-1$
. By induction, we may assume that this holds for each
 $q < k-1$
. Again there are four cases to consider as to how the last row of
$q < k-1$
. Again there are four cases to consider as to how the last row of
 $\pi $
is obtained:
$\pi $
is obtained:-
(Axiom’)
 $\theta _{k-1}$
is an axiom.
$\theta _{k-1}$
is an axiom. -
(First-order’)
 $\theta _{k-1}$
is derived by a rule of inference of first-order logic.
$\theta _{k-1}$
is derived by a rule of inference of first-order logic. -
(CONEC’)
 $\theta _{k-1}$
is derived from
$\theta _{k-1}$
is derived from
 $\theta _{q}$
by
$\theta _{q}$
by
 $\mathsf {CONEC}$
, for some
$\mathsf {CONEC}$
, for some
 $q < k-1$
.
$q < k-1$
. -
(NEC’)
 $\theta _{k-1}$
is derived from
$\theta _{k-1}$
is derived from
 $\theta _{q}$
by
$\theta _{q}$
by
 $\mathsf {NEC}$
, for some
$\mathsf {NEC}$
, for some
 $q < k-1$
.
$q < k-1$
.
 $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
for each case.
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
for each case.-
(Axiom’) In this case we apply
 $\mathsf {NEC}$
to
$\mathsf {NEC}$
to
 $\theta _{k-1}$
to obtain a proof of
$\theta _{k-1}$
to obtain a proof of
 $\mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
(of length
$\mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
(of length
 $2$
).
$2$
). -
(First-order’) We have
 $q_0 < \cdots < q_n < k-1$
, such that
$q_0 < \cdots < q_n < k-1$
, such that
 $\{\theta _{q_0}, \ldots , \theta _{q_n}\} \vdash \theta _{k-1}$
. By the induction hypothesis,
$\{\theta _{q_0}, \ldots , \theta _{q_n}\} \vdash \theta _{k-1}$
. By the induction hypothesis,
 $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \mathsf {Tr}^\Box (\ulcorner \theta _{q_i} \urcorner )$
, for each
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \mathsf {Tr}^\Box (\ulcorner \theta _{q_i} \urcorner )$
, for each
 $0 \leq i \leq n$
. Clearly, these proofs can be merged (respecting the requirement on the order of the applications of
$0 \leq i \leq n$
. Clearly, these proofs can be merged (respecting the requirement on the order of the applications of
 $\mathsf {NEC}$
and
$\mathsf {NEC}$
and
 $\mathsf {CONEC}$
) into one Hilbert-style proof in
$\mathsf {CONEC}$
) into one Hilbert-style proof in
 $\mathsf {MS}^-_{\mathrm {NC}} + S$
in which
$\mathsf {MS}^-_{\mathrm {NC}} + S$
in which
 $\mathsf {Tr}^\Box (\ulcorner \theta _{q_0} \urcorner ), \ldots , \mathsf {Tr}^\Box (\ulcorner \theta _{q_n} \urcorner )$
are derived.Now note that by the Soundness Lemma, We add a proof of that (which has no applications of
$\mathsf {Tr}^\Box (\ulcorner \theta _{q_0} \urcorner ), \ldots , \mathsf {Tr}^\Box (\ulcorner \theta _{q_n} \urcorner )$
are derived.Now note that by the Soundness Lemma, We add a proof of that (which has no applications of $$ \begin{align*}\mathsf{CM}^- + \{\mathsf{Tr}^\Box(\ulcorner \theta_{q_0} \urcorner), \ldots, \mathsf{Tr}^\Box(\ulcorner \theta_{q_n} \urcorner)\} \vdash \mathsf{Tr}^\Box(\ulcorner \theta_{k-1} \urcorner).\end{align*} $$
$$ \begin{align*}\mathsf{CM}^- + \{\mathsf{Tr}^\Box(\ulcorner \theta_{q_0} \urcorner), \ldots, \mathsf{Tr}^\Box(\ulcorner \theta_{q_n} \urcorner)\} \vdash \mathsf{Tr}^\Box(\ulcorner \theta_{k-1} \urcorner).\end{align*} $$
 $\mathsf {NEC}$
or
$\mathsf {NEC}$
or
 $\mathsf {CONEC}$
) to the end of the previous proof, obtaining
$\mathsf {CONEC}$
) to the end of the previous proof, obtaining
 $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
, as desired.
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
, as desired.
-
(CONEC’) In this case
 $\mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
equals
$\mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
equals
 $\theta _q$
, which we already have a proof of.
$\theta _q$
, which we already have a proof of. -
(NEC’) In this case the last step of
 $\pi $
is obtained by
$\pi $
is obtained by
 $\mathsf {NEC}$
, so there cannot be any application of
$\mathsf {NEC}$
, so there cannot be any application of
 $\mathsf {CONEC}$
in
$\mathsf {CONEC}$
in
 $\pi $
. Hence, we can make an extra application of
$\pi $
. Hence, we can make an extra application of
 $\mathsf {NEC}$
at the end of
$\mathsf {NEC}$
at the end of
 $\pi $
to obtain a proof of
$\pi $
to obtain a proof of
 $\mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
in
$\mathsf {Tr}^\Box (\ulcorner \theta _{k-1} \urcorner )$
in
 $\mathsf {MS}^-_{\mathrm {NC}} + S$
.
$\mathsf {MS}^-_{\mathrm {NC}} + S$
.
-
□
Before embarking on proving the Main Lemma of the paper, we introduce notation for the kind of interpretations involved. The Main Lemma encapsulates the revision-semantic construction of a model of “the Copernican multiverse of sets.”
Let
![]() $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
be revision parameters. Let S be a set theory in a language L and let t be an L-term such that
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
be revision parameters. Let S be a set theory in a language L and let t be an L-term such that
![]() $S \vdash t \in \mathbb {N}$
. Then
$S \vdash t \in \mathbb {N}$
. Then
![]() $\mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{L, t}$
denotes the interpretation of the language
$\mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{L, t}$
denotes the interpretation of the language
![]() $L_{\mathsf {Uni}, \mathsf {Mod}}$
into L generated by interpreting
$L_{\mathsf {Uni}, \mathsf {Mod}}$
into L generated by interpreting
![]() $\mathsf {Mod}$
as
$\mathsf {Mod}$
as
![]() $\mathrm {Mod}_t$
(obtained from Construction 3.2) and
$\mathrm {Mod}_t$
(obtained from Construction 3.2) and
![]() $\mathsf {Uni}$
as
$\mathsf {Uni}$
as
![]() $\mathrm {Uni}_t$
. (Although the full notation is
$\mathrm {Uni}_t$
. (Although the full notation is
![]() $\mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{L, t}$
, with
$\mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{L, t}$
, with
![]() $L, \mathsf {Uni}, \mathsf {Mod}$
fixed, for example, we denote this interpretation by
$L, \mathsf {Uni}, \mathsf {Mod}$
fixed, for example, we denote this interpretation by
![]() $\mathcal {I}_t$
.) Note that this interpretation fixes each formula in L.
$\mathcal {I}_t$
.) Note that this interpretation fixes each formula in L.
More generally, if
![]() $\mathcal {S} \vdash \exists ^! x \hspace {2pt} (\phi (x) \wedge x \in \mathbb {N})$
, then
$\mathcal {S} \vdash \exists ^! x \hspace {2pt} (\phi (x) \wedge x \in \mathbb {N})$
, then
![]() $\mathcal {I}_\phi $
denotes the interpretation generated by interpreting
$\mathcal {I}_\phi $
denotes the interpretation generated by interpreting
![]() $\mathsf {Mod}$
by
$\mathsf {Mod}$
by
![]() $\forall x \in \mathbb {N} \hspace {2pt} (\phi (x) \rightarrow \mathrm {Mod}_x)$
and
$\forall x \in \mathbb {N} \hspace {2pt} (\phi (x) \rightarrow \mathrm {Mod}_x)$
and
![]() $\mathsf {Uni}$
by
$\mathsf {Uni}$
by
![]() $\forall x \in \mathbb {N} \hspace {2pt} (\phi (x) \rightarrow \mathrm {Uni}_x)$
. We may expand the language with a constant symbol
$\forall x \in \mathbb {N} \hspace {2pt} (\phi (x) \rightarrow \mathrm {Uni}_x)$
. We may expand the language with a constant symbol
![]() $c_\phi $
and extend
$c_\phi $
and extend
![]() $\mathcal {S}$
with the axiom
$\mathcal {S}$
with the axiom
![]() $\forall x \hspace {2pt} (\phi (x) \leftrightarrow x = c_\phi )$
, to produce an interpretation
$\forall x \hspace {2pt} (\phi (x) \leftrightarrow x = c_\phi )$
, to produce an interpretation
![]() $\mathcal {I}_{c_\phi }$
equivalent to
$\mathcal {I}_{c_\phi }$
equivalent to
![]() $\mathcal {I}_\phi $
.
$\mathcal {I}_\phi $
.
Let
![]() $T_0$
and
$T_0$
and
![]() $T_1$
be theories in the languages
$T_1$
be theories in the languages
![]() $L_0$
and
$L_0$
and
![]() $L_1$
, respectively. Let
$L_1$
, respectively. Let
![]() $\mathfrak {F}$
be a family (set) of interpretations from
$\mathfrak {F}$
be a family (set) of interpretations from
![]() $L_0$
to
$L_0$
to
![]() $L_1$
. We say that
$L_1$
. We say that
![]() $\mathfrak {F}$
is a local interpretation of
$\mathfrak {F}$
is a local interpretation of
![]() $T_0$
in
$T_0$
in
![]() $T_1$
if for any finite set
$T_1$
if for any finite set
![]() $T^{\prime }_0$
of consequences of
$T^{\prime }_0$
of consequences of
![]() $T_0$
, there is an
$T_0$
, there is an
![]() $\mathcal {I} \in \mathfrak {F}$
which interprets
$\mathcal {I} \in \mathfrak {F}$
which interprets
![]() $T^{\prime }_0$
in
$T^{\prime }_0$
in
![]() $T_1$
. Alternatively, we say that
$T_1$
. Alternatively, we say that
![]() $T_1$
locally interprets
$T_1$
locally interprets
![]() $T_0$
by
$T_0$
by
![]() $\mathfrak {F}$
, respectively.
$\mathfrak {F}$
, respectively.
Given revision parameters
![]() $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
, recall that
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
, recall that
![]() $\mathcal {L}^{\mathrm {T}}$
is the language of the theories
$\mathcal {L}^{\mathrm {T}}$
is the language of the theories
![]() $\mathbf {T}_n$
and that
$\mathbf {T}_n$
and that
![]() $\mathcal {L}^{\mathrm {Rev}}$
is any sublanguage of
$\mathcal {L}^{\mathrm {Rev}}$
is any sublanguage of
![]() $\mathcal {L}^{\mathrm {T}}$
.
$\mathcal {L}^{\mathrm {T}}$
.
Main Lemma. Let
![]() $\mathrm {T}$
,
$\mathrm {T}$
,
![]() $\mathrm {Uni}$
and
$\mathrm {Uni}$
and
![]() $\mathrm {Mod}_0$
be revision parameters such that
$\mathrm {Mod}_0$
be revision parameters such that
![]() $\mathbf {T}_\omega \vdash \mathsf {ZF}$
, let
$\mathbf {T}_\omega \vdash \mathsf {ZF}$
, let
![]() $\mathfrak {F} = \{\mathcal {I}_{\underline {k}} \mid k \in \mathbb {N}\}$
and let S be an
$\mathfrak {F} = \{\mathcal {I}_{\underline {k}} \mid k \in \mathbb {N}\}$
and let S be an
![]() $\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
-theory such that for any finite
$\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
-theory such that for any finite
![]() $\Gamma \subseteq S$
,
$\Gamma \subseteq S$
,
-
(a) If
 $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
 $\mathsf {NEC}^*$
, then
$\mathsf {NEC}^*$
, then
 $\mathbf {T}_\omega $
locally interprets
$\mathbf {T}_\omega $
locally interprets
 $\mathsf {CM}^- + \mathsf {NEC} + S$
by
$\mathsf {CM}^- + \mathsf {NEC} + S$
by
 $\mathfrak {F}$
.
$\mathfrak {F}$
. -
(b) If
 $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
 $\mathsf {CONEC}^*$
, then
$\mathsf {CONEC}^*$
, then
 $\mathbf {T}_\omega $
locally interprets
$\mathbf {T}_\omega $
locally interprets
 $\mathsf {CM}^- + \mathsf {CONEC} + S$
by
$\mathsf {CM}^- + \mathsf {CONEC} + S$
by
 $\mathfrak {F}$
.
$\mathfrak {F}$
. -
(c) If
 $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
 $\mathsf {NEC}^*$
and
$\mathsf {NEC}^*$
and
 $\mathsf {CONEC}^*$
, then
$\mathsf {CONEC}^*$
, then
 $\mathbf {T}_\omega $
locally interprets
$\mathbf {T}_\omega $
locally interprets
 $\mathsf {MS}^- + S$
by
$\mathsf {MS}^- + S$
by
 $\mathfrak {F}$
.
$\mathfrak {F}$
.
Proof. We prove the latter, most complicated assertion; the other two assertions follow by restricting the proof to the appropriate cases. Assume that
![]() $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
are revision parameters admitting
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
are revision parameters admitting
![]() $\mathsf {NEC}^*$
and
$\mathsf {NEC}^*$
and
![]() $\mathsf {CONEC}^*$
.
$\mathsf {CONEC}^*$
.
Assume that
![]() $\mathsf {MS}^- + S \vdash \psi $
. By Lemma 5.1, we have that
$\mathsf {MS}^- + S \vdash \psi $
. By Lemma 5.1, we have that
![]() $\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi $
. Let
$\mathsf {MS}^-_{\mathrm {NC}} + S \vdash \psi $
. Let
![]() $\rho $
be a linear Hilbert-style proof witnessing this. Let
$\rho $
be a linear Hilbert-style proof witnessing this. Let
![]() $\Gamma $
be the axioms of
$\Gamma $
be the axioms of
![]() $\mathsf {CM}^- + S$
occurring in
$\mathsf {CM}^- + S$
occurring in
![]() $\rho $
. We shall start by showing that
$\rho $
. We shall start by showing that
We have by the assumption of the lemma that there is
![]() $A < \omega $
, such that for any
$A < \omega $
, such that for any
![]() $k < \omega $
with
$k < \omega $
with
![]() $A \leq k$
, we have
$A \leq k$
, we have
![]() $\mathbf {T}_k \vdash \mathcal {I}^{\mathsf {Uni}, \mathsf {Mod}_0}_{\underline {k}}(\phi )$
, for every axiom
$\mathbf {T}_k \vdash \mathcal {I}^{\mathsf {Uni}, \mathsf {Mod}_0}_{\underline {k}}(\phi )$
, for every axiom
![]() $\phi $
of S in
$\phi $
of S in
![]() $\Gamma $
. Moreover, note that for any
$\Gamma $
. Moreover, note that for any
![]() $k < \omega $
, and any axiom
$k < \omega $
, and any axiom
![]() $\phi $
of
$\phi $
of
![]() $\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
,
$\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
,
![]() $\mathcal {I}^{\mathsf {Uni}, \mathsf {Mod}_0}_{\underline {k}}(\phi )$
is an axiom of
$\mathcal {I}^{\mathsf {Uni}, \mathsf {Mod}_0}_{\underline {k}}(\phi )$
is an axiom of
![]() $\mathsf {ZF}$
. So since
$\mathsf {ZF}$
. So since
![]() $\mathbf {T}_\omega \vdash \mathsf {ZF}$
, there is
$\mathbf {T}_\omega \vdash \mathsf {ZF}$
, there is
![]() $A' \geq 1$
with
$A' \geq 1$
with
![]() $A \leq A' < \omega $
, such that for any
$A \leq A' < \omega $
, such that for any
![]() $k < \omega $
with
$k < \omega $
with
![]() $A' \leq k$
, we have
$A' \leq k$
, we have
![]() $\mathbf {T}_{k} \vdash \mathcal {I}^{\mathsf {Uni}, \mathsf {Mod}_0}_{\underline {k}}(\phi )$
, for every axiom
$\mathbf {T}_{k} \vdash \mathcal {I}^{\mathsf {Uni}, \mathsf {Mod}_0}_{\underline {k}}(\phi )$
, for every axiom
![]() $\phi $
of
$\phi $
of
![]() $\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
in
$\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
in
![]() $\Gamma $
.
$\Gamma $
.
Suppose that
![]() $\phi $
is a compositional axiom (of the form
$\phi $
is a compositional axiom (of the form
![]() $\mathsf {CM}_-$
). Then
$\mathsf {CM}_-$
). Then
![]() $\forall A' \leq k < \omega \hspace {2pt} [\mathbf {T}_k \vdash \mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{\underline {k}}(\phi )]$
follows from that for all
$\forall A' \leq k < \omega \hspace {2pt} [\mathbf {T}_k \vdash \mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{\underline {k}}(\phi )]$
follows from that for all
![]() $\mathcal {L}^{\mathrm {T}}$
-structures
$\mathcal {L}^{\mathrm {T}}$
-structures
![]() $\mathcal {U}$
and all
$\mathcal {U}$
and all
![]() $\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
-formulas
$\mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
-formulas
![]() $\phi $
, it is provable that for all
$\phi $
, it is provable that for all
![]() $A' \leq k < \omega $
,
$A' \leq k < \omega $
,
(using
![]() $1 \leq A'$
), and from that the corresponding compositional conditions hold for
$1 \leq A'$
), and from that the corresponding compositional conditions hold for
![]() $\models $
.
$\models $
.
Hence,
![]() $A'$
satisfies (*) as desired. We introduce shifted parameters
$A'$
satisfies (*) as desired. We introduce shifted parameters
![]() $\mathrm {T}^{\prime }, \mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0$
defined by
$\mathrm {T}^{\prime }, \mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0$
defined by
![]() $\mathrm {T}^{\prime }_k \equiv _{\mathrm {df}} \mathrm {T}_{k+\underline {A'}}$
,
$\mathrm {T}^{\prime }_k \equiv _{\mathrm {df}} \mathrm {T}_{k+\underline {A'}}$
,
![]() $\mathrm {Uni}^{\prime }_k \equiv _{\mathrm {df}} \mathrm {Uni}_{k+\underline {A'}}$
and
$\mathrm {Uni}^{\prime }_k \equiv _{\mathrm {df}} \mathrm {Uni}_{k+\underline {A'}}$
and
![]() $\mathrm {Mod}^{\prime }_k \equiv _{\mathrm {df}} \mathrm {Mod}_{k+\underline {A'}}$
. Note that
$\mathrm {Mod}^{\prime }_k \equiv _{\mathrm {df}} \mathrm {Mod}_{k+\underline {A'}}$
. Note that
![]() $\mathrm {Mod}^{\prime }$
also satisfies (
$\mathrm {Mod}^{\prime }$
also satisfies (
![]() $\dagger $
) in Construction 3.2. It is easily seen that
$\dagger $
) in Construction 3.2. It is easily seen that
![]() $\mathrm {T}^{\prime }, \mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0$
are revision parameters admitting
$\mathrm {T}^{\prime }, \mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0$
are revision parameters admitting
![]() $\mathsf {NEC}^*$
and
$\mathsf {NEC}^*$
and
![]() $\mathsf {CONEC}^*$
, and that
$\mathsf {CONEC}^*$
, and that
![]() $\mathbf {T}^{\prime }_\omega = \mathbf {T}_\omega $
. Note that for all
$\mathbf {T}^{\prime }_\omega = \mathbf {T}_\omega $
. Note that for all
![]() $\phi $
, it is provable that for all
$\phi $
, it is provable that for all
![]() $k < \omega $
,
$k < \omega $
,
![]() $\mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\phi ) \leftrightarrow \mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{\underline {k+A'}}(\phi )$
.
$\mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\phi ) \leftrightarrow \mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{\underline {k+A'}}(\phi )$
.
We index the sequence of steps in the proof by numbers
![]() $0, 1, \ldots , l-1$
, where l is the length of
$0, 1, \ldots , l-1$
, where l is the length of
![]() $\rho $
. For each
$\rho $
. For each
![]() $q < l$
, let
$q < l$
, let
![]() $\psi _q$
be the derived formula (or axiom) at step q of
$\psi _q$
be the derived formula (or axiom) at step q of
![]() $\rho $
(so
$\rho $
(so
![]() $\psi = \psi _{l-1}$
), let
$\psi = \psi _{l-1}$
), let
![]() $N_q$
be the number of applications of
$N_q$
be the number of applications of
![]() $\mathsf {NEC}$
in the derivation of
$\mathsf {NEC}$
in the derivation of
![]() $\psi _q$
, and let
$\psi _q$
, and let
![]() $C_q$
be the number of applications of
$C_q$
be the number of applications of
![]() $\mathsf {CONEC}$
in the derivation of
$\mathsf {CONEC}$
in the derivation of
![]() $\psi _q$
. It suffices to show that there are natural numbers
$\psi _q$
. It suffices to show that there are natural numbers
![]() $m, n$
, such that
$m, n$
, such that
![]() $\mathbf {T}^{\prime }_m \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {n}}(\psi _q)$
, for each
$\mathbf {T}^{\prime }_m \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {n}}(\psi _q)$
, for each
![]() $q < l$
. We do so by induction on the steps of
$q < l$
. We do so by induction on the steps of
![]() $\rho $
. Let
$\rho $
. Let
![]() $r < l$
. Here is our induction hypothesis:
$r < l$
. Here is our induction hypothesis:
-
(IH)
 $\mathbf {T}^{\prime }_{2C_q + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\psi _q)$
, for any step
$\mathbf {T}^{\prime }_{2C_q + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\psi _q)$
, for any step
 $q < r$
, and for any
$q < r$
, and for any
 $k \geq N_q + 1$
.
$k \geq N_q + 1$
.
We need to show that
![]() $\mathbf {T}^{\prime }_{2C_r + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\psi _r)$
, whenever
$\mathbf {T}^{\prime }_{2C_r + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\psi _r)$
, whenever
![]() $N_r + 1 \leq k$
. There are four cases, as to which rule of inference (if any) is applied to obtain
$N_r + 1 \leq k$
. There are four cases, as to which rule of inference (if any) is applied to obtain
![]() $\psi _r$
from
$\psi _r$
from
![]() $\{\psi _q \mid q < r\}$
:
$\{\psi _q \mid q < r\}$
:
-
(Axiom)
 $\psi _r$
is an axiom in
$\psi _r$
is an axiom in
 $\Gamma $
.
$\Gamma $
. -
(First-order)
 $\psi _r$
is derived by a rule of inference of first-order logic.
$\psi _r$
is derived by a rule of inference of first-order logic. -
(NEC)
 $\psi _r$
is derived from
$\psi _r$
is derived from
 $\psi _{r'}$
by
$\psi _{r'}$
by
 $\mathsf {NEC}$
, for some
$\mathsf {NEC}$
, for some
 $r' < r$
.
$r' < r$
. -
(CONEC)
 $\psi _r$
is derived from
$\psi _r$
is derived from
 $\psi _{r'}$
by
$\psi _{r'}$
by
 $\mathsf {CONEC}$
, for some
$\mathsf {CONEC}$
, for some
 $r' < r$
.
$r' < r$
.
Let
![]() $k \geq N_r + 1$
. We proceed to show
$k \geq N_r + 1$
. We proceed to show
![]() $\mathbf {T}^{\prime }_{2C_r + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\psi _r)$
in each of the above cases. The fact that
$\mathbf {T}^{\prime }_{2C_r + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\psi _r)$
in each of the above cases. The fact that
![]() $\mathbf {T}^{\prime }_a \vdash \mathbf {T}^{\prime }_b$
, for any
$\mathbf {T}^{\prime }_a \vdash \mathbf {T}^{\prime }_b$
, for any
![]() $0 \leq b \leq a \in \mathbb {N}$
, will be used repeatedly without mention.
$0 \leq b \leq a \in \mathbb {N}$
, will be used repeatedly without mention.
-
(Axiom) Suppose that
 $\psi _r$
is an axiom in
$\psi _r$
is an axiom in
 $\Gamma $
. We have
$\Gamma $
. We have
 $\mathbf {T}^{\prime }_k \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\phi _r)$
, since
$\mathbf {T}^{\prime }_k \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\phi _r)$
, since
 $\mathbf {T}^{\prime }_k \vdash \mathbf {T}_{k+A'}$
and
$\mathbf {T}^{\prime }_k \vdash \mathbf {T}_{k+A'}$
and
 $\mathbf {T}_{k+A'} \vdash \mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{\underline {k+A'}}(\phi _r)$
.
$\mathbf {T}_{k+A'} \vdash \mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}_{\underline {k+A'}}(\phi _r)$
. -
(First-order) By (IH),
 $\mathbf {T}^{\prime }_{2C_r + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\phi _q)$
, for each
$\mathbf {T}^{\prime }_{2C_r + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\phi _q)$
, for each
 $q < r$
. Since
$q < r$
. Since
 $\mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}$
is an interpretation, it respects the inference rules of first-order logic. Therefore,
$\mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}$
is an interpretation, it respects the inference rules of first-order logic. Therefore,
 $\mathbf {T}^{\prime }_{2C_r + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\psi _r)$
.
$\mathbf {T}^{\prime }_{2C_r + k} \vdash \mathcal {I}^{\mathrm {Uni}^{\prime }, \mathrm {Mod}^{\prime }_0}_{\underline {k}}(\psi _r)$
. -
(NEC) In this case
 $\psi _r$
is
$\psi _r$
is
 $\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} (\mathsf {Mod}(\mathcal {U}, \ulcorner \psi _{r'} \urcorner ))$
. Note that
$\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} (\mathsf {Mod}(\mathcal {U}, \ulcorner \psi _{r'} \urcorner ))$
. Note that
 $C_r = 0$
and
$C_r = 0$
and
 $N_{r'} < N_r$
.
$N_{r'} < N_r$
.  $$ \begin{align*} \mathbf{T}^{\prime}_{k-1} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k-1}}(\psi_{r'}) & & \text{(IH)} \\ \mathbf{T}^{\prime}_{k} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{k}} \hspace{2pt} ( \mathcal{U} \models \ulcorner \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k-1}}(\psi_{r'}) \urcorner) & & \mathsf{NEC}^* \\ \mathbf{T}^{\prime}_{k} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{k}} \hspace{2pt} (\mathrm{Mod}^{\prime}_{\underline{k}}(\mathcal{U}, \ulcorner \psi_{r'} \urcorner)) & & (\dagger)\ \text{in Construction 3.2} \\ \mathbf{T}^{\prime}_{k} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}} \big(\forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} (\mathsf{Mod}(\mathcal{U}, \ulcorner \psi_{r'} \urcorner)) \big) & & \text{Definition of } \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}} \end{align*} $$
$$ \begin{align*} \mathbf{T}^{\prime}_{k-1} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k-1}}(\psi_{r'}) & & \text{(IH)} \\ \mathbf{T}^{\prime}_{k} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{k}} \hspace{2pt} ( \mathcal{U} \models \ulcorner \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k-1}}(\psi_{r'}) \urcorner) & & \mathsf{NEC}^* \\ \mathbf{T}^{\prime}_{k} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{k}} \hspace{2pt} (\mathrm{Mod}^{\prime}_{\underline{k}}(\mathcal{U}, \ulcorner \psi_{r'} \urcorner)) & & (\dagger)\ \text{in Construction 3.2} \\ \mathbf{T}^{\prime}_{k} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}} \big(\forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} (\mathsf{Mod}(\mathcal{U}, \ulcorner \psi_{r'} \urcorner)) \big) & & \text{Definition of } \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}} \end{align*} $$
-
(CONEC) In this case
 $\psi _{r'}$
is
$\psi _{r'}$
is
 $\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} (\mathsf {Mod}(\mathcal {U}, \ulcorner \psi _{r} \urcorner ))$
.
$\forall \mathcal {U} \in \mathsf {Uni}\hspace {2pt} (\mathsf {Mod}(\mathcal {U}, \ulcorner \psi _{r} \urcorner ))$
.  $$ \begin{align*} \mathbf{T}^{\prime}_{2C_{r'} + k+1} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k+1}} \big(\forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} (\mathsf{Mod}(\mathcal{U}, \ulcorner \psi_r \urcorner))\big) & & \text{(IH)} \\ \mathbf{T}^{\prime}_{2C_{r'} + k+1} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{k + 1}} \hspace{2pt} (\mathrm{Mod}^{\prime}_{\underline{k + 1}}(\mathcal{U}, \ulcorner \psi_r \urcorner)) & & \text{Definition of } \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k+1}} \\ \mathbf{T}^{\prime}_{2C_{r'} + k+1} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{k + 1}} \hspace{2pt} (\mathcal{U} \models \ulcorner \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}}(\psi_r) \urcorner) & & (\dagger)\ \text{in Construction 3.2} \\ \mathbf{T}^{\prime}_{2C_{r'} + k+1} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{2C_{r'} + k+1}} \hspace{2pt} (\mathcal{U} \models \ulcorner \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}}(\psi_r) \urcorner) & & \mathbf{Uni}^{\prime}_{\underline{2C_{r'} + k+1}} \subseteq \mathbf{Uni}^{\prime}_{\underline{k + 1}} \\ \mathbf{T}^{\prime}_{2C_{r'} + k+2} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}}(\psi_r) & & \mathsf{CONEC}^* \\ \mathbf{T}^{\prime}_{2C_r + k} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}}(\psi_r) & & C_{r'} < C_r \end{align*} $$
$$ \begin{align*} \mathbf{T}^{\prime}_{2C_{r'} + k+1} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k+1}} \big(\forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} (\mathsf{Mod}(\mathcal{U}, \ulcorner \psi_r \urcorner))\big) & & \text{(IH)} \\ \mathbf{T}^{\prime}_{2C_{r'} + k+1} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{k + 1}} \hspace{2pt} (\mathrm{Mod}^{\prime}_{\underline{k + 1}}(\mathcal{U}, \ulcorner \psi_r \urcorner)) & & \text{Definition of } \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k+1}} \\ \mathbf{T}^{\prime}_{2C_{r'} + k+1} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{k + 1}} \hspace{2pt} (\mathcal{U} \models \ulcorner \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}}(\psi_r) \urcorner) & & (\dagger)\ \text{in Construction 3.2} \\ \mathbf{T}^{\prime}_{2C_{r'} + k+1} &\vdash \forall \mathcal{U} \in \mathbf{Uni}^{\prime}_{\underline{2C_{r'} + k+1}} \hspace{2pt} (\mathcal{U} \models \ulcorner \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}}(\psi_r) \urcorner) & & \mathbf{Uni}^{\prime}_{\underline{2C_{r'} + k+1}} \subseteq \mathbf{Uni}^{\prime}_{\underline{k + 1}} \\ \mathbf{T}^{\prime}_{2C_{r'} + k+2} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}}(\psi_r) & & \mathsf{CONEC}^* \\ \mathbf{T}^{\prime}_{2C_r + k} &\vdash \mathcal{I}^{\mathrm{Uni}^{\prime}, \mathrm{Mod}^{\prime}_0}_{\underline{k}}(\psi_r) & & C_{r'} < C_r \end{align*} $$
This completes the proof of the lemma. We close by recording the more detailed statement that we have actually proved: If
![]() $N,C$
are the number of applications of
$N,C$
are the number of applications of
![]() $\mathsf {NEC}$
and
$\mathsf {NEC}$
and
![]() $\mathsf {CONEC}$
, respectively, in a proof of
$\mathsf {CONEC}$
, respectively, in a proof of
![]() $\psi $
in
$\psi $
in
![]() $\mathsf {MS}^-_{\mathrm {NC}} + S$
, then
$\mathsf {MS}^-_{\mathrm {NC}} + S$
, then
□
Corollary 5.2. Let
![]() $\mathrm {T}$
,
$\mathrm {T}$
,
![]() $\mathrm {Uni}$
and
$\mathrm {Uni}$
and
![]() $\mathrm {Mod}_0$
be revision parameters such that for some
$\mathrm {Mod}_0$
be revision parameters such that for some
![]() $B \in \mathbb {N}$
,
$B \in \mathbb {N}$
,
![]() $\mathbf {T}_B \vdash \mathsf {ZF}$
. Let
$\mathbf {T}_B \vdash \mathsf {ZF}$
. Let
![]() $\mathfrak {F} = \{\mathcal {I}_{\underline {k}} \mid k \in \mathbb {N}\}$
and let S be a theory (possibly with
$\mathfrak {F} = \{\mathcal {I}_{\underline {k}} \mid k \in \mathbb {N}\}$
and let S be a theory (possibly with
![]() $\mathsf {Uni}, \mathsf {Mod}$
in its language) such that for any finite
$\mathsf {Uni}, \mathsf {Mod}$
in its language) such that for any finite
![]() $\Gamma \subseteq S$
,
$\Gamma \subseteq S$
,
-
(a) If
 $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
 $\mathsf {NEC}^*$
, then
$\mathsf {NEC}^*$
, then
 $\mathbf {T}_\omega $
locally interprets
$\mathbf {T}_\omega $
locally interprets
 $\mathsf {CM} + \mathsf {NEC} + S$
by
$\mathsf {CM} + \mathsf {NEC} + S$
by
 $\mathfrak {F}$
.
$\mathfrak {F}$
. -
(b) If
 $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
 $\mathsf {CONEC}^*$
, then
$\mathsf {CONEC}^*$
, then
 $\mathbf {T}_\omega $
locally interprets
$\mathbf {T}_\omega $
locally interprets
 $\mathsf {CM} + \mathsf {CONEC} + S$
by
$\mathsf {CM} + \mathsf {CONEC} + S$
by
 $\mathfrak {F}$
.
$\mathfrak {F}$
. -
(c) If
 $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
admit
 $\mathsf {NEC}^*$
and
$\mathsf {NEC}^*$
and
 $\mathsf {CONEC}^*$
, then
$\mathsf {CONEC}^*$
, then
 $\mathbf {T}_\omega $
locally interprets
$\mathbf {T}_\omega $
locally interprets
 $\mathsf {MS} + S$
by
$\mathsf {MS} + S$
by
 $\mathfrak {F}$
.
$\mathfrak {F}$
.
Proof. Let
![]() $B \in \mathbb {N}$
, such that
$B \in \mathbb {N}$
, such that
![]() $\mathbf {T}_B \vdash \mathsf {ZF}$
. Since
$\mathbf {T}_B \vdash \mathsf {ZF}$
. Since
![]() $\mathrm {T}$
,
$\mathrm {T}$
,
![]() $\mathrm {Uni}$
and
$\mathrm {Uni}$
and
![]() $\mathrm {Mod}_0$
are revision parameters, we have
$\mathrm {Mod}_0$
are revision parameters, we have
So by the definition of
![]() $\mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}$
and (
$\mathcal {I}^{\mathrm {Uni}, \mathrm {Mod}_0}$
and (
![]() $\dagger $
) in Construction 3.2,
$\dagger $
) in Construction 3.2,
Applying the Main Lemma with
![]() $S + \mathsf {Multiverse}_{\mathsf {ZF}}$
for S, and the maximum of A and
$S + \mathsf {Multiverse}_{\mathsf {ZF}}$
for S, and the maximum of A and
![]() $B+1$
for A, we obtain the desired result.□
$B+1$
for A, we obtain the desired result.□
The following systems, along with
![]() $\mathsf {GR}^\alpha $
from Definition 2.8, are useful for measuring the consistency strength of various extensions of
$\mathsf {GR}^\alpha $
from Definition 2.8, are useful for measuring the consistency strength of various extensions of
![]() $\mathsf {CM}$
.
$\mathsf {CM}$
.
System 5.3. Let S be a set-theoretic system. For any set theory T in language L,
![]() $\mathrm {R}_T$
is the so called (proof-theoretic) Reflection schema:
$\mathrm {R}_T$
is the so called (proof-theoretic) Reflection schema:
(The dot under T is sometimes omitted, when it is clear from the context.)
We recursively define, for recursive ordinalsFootnote
13
![]() $\alpha $
, the theories
$\alpha $
, the theories
![]() $\mathsf {Con}^\alpha (S)$
and
$\mathsf {Con}^\alpha (S)$
and
![]() $\mathsf {R}^\alpha (S)$
, of
$\mathsf {R}^\alpha (S)$
, of
![]() $\alpha $
-iterated Consistency over S and
$\alpha $
-iterated Consistency over S and
![]() $\alpha $
-iterated Reflection schema over S, respectively:
$\alpha $
-iterated Reflection schema over S, respectively:
 $$ \begin{align*} \mathsf{Con}^0(S) &=_{\mathrm{df}} S; \\ \mathsf{Con}^{\alpha+1}(S) &=_{\mathrm{df}} \mathsf{Con}^\alpha(S) + \mathrm{Con}_{\mathsf{Con}^\alpha(S)}; \\ \mathsf{Con}^\alpha(S) &=_{\mathrm{df}} \bigcup_{\xi < \alpha} \mathsf{Con}^\xi(S) \text{, for }\alpha\text{ a limit ordinal}; \\ \mathsf{R}^0(S) &=_{\mathrm{df}} S; \\ \mathsf{R}^{\alpha+1}(S) &=_{\mathrm{df}} \mathsf{R}^\alpha(S) + \mathrm{R}_{\mathsf{R}^\alpha(S)}; \\ \mathsf{R}^\alpha(S) &=_{\mathrm{df}} \bigcup_{\xi < \alpha} \mathsf{R}^\xi(S) \text{, for }\alpha\text{ a limit ordinal.} \end{align*} $$
$$ \begin{align*} \mathsf{Con}^0(S) &=_{\mathrm{df}} S; \\ \mathsf{Con}^{\alpha+1}(S) &=_{\mathrm{df}} \mathsf{Con}^\alpha(S) + \mathrm{Con}_{\mathsf{Con}^\alpha(S)}; \\ \mathsf{Con}^\alpha(S) &=_{\mathrm{df}} \bigcup_{\xi < \alpha} \mathsf{Con}^\xi(S) \text{, for }\alpha\text{ a limit ordinal}; \\ \mathsf{R}^0(S) &=_{\mathrm{df}} S; \\ \mathsf{R}^{\alpha+1}(S) &=_{\mathrm{df}} \mathsf{R}^\alpha(S) + \mathrm{R}_{\mathsf{R}^\alpha(S)}; \\ \mathsf{R}^\alpha(S) &=_{\mathrm{df}} \bigcup_{\xi < \alpha} \mathsf{R}^\xi(S) \text{, for }\alpha\text{ a limit ordinal.} \end{align*} $$
We use the notations
![]() $\mathsf {Con}^\alpha $
and
$\mathsf {Con}^\alpha $
and
![]() $\mathsf {R}^\alpha $
for
$\mathsf {R}^\alpha $
for
![]() $\mathsf {Con}^\alpha (\mathsf {ZF})$
and
$\mathsf {Con}^\alpha (\mathsf {ZF})$
and
![]() $\mathsf {R}^\alpha (\mathsf {ZF})$
, respectively.
$\mathsf {R}^\alpha (\mathsf {ZF})$
, respectively.
Recall System 2.8, where
![]() $\mathsf {GR}^\alpha $
is defined, using the axiom
$\mathsf {GR}^\alpha $
is defined, using the axiom
![]() $\mathsf {GR}_T$
of Global Reflection over a set theory T extending
$\mathsf {GR}_T$
of Global Reflection over a set theory T extending
![]() $\mathsf {CT}\hspace {-3pt}\restriction $
(in some language
$\mathsf {CT}\hspace {-3pt}\restriction $
(in some language
![]() $L_{\mathsf {Sat}}$
with a satisfaction predicate):
$L_{\mathsf {Sat}}$
with a satisfaction predicate):
Comparing
![]() $\mathsf {R}_T$
with
$\mathsf {R}_T$
with
![]() $\mathsf {GR}_T$
, note that
$\mathsf {GR}_T$
, note that
![]() $\mathsf {R}_T$
is a schema, with a separate axiom for each formula of the form
$\mathsf {R}_T$
is a schema, with a separate axiom for each formula of the form
![]() $\phi $
in the meta-language, while
$\phi $
in the meta-language, while
![]() $\mathsf {GR}_T$
quantifies internally over all formulas in the object-language; the latter is made possible by the satisfaction/truth-predicate.
$\mathsf {GR}_T$
quantifies internally over all formulas in the object-language; the latter is made possible by the satisfaction/truth-predicate.
Remark. Let us pause to measure the consistency strengths of
![]() $\mathsf {GR}^\omega $
,
$\mathsf {GR}^\omega $
,
![]() $\mathsf {R}^\omega $
and
$\mathsf {R}^\omega $
and
![]() $\mathsf {Con}^\omega $
: The consistency strength of
$\mathsf {Con}^\omega $
: The consistency strength of
![]() $\mathsf {GR}^\omega $
is bounded by that of
$\mathsf {GR}^\omega $
is bounded by that of
![]() $\mathsf {MK} + \mathsf {GC}$
(Morse–Kelley class theory with Global Choice),Footnote
14
which, in turn, is far less than that of
$\mathsf {MK} + \mathsf {GC}$
(Morse–Kelley class theory with Global Choice),Footnote
14
which, in turn, is far less than that of
![]() $\mathsf {ZFC} + \text {“there exists an inaccessible cardinal.”}$
Footnote
15
The consistency strength of
$\mathsf {ZFC} + \text {“there exists an inaccessible cardinal.”}$
Footnote
15
The consistency strength of
![]() $\mathsf {R}^\omega $
is bounded by that of
$\mathsf {R}^\omega $
is bounded by that of
![]() $\mathsf {GR}^1$
.Footnote
16
The consistency strength of
$\mathsf {GR}^1$
.Footnote
16
The consistency strength of
![]() $\mathsf {Con}^\omega $
is bounded by that of
$\mathsf {Con}^\omega $
is bounded by that of
![]() $\mathsf {R}^1$
.Footnote
17
Moreover, it is easily observed that for each
$\mathsf {R}^1$
.Footnote
17
Moreover, it is easily observed that for each
![]() $n \in \mathbb {N}$
:
$n \in \mathbb {N}$
:
![]() $\mathsf {GR}^{n+1}$
,
$\mathsf {GR}^{n+1}$
,
![]() $\mathsf {R}^{n+1}$
and
$\mathsf {R}^{n+1}$
and
![]() $\mathsf {Con}^{n+1}$
proves the consistency of
$\mathsf {Con}^{n+1}$
proves the consistency of
![]() $\mathsf {GR}^{n}$
,
$\mathsf {GR}^{n}$
,
![]() $\mathsf {R}^{n}$
and
$\mathsf {R}^{n}$
and
![]() $\mathsf {Con}^{n}$
, respectively.
$\mathsf {Con}^{n}$
, respectively.
Theorem 5.4.
![]() $\mathsf {Con}^\omega $
locally interprets
$\mathsf {Con}^\omega $
locally interprets
![]() $\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality}$
.
$\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality}$
.
Proof. We can choose revision parameters
![]() $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
, such that for each
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
, such that for each
![]() $n \in \mathbb {N}$
:
$n \in \mathbb {N}$
:
 $$ \begin{align*} \mathbf{T}_n &= \mathsf{Con}^n, \\ \mathbf{Uni}_{n+1} &= \{ \mathcal{U} \mid \mathcal{U} \models \mathbf{T}_n \}. \end{align*} $$
$$ \begin{align*} \mathbf{T}_n &= \mathsf{Con}^n, \\ \mathbf{Uni}_{n+1} &= \{ \mathcal{U} \mid \mathcal{U} \models \mathbf{T}_n \}. \end{align*} $$
Clearly, these are revision parameters provably satisfying
![]() $\textsf {Soundness}^*$
, and thereby admitting
$\textsf {Soundness}^*$
, and thereby admitting
![]() $\mathsf {NEC}^*$
. Moreover, we have for each
$\mathsf {NEC}^*$
. Moreover, we have for each
![]() $k \in \mathbb {N}$
:
$k \in \mathbb {N}$
:
 $$ \begin{align*} \mathbf{T}_{k+1} &\vdash \mathbf{Uni}_{\underline{k+1}} \neq \varnothing & & \text{Definition of } \mathbf{T}_{k+1}, \mathbf{Uni}_{k+1}, \\ \mathbf{T}_{k+1} &\vdash \mathcal{I}^{\mathrm{Uni}, \mathrm{Mod}_0}_{\underline{k+1}}(\textsf{Non-Triviality}) & & \text{Definition of } \mathcal{I}^{\mathrm{Uni}, \mathrm{Mod}_0}_{\underline{k+1}}. \end{align*} $$
$$ \begin{align*} \mathbf{T}_{k+1} &\vdash \mathbf{Uni}_{\underline{k+1}} \neq \varnothing & & \text{Definition of } \mathbf{T}_{k+1}, \mathbf{Uni}_{k+1}, \\ \mathbf{T}_{k+1} &\vdash \mathcal{I}^{\mathrm{Uni}, \mathrm{Mod}_0}_{\underline{k+1}}(\textsf{Non-Triviality}) & & \text{Definition of } \mathcal{I}^{\mathrm{Uni}, \mathrm{Mod}_0}_{\underline{k+1}}. \end{align*} $$
So the result follows from Corollary 5.2, by setting
![]() $S = \{\textsf {Non-Triviality}\}$
.□
$S = \{\textsf {Non-Triviality}\}$
.□
Remark. Under the mild meta-theoretic assumption that each
![]() $\mathsf {Con}^n$
is closed under the Reflection rule, it follows from Lemma 3.3 that the revision parameters in the above proof admit
$\mathsf {Con}^n$
is closed under the Reflection rule, it follows from Lemma 3.3 that the revision parameters in the above proof admit
![]() $\mathsf {CONEC}^*$
, yielding that
$\mathsf {CONEC}^*$
, yielding that
![]() $\mathsf {Con}^\omega $
locally interprets
$\mathsf {Con}^\omega $
locally interprets
![]() $\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality}$
. This meta-theoretic assumption follows from the assumption that
$\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality}$
. This meta-theoretic assumption follows from the assumption that
![]() $\mathsf {Con}^\omega $
is
$\mathsf {Con}^\omega $
is
![]() $\omega $
-consistent, which in turn follows from the existence of an
$\omega $
-consistent, which in turn follows from the existence of an
![]() $\omega $
-standard model of
$\omega $
-standard model of
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Remark. Using the fine-grained result obtained at the end of the proof of the Main Lemma, we can show by an overspill-argument that
![]() $\mathsf {Con}^\omega + \{\underline {n} < c \mid n \in \mathbb {N}\}$
(for a fresh constant c) interprets
$\mathsf {Con}^\omega + \{\underline {n} < c \mid n \in \mathbb {N}\}$
(for a fresh constant c) interprets
![]() $\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality}$
(not just locally). This raises:
$\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality}$
(not just locally). This raises:
Question. Is
![]() $\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality} \omega $
-inconsistent?
$\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality} \omega $
-inconsistent?
Theorem 5.5.
![]() $\mathsf {R}^\omega $
locally interprets
$\mathsf {R}^\omega $
locally interprets
![]() $\mathsf {MS} + \textsf {Multiverse Reflection}$
.
$\mathsf {MS} + \textsf {Multiverse Reflection}$
.
Proof. We can choose revision parameters
![]() $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
, such that for each
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
, such that for each
![]() $n \in \mathbb {N}$
:
$n \in \mathbb {N}$
:
 $$ \begin{align*} \mathbf{T}_n &= \mathsf{R}^n, \\ \mathbf{Uni}_{n+1} &= \{ \mathcal{U} \mid \mathcal{U} \models \mathbf{T}_n \}. \end{align*} $$
$$ \begin{align*} \mathbf{T}_n &= \mathsf{R}^n, \\ \mathbf{Uni}_{n+1} &= \{ \mathcal{U} \mid \mathcal{U} \models \mathbf{T}_n \}. \end{align*} $$
It is easily seen that these are revision parameters provably satisfying
![]() $\textsf {Soundness}^*$
, and thereby admitting
$\textsf {Soundness}^*$
, and thereby admitting
![]() $\mathsf {NEC}^*$
. Similarly, it is easily seen that they admit the
$\mathsf {NEC}^*$
. Similarly, it is easily seen that they admit the
![]() $\textsf {Reflection rule}^*$
and satisfy
$\textsf {Reflection rule}^*$
and satisfy
![]() $\textsf {Completeness}^*$
, so that they admit
$\textsf {Completeness}^*$
, so that they admit
![]() $\mathsf {CONEC}^*$
. Moreover, we have for each
$\mathsf {CONEC}^*$
. Moreover, we have for each
![]() $k \in \mathbb {N}$
and each
$k \in \mathbb {N}$
and each
![]() $\phi \in \mathcal {L}$
:
$\phi \in \mathcal {L}$
:
 $$ \begin{align*} \mathbf{T}_{k+1} &\vdash \big( \forall \mathcal{U} \in \mathbf{Uni}_{\underline{k+1}} \hspace{2pt} \mathrm{Mod}_{\underline{k+1}}(\mathcal{U}, \ulcorner \phi \urcorner) \big) \rightarrow \phi & & \text{The completeness theorem and} \\ & & & \text{the definition of } \mathbf{T}_{k+1}, \mathbf{Uni}_{k+1} \\ \mathbf{T}_{k+1} &\vdash \mathcal{I}^{\mathrm{Uni}, \mathrm{Mod}_0}_{\underline{k+1}}(\mathsf{Tr}^\Box(\ulcorner \phi \urcorner) \rightarrow \phi) & & \text{Definition of } \mathcal{I}^{\mathrm{Uni}, \mathrm{Mod}_0}_{\underline{k+1}} \end{align*} $$
$$ \begin{align*} \mathbf{T}_{k+1} &\vdash \big( \forall \mathcal{U} \in \mathbf{Uni}_{\underline{k+1}} \hspace{2pt} \mathrm{Mod}_{\underline{k+1}}(\mathcal{U}, \ulcorner \phi \urcorner) \big) \rightarrow \phi & & \text{The completeness theorem and} \\ & & & \text{the definition of } \mathbf{T}_{k+1}, \mathbf{Uni}_{k+1} \\ \mathbf{T}_{k+1} &\vdash \mathcal{I}^{\mathrm{Uni}, \mathrm{Mod}_0}_{\underline{k+1}}(\mathsf{Tr}^\Box(\ulcorner \phi \urcorner) \rightarrow \phi) & & \text{Definition of } \mathcal{I}^{\mathrm{Uni}, \mathrm{Mod}_0}_{\underline{k+1}} \end{align*} $$
So the result follows from Corollary 5.2, by setting
![]() $S ={\textsf {Multiverse Reflection}}$
.□
$S ={\textsf {Multiverse Reflection}}$
.□
Remark. The technique for obtaining full (not just local) interpretability, mentioned in the second remark following Theorem 5.4, does not work for the above theorem, because Multiverse Reflection is not finitely axiomatizable (as far as the authors can see). The overspill-argument must be carried out on a single formula, not a schema.
Theorem 5.6. The following conservativity results hold:
-
(a)
 $\mathsf {Comp}_{\mathsf {CM}} \equiv _{\mathcal {L}} \mathsf {ZF}$
.
$\mathsf {Comp}_{\mathsf {CM}} \equiv _{\mathcal {L}} \mathsf {ZF}$
. -
(b)
 $\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality} \equiv _{\mathcal {L}} \mathsf {Con}^\omega $
.
$\mathsf {CM} + \mathsf {NEC} + \textsf {Non-Triviality} \equiv _{\mathcal {L}} \mathsf {Con}^\omega $
. -
(c)
 $\mathsf {MS} + \textsf {Multiverse Reflection} \equiv _{\mathcal {L}} \mathsf {CM} + \mathsf {NEC} + \textsf {Multiverse Reflection} \equiv _{\mathcal {L}} \mathsf {R}^\omega $
.
$\mathsf {MS} + \textsf {Multiverse Reflection} \equiv _{\mathcal {L}} \mathsf {CM} + \mathsf {NEC} + \textsf {Multiverse Reflection} \equiv _{\mathcal {L}} \mathsf {R}^\omega $
.
Proof.
-
(a) This is immediate from Theorem 4.8(c) and that the interpretation used in its proof restricts to the identity on
 $\mathcal {L}$
.
$\mathcal {L}$
. -
(b) The right-to-left direction follows from Theorem 5.4, observing that the interpretation is the identity on
 $\mathcal {L}$
.
$\mathcal {L}$
.For the left-to-right direction, suppose as induction hypothesis that we have proved
 $\mathsf {Con}^n$
in
$\mathsf {Con}^n$
in
 $\mathsf {CM} +\mathsf {NEC} + \textsf { Non-Triviality}$
. By
$\mathsf {CM} +\mathsf {NEC} + \textsf { Non-Triviality}$
. By
 $\mathsf {NEC}$
, we have
$\mathsf {NEC}$
, we have
 $\mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{{\mathsf {Con}}^{\underline {n}}})$
. So by Non-Triviality and Lemma 4.4, we can prove
$\mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{{\mathsf {Con}}^{\underline {n}}})$
. So by Non-Triviality and Lemma 4.4, we can prove
 $\mathsf {Con}^n + \mathrm {Con}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {Con}}^{\underline {n}})$
, which is
$\mathsf {Con}^n + \mathrm {Con}(\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {Con}}^{\underline {n}})$
, which is
 $\mathsf {Con}^{n+1}$
, as desired.
$\mathsf {Con}^{n+1}$
, as desired. -
(c) That
 $\mathsf {R}^\omega $
proves every
$\mathsf {R}^\omega $
proves every
 $\mathcal {L}$
-theorem of
$\mathcal {L}$
-theorem of
 $\mathsf {MS} + \textsf {Multiverse Reflection}$
follows from Theorem 5.5, observing that the interpretation is the identity on
$\mathsf {MS} + \textsf {Multiverse Reflection}$
follows from Theorem 5.5, observing that the interpretation is the identity on
 $\mathcal {L}$
.
$\mathcal {L}$
.That
 $\mathsf {MS} + \textsf {Multiverse Reflection} \vdash \mathsf {CM} + \mathsf {NEC} + \textsf {Multiverse Reflection}$
is trivial.
$\mathsf {MS} + \textsf {Multiverse Reflection} \vdash \mathsf {CM} + \mathsf {NEC} + \textsf {Multiverse Reflection}$
is trivial.For
 $\mathsf {CM} + \mathsf {NEC} + \textsf {Multiverse Reflection} \vdash \mathsf {R}^\omega $
, we shall show that for each
$\mathsf {CM} + \mathsf {NEC} + \textsf {Multiverse Reflection} \vdash \mathsf {R}^\omega $
, we shall show that for each
 $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
 $\mathsf {CM} + \mathsf {NEC} + \textsf {Multiverse Reflection} \vdash \mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\underline {n}})$
. Then the result follows from
$\mathsf {CM} + \mathsf {NEC} + \textsf {Multiverse Reflection} \vdash \mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\underline {n}})$
. Then the result follows from
 $\textsf {Multiverse Reflection}$
. We proceed by induction. By
$\textsf {Multiverse Reflection}$
. We proceed by induction. By
 $\textsf {Multiverse}_{\mathsf {ZF}}$
, we have the base case:
$\textsf {Multiverse}_{\mathsf {ZF}}$
, we have the base case:
 $\mathsf {MS} + \textsf { Multiverse Reflection} \vdash \mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\underline {0}}).$
So suppose as induction hypothesis that Let
$\mathsf {MS} + \textsf { Multiverse Reflection} \vdash \mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\underline {0}}).$
So suppose as induction hypothesis that Let $$ \begin{align*} \mathsf{MS} + \textsf{Multiverse Reflection} \vdash \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathsf{R}}^{\underline{k}}). \end{align*} $$
$$ \begin{align*} \mathsf{MS} + \textsf{Multiverse Reflection} \vdash \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathsf{R}}^{\underline{k}}). \end{align*} $$
 $\sigma \in \mathrm {Sent}(\mathcal {L})$
. By
$\sigma \in \mathrm {Sent}(\mathcal {L})$
. By
 $\mathsf {NEC}$
we have (1)
$\mathsf {NEC}$
we have (1) $$ \begin{align} \mathsf{MS} + \textsf{Multiverse Reflection} &\vdash \mathsf{Tr}^\Box(\ulcorner \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathsf{R}}^{\underline{k}}) \urcorner), \end{align} $$
(2)
$$ \begin{align} \mathsf{MS} + \textsf{Multiverse Reflection} &\vdash \mathsf{Tr}^\Box(\ulcorner \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathsf{R}}^{\underline{k}}) \urcorner), \end{align} $$
(2) $$ \begin{align} \mathsf{MS} + \textsf{Multiverse Reflection} &\vdash \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathsf{CM}}), \end{align} $$
(3)since (by Multiverse
$$ \begin{align} \mathsf{MS} + \textsf{Multiverse Reflection} &\vdash \mathsf{Tr}^\Box(\underset{\substack{\\[-9.5pt]\mbox{.}}}{\mathsf{CM}}), \end{align} $$
(3)since (by Multiverse $$ \begin{align} \mathsf{MS} + \textsf{Multiverse Reflection} &\vdash \mathsf{Tr}^\Box(\ulcorner \mathsf{Tr}^\Box(\ulcorner \sigma \urcorner) \rightarrow \sigma \urcorner), \end{align} $$
$$ \begin{align} \mathsf{MS} + \textsf{Multiverse Reflection} &\vdash \mathsf{Tr}^\Box(\ulcorner \mathsf{Tr}^\Box(\ulcorner \sigma \urcorner) \rightarrow \sigma \urcorner), \end{align} $$
 $_{\mathsf {ZF}}$
)
$_{\mathsf {ZF}}$
)
 $\mathsf {NEC}$
only needs to be applied to finitely many axioms of
$\mathsf {NEC}$
only needs to be applied to finitely many axioms of
 $\mathsf {CM}$
. We work in
$\mathsf {CM}$
. We work in
 $\mathsf {MS} + \textsf {Multiverse Reflection}$
. Let
$\mathsf {MS} + \textsf {Multiverse Reflection}$
. Let
 $\mathcal {U} \in \mathsf {Uni}$
. Assume
$\mathcal {U} \in \mathsf {Uni}$
. Assume
 $\mathsf {Mod}(\mathcal {U}, \ulcorner \Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\underline {k}}}(\ulcorner \sigma \urcorner ) \urcorner ).$
We shall show
$\mathsf {Mod}(\mathcal {U}, \ulcorner \Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\underline {k}}}(\ulcorner \sigma \urcorner ) \urcorner ).$
We shall show
 $\mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner )$
. By (2), we can apply the Soundness Lemma in
$\mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner )$
. By (2), we can apply the Soundness Lemma in
 $\mathcal {U}$
to obtain
$\mathcal {U}$
to obtain
 $\mathsf {Mod}(\mathcal {U}, \ulcorner \mathsf {Tr}^\Box (\ulcorner \sigma \urcorner ) \urcorner )$
from (1) and
$\mathsf {Mod}(\mathcal {U}, \ulcorner \mathsf {Tr}^\Box (\ulcorner \sigma \urcorner ) \urcorner )$
from (1) and
 $\mathsf {Mod}(\mathcal {U}, \ulcorner \Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\underline {k}}}(\ulcorner \sigma \urcorner ) \urcorner )$
. Now by
$\mathsf {Mod}(\mathcal {U}, \ulcorner \Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\underline {k}}}(\ulcorner \sigma \urcorner ) \urcorner )$
. Now by
 $\mathsf {CM}_\rightarrow $
and (3), we obtain
$\mathsf {CM}_\rightarrow $
and (3), we obtain
 $\mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner )$
, as desired.
$\mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner )$
, as desired.
□
Theorem 5.7.
![]() $\mathsf {GR}^\omega $
interprets
$\mathsf {GR}^\omega $
interprets
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
.
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
.
Proof. Set
![]() $\mathcal {L}^{\mathrm {T}} = \mathcal {L}_{\mathsf {Sat}, \iota , \mathsf {self}}$
and set
$\mathcal {L}^{\mathrm {T}} = \mathcal {L}_{\mathsf {Sat}, \iota , \mathsf {self}}$
and set
![]() $\mathcal {L}^{\mathrm {Rev}}$
to
$\mathcal {L}^{\mathrm {Rev}}$
to
![]() $\mathcal {L}_{\iota , \mathsf {self}}$
. We can choose revision parameters
$\mathcal {L}_{\iota , \mathsf {self}}$
. We can choose revision parameters
![]() $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
, such that for each
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
, such that for each
![]() $n \in \mathbb {N}$
:
$n \in \mathbb {N}$
:
 $$ \begin{align*} \mathbf{T}_n &= \mathsf{SP}^n, \\ \mathbf{Uni}_{n+1} &= \{\mathcal{U} \mid \mathcal{U} \models \mathbf{T}_{n} \wedge \mathcal{U} \in \mathbf{crsm}\}. \end{align*} $$
$$ \begin{align*} \mathbf{T}_n &= \mathsf{SP}^n, \\ \mathbf{Uni}_{n+1} &= \{\mathcal{U} \mid \mathcal{U} \models \mathbf{T}_{n} \wedge \mathcal{U} \in \mathbf{crsm}\}. \end{align*} $$
Clearly these are revision parameters satisfying
![]() $\textsf {Soundness}^*$
, thus admitting
$\textsf {Soundness}^*$
, thus admitting
![]() $\mathsf {NEC}^*$
. Moreover, note that for each
$\mathsf {NEC}^*$
. Moreover, note that for each
![]() $k < \omega $
,
$k < \omega $
,
![]() $\mathbf {T}_k \vdash \mathrm {Uni}_{\underline {k}}(\mathsf {self})$
. So for each
$\mathbf {T}_k \vdash \mathrm {Uni}_{\underline {k}}(\mathsf {self})$
. So for each
![]() $k < \omega $
,
$k < \omega $
,
Thus, it follows from Corollary 5.2 that
![]() $\mathfrak {F} = \{\mathcal {I}_{\underline {k}} \mid k < \omega \}$
is a local interpretation of
$\mathfrak {F} = \{\mathcal {I}_{\underline {k}} \mid k < \omega \}$
is a local interpretation of
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
in
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
in
![]() $\mathsf {SP}^\omega $
.
$\mathsf {SP}^\omega $
.
Recall from Lemma 2.19 that there is an interpretation
![]() $\mathcal {J}$
of
$\mathcal {J}$
of
![]() $\mathsf {SP}^\omega $
in
$\mathsf {SP}^\omega $
in
![]() $\mathsf {GR}^\omega $
. For each
$\mathsf {GR}^\omega $
. For each
![]() $n < \omega $
, let
$n < \omega $
, let
![]() $\mathcal {K}_{\underline {n}} = \mathcal {J} \circ \mathcal {I}_{\underline {n}}$
. Then
$\mathcal {K}_{\underline {n}} = \mathcal {J} \circ \mathcal {I}_{\underline {n}}$
. Then
![]() $\mathfrak {G} = \{\mathcal {K}_{\underline {k}} \mid k < \omega \}$
is a local interpretation of
$\mathfrak {G} = \{\mathcal {K}_{\underline {k}} \mid k < \omega \}$
is a local interpretation of
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
in
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
in
![]() $\mathsf {GR}^\omega $
. There is a technical hurdle later on in this proof caused by the fact that the image of each
$\mathsf {GR}^\omega $
. There is a technical hurdle later on in this proof caused by the fact that the image of each
![]() $\mathcal {K}_{\underline {n}}$
is not included in
$\mathcal {K}_{\underline {n}}$
is not included in
![]() $\mathcal {L}$
, but includes the instance of
$\mathcal {L}$
, but includes the instance of
![]() $\mathsf {Tr}$
needed to define the set
$\mathsf {Tr}$
needed to define the set
![]() $\mathbf {Tr} = \{\sigma \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\sigma )\}$
for the construction of
$\mathbf {Tr} = \{\sigma \in \mathrm {Sent}(\mathcal {L}_{\mathsf {Sat}}) \mid \mathsf {Tr}(\sigma )\}$
for the construction of
![]() $\mathcal {J}$
in the proof of Lemma 2.19. To overcome this, we construct the functions
$\mathcal {J}$
in the proof of Lemma 2.19. To overcome this, we construct the functions
![]() $\mathcal {K}^{\prime }_{\underline {n}}(\phi )$
, for each
$\mathcal {K}^{\prime }_{\underline {n}}(\phi )$
, for each
![]() $n < \omega $
, replacing each occurrence of the form “
$n < \omega $
, replacing each occurrence of the form “
![]() $\mathsf {Tr}(t)$
” in the values of
$\mathsf {Tr}(t)$
” in the values of
![]() $\mathcal {K}_{\underline {n}}$
by “
$\mathcal {K}_{\underline {n}}$
by “
![]() $t \in y$
,” where y is assumed to be fresh. Then we have for each
$t \in y$
,” where y is assumed to be fresh. Then we have for each
![]() $\phi $
that
$\phi $
that
Let f be a function enumerating the theorems of
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
, such that the length of the theorems is non-decreasing. Then, for each
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
, such that the length of the theorems is non-decreasing. Then, for each
![]() $i < \omega $
there is
$i < \omega $
there is
![]() $\sigma $
, such that
$\sigma $
, such that
![]() $\mathsf {GR}^\omega \vdash \underset {\substack {\\[-9.5pt]\mbox {.}}}{f}(\underline {i}) = \ulcorner \sigma \urcorner $
. Let
$\mathsf {GR}^\omega \vdash \underset {\substack {\\[-9.5pt]\mbox {.}}}{f}(\underline {i}) = \ulcorner \sigma \urcorner $
. Let
![]() $\theta (x, z)$
be the formula expressing
$\theta (x, z)$
be the formula expressing
Since the values of the
![]() $\mathcal {K}^{\prime }_{\underline {n}}$
are in
$\mathcal {K}^{\prime }_{\underline {n}}$
are in
![]() $\mathcal {L}$
, we have by Proposition 2.6 that for each
$\mathcal {L}$
, we have by Proposition 2.6 that for each
![]() $j < \omega $
and each
$j < \omega $
and each
![]() $\phi \in \mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
:
$\phi \in \mathcal {L}^{\mathrm {Rev}}_{\mathsf {Uni}, \mathsf {Mod}}$
:
So since
![]() $\mathfrak {G}$
is a local interpretation, we have for each
$\mathfrak {G}$
is a local interpretation, we have for each
![]() $n < \omega $
that
$n < \omega $
that
Since
![]() $\mathsf {GR}^\omega $
is
$\mathsf {GR}^\omega $
is
![]() $\omega $
-inconsistent, there is a formula
$\omega $
-inconsistent, there is a formula
![]() such that
such that
![]() , but for each
, but for each
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() . Working in
. Working in
![]() $\mathsf {GR}^\omega $
, employing Proposition 2.7, we obtain a maximal number
$\mathsf {GR}^\omega $
, employing Proposition 2.7, we obtain a maximal number
![]() $d < \omega $
such that
$d < \omega $
such that
![]() . Now there is a minimal number
. Now there is a minimal number
![]() $e < \omega $
such that
$e < \omega $
such that
So
![]() $\mathsf {GR}^\omega $
defines e by a formula
$\mathsf {GR}^\omega $
defines e by a formula
![]() $\psi $
. It follows from Proposition 2.6 that
$\psi $
. It follows from Proposition 2.6 that
![]() $\mathcal {K}_\psi $
is an interpretation of
$\mathcal {K}_\psi $
is an interpretation of
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
in
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
in
![]() $\mathsf {GR}^\omega $
.□
$\mathsf {GR}^\omega $
.□
Remark. Under the meta-theoretic assumption that the revision parameters used in the above proof admit the Reflection-rule*,
![]() $\mathsf {GR}^\omega $
interprets
$\mathsf {GR}^\omega $
interprets
![]() $\mathsf {MS}(\mathcal {L}_{\iota , \mathsf {self}}) + \textsf {Self-Perception}$
. Another potential approach to validating
$\mathsf {MS}(\mathcal {L}_{\iota , \mathsf {self}}) + \textsf {Self-Perception}$
. Another potential approach to validating
![]() $\mathsf {CONEC}$
would be to employ revision parameters based on a hierarchy of theories converging to
$\mathsf {CONEC}$
would be to employ revision parameters based on a hierarchy of theories converging to
![]() $\mathsf {FS}\hspace {-4pt}\restriction {} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
, rather than to
$\mathsf {FS}\hspace {-4pt}\restriction {} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
, rather than to
![]() $\mathsf {GR}^\omega $
(but the authors are not certain that this approach would work).
$\mathsf {GR}^\omega $
(but the authors are not certain that this approach would work).
Question. Does
![]() $\mathsf {FS}\hspace {-4pt}\restriction {} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
interpret
$\mathsf {FS}\hspace {-4pt}\restriction {} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
interpret
![]() $\mathsf {MS}(\mathcal {L}_{\iota , \mathsf {self}}) + \textsf {Self-Perception}$
?
$\mathsf {MS}(\mathcal {L}_{\iota , \mathsf {self}}) + \textsf {Self-Perception}$
?
Remark. There is another proof of the above theorem that utilizes the fine-grained result at the end of the proof of the Main Lemma. That technique only works when the theory S of the Main Lemma is finitely axiomatized (as here where
![]() $S = \{\textsf {Self-Perception}\}$
). But the technique used in the above proof works also for non-finitely axiomatized S.
$S = \{\textsf {Self-Perception}\}$
). But the technique used in the above proof works also for non-finitely axiomatized S.
Remark. Note the contrast that
![]() $\mathsf {CM}$
includes
$\mathsf {CM}$
includes
![]() $\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
while
$\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}) + \mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
while
![]() $\mathsf {GR}^\omega $
only includes
$\mathsf {GR}^\omega $
only includes
![]() $\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
. The essential reason why
$\mathsf {ZF} + \mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
. The essential reason why
![]() $\mathsf {GR}^\omega $
interprets
$\mathsf {GR}^\omega $
interprets
![]() $\mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
is that the interpretations
$\mathsf {Rep}(\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}})$
is that the interpretations
![]() $\mathcal {I}_{\underline {n}}$
in the above proof map
$\mathcal {I}_{\underline {n}}$
in the above proof map
![]() $\mathsf {Mod}$
and
$\mathsf {Mod}$
and
![]() $\mathsf {Uni}$
to the
$\mathsf {Uni}$
to the
![]() $\mathcal {L}$
-formulas
$\mathcal {L}$
-formulas
![]() $\mathrm {Mod}_{\underline {n}}$
and
$\mathrm {Mod}_{\underline {n}}$
and
![]() $\mathrm {Uni}_{\underline {n}}$
, respectively.
$\mathrm {Uni}_{\underline {n}}$
, respectively.
In light of Theorems 5.6 and 5.7, the authors ask:
Question. Is it the case that
![]() $\mathsf {GR}^\omega \equiv _{\mathcal {L}} \mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf { Self-Perception}$
? If not, what is the precise consistency strength of
$\mathsf {GR}^\omega \equiv _{\mathcal {L}} \mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf { Self-Perception}$
? If not, what is the precise consistency strength of
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
?
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
?
The fact that the extended schema
![]() $\mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
in
$\mathsf {Sep}(\mathcal {L}_{\mathsf {Sat}})$
in
![]() $\mathsf {GR}^\omega $
was only used to obtain the set of true sentences, suggests a negative answer;
$\mathsf {GR}^\omega $
was only used to obtain the set of true sentences, suggests a negative answer;
![]() $\mathsf {GR}^\omega $
may have strictly higher consistency strength than
$\mathsf {GR}^\omega $
may have strictly higher consistency strength than
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
.
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception}$
.
6 Case studies
This section examines how the framework introduced above can be applied to two rather different conceptions of the set-theoretic multiverse.
6.1 Multiverse conceptions of arithmetical absoluteness
One may feel confident in adopting a universe view on arithmetic, appealing to the general acceptance of an intended model consisting of the finite ordinals, while having a multiverse view of set theory, where agreement on an intended model is lacking. This subsection therefore explores how the techniques of this paper may be applied to a conception of the multiverse where arithmetic is more or less fixed throughout the universes.
Let
![]() $\mathcal {L}^{\mathsf {PA}}$
be the language of arithmetic, and let
$\mathcal {L}^{\mathsf {PA}}$
be the language of arithmetic, and let
![]() $\Sigma _n^{\mathsf {PA}}$
be the usual complexity hierarchy of arithmetic formulas over
$\Sigma _n^{\mathsf {PA}}$
be the usual complexity hierarchy of arithmetic formulas over
![]() $\mathsf {PA}$
. Given
$\mathsf {PA}$
. Given
![]() $\phi \in \mathcal {L}^{\mathsf {PA}}$
,
$\phi \in \mathcal {L}^{\mathsf {PA}}$
,
![]() $\phi ^{\mathbb {N}}$
denotes the corresponding
$\phi ^{\mathbb {N}}$
denotes the corresponding
![]() $\mathcal {L}$
-formula obtained by restricting the quantifiers to
$\mathcal {L}$
-formula obtained by restricting the quantifiers to
![]() $\mathbb {N}$
. Figure 3 exhibits axioms, of increasing strength, expressing the absoluteness of arithmetic. The strongest of these is Arithmetic Absoluteness, which expresses that the bounded quantifier “
$\mathbb {N}$
. Figure 3 exhibits axioms, of increasing strength, expressing the absoluteness of arithmetic. The strongest of these is Arithmetic Absoluteness, which expresses that the bounded quantifier “
![]() $\forall x \in \mathbb {N}$
” commutes with the
$\forall x \in \mathbb {N}$
” commutes with the
![]() $\mathsf {Mod}$
-relation, for the untyped language
$\mathsf {Mod}$
-relation, for the untyped language
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
.
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
.

Fig. 3 Axioms of Arithmetic Absoluteness.
Proposition 6.1.
![]() $\mathsf {CM}^- + \textsf {Arithmetic Compositionality} \vdash \textsf {Arithmetic Absoluteness}$
.
$\mathsf {CM}^- + \textsf {Arithmetic Compositionality} \vdash \textsf {Arithmetic Absoluteness}$
.
Proof. Let
![]() $\sigma \in \mathrm {Sent}(\mathcal {L}^{\mathsf {PA}})$
, such that
$\sigma \in \mathrm {Sent}(\mathcal {L}^{\mathsf {PA}})$
, such that
![]() $\sigma ^{\mathbb {N}}$
holds. Let
$\sigma ^{\mathbb {N}}$
holds. Let
![]() $\mathcal {U} \in \mathsf {Uni}$
. We show by induction on the syntactic structure that
$\mathcal {U} \in \mathsf {Uni}$
. We show by induction on the syntactic structure that
![]() $\mathsf {Mod}(\mathcal {U}, \ulcorner \sigma ^{\mathbb {N}} \urcorner ) \leftrightarrow \sigma ^{\mathbb {N}}$
. For atomic sentences it follows from that arithmetic equations are decidable. For the propositional connectives, the induction step follows from the axioms of the form
$\mathsf {Mod}(\mathcal {U}, \ulcorner \sigma ^{\mathbb {N}} \urcorner ) \leftrightarrow \sigma ^{\mathbb {N}}$
. For atomic sentences it follows from that arithmetic equations are decidable. For the propositional connectives, the induction step follows from the axioms of the form
![]() $\mathsf {CM}_-$
; let us look at
$\mathsf {CM}_-$
; let us look at
![]() $\sigma ^{\mathbb {N}} \equiv \neg \phi $
for example:
$\sigma ^{\mathbb {N}} \equiv \neg \phi $
for example:
The first equivalence holds by
![]() $\mathsf {CM}_\neg $
and the second by the induction hypothesis. For the quantifier case, suppose that
$\mathsf {CM}_\neg $
and the second by the induction hypothesis. For the quantifier case, suppose that
![]() $\sigma ^{\mathbb {N}} \equiv \forall x \in \mathbb {N} \hspace {2pt} \phi (x)$
. We calculate:
$\sigma ^{\mathbb {N}} \equiv \forall x \in \mathbb {N} \hspace {2pt} \phi (x)$
. We calculate:
The first equivalence holds by Arithmetic Compositionality, the second by the induction hypothesis, and the third by the fact that for all
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\mathbb {N} \models n = \underline {n}$
.□
$\mathbb {N} \models n = \underline {n}$
.□
The following proposition shows the reflective power of Arithmetic Absoluteness, and exhibits a scenario where
![]() $\mathsf {CONEC}$
is useful.
$\mathsf {CONEC}$
is useful.
Proposition 6.2.
![]() $\mathsf {CM} + \Sigma ^{\mathsf {PA}}_1\textsf {-Absoluteness} +\mathsf {CONEC} \vdash \mathsf {R}^{\omega ^{\mathrm {CK}}_1}$
.
$\mathsf {CM} + \Sigma ^{\mathsf {PA}}_1\textsf {-Absoluteness} +\mathsf {CONEC} \vdash \mathsf {R}^{\omega ^{\mathrm {CK}}_1}$
.
Proof. By
![]() $\mathsf {CONEC}$
it suffices to prove
$\mathsf {CONEC}$
it suffices to prove
![]() $\mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\omega ^{\mathrm {CK}}_1})$
. Naturally, we do so by transfinite induction. The base case follows from
$\mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\omega ^{\mathrm {CK}}_1})$
. Naturally, we do so by transfinite induction. The base case follows from
![]() $\textsf {Multiverse}_{\mathsf {ZF}}$
, an axiom of
$\textsf {Multiverse}_{\mathsf {ZF}}$
, an axiom of
![]() $\mathsf {CM}$
. For the successor case, assume that
$\mathsf {CM}$
. For the successor case, assume that
![]() $\mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha )$
for some
$\mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha )$
for some
![]() $\alpha < \omega ^{\mathrm {CK}}_1$
. Suppose
$\alpha < \omega ^{\mathrm {CK}}_1$
. Suppose
![]() $\mathcal {U} \in \mathsf {Uni}$
, let
$\mathcal {U} \in \mathsf {Uni}$
, let
![]() $\sigma \in \mathcal {L}$
and assume that
$\sigma \in \mathcal {L}$
and assume that
![]() $\mathsf {Mod}(\mathcal {U}, \ulcorner \Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha }(\sigma ) \urcorner )$
. Since
$\mathsf {Mod}(\mathcal {U}, \ulcorner \Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha }(\sigma ) \urcorner )$
. Since
![]() $\alpha $
is recursive,
$\alpha $
is recursive,
![]() $\Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha }$
is
$\Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha }$
is
![]() $\Sigma ^0_1$
, so by
$\Sigma ^0_1$
, so by
![]() $\Sigma ^{\mathsf {PA}}_1$
-Absoluteness, we have
$\Sigma ^{\mathsf {PA}}_1$
-Absoluteness, we have
![]() $\Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha }(\sigma )$
. It now follows from
$\Pr _{\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha }(\sigma )$
. It now follows from
![]() $\mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha )$
and the Soundness Lemma that
$\mathsf {Tr}^\Box (\underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^\alpha )$
and the Soundness Lemma that
![]() $\mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner )$
. So by
$\mathsf {Mod}(\mathcal {U}, \ulcorner \sigma \urcorner )$
. So by
![]() $\mathsf {CM}_\rightarrow $
, we have
$\mathsf {CM}_\rightarrow $
, we have
![]() $\mathsf {Mod}(\mathcal {U}, \underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\alpha +1})$
, as desired. The limit case is immediate from the definition of
$\mathsf {Mod}(\mathcal {U}, \underset {\substack {\\[-9.5pt]\mbox {.}}}{\mathsf {R}}^{\alpha +1})$
, as desired. The limit case is immediate from the definition of
![]() $\mathsf {R}^\alpha $
.□
$\mathsf {R}^\alpha $
.□
Remark. Note that the above proof argues model-theoretically on an arbitrary universe. But even though
![]() $\mathsf {CM} + \Sigma ^{\mathsf {PA}}_1\textsf {-Absoluteness} +\mathsf {CONEC}$
proves a fair amount of reflection, it is not clear to the authors whether it proves that there is a universe (Non-Triviality).
$\mathsf {CM} + \Sigma ^{\mathsf {PA}}_1\textsf {-Absoluteness} +\mathsf {CONEC}$
proves a fair amount of reflection, it is not clear to the authors whether it proves that there is a universe (Non-Triviality).
This section raises questions about the consistency (strength) of combinations of Copernican multiverse theories and axioms of arithmetic absoluteness, in particular:
Question. Is
![]() $\mathsf {CM} + \Sigma ^{\mathsf {PA}}_1\textsf {-Absoluteness} +\mathsf {CONEC}\ \text {consistent relative to }\mathsf {R}^{\omega ^{\mathrm {CK}}_1}$
?
$\mathsf {CM} + \Sigma ^{\mathsf {PA}}_1\textsf {-Absoluteness} +\mathsf {CONEC}\ \text {consistent relative to }\mathsf {R}^{\omega ^{\mathrm {CK}}_1}$
?
Question. Is
![]() $\mathsf {CM}^-(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception} + \textsf {Arithmetic Compositionality}$
consistent?
$\mathsf {CM}^-(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \textsf {Self-Perception} + \textsf {Arithmetic Compositionality}$
consistent?
The following proposition may be viewed as a partial answer to the second question, but the authors do not consider it to suggest an ultimately negative answer:
Proposition 6.3. The system
![]() $\mathsf {CM}^- + \mathsf {NEC} + \textsf {Arithmetic Compositionality} + \textsf {Non-Triviality}$
is
$\mathsf {CM}^- + \mathsf {NEC} + \textsf {Arithmetic Compositionality} + \textsf {Non-Triviality}$
is
![]() $\omega $
-inconsistent.
$\omega $
-inconsistent.
Proof. This is a corollary of McGee’s paradox, see [Reference McGee15].□
6.2 The Hamkins multiverse
Hamkins [Reference Hamkins12] introduced a conception of the set-theoretic multiverse, which informally is based on four over-arching principles:
-
1. The multiverse is a non-empty collection of models of
 $\mathsf {ZFC}$
.
$\mathsf {ZFC}$
. -
2. The multiverse is closed under the usual techniques for constructing models of set theory from other models of set theory, such as forcing extensions and inner models.
-
3. Every universe is countable and
 $\omega $
-non-standard from the perspective of another universe.
$\omega $
-non-standard from the perspective of another universe. -
4. The multiverse is closed under iterating large cardinal embeddings backward.
Definition 1.1 in [Reference Gitman and Hamkins7, pp. 475–476] gives succinct formulations of axioms encapsulating this conception. The third (and possibly the fourth) principle is more controversial than the first two. For example, the Well-foundedness Mirage axiom states that for every universe
![]() $\mathcal {U}$
there is a universe
$\mathcal {U}$
there is a universe
![]() $\mathcal {V}$
which thinks
$\mathcal {V}$
which thinks
![]() $\mathcal {U}$
is
$\mathcal {U}$
is
![]() $\omega $
-non-standard.
$\omega $
-non-standard.
Philosophical arguments in support for the axioms are provided in [Reference Hamkins12, sec. Reference Gupta9]; and a model of them is constructed by [Reference Gitman and Hamkins7], essentially taking the multiverse to consist of the countable recursively saturated models of
![]() $\mathsf {ZFC}$
. We call this the Gitman–Hamkins model of the multiverse.
$\mathsf {ZFC}$
. We call this the Gitman–Hamkins model of the multiverse.
Gitman and Hamkins [Reference Gitman and Hamkins7] consider a weak and strong form of Well-foundedness Mirage. In the terminology of this paper, these are formally stated as follows:
 $$ \begin{align*} \begin{array}{ll} \textsf{WM}_{\textsf{weak}} & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \exists \mathcal{V} \in \mathsf{Uni}\hspace{2pt} \exists u \in \mathcal{V} \hspace{2pt} \big( u_{\mathcal{V}} = \mathcal{U} \wedge {} \\ & \quad {} \wedge \mathcal{V} \models \text{“}u\ \text{is}\ \omega\text{-non-standard”}\big), \\ \textsf{WM}_{\textsf{strong}} & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \exists \mathcal{V} \in \mathsf{Uni}\hspace{2pt} \exists u \in \mathcal{V} \hspace{2pt} \big( u_{\mathcal{V}} = \mathcal{U} \wedge {} \\ & \quad {} \wedge \mathcal{V} \models \text{“}u\ \text{is an } \omega\text{-non-standard model of }\mathsf{ZFC}\text{”}\big). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \textsf{WM}_{\textsf{weak}} & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \exists \mathcal{V} \in \mathsf{Uni}\hspace{2pt} \exists u \in \mathcal{V} \hspace{2pt} \big( u_{\mathcal{V}} = \mathcal{U} \wedge {} \\ & \quad {} \wedge \mathcal{V} \models \text{“}u\ \text{is}\ \omega\text{-non-standard”}\big), \\ \textsf{WM}_{\textsf{strong}} & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \exists \mathcal{V} \in \mathsf{Uni}\hspace{2pt} \exists u \in \mathcal{V} \hspace{2pt} \big( u_{\mathcal{V}} = \mathcal{U} \wedge {} \\ & \quad {} \wedge \mathcal{V} \models \text{“}u\ \text{is an } \omega\text{-non-standard model of }\mathsf{ZFC}\text{”}\big). \end{array} \end{align*} $$
The distinction between the axioms is discussed in [Reference Gitman and Hamkins7, pp. 479–480], where a reflection assumption is introduced to ensure that the stronger axiom gets validated in the model. Their multiverse conception is flat in the sense that it does not consider the universes as themselves being models of the multiverse axioms. However, the move from
![]() $\textsf {WM}_{\textsf {weak}}$
to
$\textsf {WM}_{\textsf {weak}}$
to
![]() $\textsf {WM}_{\textsf {strong}}$
may naturally be viewed as a step in that direction. Accordingly, we may reformulate Well-founded Mirage in
$\textsf {WM}_{\textsf {strong}}$
may naturally be viewed as a step in that direction. Accordingly, we may reformulate Well-founded Mirage in
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
as:
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
as:
 $$ \begin{align*} \begin{array}{ll} \textsf{WM} & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \exists \mathcal{V} \in \mathsf{Uni}\hspace{2pt} \exists u \in \mathcal{V} \hspace{2pt} \big( u_{\mathcal{V}} = \mathcal{U} \wedge {} \\ & \quad {} \wedge \mathsf{Mod}(\mathcal{V}, \text{“}u\text{ is an }\omega\text{-non-standard model in }\mathbf{Uni}\text{”}) \big). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ll} \textsf{WM} & \forall \mathcal{U} \in \mathsf{Uni}\hspace{2pt} \exists \mathcal{V} \in \mathsf{Uni}\hspace{2pt} \exists u \in \mathcal{V} \hspace{2pt} \big( u_{\mathcal{V}} = \mathcal{U} \wedge {} \\ & \quad {} \wedge \mathsf{Mod}(\mathcal{V}, \text{“}u\text{ is an }\omega\text{-non-standard model in }\mathbf{Uni}\text{”}) \big). \end{array} \end{align*} $$
Informally speaking this says not only “for every universe
![]() $\mathcal {U}$
there is a universe
$\mathcal {U}$
there is a universe
![]() $\mathcal {V}$
that thinks that
$\mathcal {V}$
that thinks that
![]() $\mathcal {U}$
is
$\mathcal {U}$
is
![]() $\omega $
-non-standard,” but also “
$\omega $
-non-standard,” but also “
![]() $\mathcal {V}$
thinks that
$\mathcal {V}$
thinks that
![]() $\mathcal {U}$
is a universe.” Note that over
$\mathcal {U}$
is a universe.” Note that over
![]() $\mathsf {CM} + \textsf {Choice} + \mathsf {NEC}$
,Footnote
18
we get
$\mathsf {CM} + \textsf {Choice} + \mathsf {NEC}$
,Footnote
18
we get
![]() $\textsf { WM}_{\textsf {strong}}$
from
$\textsf { WM}_{\textsf {strong}}$
from
![]() $\textsf {WM}$
, and also iterated forms of
$\textsf {WM}$
, and also iterated forms of
![]() $\textsf {WM}$
, starting with
$\textsf {WM}$
, starting with
![]() $\forall \mathcal {W} \in \mathsf {Uni}\hspace {2pt} \mathsf {Mod}(\mathcal {W}, \textsf {WM})$
. The authors take this to be a natural way for Well-founded Mirage to manifest in the multiverse of sets. The analogous modification can also be made to the Countability axiom in Definition 1.1 of [Reference Gitman and Hamkins7].
$\forall \mathcal {W} \in \mathsf {Uni}\hspace {2pt} \mathsf {Mod}(\mathcal {W}, \textsf {WM})$
. The authors take this to be a natural way for Well-founded Mirage to manifest in the multiverse of sets. The analogous modification can also be made to the Countability axiom in Definition 1.1 of [Reference Gitman and Hamkins7].
We write
![]() $\mathsf {HM}$
(the Hamkins Multiverse) for the
$\mathsf {HM}$
(the Hamkins Multiverse) for the
![]() $\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-theory obtained by extending
$\mathcal {L}_{\mathsf {Uni}, \mathsf {Mod}}$
-theory obtained by extending
![]() $\mathsf {CM}$
with the axioms of Definition 1.1 in [Reference Gitman and Hamkins7] reformulated so that
$\mathsf {CM}$
with the axioms of Definition 1.1 in [Reference Gitman and Hamkins7] reformulated so that
![]() $\models $
is replaced by
$\models $
is replaced by
![]() $\mathsf {Mod}$
and the Well-founded Mirage and Countability axioms are modified as above. In general, it is natural to add the closure condition
$\mathsf {Mod}$
and the Well-founded Mirage and Countability axioms are modified as above. In general, it is natural to add the closure condition
![]() $\mathsf {NEC}$
to this system, since that gives us a Copernican conception which ensures that the background universe does not have a privileged point of outlook over the multiverse. In particular, this yields a natural strengthening of Well-founded Mirage (and Countability), as explained in the previous paragraph. Moreover, the techniques used to validate Self-Perception in this paper are closely related to the validation of Well-founded Mirage by [Reference Gitman and Hamkins7]. Therefore, the authors champion
$\mathsf {NEC}$
to this system, since that gives us a Copernican conception which ensures that the background universe does not have a privileged point of outlook over the multiverse. In particular, this yields a natural strengthening of Well-founded Mirage (and Countability), as explained in the previous paragraph. Moreover, the techniques used to validate Self-Perception in this paper are closely related to the validation of Well-founded Mirage by [Reference Gitman and Hamkins7]. Therefore, the authors champion
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {HM} + \textsf {Self-Perception}$
as a theory of the multiverse.
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {HM} + \textsf {Self-Perception}$
as a theory of the multiverse.
Note that the choice of
![]() $\mathbf {Uni}_n$
in the proof of Theorem 5.7 is the collection of countable recursively saturated models, just as in the Gitman–Hamkins model of the multiverse. A plausible approach to proving the consistency of the above theory is therefore to use the construction from the proof of Theorem 5.7, setting up the revision parameters
$\mathbf {Uni}_n$
in the proof of Theorem 5.7 is the collection of countable recursively saturated models, just as in the Gitman–Hamkins model of the multiverse. A plausible approach to proving the consistency of the above theory is therefore to use the construction from the proof of Theorem 5.7, setting up the revision parameters
![]() $\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
so that for each
$\mathrm {T}, \mathrm {Uni}, \mathrm {Mod}_0$
so that for each
![]() $n \in \mathbb {N}$
:
$n \in \mathbb {N}$
:
 $$ \begin{align*} \mathbf{T}_n &= \mathsf{SP}^n(\mathsf{ZFC}), \\ \mathbf{Uni}_{n+1} &= \{\mathcal{U} \mid \mathcal{U} \models \mathbf{T}_{n} \wedge \mathcal{U}\hspace{-4pt}\restriction_{\mathcal{L}} \in \mathbf{crsm}\}. \end{align*} $$
$$ \begin{align*} \mathbf{T}_n &= \mathsf{SP}^n(\mathsf{ZFC}), \\ \mathbf{Uni}_{n+1} &= \{\mathcal{U} \mid \mathcal{U} \models \mathbf{T}_{n} \wedge \mathcal{U}\hspace{-4pt}\restriction_{\mathcal{L}} \in \mathbf{crsm}\}. \end{align*} $$
Conjecture .
![]() $\mathsf {GR}^\omega (\mathsf {ZFC})$
interprets
$\mathsf {GR}^\omega (\mathsf {ZFC})$
interprets
![]() $\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \mathsf {HM} + \textsf { Self-Perception}$
.
$\mathsf {CM}(\mathcal {L}_{\iota , \mathsf {self}}) + \mathsf {NEC} + \mathsf {HM} + \textsf { Self-Perception}$
.
Addressing this conjecture falls outside the scope of this paper. What needs to be done is essentially to verify that the proof of the Main Theorem by [Reference Gitman and Hamkins7] generalizes from models of
![]() $\mathsf {ZFC}$
to models of
$\mathsf {ZFC}$
to models of
![]() $\mathsf {SP}^n(\mathsf {ZFC})$
.
$\mathsf {SP}^n(\mathsf {ZFC})$
.
7 Conclusion
We have developed a framework of satisfaction for the multiverse of set theory, with two sides: A revision-semantic construction of an increasingly adequate definition of truth-in-a-universe, and a family of axiomatic theories validated by the revision construction. We have shown how the construction can be adjusted, by tuning the revision parameters, in order to validate various multiverse axioms.
The basic theory of satisfaction for the multiverse is
![]() $\mathsf {CM}$
, which extends
$\mathsf {CM}$
, which extends
![]() $\mathsf {ZF}$
with axioms expressing that truth-in-a-universe is compositional with respect to the logical connectives and quantifiers. Adding the deductive rule
$\mathsf {ZF}$
with axioms expressing that truth-in-a-universe is compositional with respect to the logical connectives and quantifiers. Adding the deductive rule
![]() $\mathsf {NEC}$
yields a system with the closure condition that whatever is provable in the multiverse theory also provably holds in each universe. So such a system respects the Copernican Principle that the background universe should not have a privileged point of outlook over the multiverse. Adding also the dual principle of
$\mathsf {NEC}$
yields a system with the closure condition that whatever is provable in the multiverse theory also provably holds in each universe. So such a system respects the Copernican Principle that the background universe should not have a privileged point of outlook over the multiverse. Adding also the dual principle of
![]() $\mathsf {CONEC}$
yields the system
$\mathsf {CONEC}$
yields the system
![]() $\mathsf {MS}$
.
$\mathsf {MS}$
.
![]() $\mathsf {MS}$
is in a sense analogous to the Friedman–Sheard theory of truth (
$\mathsf {MS}$
is in a sense analogous to the Friedman–Sheard theory of truth (
![]() $\mathsf {FS}$
), but in Theorem 4.8 we saw that, unlike
$\mathsf {FS}$
), but in Theorem 4.8 we saw that, unlike
![]() $\mathsf {FS}$
, it is conservative over the base theory, under the meta-theoretic assumption that
$\mathsf {FS}$
, it is conservative over the base theory, under the meta-theoretic assumption that
![]() $\mathsf {ZF}$
is closed under the Reflection rule (which follows if
$\mathsf {ZF}$
is closed under the Reflection rule (which follows if
![]() $\mathsf {ZF}$
is
$\mathsf {ZF}$
is
![]() $\omega $
-consistent, and in particular if there is an
$\omega $
-consistent, and in particular if there is an
![]() $\omega $
-standard model of
$\omega $
-standard model of
![]() $\mathsf {ZF}$
).
$\mathsf {ZF}$
).
The choice of
![]() $\mathsf {ZF}$
as base theory for our framework is important for the axiom of
$\mathsf {ZF}$
as base theory for our framework is important for the axiom of
![]() $\textsf {Self-Perception}$
. The proof of Theorem 5.7 yields a model of
$\textsf {Self-Perception}$
. The proof of Theorem 5.7 yields a model of
![]() $\mathsf {CM}(\mathcal {L}_{\mathsf {Sat}}) + \mathsf {NEC} + \textsf {Self-Perception}$
satisfying that each universe is a countable recursively saturated model of
$\mathsf {CM}(\mathcal {L}_{\mathsf {Sat}}) + \mathsf {NEC} + \textsf {Self-Perception}$
satisfying that each universe is a countable recursively saturated model of
![]() $\mathsf {ZF}$
(under
$\mathsf {ZF}$
(under
![]() $\mathsf {Mod}$
). As far as the authors can see, both the full Separation and Replacement schemas of
$\mathsf {Mod}$
). As far as the authors can see, both the full Separation and Replacement schemas of
![]() $\mathsf {ZF}$
, as well as its Foundation axiom, are needed both for the background theory and for the internal theory of each universe, due to the application of Theorem 2.4 in the proofs of Lemmas 2.14 and 2.18. In contrast, for the weaker extensions of
$\mathsf {ZF}$
, as well as its Foundation axiom, are needed both for the background theory and for the internal theory of each universe, due to the application of Theorem 2.4 in the proofs of Lemmas 2.14 and 2.18. In contrast, for the weaker extensions of
![]() $\mathsf {CM}$
introduced in this paper, the authors do not see any need for full
$\mathsf {CM}$
introduced in this paper, the authors do not see any need for full
![]() $\mathsf {ZF}$
. For example, the authors believe that most of the results of this paper hold (with minor modifications) also when taking Mac Lane set theory,Footnote
19
or Kripke–Platek set theory with Infinity,Footnote
20
as base theory and as theory for the internal universes. Due to the close connection between Mac Lane set theory and topoi, this suggests that the framework can be adapted to give an analogous multiverse framework for topos theory.
$\mathsf {ZF}$
. For example, the authors believe that most of the results of this paper hold (with minor modifications) also when taking Mac Lane set theory,Footnote
19
or Kripke–Platek set theory with Infinity,Footnote
20
as base theory and as theory for the internal universes. Due to the close connection between Mac Lane set theory and topoi, this suggests that the framework can be adapted to give an analogous multiverse framework for topos theory.
We explored adding axioms of a reflective character, asserting that the universe of the background multiverse theory is reflected in the multiverse. Whereas Non-Triviality merely states the existence of a universe in the multiverse,
![]() $\textsf {Multiverse Reflection}$
can be viewed as expressing that for every formula in the base language that holds in the background universe, it holds in some universe.
$\textsf {Multiverse Reflection}$
can be viewed as expressing that for every formula in the base language that holds in the background universe, it holds in some universe.
![]() $\textsf {Self-Perception}$
goes as far as expressing that the background universe is isomorphic to a universe in the multiverse. These axioms were interpreted in systems of various types of iterated reflection over
$\textsf {Self-Perception}$
goes as far as expressing that the background universe is isomorphic to a universe in the multiverse. These axioms were interpreted in systems of various types of iterated reflection over
![]() $\mathsf {ZF}$
, all of which are very mild in terms of consistency strength; indeed their consistency strengths are all bounded by Morse–Kelley class theory with Global Choice (and the remark following System 5.3 indicates that they are far weaker), which in turn is far weaker than
$\mathsf {ZF}$
, all of which are very mild in terms of consistency strength; indeed their consistency strengths are all bounded by Morse–Kelley class theory with Global Choice (and the remark following System 5.3 indicates that they are far weaker), which in turn is far weaker than
![]() $\mathsf {ZFC} + \text {“there exists an inaccessible cardinal.”}$
$\mathsf {ZFC} + \text {“there exists an inaccessible cardinal.”}$
Having this framework available, the multiverse theorist can proceed to make use of its untyped relation of truth-in-a-universe. Apart from the light it sheds on the axioms above, a concrete value added, compared to the usual
![]() $\models $
-relation, is that it makes it possible to express multiverse principles that reach arbitrarily deep into the structure of universes, universes within universes, universes within universes within universes, etc. We give the final word to Tomas Tranströmer, through his poem “Romanska bågar” (translation by Robert Bly):
$\models $
-relation, is that it makes it possible to express multiverse principles that reach arbitrarily deep into the structure of universes, universes within universes, universes within universes within universes, etc. We give the final word to Tomas Tranströmer, through his poem “Romanska bågar” (translation by Robert Bly):
Inne i dig öppnar sig valv bakom valv oändligt.
Du blir aldrig färdig, och det är som det skall.
Inside you one vault after another opens endlessly.
You’ll never be complete, and that’s as it should be.
Acknowledgments
This research was supported by the Swedish Research Council (VR) [2017-05111], and by the Knut and Alice Wallenberg Foundation (KAW) [2015.0179]. The authors are grateful for the comments and suggestions of the anonymous referee, to Anton Broberg for permitting us to incorporate his argument for Lemma 5.1, and to Ali Enayat for answering our question on the relationship between Self-Perception and recursive saturation (see Section 1.1).