No CrossRef data available.
Article contents
CALCULIZING CLASSICAL INFERENTIAL EROTETIC LOGIC
Published online by Cambridge University Press: 29 June 2020
Abstract
This paper contributes to the calculization of evocation and erotetic implication as defined by Inferential Erotetic Logic (IEL). There is a straightforward approach to calculizing (propositional) erotetic implication which cannot be applied to evocation. First-order evocation is proven to be uncalculizable, i.e. there is no proof system, say FOE, such that for all
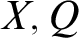 $X, Q$
: X evokes Q iff there is an FOE-proof for the evocation of Q by X. These results suggest a critique of the represented approaches to calculizing IEL. This critique is expanded into a programmatic reconsideration of the IEL-definitions of evocation and erotetic implication. From a different point of view these definitions should be seen as desiderata that may or may not play the role of a point of orientation when setting up “rules of asking.”
$X, Q$
: X evokes Q iff there is an FOE-proof for the evocation of Q by X. These results suggest a critique of the represented approaches to calculizing IEL. This critique is expanded into a programmatic reconsideration of the IEL-definitions of evocation and erotetic implication. From a different point of view these definitions should be seen as desiderata that may or may not play the role of a point of orientation when setting up “rules of asking.”
MSC classification
- Type
- Research Article
- Information
- Copyright
- © Association for Symbolic Logic, 2020



