Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T16:02:02.611Z Has data issue: false hasContentIssue false
  • English
  • Français

BELIEF REVISION IN NON-CLASSICAL LOGICS

Published online by Cambridge University Press:  01 October 2008

DOV GABBAY ,
ODINALDO RODRIGUES  and
ALESSANDRA RUSSO
DOV GABBAY*
Affiliation:
Department of Computer Science, King's College London
ODINALDO RODRIGUES*
Affiliation:
Department of Computer Science, King's College London
ALESSANDRA RUSSO*
Affiliation:
Department of Computing, Imperial College
*
*DEPARTMENT OF COMPUTER SCIENCE, KING'S COLLEGE LONDON LONDON WC2R 2LS, UK E-mail:[email protected]
†DEPARTMENT OF COMPUTER SCIENCE, KING'S COLLEGE LONDON LONDON WC2R 2LS, UK E-mail:[email protected]
‡DEPARTMENT OF COMPUTING, IMPERIAL COLLEGE, LONDON SW7 2BZ, UK E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

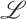In this article, we propose a belief revision approach for families of (non-classical) logics whose semantics are first-order axiomatisable. Given any such (non-classical) logic , the approach enables the definition of belief revision operators for 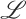, in terms of a belief revision operation satisfying the postulates for revision theory proposed by Alchourrón, Gärdenfors and Makinson (AGM revision, Alchourrón et al. (1985)). The approach is illustrated by considering the modal logic K, Belnap's four-valued logic, and Łukasiewicz's many-valued logic. In addition, we present a general methodology to translate algebraic logics into classical logic. For the examples provided, we analyse in what circumstances the properties of the AGM revision are preserved and discuss the advantages of the approach from both theoretical and practical viewpoints.

Type
Research Article
Information
The Review of Symbolic Logic , Volume 1 , Issue 3 , October 2008 , pp. 267 - 304
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Alchourrón, C. E., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: partial meet contraction and revision functions. Journal of Symbolic Logic, 50(2), 510–530.Google Scholar
Anderson, A. R., Belnap, N. D., & Dunn, J. M. (1992). A Useful Four-Valued Logic: How a Computer Should Think[Section 81 of Anderson, A.R., and Belnap, N.D., Jr., and Dunn, J.M., et al. Entailment, vol. II, pp. 506–541]. Princeton, NJ: Princeton University Press.Google Scholar
Belnap, N. (1977a). How a computer should think. In Ryle, G., editor, Contemporary Aspects of Philosophy. Stocksfield: Oriel Press, pp. 30–56.Google Scholar
Belnap, N. (1977b). A useful four-valued logic. In Dunn, J. M. and Epstein, G., editors, Modern Uses of Multiple-Valued Logic. Stocksfield: Reidel, pp. 8–37.Google Scholar
Broda, K., Russo, A., & Gabbay, D. (2000). Discovering world with fuzzy logic: perspectives and approaches to the formalisation of human-consistent logical systems. In Novak, V., and Perf, I., editors, A Unified Compilation Style Labelled Deductive Systems for Modal, Substructural and Fuzzy Logic. Berlin, Germany: Springer-Verlag, pp. 495–547.Google Scholar
Chellas, B. F. (1980). Modal Logic: an Introduction. Cambridge, UK: Cambridge University Press.Google Scholar
Darwiche, A., & Pearl, J. (1996). On the logic of iterated belief revision. Technical Report R-202. Cognitive Science Laboratory, Computer Science Department, University of California, Los Angeles, CA.Google Scholar
Darwiche, A., & Pearl, J. (1997). On the logic of iterated belief revision. Artificial Intelligence, 89, 1–29.Google Scholar
Fuhrmann, A. (1991). Theory contraction through base contraction. Journal of Philosophical Logic, 20(2), 175–203. DOI 10.1007/BF00284974.CrossRefGoogle Scholar
Gabbay, D. M., & Maksimova, L. (2005). Interpolation and Definability. Modal and Intuitionistic Logics, vol. 1. Oxford, UK: Oxford Science Publications. ISBN 0-19-851174-4.CrossRefGoogle Scholar
Gabbay, D. M., Pigozzi, G., & Rodrigues, O. (2006). Belief revision, belief merging and voting. In Bonanno, G., van der Hoek, W., and Wooldridge, M., editors, Proceedings of the Seventh Conference on Logic and the Foundations of Games and Decision Theory (LOFT06). Liverpool, UK: University of Liverpool, pp. 71–78.Google Scholar
Gabbay, D., Rodrigues, O., & Russo, A. (2000). Information, uncertainty, fusion. In Yager, R. R., Zadeh, L. A., and Bouchon-Meunier, B., editors, Revision by Translation. Norwell, MA: Kluwer Academic Publishers, pp. 3–31. ISBN: 0-7923-8590-X.Google Scholar
Gärdenfors, P. (1988). Knowledge in Flux: Modeling the Dynamics of Epistemic states. A Bradford Book. Cambridge, MA: The MIT Press.Google Scholar
Katsuno, H., & Mendelzon, A. O. (1991). Propositional knowledge base revision and minimal change. Artificial Intelligence, 52, 263–294.CrossRefGoogle Scholar
Martins, J. P., & Shapiro, S. C. (1988). A model for belief revision. Artificial Intelligence, 35(1), 25–79.Google Scholar
Ohlbach, H. J. (1991). Semantics-based translations methods for modal logics. Journal of Logic and Computation, 1(5), 691–746.Google Scholar
Priest, G. (2001). Paraconsistent belief revision. Theoria, 67, 214–228.CrossRefGoogle Scholar
Restall, G., & Slaney, J. (1995). Realistic belief revision. In De Glas, M., and Pawlak, Z., editors, Wocfai 95: Proceedings of the Second World Conference on the Fundamentals of Artificial Intelligence, Angkor, July 1995. Paris, France: Angkor, pp. 67–378. ISBN 2-87892-009-0.Google Scholar
Shapiro, S. C. (1992). Relevance logic in computer science[Section 83 of Anderson, A.R., and Belnap, N.D., Jr., and Dunn, J.M., et al. Entailment, vol. II, pp. 553–563]. Princeton, NJ: Princeton University Press.Google Scholar
Tanaka, K. (1997). What Does Paraconsistency Do? Prague, Czech Republic: Filosofia. The Case of Belief Revision. The Logica Yearbook.Google Scholar