Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T03:35:15.516Z Has data issue: false hasContentIssue false
  • English
  • Français

ARITHMETICAL INTERPRETATIONS AND KRIPKE FRAMES OF PREDICATE MODAL LOGIC OF PROVABILITY

Published online by Cambridge University Press:  12 October 2012

TAISHI KURAHASHI
TAISHI KURAHASHI*
Affiliation:
Graduate School of System Informatics, Kobe University
*
*GRADUATE SCHOOL OF SYSTEM INFORMATICS KOBE UNIVERSITY 1-1 ROKKODAI, NADA, KOBE, JAPAN. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Solovay proved the arithmetical completeness theorem for the system GL of propositional modal logic of provability. Montagna proved that this completeness does not hold for a natural extension QGL of GL to the predicate modal logic. Let Th(QGL) be the set of all theorems of QGL, Fr(QGL) be the set of all formulas valid in all transitive and conversely well-founded Kripke frames, and let PL(T) be the set of all predicate modal formulas provable in Tfor any arithmetical interpretation. Montagna’s results are described as Th(QGL) ⊊ (Fr(QGL), PL(PA) ⊈ Fr(QGL), and Th(QGL) ⊊ PL(PA).

In this paper, we prove the following three theorems: (1) Fr(QGL) ⊈ PL(T) for any Σ1-sound recursively enumerable extension T of I Σ1, (2) PL(T) ⊈ Fr(QGL) for any recursively enumerable 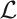A-theory T extending I Σ1, and (3) Th(QGL) ⊊ Fr(QGL) ∩ PL(T) for any recursively enumerable 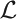A-theory T extending I Σ2.

To prove these theorems, we use iterated consistency assertions and nonstandard models of arithmetic, and we improve Artemov’s lemma which is used to prove Vardanyan’s theorem on the Π02-completeness of PL(T).

Type
Research Article
Information
The Review of Symbolic Logic , Volume 6 , Issue 1 , March 2013 , pp. 129 - 146
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Artemov, S. N. (1985). Nonarithmeticity of truth predicate logics of provability. Doklady Akademii Nauk SSSR, 284(2), 270–271(in Russian).Google Scholar
Artemov, S. N., & Japaridze, G. (1990). Finite kripke models and predicate logics of provability. The Journal of Symbolic Logic, 55(3), 1090–1098.Google Scholar
Beklemishev, L. D. (1997). Induction rules, reflection principles, and provably recursive functions. Annals of Pure and Applied Logic, 85(3), 193–242.Google Scholar
Boolos, G. (1993). The Logic of Provability. Cambridge, NY: Cambridge University Press.Google Scholar
Boolos, G., & Sambin, G. (1991). Provability: The emergence of a mathematical modality. Studia Logica, 50(1), 1–23.Google Scholar
de Jonge, M. (2005). Vardanyan’s Theorem for Extensions of IΣ1. Logic Group Preprint Series 241, Department of Philosophy, Utrecht University, Heidelberglaan8, 3584 CS Utrecht. Available from:http://preprints.phil.uu.nl/lgps/.Google Scholar
Feferman, S. (1962). Transfinite recursive progressions of axiomatic theories. The Journal of Symbolic Logic, 27(3), 259–316.Google Scholar
Hájek, P., & Pudlák, P. (1993). Metamathematics of First-Order Arithmetic. Perspectives in Mathematical Logic. Berlin: Springer-Verlag.Google Scholar
Lindström, P. (1997). Aspects of Incompleteness, Vol. 10 of Lecture Notes in Logic. Berlin: Springer-Verlag.Google Scholar
Montagna, F. (1984). The predicate modal logic of provability. Notre Dame Journal of Formal Logic, 25(2), 179–189.CrossRefGoogle Scholar
Segerberg, K. (1971). An Essay in Classical Modal Logic. Filosofiska Föreningen och Filosofiska Institutionen vid Uppsala Universitet.Google Scholar
Smoryński, C. (1985). Self-reference and Modal Logic. Universitext. New York: Springer-Verlag.Google Scholar
Solovay, R. M. (1976). Provability interpretations of modal logic. Israel Journal of Mathematics, 25(3–4), 287–304.CrossRefGoogle Scholar
Turing, A. M. (1939). Systems of logic based on ordinals. Proceedings of the London Mathematical Society, 45(2), 161–228.Google Scholar
Vardanyan, V. A. (1986). Arithmetic complexity of provability predicate logics and their fragments. Doklady Akademii Nauk SSSR, 288(1), 11–14(in Russian).Google Scholar
Visser, A., & de Jonge, M. (2006). No escape from Vardanyan’s theorem. Archive for Mathematical Logic, 45(5), 539–554.Google Scholar