Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T07:04:37.013Z Has data issue: false hasContentIssue false
  • English
  • Français

ANOTHER ARITHMETIC OF THE EVEN AND THE ODD

Published online by Cambridge University Press:  06 April 2018

CELIA SCHACHT
CELIA SCHACHT*
Affiliation:
School of Mathematical and Natural Sciences, Arizona State University
*
*SCHOOL OF MATHEMATICAL AND NATURAL SCIENCES ARIZONA STATE UNIVERSITY - WEST CAMPUS P.O. Box 37100 Phoenix, AZ 85069-7100, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This article presents an axiom system for an arithmetic of the even and the odd, one that is stronger than those discussed in Pambuccian (2016) and Menn & Pambuccian (2016). It consists of universal sentences in a language extending the usual one with 0, 1, +, ·, <, – with the integer part of the half function 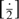$[{ \cdot \over 2}]$, and two unary operation symbols.

Keywords

03F30weak arithmeticsPythagorean arithmeticeven and odd arithmetic.
Type
Research Article
Information
The Review of Symbolic Logic , Volume 11 , Issue 3 , September 2018 , pp. 604 - 608
Copyright
Copyright © Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Kaye, R. (1991). Models of Peano Arithmetic. Oxford: Oxford University Press.Google Scholar
Menn, S. & Pambuccian, V. (2016). Addenda et corrigenda to “The arithmetic of the even and the odd.” Review of Symbolic Logic, 9, 638–640.CrossRefGoogle Scholar
Pambuccian, V. (2016). The arithmetic of the even and the odd. Review of Symbolic Logic, 9, 359–369.CrossRefGoogle Scholar
Pambuccian, V. (2018). A problem in Pythagorean Arithmetic. Notre Dame Journal of Formal Logic, 59, 197–204.CrossRefGoogle Scholar