Article contents
WHAT IS A RULE OF INFERENCE?
Published online by Cambridge University Press: 21 December 2020
Abstract
We explore the problems that confront any attempt to explain or explicate exactly what a primitive logical rule of inference is, or consists in. We arrive at a proposed solution that places a surprisingly heavy load on the prospect of being able to understand and deal with specifications of rules that are essentially self-referring. That is, any rule 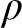 $\rho $
is to be understood via a specification that involves, embedded within it, reference to rule
$\rho $
is to be understood via a specification that involves, embedded within it, reference to rule 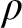 $\rho $
itself. Just how we arrive at this position is explained by reference to familiar rules as well as less familiar ones with unusual features. An inquiry of this kind is surprisingly absent from the foundations of inferentialism—the view that meanings of expressions (especially logical ones) are to be characterized by the rules of inference that govern them.
$\rho $
itself. Just how we arrive at this position is explained by reference to familiar rules as well as less familiar ones with unusual features. An inquiry of this kind is surprisingly absent from the foundations of inferentialism—the view that meanings of expressions (especially logical ones) are to be characterized by the rules of inference that govern them.
Keywords
- Type
- Research Article
- Information
- Copyright
- © Association for Symbolic Logic, 2020
References
BIBLIOGRAPHY
- 1
- Cited by



