Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-24T12:23:07.965Z Has data issue: false hasContentIssue false
  • English
  • Français

SATISFACTION CLASSES WITH APPROXIMATE DISJUNCTIVE CORRECTNESS

Part of: Proof theory and constructive mathematics Model theory

Published online by Cambridge University Press:  13 December 2024

ALI ENAYAT Open the ORCID record for ALI ENAYAT [Opens in a new window]
ALI ENAYAT*
Affiliation:
DEPARTMENT OF PHILOSOPHY, LINGUISTICS, AND THEORY OF SCIENCE UNIVERSITY OF GOTHENBURG GOTHENBURG, SWEDEN
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The seminal Krajewski–Kotlarski–Lachlan theorem (1981) states that every countable recursively saturated model of 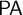$\mathsf {PA}$ (Peano arithmetic) carries a full satisfaction class. This result implies that the compositional theory of truth over 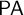$\mathsf {PA}$ commonly known as 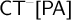$\mathsf {CT}^{-}[\mathsf {PA}]$ is conservative over 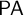$\mathsf {PA}$. In contrast, Pakhomov and Enayat (2019) showed that the addition of the so-called axiom of disjunctive correctness (that asserts that a finite disjunction is true iff one of its disjuncts is true) to 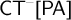$\mathsf {CT}^{-}[\mathsf {PA}]$ axiomatizes the theory of truth 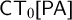$\mathsf {CT}_{0}[\mathsf {PA}]$ that was shown by Wcisło and Łełyk (2017) to be nonconservative over 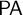$\mathsf {PA}$. The main result of this paper (Theorem 3.12) provides a foil to the Pakhomov–Enayat theorem by constructing full satisfaction classes over arbitrary countable recursively saturated models of 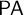$\mathsf {PA}$ that satisfy arbitrarily large approximations of disjunctive correctness. This shows that in the Pakhomov–Enayat theorem the assumption of disjunctive correctness cannot be replaced with any of its approximations.

Keywords

Peano arithmeticaxiomatic theories of truthconservativitydisjunctive correctness

MSC classification

Primary: 03C62: Models of arithmetic and set theory 03F30: First-order arithmetic and fragments
Secondary: 03F25: Relative consistency and interpretations
Type
Research Article
Information
The Review of Symbolic Logic , First View , pp. 1 - 18
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

BIBLIOGRAPHY

Abdul-Quader, A., & Łełyk, M. (2024). Pathologies in satisfaction classes. Annals of Pure and Applied Logic, 175(2), Article no. 103387, 32 pp.CrossRefGoogle Scholar
Buss, S. (1998). An introduction to proof theory . In Handbook of Proof Theory. Buss, S. R. (ed), Amsterdam: North-Holland, pp. 1–78.Google Scholar
Cieśliński, C. (2010). Deflationary truth and pathologies. The Journal of Philosophical Logic, 39, 325–337.CrossRefGoogle Scholar
Cieśliński, C. (2017). The Epistemic Lightness of Truth: Deflationism and its Logic. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Cieśliński, C. (2021). Interpreting the compositional truth predicate in models of arithmetic. Archive for Mathematical Logic, 60, 749–770.CrossRefGoogle Scholar
Cieśliński, C. (2021). On some problems with truth and satisfaction. In Trepczyński, M., editor. Philosophical Approaches to the Foundations of Logic and Mathematics. Leiden: Brill, pp. 175–192.CrossRefGoogle Scholar
Cieśliński, C., Łełyk, M., & Wcisło, B. (2023). The two halves of disjunctive correctness. Journal of Mathematical Logic , 23(2), Article no. 2250026, 28 pp.CrossRefGoogle Scholar
Enayat, A. (2023). Curious satisfaction classes. Preprint, arXiv:2308.07463 [math.LO].Google Scholar
Enayat, A., Łełyk, M., & Wcisło, B. (2020). Truth and feasible reducibility. Journal of Symbolic Logic, 85, 367–421.CrossRefGoogle Scholar
Enayat, A., & Pakhomov, F. (2019). Truth, disjunction, and induction. Archive for Mathematical Logic, 58, 753–766.CrossRefGoogle Scholar
Enayat, A., & Visser, A. (2012). Full satisfaction classes in a general setting, privately circulated manuscript.Google Scholar
Enayat, A., & Visser, A. (2015). New constructions of full satisfaction classes. In Achourioti, T., Galinon, H., Fujimoto, K., & Martínez-Fernández, J., editors. Unifying the Philosophy of Truth. New York: Springer, pp. 321–325.CrossRefGoogle Scholar
Engström, F. (2002). Satisfaction classes in nonstandard models of first-order arithmetic. Preprint, arXiv:math/0209408 [math.LO].Google Scholar
Fujimoto, K. (2022). The function of truth and the conservativeness argument. Mind, 131, 129–157.CrossRefGoogle Scholar
Hájek, P., & Pudlák, P. (1993). Metamathematics of First-Order Arithmetic. Berlin: Springer.CrossRefGoogle Scholar
Halbach, V. (2011). Axiomatic Theories of Truth. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Jockusch, C. G., & Soare, R. I. (1972). ${\Pi}_1^0$ classes and degrees of theories. Transactions of the American Mathematical Society , 173, 33–56.Google Scholar
Kaye, R. (1991). Models of Peano Arithmetic. Oxford Logic Guides. Oxford: Oxford University Press.CrossRefGoogle Scholar
Kossak, R., & Kotlarski, H. (1988). Results on automorphisms of recursively saturated models of PA. Fundamenta Mathematicae, 129, 9–15.CrossRefGoogle Scholar
Kossak, R., & Schmerl, J. (2006). The Structure of Models of Arithmetic. Oxford Logic Guides. Oxford: Oxford University Press.CrossRefGoogle Scholar
Kossak, R., & Wcisło, B. (2021). Disjunctions with stopping conditions. Bulletin of Symbolic Logic, 27, 231–253.CrossRefGoogle Scholar
Kotlarski, H. (1986). Bounded induction and satisfaction classes. Zeitschrift für matematische Logik und Grundlagen der Mathematik, 32, 531–544.CrossRefGoogle Scholar
Kotlarski, H., Krajewski, S., & Lachlan, A. H. (1981). Construction of satisfaction classes for nonstandard models. Canadian Mathematical Bulletin, 24, 283–293.CrossRefGoogle Scholar
Krajewski, S. (1976). Nonstandard satisfaction classes. In Marek, W., et al., editors. Set Theory and Hierarchy Theory: A Memorial Tribute to Andrzej Mostowski, 537. Berlin: Springer, pp. 121–144.CrossRefGoogle Scholar
Leigh, G. (2015). Conservativity for theories of compositional truth via cut elimination. Journal of Symbolic Logic, 80, 845–865.CrossRefGoogle Scholar
Łełyk, M. (2023). Model theory and proof theory of the global reflection principle. Journal of Symbolic Logic, 88, 738–779.CrossRefGoogle Scholar
Łełyk, M., & Wcisło, B. (2021). Local collection and end-extensions of models of compositional truth. Annals of Pure and Applied Logic, 172, Article no. 102941, 22 pp.CrossRefGoogle Scholar
Robinson, A. (1963). On languages which are based on non-standard arithmetic. Nagoya Mathematical Journal, 22, 83–117.CrossRefGoogle Scholar
Smith, S. (1987). Nonstandard characterizations of recursive saturation and resplendency. Journal of Symbolic Logic, 52, 842–863.CrossRefGoogle Scholar
Smith, S. (1989). Nonstandard definability. Annals of Pure and Applied Logic, 42, 21–43.CrossRefGoogle Scholar
Wcisło, B. (2024). Truth and collection. Preprint, arXiv:2403.19367 [math.LO].Google Scholar
Wcisło, B., & Łełyk, M. (2017). Notes on bounded induction for the compositional truth predicate. The Review of Symbolic Logic, 10, 455–480.CrossRefGoogle Scholar