No CrossRef data available.
Article contents
QUANTIFIED INTUITIONISTIC LOGIC OVER METRIZABLE SPACES
Published online by Cambridge University Press: 08 April 2019
Abstract
In the topological semantics, quantified intuitionistic logic, QH, is known to be strongly complete not only for the class of all topological spaces but also for some particular topological spaces — for example, for the irrational line, 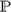 ${\Bbb P}$, and for the rational line,
${\Bbb P}$, and for the rational line, 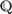 ${\Bbb Q}$, in each case with a constant countable domain for the quantifiers. Each of
${\Bbb Q}$, in each case with a constant countable domain for the quantifiers. Each of 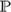 ${\Bbb P}$ and
${\Bbb P}$ and 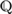 ${\Bbb Q}$ is a separable zero-dimensional dense-in-itself metrizable space. The main result of the current article generalizes these known results: QH is strongly complete for any zero-dimensional dense-in-itself metrizable space with a constant domain of cardinality ≤ the space’s weight; consequently, QH is strongly complete for any separable zero-dimensional dense-in-itself metrizable space with a constant countable domain. We also prove a result that follows from earlier work of Moerdijk: if we allow varying domains for the quantifiers, then QH is strongly complete for any dense-in-itself metrizable space with countable domains.
${\Bbb Q}$ is a separable zero-dimensional dense-in-itself metrizable space. The main result of the current article generalizes these known results: QH is strongly complete for any zero-dimensional dense-in-itself metrizable space with a constant domain of cardinality ≤ the space’s weight; consequently, QH is strongly complete for any separable zero-dimensional dense-in-itself metrizable space with a constant countable domain. We also prove a result that follows from earlier work of Moerdijk: if we allow varying domains for the quantifiers, then QH is strongly complete for any dense-in-itself metrizable space with countable domains.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2019


