Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T17:13:28.514Z Has data issue: false hasContentIssue false
  • English
  • Français

NEIGHBOURHOOD CANONICITY FOR EK, ECK, AND RELATIVES: A CONSTRUCTIVE PROOF

Published online by Cambridge University Press:  02 July 2021

FREDERIK VAN DE PUTTE  and
PAUL MCNAMARA
FREDERIK VAN DE PUTTE
Affiliation:
ERASMUS INSTITUTE FOR PHILOSOPHY AND ECONOMICS ERASMUS UNIVERSITY OF ROTTERDAM AND CENTRE FOR LOGIC AND PHILOSOPHY OF SCIENCE GHENT UNIVERSITY, GHENT, BELGIUME-mail: [email protected]
PAUL MCNAMARA
Affiliation:
PHILOSOPHY DEPARTMENT UNIVERSITY OF NEW HAMPSHIREDURHAM, NH, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

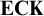We prove neighbourhood canonicity and strong completeness for the logics $\mathbf {EK}$ and $\mathbf {ECK}$ , obtained by adding axiom (K), resp. adding both (K) and (C), to the minimal modal logic 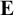$\textbf {E}$ . In contrast to an earlier proof in [10], ours is constructive. More precisely, we construct minimal characteristic models for both logics and do not rely on compactness of first order logic. The proof involves a specific circumscription technique and quite some set-theoretic maneuvers to establish that the models satisfy the appropriate frame conditions. After giving both proofs, we briefly spell out how they generalize to four stronger logics and to the extensions of the resulting six logics with a global modality.

Keywords

classical modal logicaxiom Kneighbourhood semanticscanonical completenessChellas
Type
Research Article
Information
The Review of Symbolic Logic , Volume 15 , Issue 3 , September 2022 , pp. 607 - 623
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Benton, R. A. (1975). Strong modal completeness with respect to neighborhood semantics. Unpublished manuscript. Department of Philosophy. The University of Michigan.Google Scholar
Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal Logic. Cambridge Tracts in Theoretical Computer Science, Vol. 53. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Chellas, B. (1980). Modal Logic: An Introduction. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Chellas, B. F., & Segerberg, K. (1996). Modal logics in the vicinity of S1. Notre Dame Journal of Formal Logic, 37(1), 1–24.CrossRefGoogle Scholar
Goranko, V., & Passy, S. (1992). Using the universal modality: Gains and questions. Journal of Logic and Computation, 2(1), 5–30.CrossRefGoogle Scholar
Lewis, D. (1974). Intensional logics without iterative axioms. Journal of Philosophical Logic, 3(4), 457–466.CrossRefGoogle Scholar
McNamara, P. (2019). Toward a systematization of logics for monadic and dyadic agency & ability, revisited. Filosofiska Notiser, 6, 157–188.Google Scholar
Pacuit, E. (2017). Neighbourhood Semantics for Modal Logic. Dordrecht, Netherlands: Springer.CrossRefGoogle Scholar
Surendonk, T. J. (2001). Canonicity for intensional logics with even axioms. Journal of Symbolic Logic, 66(3), 1141–1156.CrossRefGoogle Scholar
Surendonk, T. J. (1997). Canonicity for intensional logics without iterative axioms. Journal of Philosophical Logic, 26, 391–409.CrossRefGoogle Scholar