Article contents
INFINITARY TABLEAU FOR SEMANTIC TRUTH
Published online by Cambridge University Press: 08 April 2015
Abstract
We provide infinitary proof theories for three common semantic theories of truth: strong Kleene, van Fraassen supervaluation and Cantini supervaluation. The value of these systems is that they provide an easy method of proving simple facts about semantic theories. Moreover we shall show that they also give us a simpler understanding of the computational complexity of these definitions and provide a direct proof that the closure ordinal for Kripke’s definition is 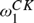 $\omega _1^{CK}$. This work can be understood as an effort to provide a proof-theoretic counterpart to Welch’s game-theoretic (Welch, 2009).
$\omega _1^{CK}$. This work can be understood as an effort to provide a proof-theoretic counterpart to Welch’s game-theoretic (Welch, 2009).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2015
References
BIBLIOGRAPHY
- 5
- Cited by


