Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-22T11:45:45.289Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITARY UPPER LOGICISM

Part of: Philosophical aspects of logic and foundations General and miscellaneous specific topics

Published online by Cambridge University Press:  31 May 2024

BRUNO JACINTO
BRUNO JACINTO*
Affiliation:
DEPARTMENT FOR THE HISTORY AND PHILOSOPHY OF SCIENCES/CENTER FOR THE PHILOSOPHY OF SCIENCES OF THE UNIVERSITY OF LISBON FACULTY OF SCIENCES CAMPO GRANDE 1749-016 LISBON PORTUGAL URL: www.brunojacinto.net
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper proposes and partially defends a novel philosophy of arithmetic—finitary upper logicism. According to it, the natural numbers are finite cardinalities—conceived of as properties of properties—and arithmetic is nothing but higher-order modal logic. Finitary upper logicism is furthermore essentially committed to the logicality of finitary plenitude, the principle according to which every finite cardinality could have been instantiated. Among other things, it is proved in the paper that second-order Peano arithmetic is interpretable, on the basis of the finite cardinalities’ conception of the natural numbers, in a weak modal type theory consisting of the modal logic 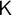$\mathsf {K}$, negative free quantified logic, a contingentist-friendly comprehension principle, and finitary plenitude. By replacing finitary plenitude for the axiom of infinity this result constitutes a significant improvement on Russell and Whitehead’s interpretation of second-order Peano arithmetic, itself based on the finite cardinalities’ conception of the natural numbers.

Keywords

logicismmodal type theoryaxiom of infinitynecessitism–contingentism debate

MSC classification

Primary: 00A30: Philosophy of mathematics
Secondary: 03A05: Philosophical and critical
Type
Research Article
Information
The Review of Symbolic Logic , Volume 17 , Issue 4 , December 2024 , pp. 1172 - 1247
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

BIBLIOGRAPHY

Adams, R. M. (1981). Actualism and thisness. Synthese, 49(1), 3–41.CrossRefGoogle Scholar
Bacon, A. (2024). Mathematical Modality: An Investigation in Higher-order Logic. Journal of Philosophical Logic, 53, 131–179.CrossRefGoogle Scholar
Balaguer, M. (1998). Non-uniqueness as a non-problem. Philosophia Mathematica, 6(1), 63–84.CrossRefGoogle Scholar
Balaguer, M. (1998). Platonism and Anti-Platonism in Mathematics. New York: Oxford University Press.CrossRefGoogle Scholar
Boolos, G. (1994). The advantages of honest toil over theft. In George, A., editor. Mathematics and Mind. Oxford: Oxford University Press, pp. 27–44.CrossRefGoogle Scholar
Bricker, P. (1991). Plenitude of possible structures. Journal of Philosophy, 88(11), 607–619.CrossRefGoogle Scholar
Bricker, P. (2020). All worlds in one: Reassessing the Forest–Armstrong argument. In Modal Matters: Essays in Metaphysics. Oxford: Oxford University Press, pp. 278–314.Google Scholar
Burgess, J. P. (1999). Which modal logic is the right one? Notre Dame Journal of Formal Logic, 40(1), 81–93.CrossRefGoogle Scholar
Button, T., & Trueman, R. (2022). Against cumulative type theory. Review of Symbolic Logic, 15(4), 907–949.CrossRefGoogle Scholar
Button, T., & Trueman, R. (2024). A fictionalist theory of universals. In Fritz, P. & Jones, N. K., editors. Higher-Order Metaphysics. Oxford: Oxford University Press.Google Scholar
Cresswell, M. J. (1965). Another basis for S4. Logique et Analyse, 8(31), 191–195.Google Scholar
Darby, G., & Watson, D. (2010). Lewis’s principle of recombination: Reply to Efird and Stoneham. Dialectica, 64(3), 435–445.CrossRefGoogle Scholar
Dedekind, R. (1888). Was Sind Und Was Sollen Die Zahlen? Brunswick: F. Vieweg.Google Scholar
Degen, W., & Johannsen, J. (2000). Cumulative higher-order logic as a foundation for set theory. Mathematical Logic Quarterly, 46(2), 147–170.3.0.CO;2-2>CrossRefGoogle Scholar
Dorr, C. (2016). To be F is to be G. Philosophical Perspectives, 30(1), 39–134.CrossRefGoogle Scholar
Dummett, M. (1993). Could there be unicorns? In The Seas of Language. Oxford: Clarendon Press, pp. 328–348.Google Scholar
Efird, D., & Stoneham, T. (2008). What is the principle of recombination? Dialectica, 62(4), 483–494.CrossRefGoogle Scholar
Felka, K. (2014). Number words and reference to numbers. Philosophical Studies, 168(1), 261–282.CrossRefGoogle Scholar
Ferrier, E. (2019). Against the iterative conception of set. Philosophical Studies, 176(10), 2681–2703.CrossRefGoogle Scholar
Field, H. (2006). Recent debates about the a priori. In Oxford Studies in Epistemology, Vol. 1. Oxford: Oxford University Press, pp. 69–88.Google Scholar
Florio, S., & Linnebo, O. (2021). The Many and the One: A Philosophical Study of Plural Logic. Oxford: Oxford University Press.CrossRefGoogle Scholar
Forrest, P., & Armstrong, D. M. (1984). An argument against David Lewis’ theory of possible worlds. Australasian Journal of Philosophy, 62(2), 164–168.CrossRefGoogle Scholar
Frege, G. (1951). On concept and object. Mind, LX(238), 168–180.CrossRefGoogle Scholar
Fritz, P. (2023). Being somehow without (possibly) being something. Mind, 132(526), 348–371.CrossRefGoogle Scholar
Fritz, P., & Goodman, J. (2016). Higher-order contingentism, part 1: Closure and generation. Journal of Philosophical Logic, 45(6), 645–695.CrossRefGoogle Scholar
Fritz, P., & Goodman, J. (2017). Counting incompossibles. Mind, 126(504), 1063–1108.CrossRefGoogle Scholar
Fritz, P., & Jones, N. K. (2024). Higher-Order Metaphysics. Oxford: Oxford University Press.CrossRefGoogle Scholar
Gallin, D. (1975). Intensional and Higher-Order Modal Logic. Amsterdam: North-Holland.Google Scholar
Geoffrey, H. (1996). Structuralism without structures. Philosophia Mathematica, 4(2), 100–123.Google Scholar
Goodsell, Z. (2021). Arithmetic is determinate. Journal of Philosophical Logic, 51(1), 127–150.CrossRefGoogle Scholar
Hellman, G. (1989). Mathematics Without Numbers: Towards a Modal-Structural Interpretation. Oxford: Oxford University Press.Google Scholar
Hodes, H. T. (1984). Logicism and the ontological commitments of arithmetic. Journal of Philosophy, 81(3), 123–149.CrossRefGoogle Scholar
Hodes, H. T. (1990). Where do the natural numbers come from? Synthese, 84(3), 347–407.CrossRefGoogle Scholar
Hofweber, T. (2005). Number determiners, numbers, and arithmetic. Philosophical Review, 114(2), 179–225.CrossRefGoogle Scholar
Hofweber, T. (2007). Innocent statements and their metaphysically loaded counterparts. Philosophers’ Imprint, 7, 1–33.Google Scholar
Hofweber, T. (2016). Ontology and the Ambitions of Metaphysics. Oxford: Oxford University Press.CrossRefGoogle Scholar
Jacinto, B. (2017). Strongly Millian second-order modal logics. Review of Symbolic Logic, 3, 1–58.Google Scholar
Jacinto, B. (2019). Serious actualism and higher-order predication. Journal of Philosophical Logic, 48(3), 471–499.CrossRefGoogle Scholar
Jones, N. K. (2018). Nominalist realism. Noûs, 52(4), 808–835.CrossRefGoogle Scholar
Jones, N. K., & Florio, S. (2021). Unrestricted quantification and the structure of type theory. Philosophy and Phenomenological Research, 102(1), 44–64.Google Scholar
Krämer, S. (2017). Everything, and then some. Mind, 126(502), 499–528.Google Scholar
Lambert, K. (1962). Notes on e! III: A theory of descriptions. Philosophical Studies, 13(4), 51–59.CrossRefGoogle Scholar
Lewis, D. (1986). On the Plurality of Worlds. Oxford: Wiley-Blackwell.Google Scholar
Linnebo, O. (2018). Thin Objects: An Abstractionist Account. Oxford: Oxford University Press.CrossRefGoogle Scholar
Linnebo, O., & Rayo, A. (2012). Hierarchies ontological and ideological. Mind, 121(482), 269–308.CrossRefGoogle Scholar
Linnebo, O., & Shapiro, S. (2019). Actual and potential infinity. Noûs, 53(1), 160–191.CrossRefGoogle Scholar
MacBride, F. (2008). Predicate reference. In Smith, B. C., editor. The Oxford Handbook of Philosophy of Language. Oxford: Oxford University Press, pp. 422–475.Google Scholar
MacFarlane, J. (2000). What Does It Mean to Say that Logic Is Formal? Ph.D. Thesis. University of Pittsburgh.Google Scholar
Moltmann, F. (2013). Reference to numbers in natural language. Philosophical Studies, 162(3), 499–536.CrossRefGoogle Scholar
Nolan, D. (1996). Recombination unbound. Philosophical Studies, 84(2–3), 239–262.CrossRefGoogle Scholar
Novaes, C. D. (2014). The undergeneration of permutation invariance as a criterion for logicality. Erkenntnis, 79(1), 81–97.CrossRefGoogle Scholar
Panza, M., & Sereni, A. (2019). Frege’s constraint and the nature of Frege’s foundational program. Review of Symbolic Logic, 12(1), 97–143.CrossRefGoogle Scholar
Plantinga, A. (1976). Actualism and possible worlds. Theoria, 42(1–3), 139–160.CrossRefGoogle Scholar
Prior, A. N. (1957). Time and Modality. Oxford: Clarendon Press.Google Scholar
Prior, A. N. (1971). Objects of Thought. Oxford: Clarendon Press.CrossRefGoogle Scholar
Pruss, A. R. (2001). The cardinality objection to David Lewis’s modal realism. Philosophical Studies, 104(2), 169–178.CrossRefGoogle Scholar
Rayo, A. (2013). The Construction of Logical Space. Oxford: Oxford University Press.CrossRefGoogle Scholar
Rayo, A. (2021). Beta-conversion and the being constraint. Aristotelian Society Supplementary, 95(1), 253–286.CrossRefGoogle Scholar
Rayo, A., & Yablo, S. (2001). Nominalism through de-nominalization. Noûs, 35(1), 74–92.CrossRefGoogle Scholar
Roeper, P. (2016). A vindication of logicism. Philosophia Mathematica, 24(3), 360–378.CrossRefGoogle Scholar
Russell, B. (1919). Introduction to Mathematical Philosophy. London: Allen and Unwin.Google Scholar
Salmon, N. (1989). The logic of what might have been. Philosophical Review, 98(1), 3–34.CrossRefGoogle Scholar
Shapiro, S. (1991). Foundations Without Foundationalism: A Case for Second-Order Logic. New York: Oxford University Press.Google Scholar
Shapiro, S. (1998). Logical consequence: Models and modality. In Schirn, M., editor. The Philosophy of Mathematics Today. Oxford: Clarendon Press, pp. 131–156.CrossRefGoogle Scholar
Shapiro, S. (2005). Logical consequence, proof theory, and model theory. In Shapiro, S., editor. Oxford Handbook of Philosophy of Mathematics and Logic. Oxford: Oxford University Press, pp. 651–670.CrossRefGoogle Scholar
Sher, G. (1991). The Bounds of Logic: A Generalized Viewpoint. Cambridge: MIT Press.Google Scholar
Skiba, L. (2021). Higher-order metaphysics. Philosophy Compass, 16(10), 1–11.CrossRefGoogle Scholar
Skiba, L. (2021). Higher-order metaphysics and the tropes versus universals dispute. Philosophical Studies, 178, 2805–2827.CrossRefGoogle Scholar
Stafford, W. (2023). The potential in Frege’s theorem. Review of Symbolic Logic, 16(2), 553–577.CrossRefGoogle Scholar
Stalnaker, R. (1984). Inquiry. Cambridge: Cambridge University Press.Google Scholar
Stalnaker, R. (1994). The interaction of modality with quantification and identity. In Sinnott-Armstrong, W., editor. Modality, Morality and Belief. Essays in Honor of Ruth Barcan Marcus. Cambridge: Cambridge University Press, pp. 12–28.Google Scholar
Stalnaker, R. (2012). Mere Possibilities: Metaphysical Foundations of Modal Semantics. Princeton: Princeton University Press.Google Scholar
Stalnaker, R. (2016). Models and reality. Canadian Journal of Philosophy, 46(4–5), 709–726.CrossRefGoogle Scholar
Stalnaker, R. (2022). Propositions: Ontology and Logic. New York: Oxford University Press.Google Scholar
Studd, J. P. (2023). Linnebo’s abstractionism and the bad company problem. Theoria, 89(3), 366–392.CrossRefGoogle Scholar
Suszko, R. (1975). Abolition of the Fregean axiom. Lecture Notes in Mathematics, 453, 169–239.CrossRefGoogle Scholar
Tarski, A. (1986). What are logical notions? History and Philosophy of Logic, 7(2), 143–154.CrossRefGoogle Scholar
Tennant, N. (2023). Logicism and neologicism. In Zalta, E. N. & Nodelman, U. editors, Stanford Encyclopedia of Philosophy https://plato.stanford.edu/archives/win2023/entries/logicism/.Google Scholar
Trueman, R. (2021). Properties and Propositions: The Metaphysics of Higher-Order Logic. Cambridge: Cambridge University Press.Google Scholar
Whitehead, A. N., & Russell, B. (1910). Principia Mathematica. Cambridge: Cambridge University Press.Google Scholar
Williamson, T. (2013). Modal Logic as Metaphysics. Oxford: Oxford University Press.CrossRefGoogle Scholar
Woods, J. (2016). Characterizing invariance. Ergo: An Open Access Journal of Philosophy, 3, 778–807.Google Scholar
Wright, C. (2000). Neo-Fregean foundations for real analysis: Some reflections on Frege’s constraint. Notre Dame Journal of Formal Logic, 41(4), 317–334.CrossRefGoogle Scholar
Wright, C. (2007). On quantifying into predicate position: Steps towards a new (tralist) perspective. In Leng, M., Paseau, A. & Potter, M., editors. Mathematical Knowledge. Oxford: Oxford University Press, pp. 150–174.CrossRefGoogle Scholar